采用格基规约算法的空间调制检测方案

张文彬，王 孝，陶臣嵩，何晨光

（哈尔滨工业大学通信技术研究所，150080哈尔滨）

采用格基规约算法的空间调制检测方案

张文彬，王 孝，陶臣嵩，何晨光

（哈尔滨工业大学通信技术研究所，150080哈尔滨）

空间调制是未来5G蜂窝通信系统的物理层备选技术之一，为研究LLL、嵌入式两种格基规约算法对空间调制技术的影响，设计了两种检测方案，分别为LLL辅助MMSE检测方案和嵌入式检测方案.在不同的调制符号、不同的天线数目下，通过仿真比较两种检测方案的误比特率性能.然后通过矩阵运算理论对两种检测方案的运算复杂度进行分析，为使分析结果更直观，在不同天线数目下，对两种方案的运算复杂度进行了仿真.理论分析和仿真结果表明，嵌入式检测方案在误比特率和运算复杂度两方面均优于LLL辅助MMSE检测方案，它更适用于空间调制技术.

空间调制；格基规约；LLL算法；嵌入式算法

近些年出现的空间调制技术SM（spatial modulation）可看做大规模MIMO系统的一个特例.它利用发射端天线的序号组合携带部分信息，可降低功耗及发射机的复杂度［1-2］.空间调制与空间多路MIMO系统的差别在于空间调制多了一个天线序号的检测环节.目前空间多路MIMO系统的检测算法包括：最大似然算法（ML）、迫零算法（ZF）、最小均方误差算法（MMSE）等［3］，后两者属于线性检测算法，运算复杂度较低，但误比特性能较差.误比特性能较差的根源在于MIMO信道矩阵的各列是非正交的，针对这一问题，有学者采用格基规约来改善空间多路MIMO中信道矩阵各列的正交性［4-6］.但目前还没有文献研究格基规约算法对空间调制技术的影响，本文尝试做一些这方面的研究工作.

多种格基规约算法中，LLL（lenstra-lenstralovasz）算法是最常用的经典算法［7］，Augmented lattice reduction（嵌入式算法）［8-10］是近些年出现的算法，本文以这两种算法为基础，设计了两种空间调制技术检测方案：LLL辅助MMSE方案和嵌入式方案.通过理论分析和仿真研究了两种方案的误比特性能和运算复杂度，所得结果表明嵌入式方案优于LLL辅助MMSE方案.

1 空间调制模型

图1所示是一个采用空间调制技术的nT×nRMIMO系统，其数学模型为

式中发射信号向量为x=［x1，x2，…，xnT］T，对于空间调制技术，由于只有部分天线发射信号，可把不发射信号的分量置为“0”，例如，如果第1号天线和第2号天线发送符号，其余天线不发送符号，则发射信号向量为x=［x1，x2，0…，0］T；接收信号向量为y=［y1，y2，…，ynR］T；信道矩阵Hbasic为nR×nT矩阵；接收端接收到的噪声为n=［n1，n2，…，nnR］T，每个噪声分量的均值为0，方差为σ2n．

图1 空间调制技术

LLL算法一般针对实数进行处理，而式（1）中的各量都为复数，因此需要对其实数化，信道矩阵的实数化过程：

实数化发射向量¯x=［Re（xT），Im（xT）］T∈R2nT，类似得到¯y=［Re（yT），Im（yT）］∈R2nR．对信道矩阵H和接收信号矢量¯y进行扩展得

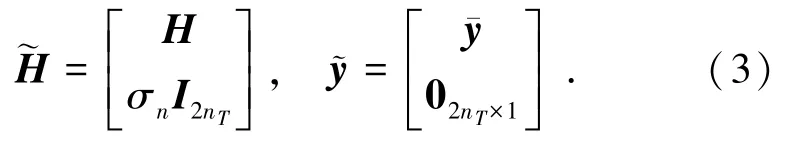
2 两种格基规约检测方案

2.1 LLL辅助MMSE检测方案

LLL辅助MMSE检测方案，以后简称LLL+ MMSE方案，它由LLL+MMSE算法［11］和空间调制信号的检测两部分组成.先介绍LLL+MMSE算法，通过式（3）可将MMSE转化成ZF的形式［12］，转化后的算法执行过程见图2.利用LLL算法对式（3）中的˜H进行格基规约，得

式中：T为幺模矩阵，矩阵中的元素均为整数，且行列式的值为±1；其初始取值为单位矩阵I，而后在格基规约的具体处理过程中因˜H而异．针对˜Hred，˜y，采用式（5）中的迫零算法求出zLLL+MMSE．

利用量化器及幺模矩阵得

空间调制信号的检测见图3，将式（6）中得到的2nT维向量＾xLLL+MMSE作为待检测量，对其2nT个分量按绝对值从大到小排序，假设空间调制激活m根天线发射信号，就挑选排序表中前m个分量，通过对m个分量的序号进行加nT（如果分量序号≤nT）或者减nT（如果分量序号＞nT）的操作，确定另外m个分量，然后根据这2m个分量确定发射端采用的天线序号组合，接下来对天线序号组合对应的各分量进行最大似然检测以确定各根天线上发送的调制符号，最后根据空间调制映射表，找到与天线序号组合、各根天线上的调制符号相对应的一组比特，完成空间调制信号的检测．

图2 LLL+MMSE算法的执行过程

图3 空间调制信号的检测

2.2 嵌入式检测方案

嵌入式检测方案，简称Aug方案，是由嵌入式算法（简称Aug算法）和空间调制信号的检测两部分组成.Aug算法［8］见图4，对式（3）中的信道矩阵˜H进行扩展得到（2nR+2nT+1）×（2nT+1）维的扩展信道矩阵

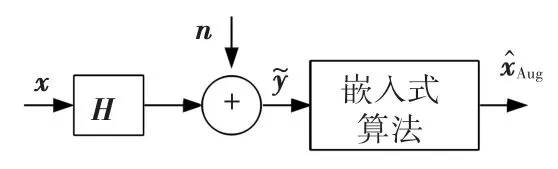
图4 Aug算法的执行过程

利用LLL算法对矩阵˜H进行格基规约

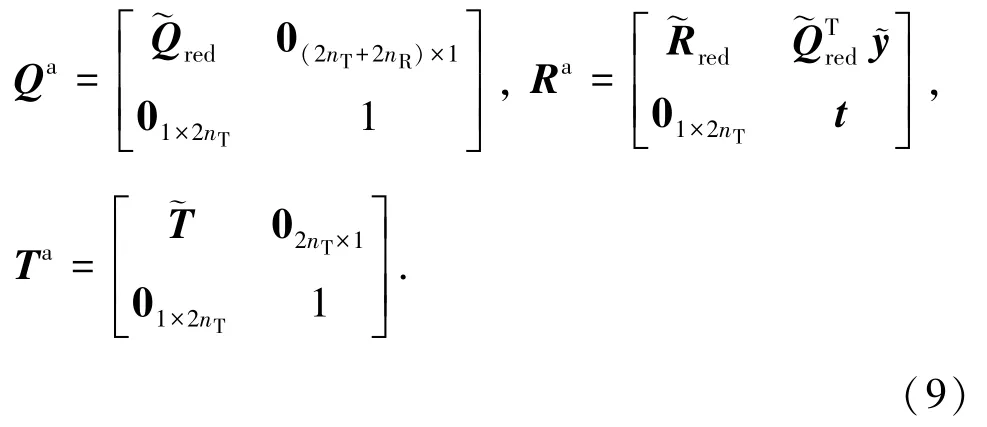
其中t为待定系数，由上述各扩展矩阵的形式可知HaTa=QaRa，而QaRa中除最后一列外都满足LLL格基规约条件，因此只需用LLL算法格基规约HaTa的最后一列，所得矩阵为

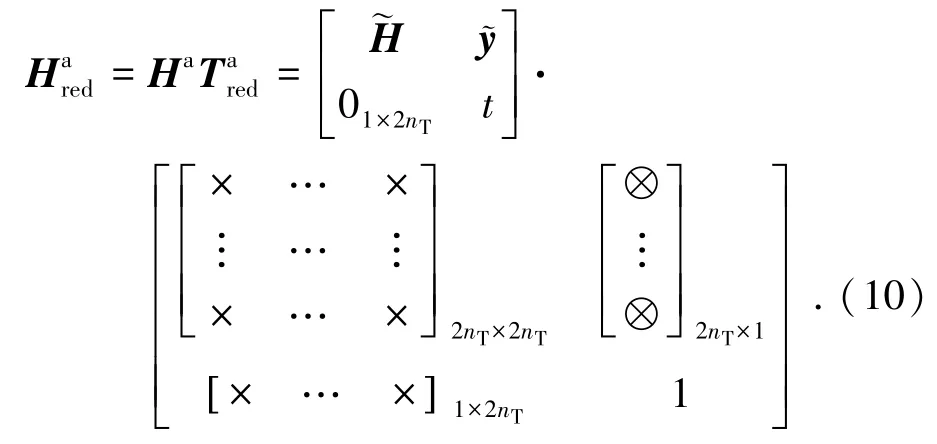
当所选参数t＞˜Rred（2nT，2nT）时，根据格基规约的特性可知：格基规约基中的每个向量的长度都接近于由格基张成的格中的最短格点的长度，因此矩阵中的最后一列⊗元素的相反数对应于在2范数下的的最小整数二乘解．解记为，然后将作为待检测量代入图3所示过程，完成了空间调制信号的检测，对比上述两种检测方案可发现：两种检测方案的最后一个环节是相同的，它们都是采用图3所示的过程进行空间调制信号的检测.在此之前的处理过程是不同的，LLL+MMSE算法是LLL算法和MMSE算法的结合，它先利用LLL算法得到正交性较好的信道矩阵，在此基础上利用MMSE算法进行信号检测，由此可见，此算法主要利用了格基规约提高信道矩阵各列之间正交性的效果.Aug算法是扩展信道矩阵和LLL算法的结合，它先对信道矩阵及其相关矩阵进行扩展，再利用LLL算法对扩展信道矩阵进行规约，进而得到待检测信号，Aug算法中没有涉及MMSE算法.

3 误比特率仿真分析

3.1 仿真设置及说明

发射端调制方式包括：空间多路BPSK调制、QPSK+SM、16QAM+SM；接收端检测算法包括：LLL+ MMSE算法、Aug算法和ML算法.为实现比较的公平性，不同的调制方式采用相同的信道接入速率.仿真中的信道矩阵元素服从（0，1）复高斯分布.

仿真不考虑比特信息的编码／译码过程，就数字信号的各种调制方式而言，均使用标准的星座图进行映射，且每个BPSK符号需要1 bit的0／1信息、每个QPSK符号需要2 bit的0／1信息、每个16QAM符号需要4 bit的0／1信息.“信道接入速率”的单位为“bit／信道接入”，表示单位时间内发射端发送至信道的0／1信息比特数，此单位时间可以是“1秒”，也可以是“1微秒”等.

3.2 误比特率仿真

1）信道接入速率为5 bit／信道接入的5×8系统.在单位时间内有5bit的0／1信息需要发射端发送至信道，发射端分别采用空间多路BPSK调制和QPSK+SM调制方式.其中空间多路BPSK使用5根发射天线同时发射5路BPSK符号；QPSK+SM的实现方法是将5 bit分成3、2 bit两部分，其中的3 bit用于从5根发射天线中选2根发射天线，2 bit用于确定1个QPSK符号，2根激活天线发射相同的QPSK符号，具体方案见表1.在两种调制方式下，接收端分别使用LLL+MMSE、Aug和ML3种检测算法.

表1 5天线选2天线且发射相同QPSK符号的映射表

仿真结果见图5，此图反映出：当发射端采用低阶调制BPSK或QPSK时，采用Aug算法对空间调制信号进行检测可取得较好的误比特性能，其性能接近于“发射端采用空间多路BPSK，接收端使用ML算法”的情况.而在发射端使用相同调制方式的情况下，3种检测算法的误比特性能表现为：ML算法优于Aug算法，Aug算法优于LLL+MMSE算法.

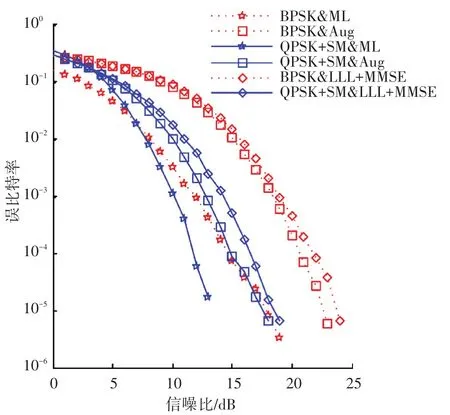
图5 5×8系统，BPSK／QPSK+SM，LLL+MMSE／Aug／M L的误比特率

2）信道接入速率为10 bit／信道接入的5×8系统.在单位时间内有10 bit的0／1信息需要发射端发送至信道，发射端分别采用空间多路QPSK和16QAM+SM调制方式.其中的空间多路QPSK使用5根发射天线同时发送5路QPSK符号；在16QAM+ SM调制方式中，10个bit中的2个bit用于从5根发射天线中选2根天线，其余8个bit用于选择两个不同的16QAM调制符号，具体方案见表2.在两种调制方式下，接收端分别使用LLL+MMSE、Aug和ML3种检测算法.

表2 5天线选2天线且发送不同16QAM的映射表

由于运算复杂度过大，没有对16QAM+SM的ML检测进行仿真.仿真结果见图6，此图反映出：在接收端采用相同的检测算法条件下，发射端采用高阶调制方式产生的误比特率要高于用低阶调制方式产生的误比特率.但是无论在哪一种调制方式下，Aug算法的误比特性能均优于LLL+MMSE算法.

3）信道接入速率为10 bit／信道接入的10×10系统.在单位时间内有10 bit的0／1信息需要发射端发送至信道，发射端分别采用空间多路BPSK和QPSK+ SM调制方式.其中的空间多路BPSK使用10根发射天线同时发送10路信号；在QPSK+SM调制方式中，10个bit中的4个bit用于从10根发射天线中选3根天线，其余6个bit对应于3根发射天线上的3个不同的QPSK符号，具体方案见表3.在两种调制方式下，接收端分别采用LLL+MMSE、Aug和ML3种检测算法.

图6 5×8系统，QPSK／16QAM+SM，LLL+MMSE／Aug／M L的误比特率

表3 10天线选3天线且发射不同QPSK符号的映射表

由于运算复杂度过大，没有对QPSK+SM的ML检测进行仿真.仿真结果如图7所示，此图反映出：无论在空间多路情况下，还是在空间调制下，Aug算法的误比特性能都优于LLL+MMSE算法，特别是在空间调制下，Aug算法的性能大大优于LLL+MMSE算法.

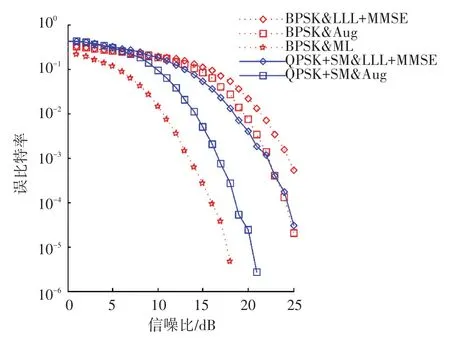
图7 10×10系统，BPSK／QPSK+SM，LLL+MMSE／Aug／M L的误比特率

4 运算复杂度理论分析及仿真

4.1 仿真设置

nT为发射天线总数，n=2nT；nR为接收天线总数；信道矩阵Hbasic为nR×nT维复矩阵；发射信号向量x为nT×1维复向量；接收信号向量y为nR×1维复向量．算法运算复杂度的指标为算法包括的实数乘法、除法及开方的次数总和．

4.2 运算复杂度理论分析

两种空间调制检测方案的不同之处在于：一个采用Aug算法，另一个采用LLL+MMSE算法.考虑到采用排序的奇异值分解（SQRD）可以减小LLL算法的复杂度，本文将图4中的Aug算法执行过程转变成了图8所示的形式，二者主要的差别在于图8多了一个置换矩阵P，这个矩阵是在利用排序的奇异值分解对式（3）中的进行LLL格基规约时产生的置换矩阵，用替换之后，从到的处理过程同图3描述的嵌入式算法的处理过程一致了．消除置换矩阵P的影响，执行

采用排序的奇异值分解对图2所示的LLL+ MMSE算法执行过程进行处理得到图9所示的形式.

图8 采用排序的奇异值分解的Aug算法执行过程

1）嵌入式方案的复杂度

①利用式（2）对信道矩阵Hbasic进行复数到实数的变换，得到H矩阵，其维度变为2nR×2nT；

图9 采用排序的奇异值分解的LLL+MMSE算法执行过程

②根据式（3），对实数信道矩阵H进行扩展，得到˜H，其维度变为（2nR+2nT）×2nT；

④扩展得到矩阵Ha时用到了，运算复杂度增加了n×n×（n+2nR），扩展得到矩阵Ra时由式（9）可知运算复杂度增加了n×（n+2nR）；

⑤对扩展矩阵Ha最后一列进行简化LLL处理的循环过程中，运算复杂度增加

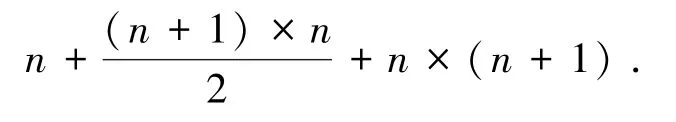
⑥对所得到的检测结果进行置换矩阵P的还原时运算复杂度增加了n×n；

⑦对＾xAug执行如图3所示的空间调制信号的检测过程时，运算复杂度增加了counter3.

综上所述，利用嵌入式检测方案对空间调制发射信号向量进行一次检测所需的运算复杂度为

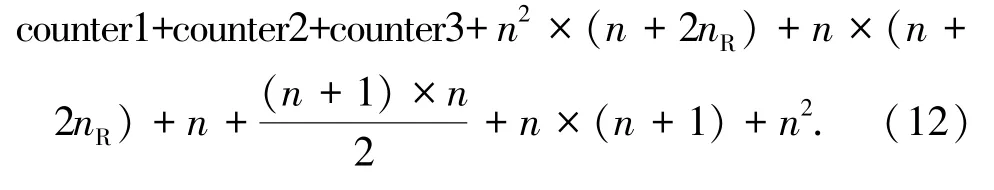
2）LLL辅助MMSE方案的复杂度

①处理过程同1）嵌入式方案的复杂度中的①、②、③相同，运算复杂度增加了counter1和counter2；

②LLL格基规约处理之后的信道矩阵为Hred，而在得到它的过程之中，由于运算复杂度增加了2×n×n×（n+2nR）；

③求矩阵Hred的MP逆时运算复杂度增加了6×n×n×n+4×nR×n×n；

④将矩阵Hred的MP逆与经过扩展的接收信号向量˜y相乘时运算复杂度增加了n×（n+2nR）；

⑤对所得到的检测结果进行置换矩阵P和幺模矩阵T的还原时运算复杂度增加了：n×n+n×n；

⑥对＾xLLL+MMSE执行见图3所示的空间调制信号的检测过程，运算复杂度增加了counter3.

综上所述，利用LLL辅助MMSE检测方案对空间调制发射信号向量进行一次检测所需的运算复杂度为

4.3 运算复杂度仿真

式（12）、（13）中的counter1、counter2、counter3是相等的，因此只对两个公式中其余项进行仿真。收发天线数目相同、不同的仿真结果分别如图10、11所示.可以看出：在任何天线配置下，Aug检测方案的复杂度都低于LLL+MMSE检测方案的复杂度，而且随着天线数目的增加，二者的差距逐渐增大.

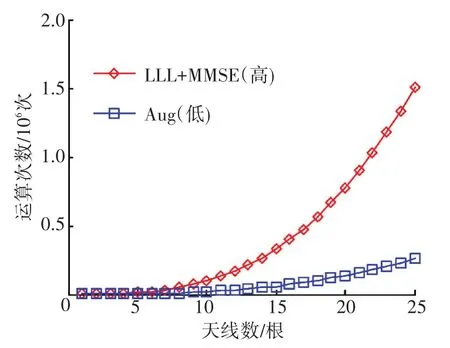
图10 发、收天线数相同时算法复杂度比较

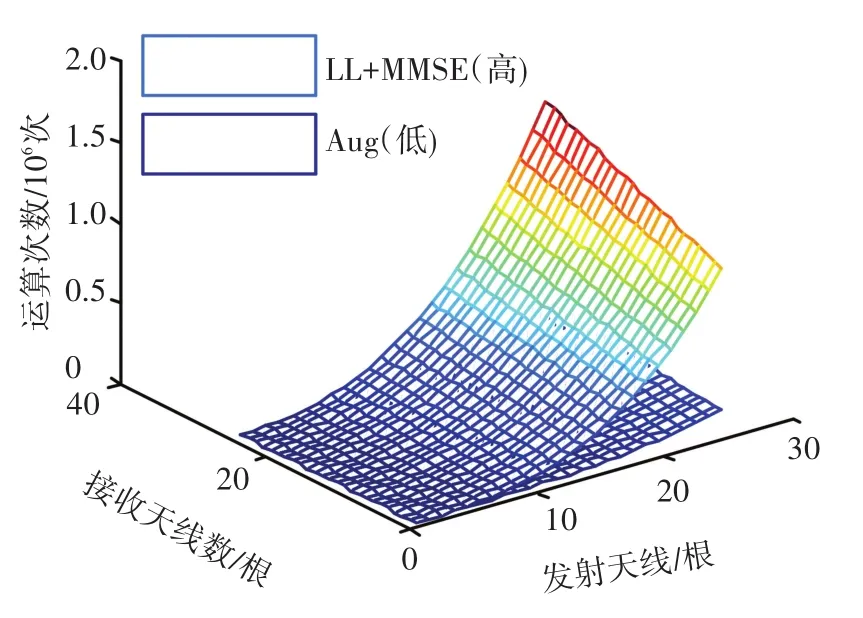
图11 发、收天线数不同时算法复杂度比较

5 结 语

为研究格基规约算法对空间调制技术的影响，设计了基于Aug算法和LLL+MMSE算法的空间调制技术检测方案.在不同的调制符号、信道接入速率、激活天线数目下对两种检测方案的误比特率性能进行了仿真，仿真结果表明Aug检测方案优于LLL+MMSE检测方案.考虑到运算复杂度是衡量检测算法优劣的重要指标，对两种检测算法的运算复杂度进行了详细的理论分析和仿真，所得结果表明：无论是在收发天线数目相同还是不同的情况下，Aug检测方案的运算复杂度都低于LLL+MMSE检测方案，而且随着天线数目的增加，二者的差距拉大.综合误比特率和运算复杂度两项指标，可以得出结论：Aug检测方案更加适用于空间调制技术.

［1］MEN Hongzhi，JIN Minglu.A low-complexity ML detection algorithm for spatial modulation systems with MPSK constellation［J］.IEEE Communications Letters，2014，18（8）：1375-1378.

［2］曲倩倩，郑剑锋，陈为刚，等.结合天线选择的空间调制及性能仿真［J］.计算机工程与应用，2012，48（17）：99-104.

［3］YONG Soocho，KIM J，WON Youngyang，et al.MIMOOFDM Wireless Communications with MATLAB［M］. Singapore：IEEE PRESS，2010：319-373.

［4］WUBBEN D，SEETHALER D，JALDEN J，et al.Lattice reduction—a survey with applications in wireless communications［J］.IEEE Signal Processing Magazine，2011，28（3）：70-91.

［5］YAO H，WORNELL，GREGORY W.Lattice-reductionaided detectors for MIMO communication systems［C］／／Global Telecommunications Conference 2002.Taipei：IEEE，2002：424-428.

［6］WUBBEN D，BOHNKE R，KUHN V，et al.Nearmaximum likelihood detection of MIMO systems using MMSE based lattice reduction［C］／／IEEE International Conference on Communications 2004.Paris：IEEE，2004：798-802.

［7］PHONG Q，NGUYEN，BRIGITTE V.The LLL Algorithm-Survey and Applications［M］.Berlin Heidelberg：Springer，2009：145-179.

［8］KIM N，HYUNCHEOL P.Improved lattice reduction aided detections for MIMO systems［C］／／2006 IEEE 64th Vehicular Technology Conference.Montreal：IEEE，2006：1-5.

［9］LUZZI L，OTHMAN G R，BELFIORE J.Augmented lattice reduction for MIMO decoding［J］.IEEE Transactions on Wireless Communications，2010，9（9）：2853-2859.

［10］LUZZIL，STEHLED，CONG L.Decoding by embedding：correct decoding radius and DMT optimality［J］.IEEE Transactions on Information Theory，2013，59（5）：2960-2973.

［11］郭腾，林云.MIMO系统中信号检测算法的研究［J］.现代电信科技，2010，25（11）：48-51.

［12］WUBBEN D，BOHNKE D，KUHN V，et al.MMSE-based lattice-reduction for near-ML detection of MIMO systems［C］／／2004 ITG Workshop on Smart Antennas.Munich：IEEE，2004：106-113.

（编辑苗秀芝）

Spatialmodulation detection schemes based on lattice reduction algorithm

ZHANGWenbin，WANG Xiao，TAO Chensong，HE Chenguang
（Communication Research Center，Harbin Institute of Technology，150080 Harbin，China）

Spatialmodulation is one of the alternative physical layer technologies in 5G cellular communication system.To study the influence of LLL algorithm and augmented lattice reduction on the bit error rate and computational complexity of spatial modulation，two schemes are proposed，which are called LLL aided MMSE detection scheme and augment detection scheme.With differentmodulation symbols and different antenna numbers，the error rate of the two detection schemes is compared by simulation.Then，the computational complexity of the two detection schemes is compared by thematrix operation analysis.Tomake the analysis resultmore intuitive，the simulation with different antenna numbers is executed.Theoretical analysis and simulation results show that in the aspect of bit error rate and computational complexity，the augment detection scheme excels the LLL aided MMSE detection scheme.Therefore，the augment detection scheme ismore suitable for spatialmodulation technology.

spatialmodulation；lattice reduction；LLL algorithm；augmented lattice reduction

TN911.3

：A

：0367-6234（2015）11-0063-06

10.11918／j.issn.0367-6234.2015.11.011

2015-07-29.

黑龙江省科学基金项目（F2015001）；中央高校基本科研业务费专项资金资助（HIT.NSRIF.2012019）.

张文彬（1973—），男，副教授，硕士生导师.

张文彬，zwbgxy1973＠hit.edu.cn.