基于能量分配提高纠错码误比特率性能的研究

张卫党，李 萍

(郑州大学信息工程学院，河南郑州450001)

0 引言

随着数字通信系统的飞速发展，每天都在不断涌现出新的通信业务和信息业务，同时用户对通信质量和数据传输速率的要求也在不断提高，这就促使我们尽可能地解决数字通信中始终存在的可靠性和有效性的矛盾.纠错码是为通信系统中可靠性提供保障的一种手段，所以如何研究并利用好纠错码技术已成为一项重要任务，而衡量一种纠错码技术好坏的主要标准是误比特率性能.因此，针对如何提高各种纠错码的误比特率性能一直是纠错码的研究热点.为了达到这个目的已经有很多方案被提出，且这些方案被证实在一定程度上对码字的误比特率性能有所提高.一种方法是通过改变编译码的结构和算法来改进当前性能较好的纠错码，已经有大量的文献采用这些方法［1-3］.还有一种方法是通过能量分配来提高码字的误比特率性能，这种方法基本上不会影响到码字的编译码结构和算法，所以使用时方便简单，已有一些文献在这一方面做了研究.例如Mohammadi等［4］提出了一种不等能量分配方案，该方案针对传统能量分配方案中信息位和校验位被分配同等的能量不能使Turbo码的性能得到改善的问题，通过对信息位和校验位分配不同的能量来提高码字的性能，其中两分量码输出的校验信息分配的能量是相同的.而文献［5］作者针对非对称Turbo码对上述能量分配方案进行改进，为两分量码输出的校验位也分配不等的能量，在文献［6］中作者通过对Turbo码低重量码字分配较多的能量来降低其“错误平层”.基于以上研究，笔者提出一种新的能量分配方案，该方案仍然是基于低重量码字分布，但它考虑到了所有的低重量码字得到了与码字序列中每一位比特相连的最轻码字和它们数目，然后利用文献［7］推导出的估计信息位误比特率分布的计算公式，对码字进行按位能量分配，通过仿真结果得出该方案不仅不会增加系统的复杂度，它还可以改善多种纠错码的误比特率性能，具有实现简单、应用范围广等优点.

1 一致界和误比特率分布公式

文献［7］中给出了在AWGN信道下，误比特率由下式给出上限:

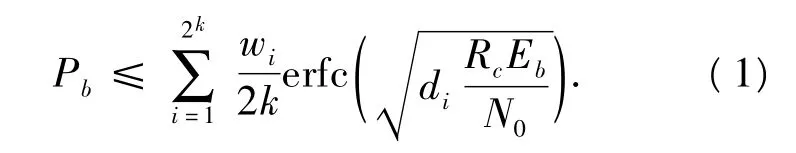
式中:wi，di分别为第i个码字的信息部分的重量和总重量;k为输入序列的长度;Rc为编码速率;Eb为码字中每比特信息的能量;N0为噪声的功率谱密度.而且在文献［7］中作者根据公式(1)推导出了一个估计误比特率分布的理论公式，该公式只考虑与码字中每个比特位相连的重量最轻的码字，由下式给出:

式中:dmin(j)为与第j位信息位相连的最轻码字的重量;nmin(j)为这个重量的码字的数目，j=1，2，…，N-1，其中N为码字的长度.

一般情况下，对码字中的每一比特位Eb都是一个常数，这种传统能量分配方案不能使码字的性能得到改善.为了降低码字的平均误比特率，笔者将根据公式(2)推导出一种不等能量分配方案，对码字中每一比特位进行重新分配.

2 优化能量分配方案

由于码字本身所具有的不等差错保护能力，码字中每一比特位上的误比特率不可能是一个常数，特别是在高信噪比时，码字的平均误比特率主要是由误比特率较高的位置所决定的，在码字的总能量保持不变的前提下，由公式(2)可以看出当为误比特率较高的位置分配较多的能量以降低这些位置的误比特率时，另外一些位置的误比特率就会增加.从公式(2)可以看出，如果信息的某个比特位与较轻重量的码字相连，这个比特位的纠错能力就较弱，误比特率就会较高，为这些位置分配较多的能量，不断重复这个过程，直到Pb(j)对于j=1，2，…，N-1(N为码字的长度)为一个常数.将该能量分配方案应用于公式(2)中得到下式:

由式(3)可以得出:

在码字的总能量不变的前提下如式:

由式(4)和式(5)可以得到:

从以上式子中可以看出，如果可以找出与每比特位相连的最轻码字的重量dmin(j)和这个重量的码字数目nmin(j)，就可以通过公式(6)得到所要求的，再由式(4)即可计算出分配给每比特位的能量Eb(j)，然后将该能量分配方案应用于不同类型的纠错码中检验其效果.

3 仿真结果与分析

为了清楚地显示该方案的有效性和解释运用该方案使平均误比特率降低的原因，下面首先将其运用到一个简单的(15，4)线性分组码，该码字的生成矩阵为

可以很容易地找出该码字中每一比特位的码重分布，从而得到每比特位相连的最轻码字的重量dmin(j) 分别为 7，5，7，5，4，8，5，4，5，4，7，8，7，5，4，这些重量的码字数目 nmin(j) 分别为 2，1，2，1，1，4，1，1，1，1，2，4，2，1，1.从式(2) 可以看出第 4，7，9 和14位比其它比特位更容易受到噪声的影响从而产生误码，所以为了得到较低的平均误比特率，为这些位置分配较多的能量.由式(4)和(6)，表1给出了一些信噪比下每比特位的能量分配Eb(j).

表1 不同信噪比下的优化能量分配Eb(j)Tab.1 The optimized energy allocations Eb(j)at different SNR

从表1可以清楚地看出在低信噪比(如0 dB)和高信噪比(如12 dB)时，Eb(j)的分布有很大的不同，在高信噪比时，每比特位的能量Eb(j)的分布与该位相连的最轻码字的重量dmin(j)有紧密的联系，dmin(j)越小，Eb(j)越大，而在低信噪比时，这种关系不明显.这是因为在低信噪比时不只是取决于dmin(j)和nmin(j)，它还和其他码重分布有关，而在高信噪比时，平均误比特率基本由dmin(j)和nmin(j)决定，且dmin(j)在公式中是指数的形式，对影响较大，故Eb(j)的分布主要由dmin(j)决定，如在第4，7，9和14位，dmin(j) 都为4，是码字中dmin(j)最小的一些位置，比较容易产生误码，所以在高信噪比时，这些位置分配的Eb(j)是最多的，例如在SNR=12 dB时都为1.32，由式(6)也可知在不同的信噪比下，Eb(j)也是不同的.

图1中给出了4条曲线，它们应用上文中给出的dmin(j)和nmin(j)，分别由式(2)、式(6)和仿真结果产生.图2给出了在信噪比SNR=5 dB时由仿真得到的两条位误比特率的曲线.

图1 (15，4)线性分组码优化能量分配前后平均误比特率理论和仿真曲线Fig.1 The theoretic BER curves and simulation BER curves before and after optimizing for a(15，4)linear code

由图1可以看出能量分配后的所有平均误比特率曲线都要低于能量分配之前的曲线，特别是在高信噪比时，这种现象更加明显.例如在SNR=8 dB时，能量分配后的理论和仿真曲线分别比能量分配前的理论和仿真曲线改善了约一个数量级，在SNR=12 dB时，能量分配后的理论值比能量分配前的理论值低了多于一个数量级.而图2显示出码字在能量分配之后其位误比特率曲线比能量分配前的曲线平滑，原本位误比特率较高的位置能量分配后误比特率得到了降低，而原本位误比特率较低的位置，相应的位误比特率增加了，整个曲线得到了较能量分配前平均的结果.这两个图都表明该能量分配方案对线性分组码是有效的，特别是在高信噪比时，其作用更明显.

为了验证改方案不只是适用于一种特定类型的纠错码，下面将该能量分配方案应用于另外一种纠错码-卷积码并给出其仿真结果.图3和图4都给出了四条曲线，其产生方法与图1相同，所用的卷积码为(2，1)卷积码，其生成矩阵 g=(171，133)，输入码字长度为32，但图3所用的卷积码为不结尾卷积码，而图4所用卷积码为结尾卷积码.

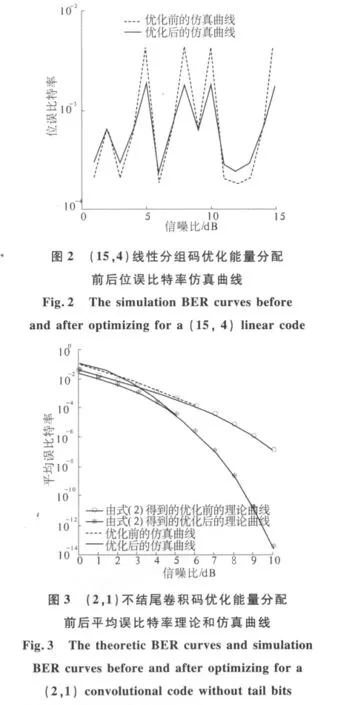
图3给出了与图1相似的结果，例如在SNR=6 dB时，能量分配后的仿真曲线分别比能量分配前的仿真曲线改善了约两个数量级，在SNR=10 dB时，能量分配后的理论值比能量分配前的理论值低了多于七个数量级.但是值得注意的是，在低信噪比时，能量分配后的系统误比特率性能还没有能量分配前的好，这是因为公式(2)给出的误比特率估算公式在低信噪比时估算不精确，从而导致该能量分配方案达不到预期的效果，而在高信噪比时该公式和方案都有很好的效果.从图1和图3可以得出该方案不只是使用于一种特定类型的纠错码.

图4 (2，1)结尾卷积码优化能量分配前后平均误比特率理论和仿真曲线Fig.4 The theoretic BER curves and simulation BER curves before and after optimizing for a(2，1)convolutional code with tail bits

从图4可以看出能量分配前后系统性能改善不明显，这是因为该结尾卷积码码字每一位的dmin(j)都相同，而且与之对应的nmin(j)也大致相同，从式(4)可以看出码字中每一比特能量的分配主要由dmin(j)和nmin(j)决定，当二者大致都是常数时，Eb(j)也大致为一个常数，即为传统的能量分配，故达不到明显的改善效果.

从以上各图的分析可知:在高信噪比时，本文所提出的能量分配方案适合于多种纠错码，而且当码字中的每一比特位的dmin(j)和nmin(j)相差越大时，该方案起到的效果越好，在低信噪比时，若想得到明显的改善效果，公式(2)需要得到改进，这将也是以后笔者要努力研究的方向.

4 结论

基于一个由一致界推导出的误比特率分布的估算公式，笔者提出了一种新的优化能量分配方案，通过理论推导，该方案为每比特位分配定量的能量，而不是只在系统码和校验码之间分配不同的能量.通过仿真比较显示，该方案适合于不同类型的纠错码，在改善系统误比特率性能方面有很好的效果，而且它不会改变系统的编译码结构，使用时方便简单，容易实现.

［1］TONG S，ZHENG H，BAI B.Precoded turbo code within 0.1 dB of Shannon limit［J］.Electronics Letters ，2011，47(8):521-522.

［2］CHUNG S Y，FORNEY G D，THOMAS J R，et al.On the design of low-density parity-check codes within 0.0045 dB of the shannon limit［J］.IEEE Communictions Letters ，2001，5(2):58-60.

［3］ABBASFAR A，DIVSALAR D，YAO K.Accumulaterepeat-accumulate codes［J］.IEEE Transactions on Communications，2007，55，(4):692-702.

［4］MOHAMMADI A H S，KHANDANI A K.Unequal error protection on turbo encoder output bits［J］.Electronics Letters，1997，33(4):273-274.

［5］BALAMURALITHARE B.A new unequal power allocation scheme for asymmetric turbo code system［J］.Wireless Pers commun，2009，49(1):15-22.

［6］Zhang W，Wang X.Optimal energy allocations for turbo codes based on distributions of low weight codewords［J］.Electronics Letters ，2004，40(19):1205-1206.

［7］邵霞，张卫党.Turbo码误比特率分布的估算［J］.华北水利水电学院学报:2011，32(5):125-127.