一个含有五项的分数阶混沌系统的动力学分析
2019-07-04杨丽新
杨丽新
(陕西科技大学 文理学院, 陕西 西安 710021)
0 引言
分数阶微积分作为数学学科的一个重要分支,是传统的整数阶微积分的推广[1-3].最近十年,分数阶微积分引起了很多学者的关注和研究.分数阶微积分在描述粘弹性系统、电磁波等物理过程中有很重要的应用,并且描述的系统更加精确[4-6].
另一方面,分数阶系统是描述很多的自然现象的有效工具.很多学者提出了不同的分数阶系统,并且研究了它们的动力学行为,文献[7]讨论了分数阶Chua 电路系统的混沌同步问题.另外,研究发现分数阶Chen系统的产生混沌的阶数是0.3,这是到目前为止发现的混沌系统的最低阶数[8].
目前,不同领域的学者对分数阶混沌系统的动力学行为作了广泛的研究并得到了优秀的成果.但是,寻求项数更少的分数阶混沌系统是一个重要的研究方向.在文献[9]中,作者提出了一个含有五项的整数阶混沌系统,并且研究了此系统的丰富动力学行为.
1 分数阶微积分
(1)
式(1)中:q表示分数阶,R(q)表示q的实部,实数a和t分别表示积分的上下限.目前, Riemann-Liouville 和 Caputo 定义是最有效的分数阶微积分定义[10].
Riemann-Liouville (RL) 定义如下描述
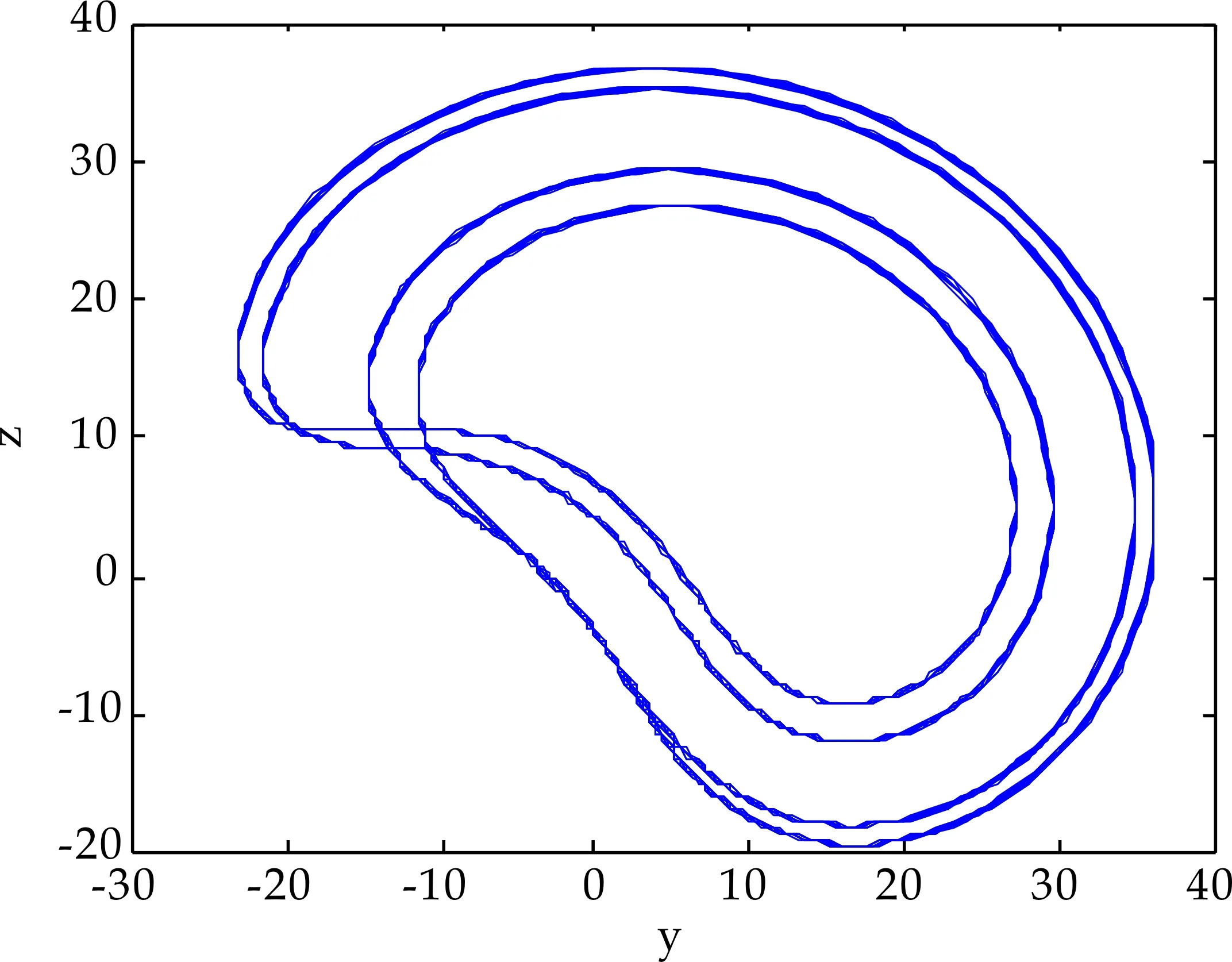
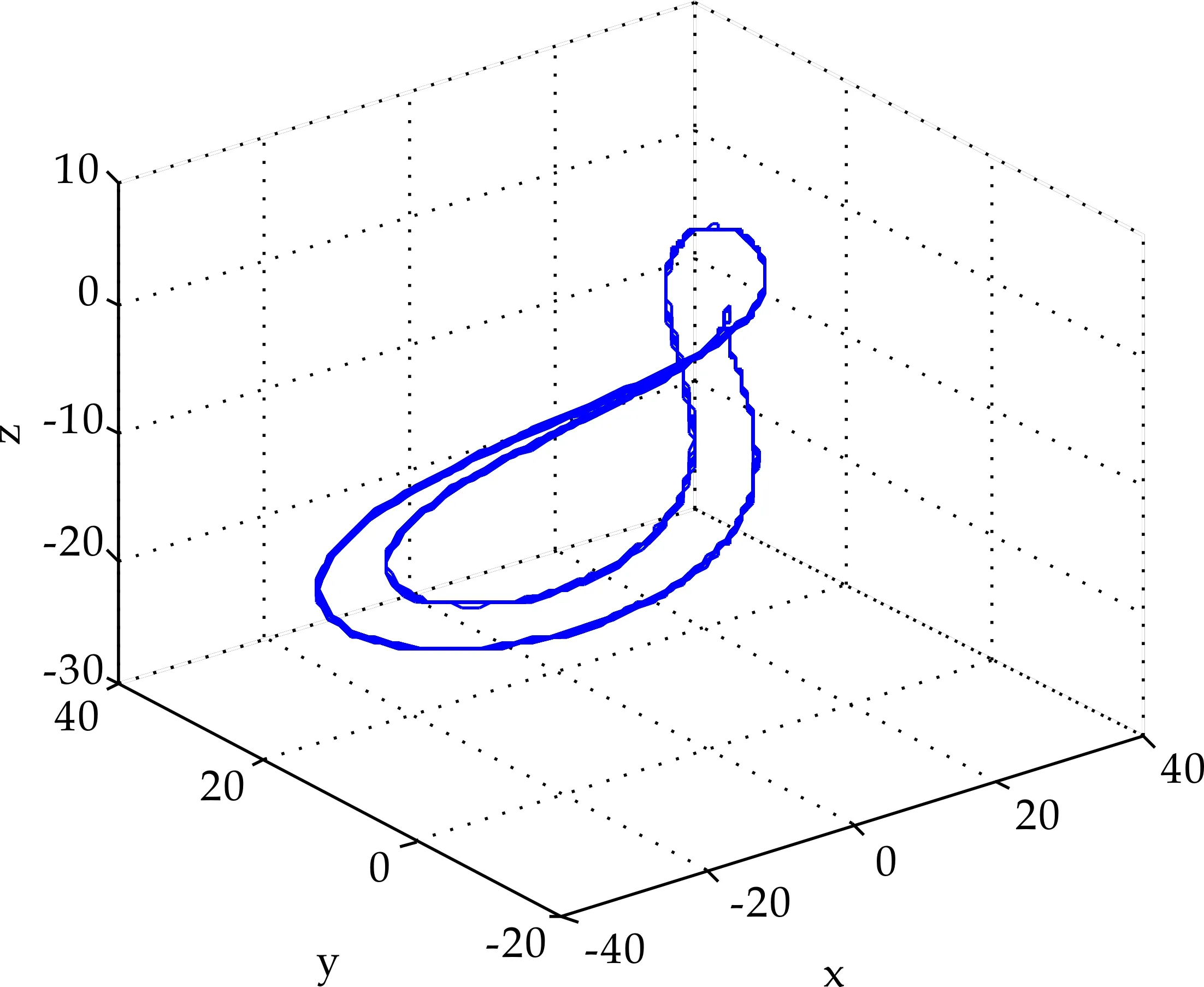
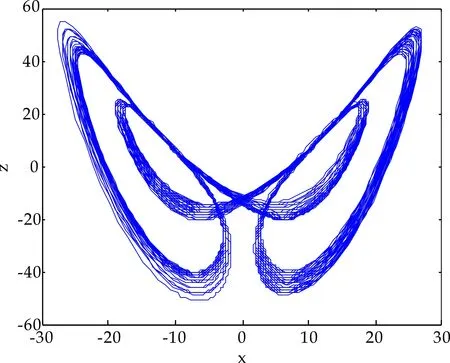
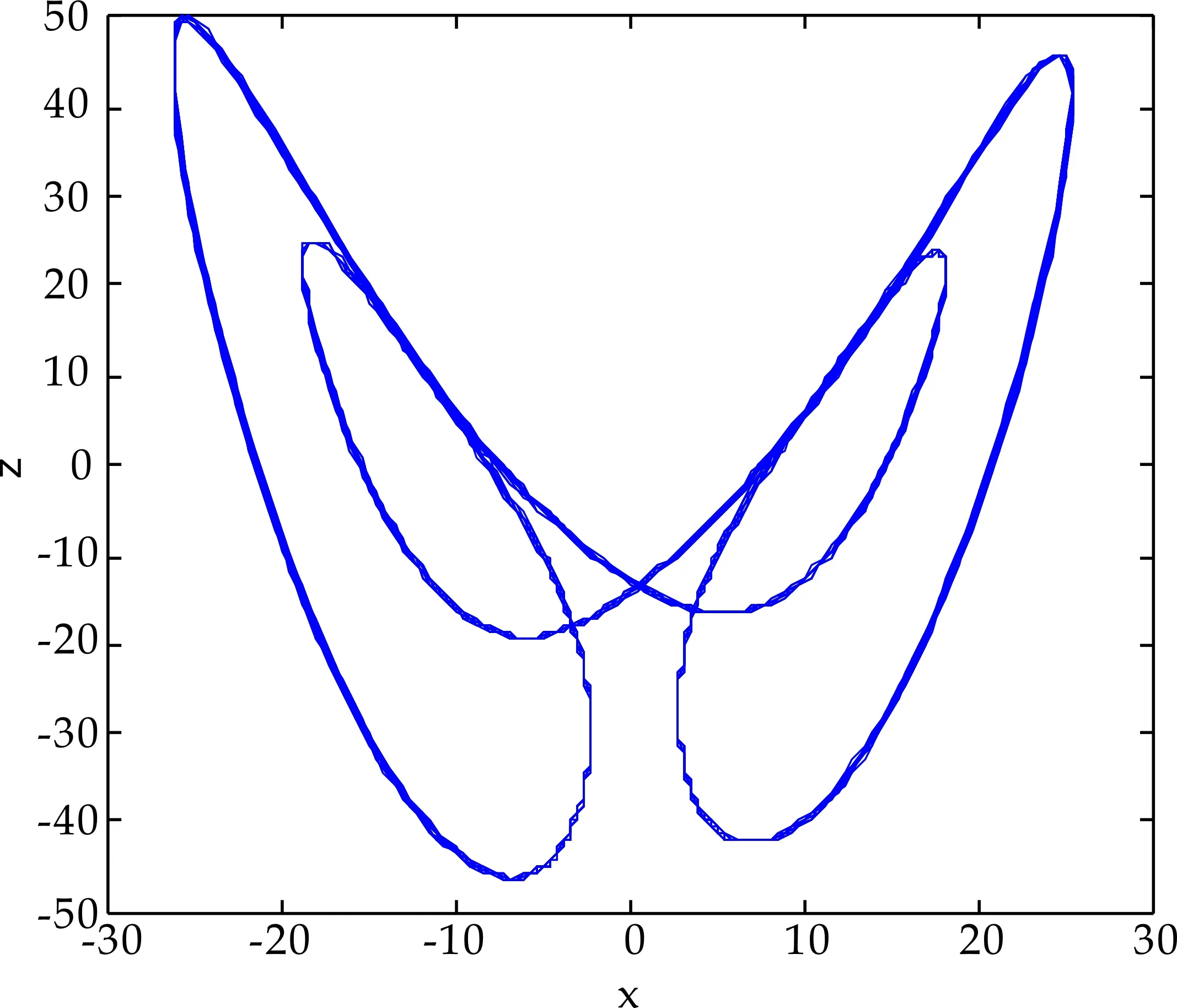
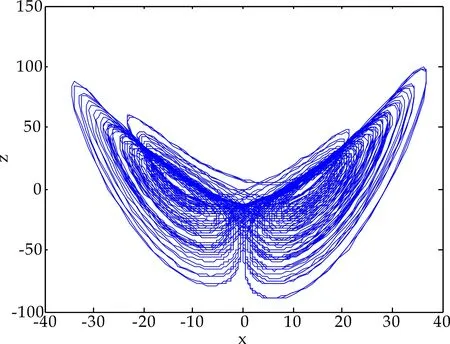
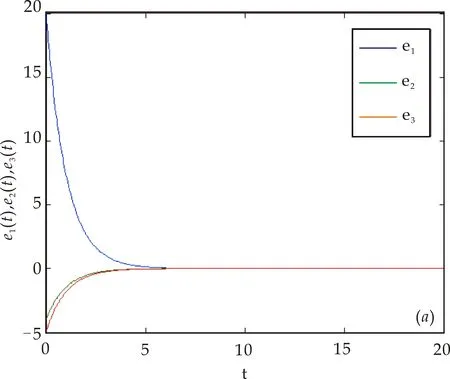
n-1 (2) The Caputo 微积分如下: (3) 式(2)和(3)中:Γ(·)表示伽玛函数如下 整数阶的很多理论不能直接推广到分数阶混沌系统中.接下来,给出分数阶非线性系统的稳定性充分条件[3]. 引理1对于如下的分数阶系统 (4) 渐近稳定的充分条件是矩阵A的特征值满足如下条件: 在文献[9]中,作者构造了一个只含有5项的整数阶的混沌系统,方程如下 (5) 当系统参数取值为a=5,b=90,系统 (5) 有丰富的动力学行为. 接下来,假设系统的阶数是分数阶,则系统(5)对应的分数阶系统可以如下描述: (6) 系统(6)中:qi(i=1,2,3)是分数阶的阶数. 首先,通过下式计算系统(6)的平衡点: (7) 计算可得如下两个平衡点 (8) 并且雅克比矩阵的特征值计算如下: λ1=-7.094 3, λ2=1.470 1+10.544 4i λ3=1.470 1-10.544 4i (9) 根据行列式|λE-J|=0发现矩阵J-和J+有相同的特征值.其中λ1是一个负实数且|arg(λ2,3)|=1.432 3,根据引理1, 若分数阶系统(6)的阶数在0.912≤q≤1.0范围时,分数阶系统(6)的两个平衡点都不稳定. 分岔图是研究混沌系统动力学行为的一个重要工具,因此,在本节内容中,分别以阶数和系统参数作为分岔参数,深入研究系统(6)的动力学行为.对于分数阶混沌系统,在MATLAB仿真中,采取的方法是预估-校正算法,接下来,介绍此方法.首先考虑如下方程 (10) 等式(10) 和如下的Volterra积分方程等价 (11) 令h=T/N,tj=jh,(j=0,1,…,N).则方程(11)的校正式可以离散为如下形式: (12) (13) aj,n+1= 该方法的截断误差是 maxj=0,1,…,N|x(tj)-xh(tj)|=O(hP), 其中p=min(2,1+q). 和整数阶混沌系统相比,分数阶系统的阶数是一个很重要的参数,是影响分数阶混沌系统的动力学行为的关键因素之一.为了验证分数阶吸引子的存在性,选取系统(6)的系统参数为a-5,b=90,以及系统的初始条件为x(0)=1,y(0)=2,z(0)=3,分别调整系统的阶数qi(i=1,2,3)的值,观察系统的动力学行为. 首先,假设系统(6)是等阶系统,也就是说阶数qi(i=1,2,3)取相同的值. 选取系统的阶数分别为q=0.84和q=0.86,系统(6)的正平衡点是一个稳定点,如图1 (a)~(b)所示.继续增加阶数q的值到 0.88,系统(6)的相图呈现出一个混沌吸引子,如图1(c)所示.当阶数q=0.98系统(6)相图还是呈现混沌吸引子,但是和q=0.88的吸引子完全不一样,如图1(d)所示.从这些相图,发现分数阶系统(6)呈现出丰富的动力学行为,接下来进一步借助于分岔图,深入分析系统的复杂动力学行为. (a)阶数q=0.84系统(6)的相图 (b)阶数q=0.86系统(6)的相图 (c)阶数q=0.88系统(6)的相图 (d)阶数q=0.98系统(6)的相图图1 当阶数q取不同值时,系统(6)的相图 为了更加深入地研究分数阶系统(6)的动力学行为,以系统的阶数作为分岔参数,借助于数值仿真的方法,当q∈[0.88,1],系统(6)的分岔图如图2所示.从图2可以看出,当q∈[0.89,0.95]和q∈[0.96,1]范围内时,系统是混沌状态.但是当阶数q=0.95,混沌吸引子突然消失,系统呈现出周期轨道; 当q从0.948变化到0.958.系统发生了鞍结分岔;当阶数q>0.96,系统再一次呈现混沌状态.对应的相图如图3 (a)~(b)所示,可以看出,当系统阶数取不同的值时,系统的吸引子有很大的差别. (a)q=0.95系统(6)的相图 (b)q=0.98系统(6)的相图图3 当q取不同值时,系统(6)的相图 众所周知,对于分数阶系统,不等阶系统的动力学行为比等阶系统的要复杂很多.接下来,固定分数阶数q2=q3=0.98,以阶数q1作为分岔参数,分析系统的动力学行为,当q1∈[0.91,0.99]的分岔图如图4所示,从图4可观察到:当参数q1从0.91开始,经过一系列的倍周期分岔进入混沌状态.例如当q1=0.92时2-周期轨道,当q1=0.93时4-周期轨道.并且,可以观察到混沌系统当参数q1∈[0.975,0.983]时,发生鞍结分岔和霍普夫分岔. 图4 当阶数q1∈[0.91,0.99]时,系统(6)的分岔图 为了更进一步研究系统 (6)的丰富动力学行为,固定系统的分数阶数q1=q2=q3=0.98,调整系统参数a和b.首先以系统参数a作为分岔参数,分岔图如图5所示. 图5 当a∈(5.8,6.2)时,系统(6)的分岔图 从图5可以观察出,当参数a<5.2时,系统(6)呈现出混沌态;当a∈[5.93,6.08]时,系统出现一系列的周期轨道,例如周期1,周期4等等;当分岔参数a>6.08,系统再一次进入混沌态.当a=6.08时,系统发生了霍普夫分岔.不同的参数对应的不同吸引子如图6所示. (a)阶数qi(i=1,2,3)=0.98、a=5.2,系统(6)的相图 (b)阶数qi(i=1,2,3)=0.98、a=6.8,系统(6)的相图 (c)阶数qi(i=1,2,3)=0.98、a=7.3,系统(6)的相图 当选取分数阶的阶数为q1=q2=q3=0.91,系统参数a=5,调整系统的另一个参数b,观察系统的动力学行为. 通过大量的数值计算和仿真,对于参数b,系统(6)的动力学行为可以概括如下: (1)当参数b≤175,系统呈现周期轨道,如图7(a)所示; (2)当参数175 (3)当参数b>193,系统呈现出一个混沌吸引子,如图7(c)所示. 通过选取不同的分岔参数,对系统(6)的动力学行为进行了详细研究,结果表明,新系统的阶数和系统的参数都对它的动力学行为产生很大的影响,不同的阶数和参数,系统的吸引子有很大的差异. (a)阶数q1=q2=q3=0.91、b=175,系统(6)的相图 (b)阶数q1=q2=q3=0.91、b=180,系统(6)的相图 (c)阶数q1=q2=q3=0.91、b=200,系统(6)的相图图7 系统的阶数值为q1=q2=q3=0.91,当参数b 取不同的值时,系统(6)的相图 在本小节内容,主要研究分数阶新系统的投影同步问题.非线性系统的同步在各个领域具有很大应用前景,很多学者提出不同类型的同步.例如完全同步、相同步、内同步、外同步研究结果已有很多[11-15].但是投影同步是比较重要的一类同步形式,接下来给出投影同步的定义[16].假设驱动系统和响应系统的方程分别如下描述: (14) (15) 其中:x=(x1,x2,…,xn)∈Rn,y=(y1,y2,…,yn)∈Rn分别是状态向量;q∈(0,1]是分数阶数.f,g:Rn→Rn是连续的非线性函数,U(t,x,y)是待设计的控制器.对于驱动系统(14)和响应系统(15),当且仅当下式成立 (16) 则称两个系统实现了投影同步. 其中M(t)=diag(φ1(t),φ2(t)),…,φn(t))是标度矩阵. 对于分数阶新系统(6),构造驱动系统和响应系统分别如下: (17) (18) 为了实现驱动和响应系统的同步,首先定义误差系统如下: (19) 图8 驱动系统(17)和响应系统(18)的误差曲线随时间的演化过程(当标度矩阵选取为M(t)=diag(sin(πt),1,2)时) 根据误差系统,设计如下的控制器: (20) 为了验证设计控制器的有效性,借助数值仿真验证,误差曲线随时间的演化过程如下: 从图8可以看出,误差曲线随着时间的演化最后趋于零,表明驱动和响应系统在控制器的作用下,实现了投影同步. 本文提出了一个新的分数阶混沌系统.首先,从理论上研究了系统的一些基本特征.其次,借助于数值仿真的方法,调整系统分数阶数和系统参数,得到系统在不同条件下的吸引子以及分岔图.研究结果表明,分数阶新系统有不同的分岔行为,包括倍周期、霍普夫、鞍结分岔等形式.最后,对分数阶新系统的投影同步进行了研究,设计了合理有效的控制器,实现了驱动和响应系统的同步控制.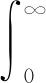
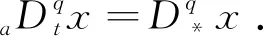
2 分数阶新系统的稳定性分析
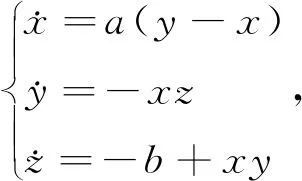
3 分数阶新系统的分岔行为研究
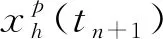
3.1 系统阶数作为分岔参数
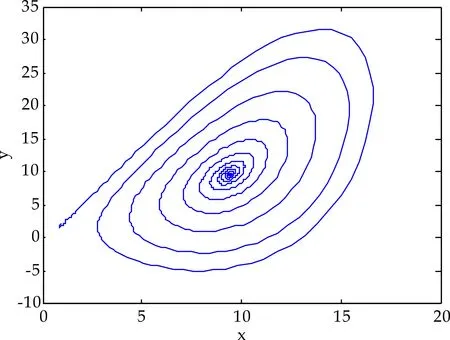
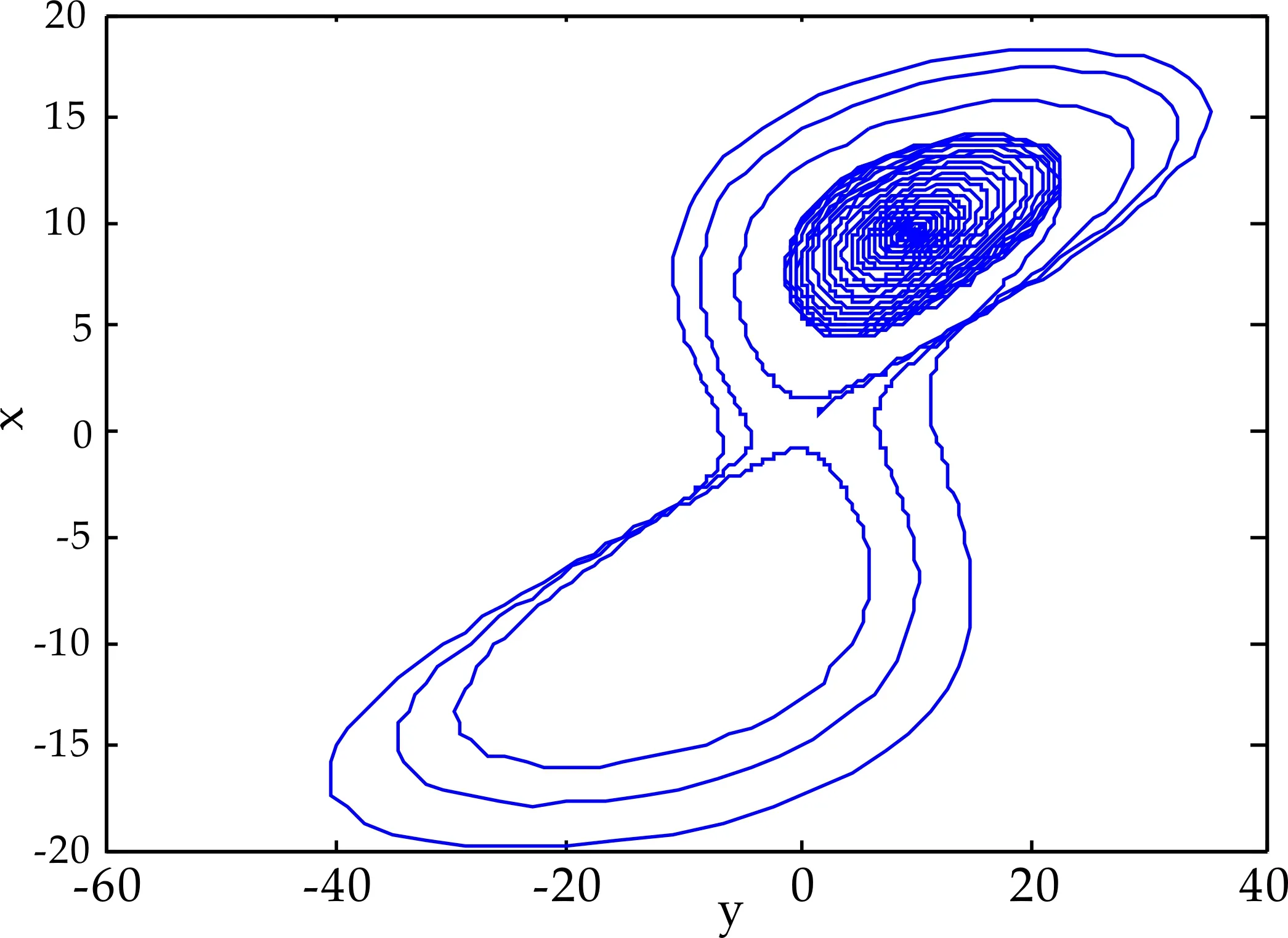

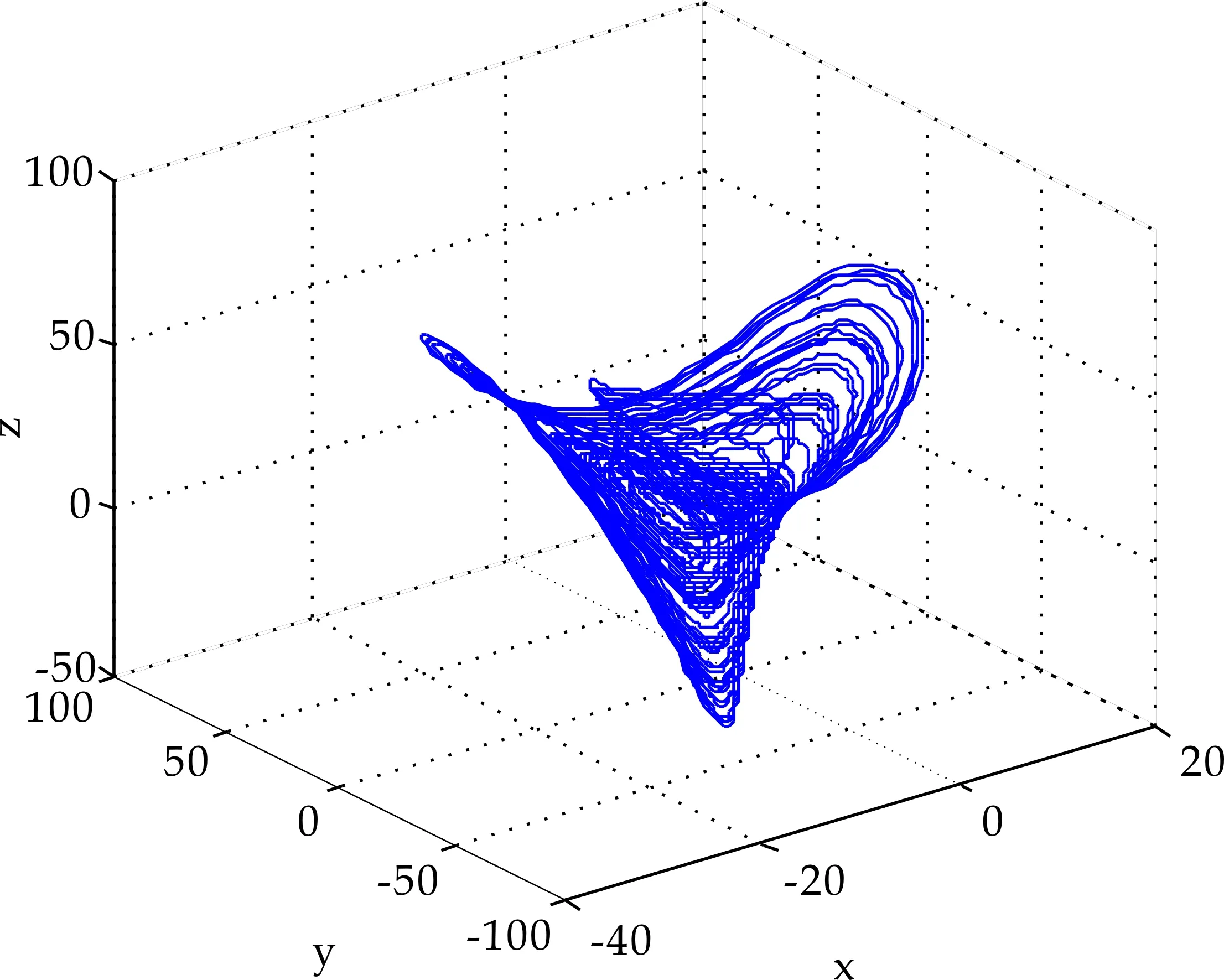
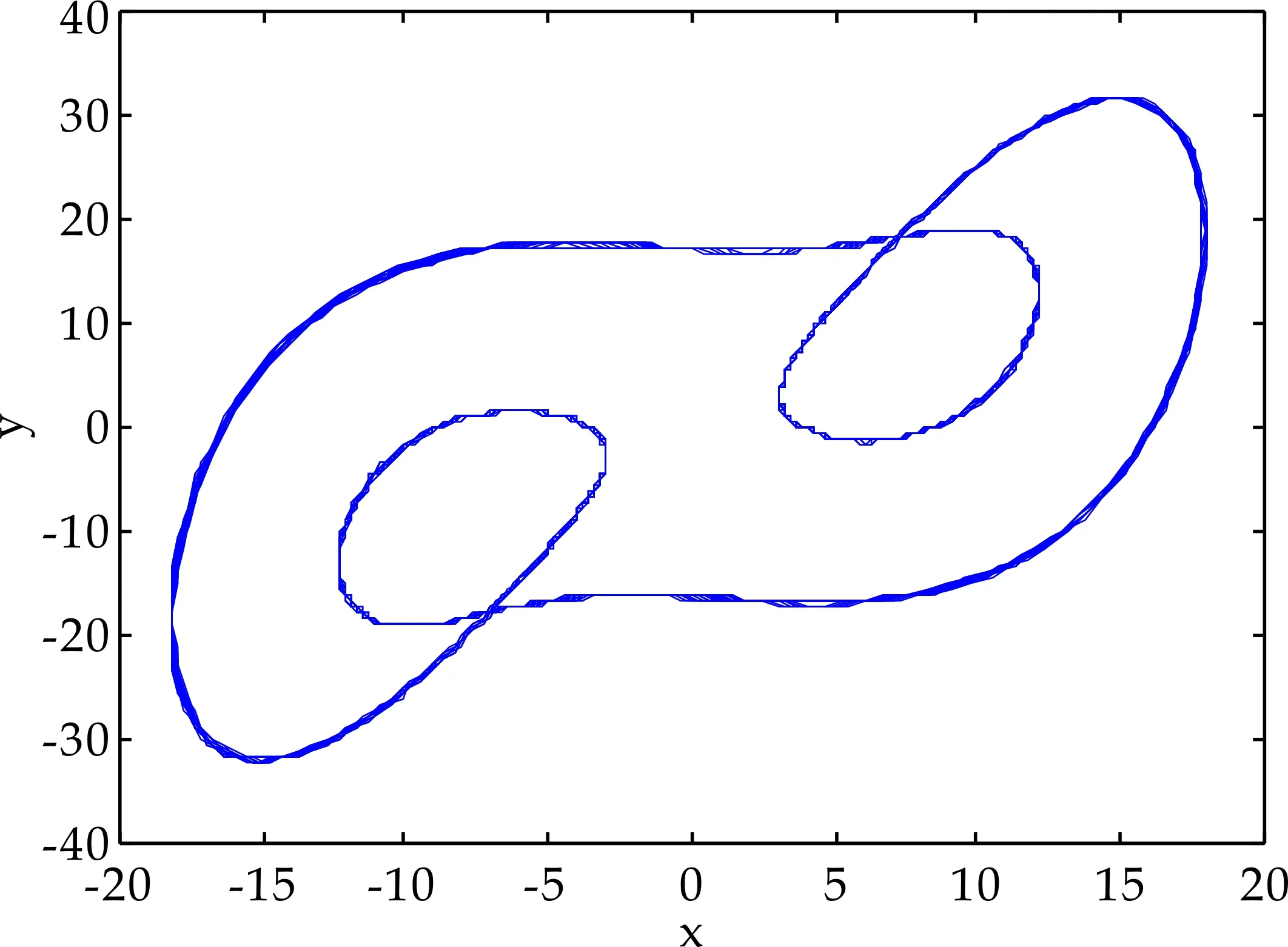
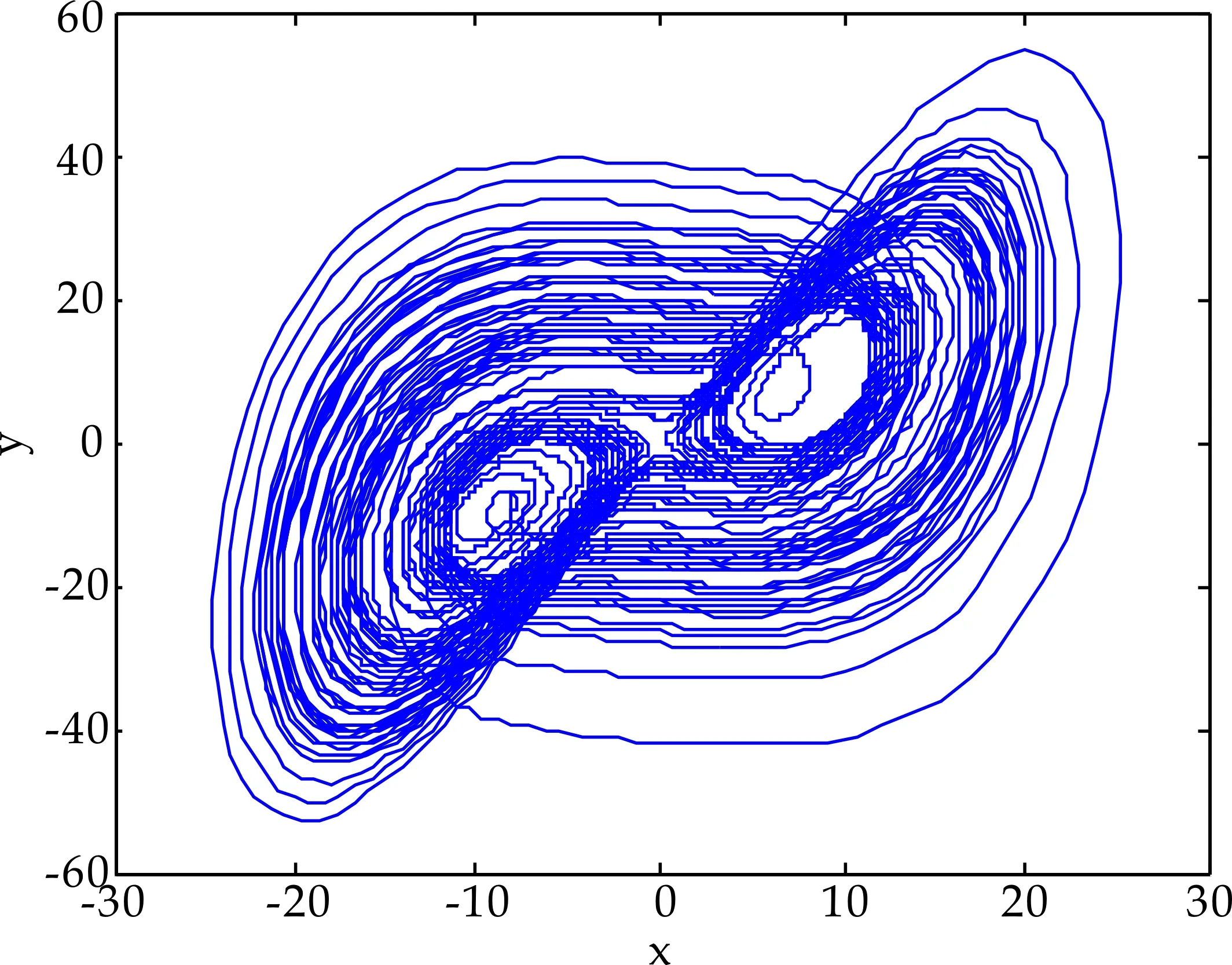
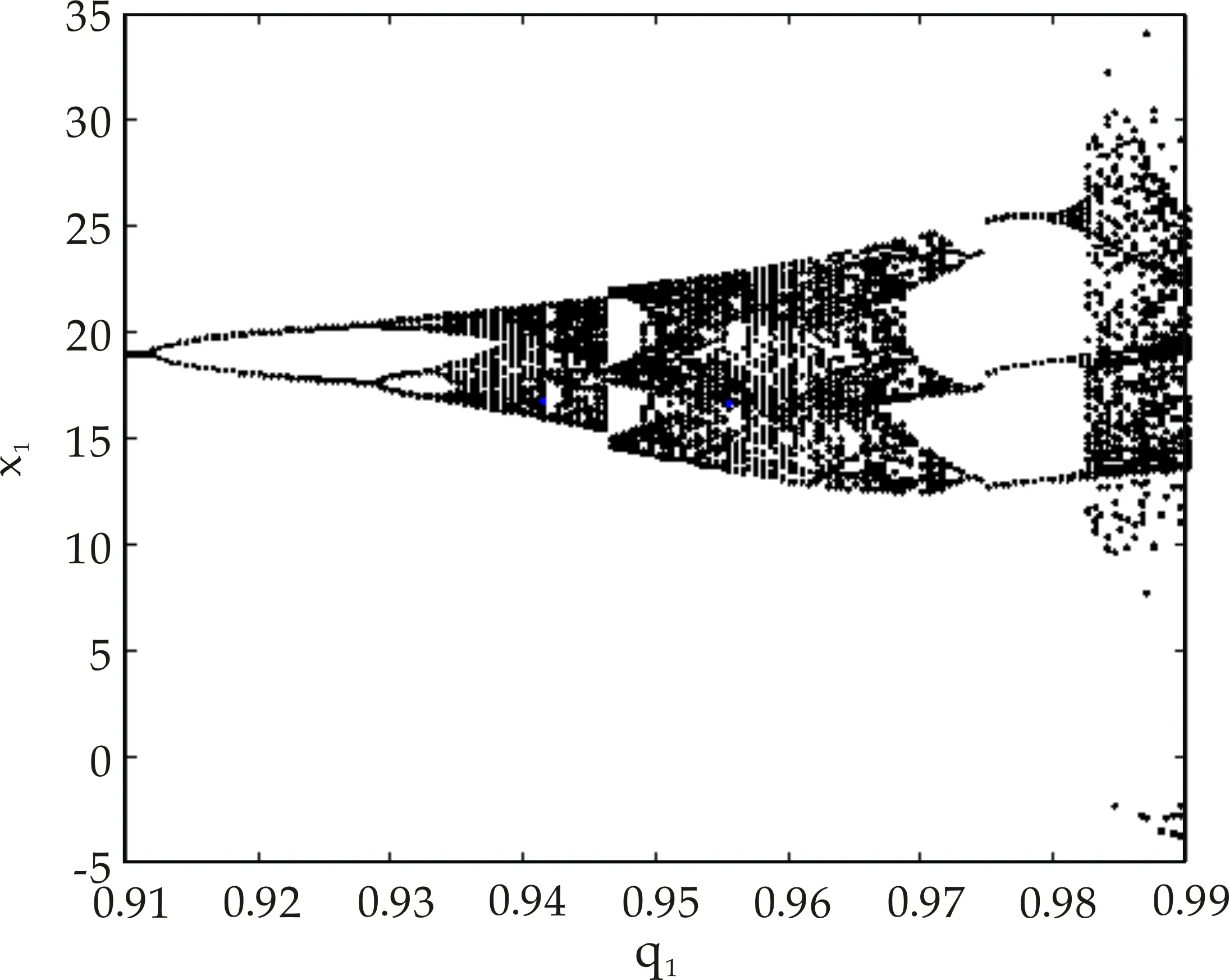
3.2 系统参数作为分岔参数
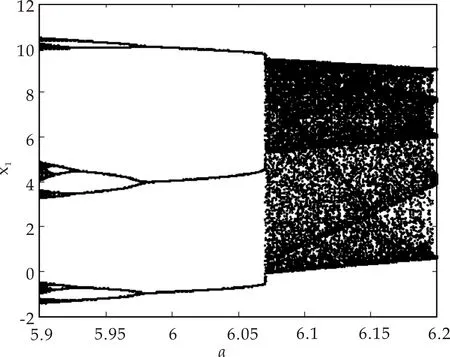
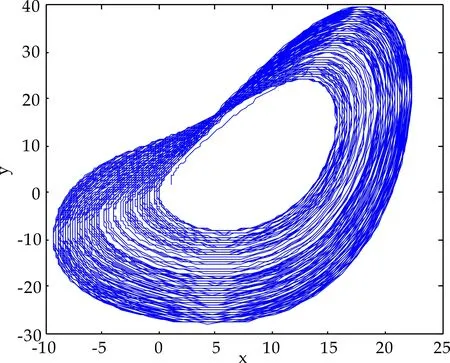
4 分数阶新系统的投影同步
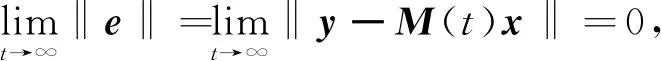
5 结论
