结合分解技术的多目标引力搜索算法

毕晓君，刁鹏飞，王艳娇，肖 婧

（1.哈尔滨工程大学信息与通信工程学院，150001哈尔滨；2.东北电力大学信息工程学院，132012吉林吉林；3.辽宁省交通高等专科学校信息工程系，110122沈阳）

结合分解技术的多目标引力搜索算法

毕晓君1，刁鹏飞1，王艳娇2，肖 婧3

（1.哈尔滨工程大学信息与通信工程学院，150001哈尔滨；2.东北电力大学信息工程学院，132012吉林吉林；3.辽宁省交通高等专科学校信息工程系，110122沈阳）

针对基于分解的多目标遗传算法在解决多目标问题时无法有效解决前沿面非均匀、不连续的问题，提出一种基于分解技术的多子群串行搜索的多目标引力搜索算法（MOGSA／D）.为充分利用算法优化分解出的目标函数所得到的进化信息、提高收敛速度，采取多种群串行的搜索方式；针对理想前沿面为非超平面的情况，提出一种预测理想前沿面形状的方法，并针对预测结果选择适合的权重系数生成方式；为提高解集的整体质量，提出一种基于目标权值的策略删减种群.通过标准测试函数的实验验证，所提算法与其他多目标进化算法相比在解集的收敛性以及分布性上均有较大提高，验证了算法的有效性.

引力搜索算法；多目标优化；分解；多种群策略

多目标优化问题MOP（multi-objective optimization problem）需要同时优化2个或2个以上的目标函数，且各个优化目标之间通常是相互冲突的，因此不存在能使所有目标都达到最优的解.

多目标进化算法MOEA（multi-objective evolutionary algorithm）是目前广泛采用的一种解决MOP的方法，主要可以分为3类：1）基于Pareto占优关系的MOEA算法，如ε-占优机制［1］、E-占优机制［2］；2）基于评估指标的MOEA算法，如HypE［3］等算法；3）基于分解技术的MOEA算法，如MOEA／D算法［4］.其中基于分解的MOEA算法因其计算简单、复杂度小和收敛性好受到广泛关注，但当理想前沿面为不连续、非均匀等形状时，所得到的优化结果的收敛精度及稳定性还有待进一步提高.

引力搜索算法GSA（gravitational search algorithm）是2010年提出的群智能优化算法，具有设置参数少、全局搜索能力强、计算简单、收敛速度快等优点［5］.本文将GSA与分解技术相结合，提出一种基于分解技术的多目标引力优化算法.主要创新点：1）采用分解技术，将多目标问题分解成单目标问题，然后采用多子群串行搜索的策略对各子问题展开优化，提高进化搜索的效率；2）提出一种理想前沿面的预测策略，并根据预测结果选取适合的权重系数计算方式，一定程度上保证了解集分布的均匀性；3）针对解在各目标所得结果的线性加权和，提出一种种群删减策略，提高了解集相对于理想前沿面的逼近性及分布的均匀性.

1 引力搜索算法及基于分解的多目标算法

1.1 引力搜索算法

可以把种群中的个体想象成是一组在空间中运动的粒子，它们在万有引力的作用下，相互运动，其质量的大小是评价解优劣的标准，质量较大粒子的位置对应较优解.粒子通过相互作用、相互运动实现进化信息的共享，从而向最优区域展开搜索.

设空间中含有N个粒子，则第i个粒子的位置表示为

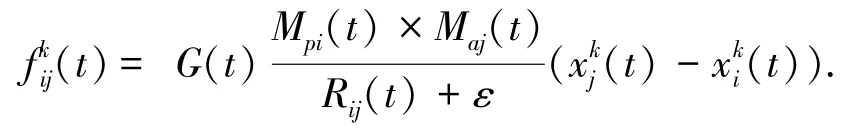
式中：Maj（t）和Mpi（t）分别为粒子j和粒子i的质量；ε是一个极小的常量；G（t）表示在t时刻的万有引力常数，具体定义为

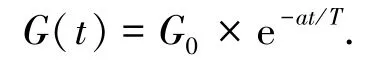
式中：T为设置的最大迭代次数，G0为初始时刻的引力常数，Rij（t）为粒子i与粒子j之间的欧氏距离．则在t时刻，粒子i在k维上受到的其他粒子的合力为

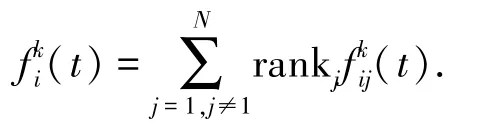
式中：rankj为变化区间在［0，1］之间的随机数；为粒子j对粒子i在第k维空间上的作用力．依据牛顿第二定律，定义t时刻粒子i在k维上的加速度为

在进化过程中，粒子的速度和位置的更新方式为

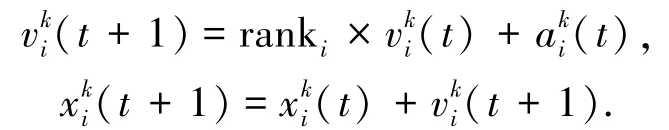
粒子的质量与适应度值有关，质量越大的粒子越接近最优，并且它对其他粒子的作用力相应会更大，但移动速度较慢.粒子质量的计算方式为

式中：fi（t）为粒子i的适应度值；w（t）为质量最小粒子的适应度值；b（t）为质量最大粒子的适应度值．

图1给出了GSA算法的操作流程图.

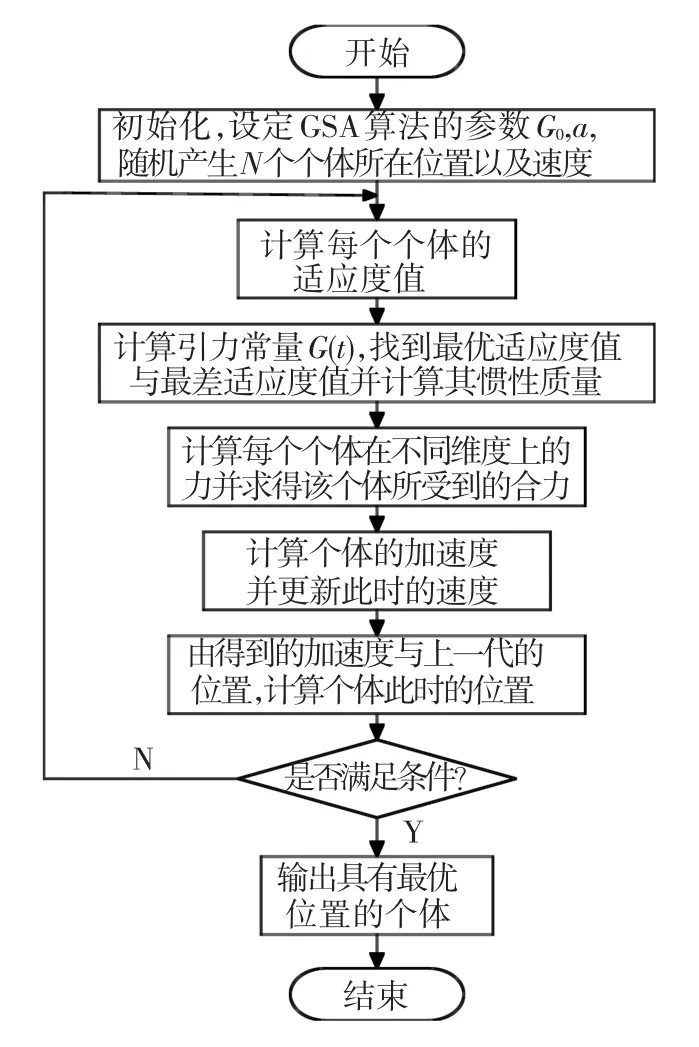
图1 GSA算法流程图

1.2 基于分解的多目标算法

基于分解的多目标优化算法结合了多目标局部搜索和多个单目标Pareto抽样的优点，而切比雪夫法又是其中解决效果最好的方法.在切比雪夫分解模型下，对于一个给定的权重向量，对应的单目标子问题可描述为

式中：权重向量λ=（λ1，…，λm）满足λk≥0且为参考点，是由解集在各个目标函数上取得的最优值构成的虚拟点，对于最小化问题有z∗i=min｛fi（x）｜x∈Ω｝，1，2，…，m．在满足条件的情况下，对于任意一个给定的权重向量，存在一个使式（1）达到最小的最优解，该最优解就是原多目标优化问题的一个Pareto最优解.所以，可以通过设定N个不同的权重向量获得N个最优解来构成Pareto最优解集．

2 基于分解的多目标引力搜索算法

提出一种基于分解技术的多目标引力搜索算法（MOGSA／D）.首先选取几组具有偏好性的权重系数展开优化搜索，并以此判别理想前沿面的形状.然后基于预测结果选取适合的权重系数计算方式.种群在对分解后的优化问题展开搜索时，相邻子问题的解具有相似性，因此为充分利用这种近似性，提高求解能力尤其是非均匀不连续问题的优化效率，采用多子群串行搜索的策略.最后为提高解集的收敛精度并兼顾粒子分布的均匀性，提出一种基于目标权值的策略对种群进行删减.

2.1 权重的自适应选取

MOEA／D通过构造多组权重系数将一个MOP分解为一组单目标优化问题，并通过子问题之间的合作来同时优化这组子问题，从而获得对理想最优解集的一个逼近.但该方法存在2个问题：

1）传统MOEA／D算法采用的权重系数生成方法是基于理想面是超平面的情况.针对理想面非均匀的情况，单一的权重系数生成方式会影响解集分布的均匀性，如图2所示.

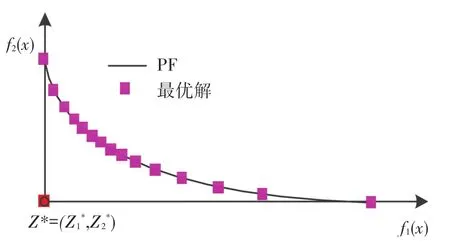
图2 分布非均匀前沿面

2）当前沿面不连续时，若算法对处在断开区域的子目标问题进行优化求解，则由于进化压力容易得到相同的解，势必会浪费计算资源，降低算法的整体优化性能，如图3所示.

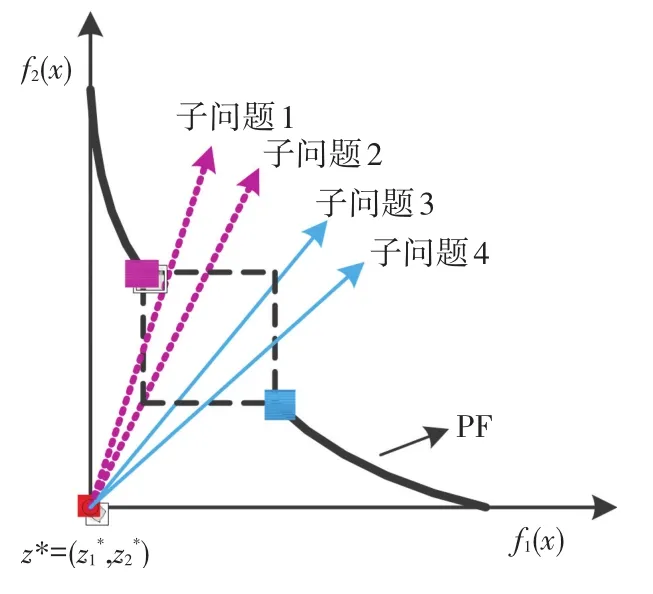
图3 分布不连续前沿面

为解决上述问题，文献［6］提出权重向量根据其自身的最优解进行自适应调整，文献［7］提出一种加强的权重向量调整方法.但这些方法所适用的前提条件是理想前沿面是超平面的情况，当前沿面为非超平面或不连续时，上述方法均不能保证所得解集分布的均匀性，且会浪费计算资源.因此，权重系数的生成必须针对不同的前沿面形状自适应产生.

基于以上分析，首先对理想前沿面的形状进行预测.通过选择具有明显偏好性的权值系数可以得到理想前沿面的边界点，若理想前沿面为超平面，则对2个目标问题有判别方式为

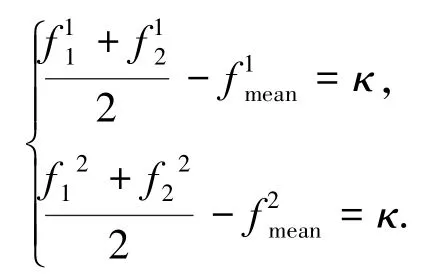
理论证明：当理想前沿面是超平面时，则对2个目标问题是一条直线，在极端情况下，当权重向量的取值为（1，0）时，所得的最优解在2个目标函数上的解是这条前沿面上的一个端点；同理，当权重向量取值为（0，1）时为前沿面的另一个端点；对一个等腰直角三角形，角分线也是中位线，即取权重向量为（0.5，0.5）时，所得的解应位于前沿面的中点位置上．

对3个目标问题，可判断点和面的位置关系，即通过求解4组权重系数构成的子问题的最优值，判断理想前沿面的形状．设4组偏好权重系数构成的

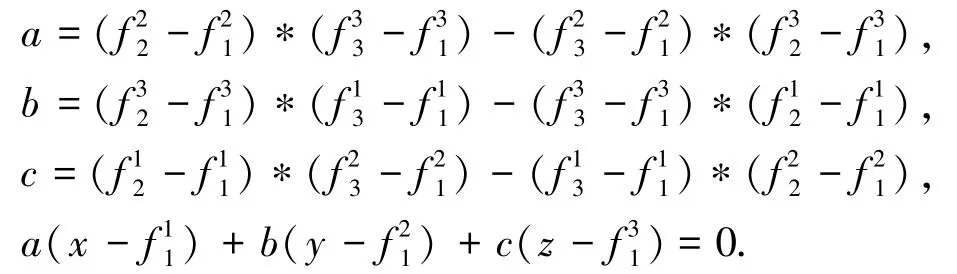
根据得到的平面方程，通过比较点和面的位置关系得到前沿面的预测结果，具体描述如下：

若

若

若

当预测到前沿面形状后，针对不同的预测结果，为有效解决非均匀不连续前沿面问题，必须保证权重系数构成的向量与前沿面的焦点均匀分布在前沿面上.提出一种权重系数的生成方式为

1）当前沿面为超平面时，则p取值为1，即λ构成的面也为超平面；

2）当前沿面为凸平面时，则p取值为2，即λ构成的面也为凸平面；

3）当前沿面为凹平面时，则p取值为0.5，即λ构成的面也为凹平面．

2.2 多子群串行搜索

对于非连续理想前沿面，由于进化压力的驱使，必然会导致几组相似权重系数所构建出的子问题具有相同的解.为解决前沿面不连续所带来的资源浪费问题，结合GSA的收敛速度快、求解精度高、进化步长可控等特性，采取多子群串行搜索的策略对构造出的子问题进行优化.相邻权重系数所对应的解也具有相似性，根据这种相似性，可以为下一个种群粒子的初始化设定一个较小的范围，相比于在整个空间随机初始化种群缩小了搜索区域，提高了种群搜索最优解的速度.因此，当一个子种群完成对其优化问题的求解时，参考此前最优解初始化种群，粒子生成方式为

2.3 删减策略

为了利于决策者的选择，提高解集中解的代表性，需要对优化得到的最优解集进行筛选，以提高其分布的均匀性及收敛程度.以最小化问题为例，能够使各目标值都取较小的点，将更容易支配其他的解也即更靠近理想前沿面，但对互不支配的2个解则较难判断其优劣.对此，通过比较2个相似非支配解在各目标上整体的逼近程度加以删减.对非支配解尤其是较为相似的2个解，可通过计算其归一化后的各目标值的加权和进行筛减，具体描述如下：

将解集中各粒子按照欧式距离进行排序，对于相对距离小于阈值u的2个粒子，先分别将各目标值归一化，然后计算其各目标上的加权和，即

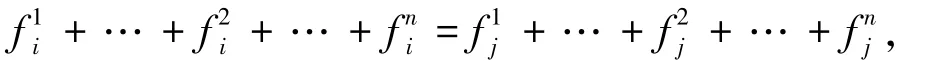
则说明此时2个解相同，任意删除一个．若

则第j个解优于第i个解，删除第i个解．

基于目标加权和的判定方式，可以较好地对相似非支配解进行删减，使最终得到的解集更佳逼近前沿面.对于拥挤区域的删减，在一定程度上保证了分布的均匀性，同时，降低了决策者的选择压力.

2.4 算法实现流程

步骤1算法初始化，设定问题维数D，种群规模N1和N2以及2个种群各自的最大迭代次数，问题的函数评价次数，以及κ、u、G0、a、H．

步骤2对多目标问题的个数，选择相应的几组偏好权值系数（若目标个数为2，则选择3组带有偏好性的权值系数，若目标个数为3，则选择4组带有偏好性的权值系数）构成目标函数.

步骤3计算每个个体的适应度值，并求出其相应的惯性质量.

步骤4根据个体的惯性质量，求得每个个体所受的合力，进而求得其加速度.

步骤5判断是否满足终止条件，若不满足转到步骤3.

步骤6当完成对各组偏好权重系数构成的单目标函数的求解后，采用式2.1节描述的方法判断前沿面的形状.若前沿面形状是凹的，则p=0.5；若前沿面形状为凸的，则p=2；否则p=1，具体的权重系数生成方式如2.1节所示.

步骤7根据得到的一系列权重系数，按步骤3、步骤4进行优化搜索.

步骤8当满足终止条件时，重新初始化新的子种群，初始化方式采用式（2）所示方式进行.

步骤9当达到最终的函数评价次数后，采用删减策略对解集进行删减，即将解集中各粒子按照欧式距离进行排序，对于相对距离小于阈值u的2个粒子，先分别将各目标值归一化，然后计算并比较粒子各目标上的加权和，保留较优粒子.

步骤10输出最终的解集.

3 仿真实验与结果分析

所有实验在硬件配置为Intel®CoreTM2 Duo CPU P7570 2.26 GHz、2 G内存、2.27 GHZ主频的计算机上进行，开发环境为Matlab2 010.b.

3.1 测试问题

实验选用二目标ZDT和三目标DTLZ两个系列的多目标测试函数［8］，具体包括ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1和DTLZ2等7个函数.这些测试函数具有理想前沿面形状为凹形、凸形、不连续以及多模等特点，可验证所提算法的有效性.

采用世代距离指标（generational distance metric，GD）和空间度量指标（spacing metric，SP）［9-10］两种评价标准测试所提算法的性能.GD和SP的定义为

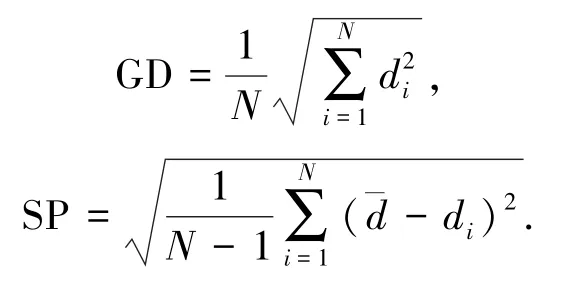
式中：N表示通过算法求得的解集中解的个数；di为求得的解集中第i个解到理想最优解集的最小欧几里得距离；¯d为算法求得所有解di的平均值．

GD的值越小，表明算法求得的解集与问题的理想最优解集越接近，算法收敛性越好.SP的值越小，表明算法求得的解集中的解分布的越均匀，算法的均匀性越好.

3.2 参数设置

实验结果与目前解决多目标问题效果较好的NSGAII［11］，MOEA／D-AWA［7］，Adaptive-MOEA／D［12］和HMOEA［9］进行了比较，相关参数如表1所示.

选取的二目标偏好权重向量个数为3，即分别偏好2个目标的向量，以及任意选取的向量分别为（0.99，0.01）、（0.01，0.99）、（0.5，0.5）；选取的三目标偏好权重系数个数为4，即分别偏好3个目标的权重向量以及任意选取的一组向量，分别为（0.90，0.05，0.05）、（0.05，0.90，0.05）、（0.05，0.05，0.90）、（0.33，0.33，0.34）.

表1 参数设置

3.3 多子群串行搜索策略验证

为验证多子群串行搜索策略在解决多目标问题时的有效性，通过观察算法对测试问题搜索的渐变过程进行实验，验证多子群策略的有效性.函数ZDT3具有前沿面不连续的特点，因此选取该函数作为实验函数.实验结果如图4所示.

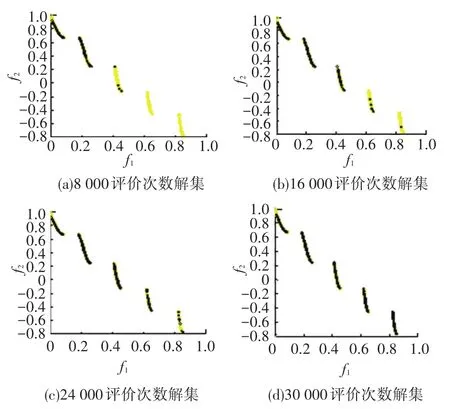
图4 随迭代得到解集的渐进变化趋势

从图4可以看出，随着函数评价次数的不断增加，所得到的解集逐渐遍布了整个理想前沿面，取得了较好的逼近效果，说明多子群串行搜索的有效性.图中出现离散点，这是因为对子问题的搜索会产生一些非支配解，这些解对于当前子问题不是最优解但对于其他子问题来说则是最优解，体现了多种群串行搜索策略在优化多目标问题时，不会漏掉得到的较优解，具有较好的全局搜索性能.

3.4 删减策略有效性验证

为验证删减策略在解决多目标问题中的有效性，选取测试函数ZDT1进行验证，实验结果如图5所示，指标SP和GD的对比如表2所示.

图5 删减前后算法所得前沿面对比

表2 解集在删减前后的GD值和SP值

从图5可以看出，在算法未对解集进行删减时，所得到的前沿面存在较多被支配解，当对其进行删减后，得到的解集则是由一群非支配解构成.由表2可以看出，采取删减策略对解集进行删减后，指标GD和SP均得到较大的提升，即得到的解集无论是收敛性还是均匀性均得到了提高，验证了删减策略的有效性.

3.5 求解性能对比

主要考察MOGSA／D算法与对比算法在标准测试函数上的性能比较，测试结果如表3及表4所示.其中表3给出各算法在优化各问题时所得GD指标的均值及方差，表4给出各算法在优化各测试问题时所得SP指标的均值及方差.

从表3中可以看出，对于ZDT1、ZDT2、ZDT3和ZDT4等4个测试函数，MOGSA／D算法在指标GD以及指标SP上都取得了优于其他对比算法的性能，也即收敛性以及分布性都是最好的；对函数ZDT6以及函数DTLZ2，MOGSA／D算法的GD是最小的，也即收敛性是最好的，分布性指标也仅次于MOEA／D-AWA；对函数DTLZ1，MOGSA／D算法在收敛性指标上没有得到较好的效果，但分布性仍优于其他对比算法.综合来看，在求解ZDT和DTLZ问题上，本文所提算法无论在收敛性、鲁棒性还是分布性上均优于其他同类算法.

表3 各算法的GD值（第一行）及其标准差（第二行）

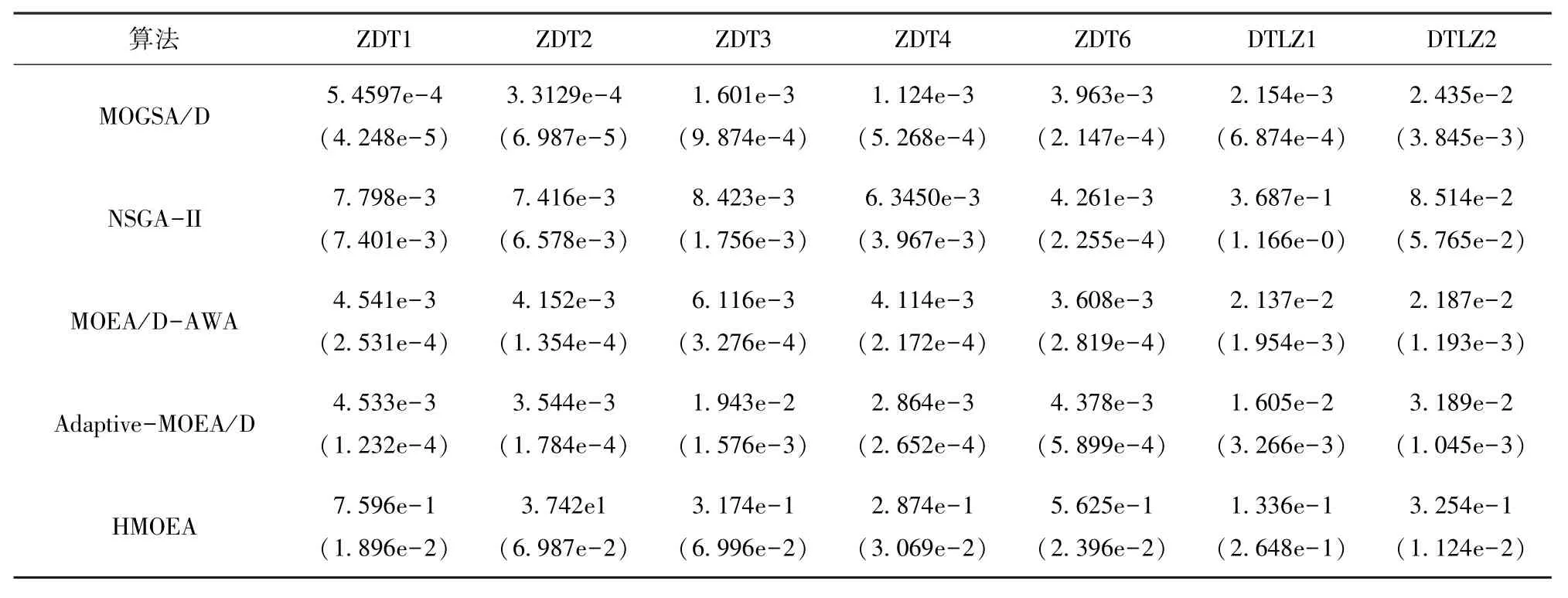
表4 各算法的SP值（第一行）及其标准差（第二行）

4 结 语

基于分解的多目标引力搜索算法MOGSA／D，通过对理想前沿面的估计，自适应选取与之匹配的权重系数生成方式；采用多子群串行搜索各子目标问题方法，为充分利用子问题的相似性，提出一种扰动生成新种群的策略；根据所得解集中粒子间的拥挤度，提出一种基于各目标加权和的方式删减较劣解，以保证解集更均匀地逼近理想前沿面.通过对测试函数集ZDT和DTLZ上的实验证明，MOGSA／D算法与现有的MOEAs相比，具有更好地收敛性及和分布的均匀性.

［1］HERNÁNDEZ-DÍAZA，SANTANA-QUINTERO L，COELLO COELLO C，et al.Pareto-adaptive∈-dominance［J］. Evolutionary Computation，2007，15（4）：493-517.

［2］郭思涵，龚小胜.正交设计的E占优策略求解高维多目标优化问题研究［J］.计算机科学，2012，39（2）：276-279，310.

［3］BADER J，ZITZLERE.HypE：an algorithm for fasthypervolumebased many-objective optimization［J］.Evolutionary Computation，2011，19（1）：45-76.

［4］LIHui，ZHANGQingfu.Multiobjective optimization problems with complicated pareto sets，MOEA／D and NSGA-II［J］. IEEE Transactions on Evolutionary Computation，2009，13（2）：284-302.

［5］RASHEDI E，SARYAZDI S.GSA：a gravitational search algorithm［J］.Information Sciences，2009，179（13）：2232-2248.

［6］WANG R，PURSHOUSE R C，FLEMING P J.Preferenceinspired co-evolutionary algorithm using weights for manyobjective optimization［C］／／Proceeding of the fifteenth Annual Conference Companion on Genetic and Evolutionary Computation Conference Companion.New York：ACM，2013：101-102.

［7］QIYutao，MA Xiaoliang，LIUFang，et al.MOEA／D with adaptive weightadjustment［J］.Evolutionary Computation，2014，22（2）：231-264

［8］TAN Yanyan，JIAO Yongchang，LIHong，etal.MOEA／D+ uniform design：a new version of MOEA／D for optimization problems with many objectives［J］.Computers＆Operations Research，2013，40（6）：1648-1660.

［9］TANG L，WANG X.A hybrid multiobjective evolutionary algorithm for multiobjective optimization problems［J］. IEEE Trans on Evolutionary Computation，2013，17（1）：20-45.

［10］SIMON D.Biogeography-based optimization［J］.IEEE Transactions on Evolutionary Computation，I2008，12（6）：702-713.

［11］DEB K，PRATAP A，AGARWAL S，et al.A Fast and elitistmultiobjective genetic algorithm：NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2），182-197.

［12］SUCIU M，PALLEZ D，CREMENE M，et al.Adaptive MOEA／D for QoS-based web service composition［M］. Berlin：Springer，2013.

（编辑王小唯）

M ulti-objective gravitational search algorithm based on decom position

BIXiaojun1，DIAO Pengfei1，WANG Yanjiao2，XIAO Jing3
（1.College of Information and Communication Engineering，Harbin Engineering University，150001 Harbin，China；2.College of Information Engineering，Northeast Dianli University，132001 Jilin，Jilin，China；
3.Dept.of Information Engineering，Liaoning Provincial College of Communications，110122 Shenyang，China）

When the ideal frontier is discontinuous or inhomogeneous，the multi-objective evolutionary algorithm can’t solvemulti-objective problems effectively by decomposition.In order to improve this situation，a novelmultiobjective gravitational search algorithm based on decomposition（MOGSA／D）is proposed.In MOGSA／D，the multi-population serial strategy is good for the population study evolutionary information.According to shape prediction of ideal frontier，a suitable generation method of weight coefficient is selected.A pruning strategy is adopted to prune the solution set.Experimental results show that MOGSA has a good performance to solve multiobjective problems in comparison with othermulti-objective optimization algorithms.

gravitational search algorithm（GSA）；multi-objective optimization；decomposition；multi-population strategy

TP18

：A

：0367-6234（2015）11-0069-07

10.11918／j.issn.0367-6234.2015.11.012

2014-11-30.

国家自然科学基金（61175126）；中央高校基本科研业务费专项资金（HEUCFZ1209）；高等学校博士学科点专项科研基金（20112304110009）.

毕晓君（1964—），女，教授，博士生导师.

毕晓君，398317196＠qq.com.