基于人工蜂群算法高光谱图像波段选择

王立国，赵 亮，刘丹凤

（哈尔滨工程大学信息与通信工程学院，150001哈尔滨）

基于人工蜂群算法高光谱图像波段选择

王立国，赵 亮，刘丹凤

（哈尔滨工程大学信息与通信工程学院，150001哈尔滨）

为减少高光谱遥感图像光谱空间冗余、降低计算复杂度，提出一种基于人工蜂群算法的高光谱图像波段选择方法.首先，根据波段相关性矩阵对全波段进行预处理，获得相关性较小的波段子空间；然后，利用人工蜂群算法以最佳指数与JM距离的加权和为适应度函数在各子空间进行邻域搜索，不断更新至收敛为止，从而获得最优波段组合.最后，利用AVIRIS数据和ROSIS数据对提出的算法与基于蚁群，粒子群，拟态物理学算法的波段选择方法进行实验.仿真结果表明：基于人工蜂群算法的波段选择能够在保证良好收敛性的同时，大大降低计算花费，所获得的波段组合用于高光谱图像分类时，可以得到较好的分类精度.

高光谱遥感；波段选择；人工蜂群算法；分类

高光谱遥感数据具有高维的特点，并且光谱空间各波段相关性大，冗余度高，在后续进行分类处理时会出现Hughes现象，而降维即可压缩数据，降低其存储空间也可减少计算复杂度，因此降维对高光谱遥感数据的后续处理具有重要意义.

波段选择作为一种直接的降维方法，主要依据光谱数据的特点选择合适的波段变量，在保留原始波段变量的物理意义以及光谱特性同时降低了数据维度，可以效地对高光谱图像降维［1］.根据是否有先验知识，高光谱图像波段选择方法可分为有监督波段选择和无监督波段选择［2］.由于有监督波段选择方法可对已知类别样本数据进行学习训练，因此通常能够取得更好的结果.

对于波段搜索方法，一般分为两种：最优搜索算法和次优搜索算法［3］.最优搜索算法实质是穷举法，对于具有高维特征的高光谱遥感数据穷举所有波段组合难以实现，因此实际中更多的是选择次优搜索算法.次优搜索算法是以准则函数为评价依据，通过特定的方法从波段组合中选择一组性能比较好，但不一定最好的特征组合.最简单的次优搜索策略采用序贯前向选择法和序贯后向选择方法，预先设置特征子集的数目，然后每次从当前的特征子集中加入或去除一个特征来获取最佳的特征子集［4］.

近年来，随着智能优化算法的发展，许多搜索算法也被用于降维，具有代表性的如遗传算法［5］、蚁群算法［6］、拟态物理学算法［7］等.从实验结果来看这类方法的效果要好于其他方法，为高光谱遥感图像波段选择研究提供新方向.虽然上述方法可以选择出较好的波段子集，但是收敛速度较慢，因此针对以上方法搜索时间较长的缺点提出一种基于人工蜂群的波段选择方法.人工蜂群算法［8］是一种新的群智能算法，以自然界中蜂群的自组织模型和群体智能为基础的一种仿生算法，它的主要特点是不需要预先知道问题的特殊信息，只需要对问题做质量评价，通过人工蜂的个体寻优，最后在群体中得到全局最优.经过大量标准函数测试实验表明，人工蜂群算法通过3种蜂群间的协作与角色转换，较好的缓解了搜索范围的扩展与在原搜索域进行精密搜索间的矛盾，在很大程度上避免了陷入局部最优的问题，另外其在搜索最优解的过程中采用了贪婪的搜索策略，相比其他非贪婪搜索算法，其收敛速度更快.因此本文提出了基于人工蜂群算法的波段选择算法，并通过实验验证其有效性.

1 波段选择过程描述

波段选择主要包括两个部分：波段选择的准则和搜索波段的算法.由于高光谱遥感图像具有相邻波段的光谱相关性强的特点，因此预先对波段进行子空间划分，得到相关性较弱的几个子空间，再在各个子空间内搜索需要数目的代表波段.而后利用搜索算法根据所选准择函数选择波段组合.

1.1 子空间划分

自动子空间划分的方法主要是根据波段相关系数矩阵图像分块特性及近邻可传递相关性来进行高光谱数据空间划分，步骤如下［9］：

1）将二维波段图像转换为一维的波段向量；

2）计算波段向量的相关系数得到高光谱数据的相关矩阵R，其定义为R=［r1，1，r1，2，…，rj，1；r2，1，r2，2，…，rj，2；…；rj，1，rj，2，…，rj，j］；

3）从相关矩阵中来提取近邻可传递相关矢量rNTR，其定义为rNTR=［r1，2，r2，3，…ri，i+1，…rj-2，j-1，rj-1，1］T，对近邻可传递相关矢量进行处理得到c-1个局部相关的极小值；

4）根据得到的c-1个极小值将高光谱数据空间划分c个适合的数据子空间．

经过划分后可以得到不同维度的子空间，每个子空间内的波段数据具有相近的光谱特性.

1.2 选择准则

选择方法一般依据各波段的信息量以及波段间的相关程度来选择有代表性的波段，通常选择信息量大、相关性较小的波段.因此兼顾信息量与相关系数的最佳指数OIF（optimum index factor）适合作为波段选择的选择准则：

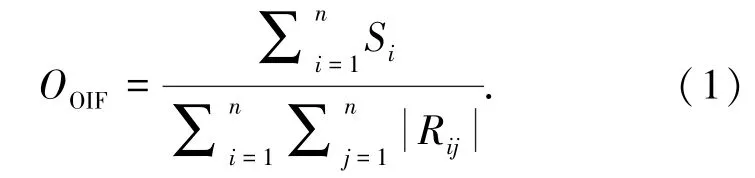
式中：Si是第i波段的标准差，n为波段数目，Rij为第i波段和第j波段的相关系数．同时，为使后续的分类效果更好，则加入衡量类别可分性的判据与OIF共同作为选择准则.鉴于JM（jeffries-matusita）距离兼顾数据的一阶和二阶统计量，且在高维数据空间二阶统计量对分类精度的提高非常重要，因此类别可分性判据选择JM距离［10］为

式中：μi、μj分别为第i、j类地物光谱均值矢量，Ci、Cj分别为第i、j类地物在任意波段组合上的协方差矩阵．

1.3 搜索算法

对于搜索算法，本文采用人工蜂群算法.人工蜂群算法与蚁群算法类似同属于群智能算法，是对蜜蜂采蜜行为进行分析从而模拟得到的算法.其关键要素有：蜜源，雇佣蜂（又称引领蜂）与非雇佣蜂.其中非雇佣蜂又分为：跟随蜂和侦察蜂.由这3种要素又产生3种行为模式，蜜源吸引蜜蜂，搜索蜜源，舍弃蜜源.算法的主要思想是：在随机产生的初始蜂群（其中蜜源与雇佣蜂是一一对应的）中，在收益度高的一半蜜源附近开始搜索，采用一对一的竞争生存策略择优保留个体，此过程为雇佣蜂搜索.然后利用轮盘赌选择方式选择较优个体，并在其周围进行贪婪搜索，产生另一半个体，这一过程称之为跟随蜂搜索.将引领蜂和跟随蜂产生个体组成新的种群，避免种群多样性丧失进行侦察蜂的类变异搜索，形成迭代种群.算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，向全局最优解靠近［8］.基于引言中介绍的人工蜂群算法的以上几个优点，本文将其用于搜索最佳波段组合.

2 基于人工蜂群算法的波段选择

2.1 蜜源初始化

2.1.1 蜜源的维数

本文提出的基于人工蜂群算法的波段选择中每只引领蜂所对应的蜜源代表着一种可能的波段组合.而蜜源的维数l，即等于波段组合中的波段数．对波段进行子空间划分后，得到n个相关性较低的子空间，因此解的形式有两种：1）每个子空间内各选l个波段，最后的波段组合内含有n个波段；2）按照各子空间内所包含波段数的比例来决定每个子空间所选的波段数

2.1.2 蜜源的位置与收益度

初始蜜源的位置按照式（4）随机生成，同时将进化代数置为0，NNP为蜜源个数分别为各波段子空间的上下边界.为第0代种群中的第i个蜜源，Rrand为［0，1］区间上的随机数．

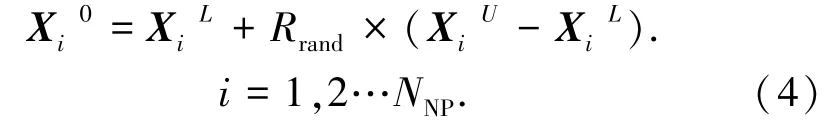
至此，蜜源可为一个NNP×l的矩阵，矩阵的每一行代表着一种波段组合策略.蜜源的收益度（适应度函数）则综合波段组合的信息量，相关度以及类别可分性，采用OIF及JM距离的加权和来衡量. OIF及JM距离均为数值越大越好.

2.2 蜜源的更新

按照2.1.2中方法计算第t代蜜源的收益度，将收益度较高一半蜜源对应雇佣蜂中的引领蜂，收益度较低的一半蜜源对应跟随蜂，然后引领蜂和跟随蜂各自进行搜索，更新蜜源位置，而蜜源的个数始终保持不变，为引领蜂和跟随蜂种群的个体的总和.

2.2.1 引领蜂搜索

式中：Rrand为（0，1）之间随机数，由于所得个体V的元素为波段序号，所以对邻域增量进行取整操作，如果每个个体的某一维在更新过程中，其数值超过子空间的范围则做如下处理.

2.2.2 跟随蜂搜索

引领蜂完成邻域搜索后，跟随蜂会依概率选择当前跟随蜂所对应的较优蜜源，完成采蜜.所依据的概率如式（7）所示，用轮盘赌的选择方式选出较优的引领蜂个体选择的个体按式（4）进行搜索，产生新的跟随蜂个体更新跟随蜂种群.

2.2.3 侦察蜂搜索

雇佣蜂完成搜索g（g＜G）次后，若有某一蜜源连续Llimit次不变，则相应雇佣蜂个体角色转为侦查蜂，按照式（4）产生新蜜源，计算新蜜源收益度，然后与原蜜源收益度比较，择优保留收益度高的蜜源.

2.3 基于人工蜂群算法的波段选择流程

基于人工蜂群算法的波段选择流程总结以下步骤：

步骤1初始化参数蜜源数目NNP、蜜源停留最大次数Llimit和迭代次数G，对波段空间进行子空间划分，按照式（4）随机生成NNP个l维蜜源，设置进化代数为t=0；

步骤2按式（2）、（3）计算各个蜜源的收益度，即当前各波段组合的OIF与JM距离的加权和；

步骤3对蜜源收益度按照从大到小进行排列，收益度高的前NNP／2对应引领蜂种群，后NNP／2对应跟随蜂种群；

步骤4计算新蜜源与原蜜源的收益度，择优贪婪选择蜜源，同时按照蜜源选择更新或保持引领蜂种群中的各个个体；

步骤5跟随蜂种群按式（7）依概率从步骤4新引领蜂种群所对应蜜源中选择，并按式（4）更新种群个体，依贪婪准则保留优质蜜源形成跟随蜂种群；

步骤6结合步骤5和6中个体构成迭代种群；

步骤7判断是否有蜜源连续Llimit次不变，若有则进行侦查蜂搜索，并按式（4）产生新蜜源.记录现有人工蜂群所搜索到的最优蜜源，即当前最佳波段组合.

步骤8令迭代次数t=t+1，若t＜G则转步骤3继续迭代至t=G，停止搜索，输出最优波段组合．

整个算法的流程见图1.

图1 ABC算法的操作流程

3 实验与分析

为验证本文算法的有效性与可行性，进行了仿真实验，同时与基于蚁群算法ACO（ant colony optimization），基于粒子群算法PSO（particle swarm optimization），以及基于拟态物理学算法APO（artificial physics optimization）的波段选择算法进行对比［6-7，11］.实验环境为AMD双核处理器，主频2.47 Hz，有效内存3 GB，开发环境为Matlab R2008a.

实验数据为AVIRIS印第安纳农林数据和ROSIS帕维亚大学数据.印第安纳农林数据大小为144×144，包含200个可用波段，剔除背景共包含16类地物，主要农作物是生长期的玉米和大豆，结合地面实际测量数据，其中7种地物样本量过少，对于该数据不具有代表性，因此选取另9种样本数目较多的代表性地物作为实验用地物.帕维亚大学数据大小为610×340，包含103个可用波段，剔除背景共包含9种地物.两种数据地物类型及数目如表1所示.印第安纳农林数据经过子空间划分后得到子空间为：（1～36）、（37～79）、（80～103）、（104～144）、（145～200），于每个子空间内各选择一个波段，获得相关性较低的5波段组合.帕维亚大学数据经过子空间划分得到子空间为：（1～73）、（74～84）、（84～103），于每个子空间内各选择一个波段，获得相关性较低的3波段组合.

表1 地物类别及数目

一般评价所选波段组合的优劣主要从地物可分性，波段相关性以及波段组合所包含的信息量来看，显然分类效果越好，波段冗余越小并且所呈现的信息量越大的波段组合是我们所需要的.而对于搜索算法来说，搜索效果与搜索时间是同时要兼顾的两方面，在保证效果的同时能让搜索时间最少是搜索的目标.因此为验证本文波段选择算法的性能，从搜索效果和时间两个方面来评价各搜索算法.在搜索效果中，用波段间的平均相关性作为相关性衡量标准，其值越小越好；信息量采用OIF衡量，其值越大越好；分类性能采用总体分类精度OA（overall accuracy）衡量，其值越大表示分类正确率越高；而搜索时间为实际算法运行时间.其中平均相关性R与总体分类精度AOA为

式中：mii第i类测试样本被正确分类的样本数，c为样本类别数，C为样本总数，Rij为波段i和波段j的相关系数

3.1 搜索效果的比较

人工蜂群算法实验参数设置为：种群规模NNP= 30，迭代次数为30次，蜜源停留最大限制次数Llimit=5．其他算法的参数设置参考文献［7，12］.分类方法为最大似然法，两种数据分别取3、5、9类地物进行比较，其训练样本和测试样本均为各取50%.并且在实验中所得到的平均相关性、OIF，分类精度均为20次实验结果的均值.将4种算法的结果对比列于表2、3.

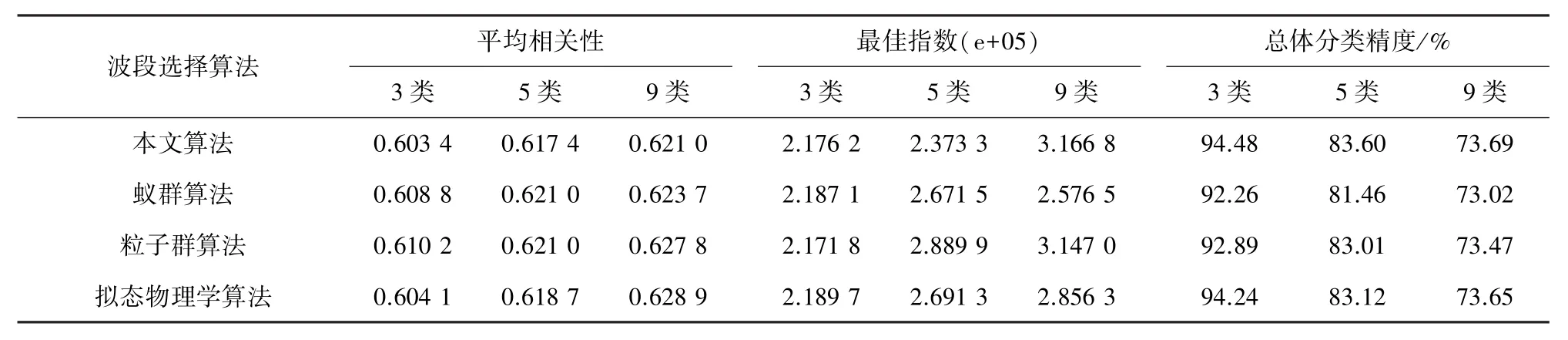
表2 4种算法搜索效果对比（印第安纳数据）

表3 4种算法搜索效果对比（帕维亚大学数据）

从表中数据可看出本文算法与基于蚁群算法的波段选择方法相较，无论在信息量还是分类精度上均占优，这是由于蚁群算法信息素更新能力有限，算法容易陷入局部最优，从而出现停滞现象；当问题规模增大时，算法效率明显下降；与基于粒子群算法波段选择算法相比，基于人工蜂群算法的波段选择虽然在信息量方面较其略低，但分类精度要高于该算法，因为本文在判决准则中加入衡量类别可分性的JM距离，使搜索到的波段更利于分类处理；而对于基于拟态物理学算法的波段选择算法相较，在信息量与分类精度上二者相当.

为更直观地体现分类效果，将实验所用的9种地物真实分布图及各种算法分类最好结果示于图2～7.

图2 印第安纳数据3种类别分类结果

图3 印第安纳数据5种类别分类结果

图4 印第安纳数据9种类别分类结果

图5 帕维亚大学数据3种类别分类结果

图6 帕维亚大学数据5种类别分类结果

图7 帕维亚大学数据9种类别分类结果

3.2 搜索效率的比较

搜索效率的评价为各算法收敛时所用的时间，将其列于表4.从表中数据可看出基于人工蜂群算法的波段选择所用时间远低于其他算法.体现出人工蜂群算法收敛速度快的优点.

综上两方面可以看出，本文算法在搜索结果上与APO算法相当，但优于ACO算法及ACO算法，而在搜索效率上，本文算法有明显优势，因此本文算法更适用于高光谱遥感图像波段选择.

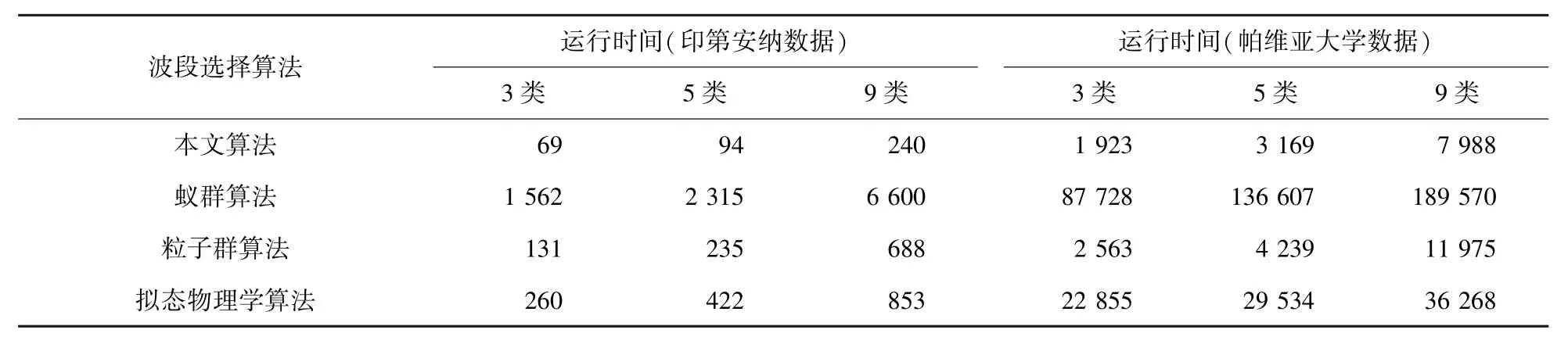
表4 4种算法所用时间

4 结 语

本文针对高光谱图像波段冗余问题，提出了基于ABC算法的波段选择算法，该算法具有设置参数少、收敛速度快的特点.与基于APO算法、基于PSO算法、基于ACO算法的波段选择方法进行了对比实验，仿真结果表明基于ABC算法的波段选择方法较其他3种智能优化算法在保证分类精度的情况下收敛速度更快，更加能够满足实际需求.

［1］GUYOU I，ELISSEEFF A.An introduction to variable and feature selection［J］.Journal of Machine Learning Research，2003，3：1157-1182.

［2］刘雪松，葛亮，王斌，等.基于最大信息量的高光谱遥感图像无监督波段选择方法［J］.红外与毫米波学报，2012，31（2）：166-171.

［3］周爽，张钧萍，苏宝库.基于最速上升算法的超光谱图像波段选择搜索算法［J］.计算机应用研究，2008，25（11）：3501-3503.

［4］SERPICO SB，BRUZZONE L.A new search algorithm for feature selection in hyperspectral remote sensing images［J］.IEEE Trans Geoscience and Remote Sensing，2001，39（7）：1360-1367.

［5］赵冬，赵光恒.基于改进遗传算法的高光谱图像波段选择［J］.中国科学院研究生院学报，2009，26（6）：795-802.

［6］周爽.蚁群算法在高光谱图像降维和分类中的应用研究［D］.哈尔滨：哈尔滨工业大学，2010.

［7］王立国，魏芳洁.APO算法的高光谱图像波段选择［J］.哈尔滨工业大学学报，2013，45（9）：100-106.

［8］KARABOGA D，BASTURK B.On the performance of artificial bee colony（ABC）algorithm［J］.Applied Soft Computing，2008，8（1）：687-697.

［9］刘颖，谷延锋，张晔，等.一种高光谱图像波段选择的快速混合搜索算法［J］.光学技术，2007，33（2）：258-261，265.

［10］张莲蓬，李行，陶秋香.高光谱遥感影响特征提取与分类［M］.北京：测绘出版社，2012.

［11］丁胜，袁修孝，陈黎.粒子群优化算法用于高光谱遥感影像分类的自动波段选择［J］.测绘学报，2010，39（3）：257-263.

［12］毕晓君.信息智能处理技术［M］.北京：电子工业出版社，2010.

（编辑苗秀芝）

Artificial bee colony algorithm-based band selection for hyperspectral imagery

WANG Liguo，ZHAO Liang，LIU Danfeng
（College of Information and Communications Engineering，Harbin Engineering University，150001 Harbin，China）

A hyperspectral image band selection algorithm based on artificial bee colony algorithm isproposed to reducespectralredundancy of hyperspectral remote sensing image and computational complexity.Firstly，accordingtothecorrelationcoefficientmatrices among bands some pretreatments have been taken too btain the band sub space with less relevance.Then，neighborhood search has been implemented on each sub-space by using artificial bee colony algorithm together with the weighted sum between JM distance and OIF as the fitness function.To obtain the optimal band combination，the search is updated until the algorithm is convergent.Finally，the proposed algorithmis used to compare with band selection methods based on ACO，PSO and APO.The experimental results show that the proposed algorithm can not only ensure a good convergence but also reduce the computational cost. Simultaneously，when the obtained bands combination is used for hyperspectral image classification，higher classification accuracy can be obtained.

hyperspectral images；band selection；artificial bee colony algorithm；classification

TN911.73

：A

：0367-6234（2015）11-0082-07

10.11918／j.issn.0367-6234.2015.11.014

2014-09-09.

国家自然科学基金（61275010）；国家教育部博士点基金（20132304110007）；黑龙江省自然科学基金（F201409）；中央高校基本科研业务费重点项（HEUCFD1410）.

王立国（1974—），男，教授，博士生导师.

王立国，wangliguo＠hrbeu.edu.cn.