基于遗传-模拟退火算法的空间目标地基监视调度方法

2015-06-05鄢青青沈怀荣邵琼玲

系统工程与电子技术 2015年12期

关键词：测站算例调度

鄢青青，沈怀荣，邵琼玲

（1.装备学院研究生管理大队，北京101416；2.装备学院航天装备系，北京101416）

基于遗传-模拟退火算法的空间目标地基监视调度方法

鄢青青1，沈怀荣2，邵琼玲2

（1.装备学院研究生管理大队，北京101416；2.装备学院航天装备系，北京101416）

空间目标监视是航天任务得以顺利开展的重要基础。针对空间目标地基监视中的大规模复杂调度问题，建立了包含多种约束条件和优化目标的调度问题数学模型。探讨了利用遗传算法对全局解的一部分进行局部优化以提高资源利用率的算法混合策略，构建了遗传模拟退火算法，其中对模糊需求使用了启发式方法以构造可行解的局部，并采用窗口修剪法进行冲突处理。仿真结果表明，遗传模拟退火算法与窗口修剪法结合能够在可接受的时间内求得满意的解，验证了模型和算法的有效性。

空间监视；优化调度；模拟退火算法；遗传算法

0 引言

空间目标监视是航天任务得以顺利开展的重要基础。20世纪90年代以前，人们主要通过计算机辅助的人工调度方法来解决空间监视网（space surveillance network，SSN）中的任务安排或资源分配问题［1］。但随着外层空间里需要关注的空间目标数目不断增加，和人们航天活动的日益频繁，以及对空间目标监视资源调度的质量要求越来越高，人工调度已不能满足需求。而基于任务规划、资源调度和优化方法的自动_调度方法在增加监视网编目目标数目、提高资源利用率、提高重点关注目标的综合编目精度等方面，具有明显优势，能够满足更多数量和类型的航天任务对空间监视的需求。1993年MITRE公司开发了一款基于贪婪算法和传感器权重的自动传感器规划程序Prototype Tasker［1］，1994年文献［2］使用模拟退火（simulated annealing，SA）算法优化了传感器权重的选择过程。美国空间控制中心（space control center，SCC）在空间监视网资源分配中正在使用的是第二代自动任务分配系统［3-4］，该系统将SSN传感器任务规划问题描述为经典多资源分配问题，采用边际分析法（marginal analysis）对其进行分析和求解，并在实际应用中与第一代系统进行了对比，表明其在平衡目标的跟踪需求与SSN的跟踪能力上的表现更优秀。另外，文献［5］提出用多传感器互补式观测的方法提高目标编目定轨精度。文献［6］采用数据驱动的方法来离散搜索空间以实现快速搜索，并采用基于约束的调度算法最大化调度的跟踪次数。文献［7］基于在线应用STK Scheduler Online，提出了提高定轨精度和地面资产利用效率的SSA（space situational awareness）传感器任务规划方法。文献［8］提出基于费希尔信息矩阵的ad-hoc改进规划算法。文献［9］专门研究了基于同步观测的传感器组合以提高轨道估计精度的调度方法。中国的学者也分别用贪婪算法［10］、随机搜索算法［11］、线性规划方法［12］等对空间目标监视的单站和全网资源调度进行了研究。以上这些研究有的以监视网的历史数据为基础进行局部重调度，有的仅考虑了空间目标的编目任务或单一的调度优化目标，有的则仅考虑了单个测站的资源调度问题，为了更接近空间目标地基监视调度的实际情况，需要对全网监视资源在多任务、多优化目标和复杂约束情况下的调度问题进行研究。

为此，本文首先基于对空间目标地基监视调度问题中各要素的分析，建立了包含多任务、多优化目标和复杂约束条件的调度问题模型；根据不同监视任务类型对监视时间窗口的要求，设计了多种可行解构造方法；并根据SA算法的收敛速度快和不依赖初始值等优点［13］，将其与遗传算法（genetic algorithm，GA）结合，利用遗传算法寻优能力更强的特点对可行解的局部进行优化，以提升资源更加紧张的部分空间目标（空间目标）的调度效果；结合提出的一种窗口修剪冲突处理方法，以获得更多被成功调度的空间目标；最后，通过仿真计算验证了本文所用方法有效性。

1 调度问题的分析与建模

1.1 问题分析

空间目标的地基监视调度，是在满足监视任务需求和约束条件的基础上，优化分配地面观测资源及其时间资源，以实现更好地监视空间目标为调度目标的过程，该问题的描述中至少应该包含5个要素，即地面观测资源集、空间目标集、监视任务集、约束条件集以及调度优化目标。

其中，地面观测资源是指以雷达天线或光学望远镜为代表的空间目标信息获取和处理设备，包括其备份资源。空间目标是指离地面高度150 km以上的所有人造或自然天体，空间目标监视的对象目前限定为离地40 000 km以内的各类航天器、导弹、箭体、空间碎片等物体。空间目标监视任务是指由空间目标监视网的管理者或使用者提出，在一定时间范围内执行的，对一个或多个目标进行的特定监视活动，主要包括空域搜索和跟踪测量两种监视方式，且该监视活动需满足任务提出的观测条件、数据类型、观测资源范围等约束和要求，如航天器碰撞预警与规避、航天器故障处理、航天发射等活动中的支持监视任务，及潜在威胁目标动向监视预警、空间目标轨道信息编目等专门监视任务。

另外，在空间目标监视中，跟踪是指在观测资源与空间目标的一个相互几何可见的时间窗口内进行的多次观测。而一次观测是观测资源对空间目标的一次定点测量，输出一组与轨道参数、图像、物理特性等相关的测量数据。空域搜索则是使用搜索设备（如相控阵雷达、搜索望远镜）对特定空域进行的扫描式重复探测，以发现新目标、查找失跟目标等。

1.2 问题建模

根据上述分析，用一个5元组表示空间目标地基监视调度问题：｛S，O，M，C，T｝，其中S＝｛sj；j∈［1，M］｝表示地面观测资源集合；O＝｛oi；i∈［1，N］｝表示需监视的空间目标集合；M＝｛ml；l∈［1，NM］｝表示监视任务集合；C表示约束条件集合；T表示调度优化目标。

考虑调度成功的目标数目最多、观测质量最高、综合优先级最高3个调度目标，则目标函数为

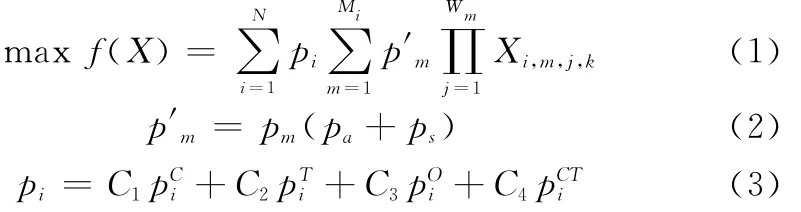
式中，Xi，m，j，k是0－1型决策变量，表示当前解中，第i个目标的属于第m个计划任务的第j个跟踪时间窗口是否被当前解接受，这个跟踪时间窗口由第k个地面观测资源执行。p′m表示第i个目标所属第m个计划任务的优先级；pm为任务m指定优先级；pa为该任务中目标i的观测质量（对定轨精度的影响）评价值；ps为该目标所用资源的优先级之和；pi为目标i的优先级，根据目标的“合作／非合作”特性、目标类型、轨道类型、产生时间4个因素综合评价产生。由于合作目标一般由航天测控网中的合作测量资源观测，因此在空间目标监视中给予较低优先级，以节省更多观测资源用于观测非合作目标；空间目标主要有有效载荷、箭体、碎片3类，其优先级由高到低；轨道分类采用改进的Kaman分类［14］，包含97.252 4%的空间目标，由于高轨和低轨采用不同的观测资源，因此在低轨目标（1～4类）中，轨道高度越低的目标由于大气阻力摄动影响，其轨道变化率越大，也就具有更高的优先级，高轨目标（5～7类）中，轨道高度越低的目标具有更少的可见时间，因此也具有更高的优先级；产生时间越晚的目标，其轨道和状态发生变化的概率越大，因此具有更高的优先级。

问题中的约束条件如下：

（1）可见性约束，即跟踪时间窗口必须在几何可见时间窗口之内，且对光学观测而言，观测时光学设备必须在地影内、空间目标必须在阳光照射下：

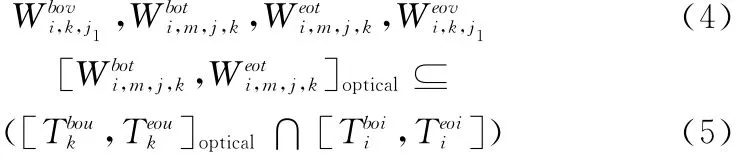
（2）观测资源工作时段、作用范围、输出数据类型、同时可跟踪目标数目约束：

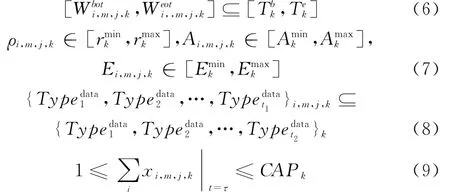
（3）任务要求执行时段、观测条件（最低观测仰角、最短跟踪时间窗口、最大采样间隔）约束：

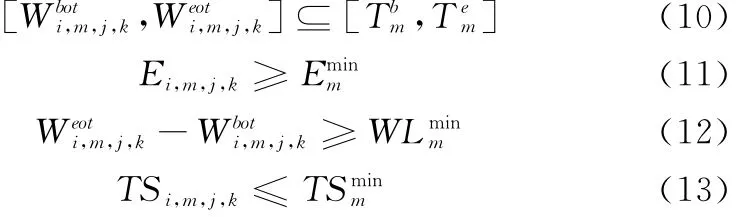
（4）任务观测需求约束，是任务提出的对某个目标的观测总时长、窗口数目及在资源、时间上的分布、偏好的观测资源范围等约束条件，是在调度过程中构造可行解的主要依据。

（5）优先级约束，是多个对象之间相对重要程度的量化表示，并且优先级高的在被选择的过程中具有更高的优先权或被选中概率。优先级可以人为指定或根据相关知识计算，一般来说，人为指定的优先级不可更改。优先级约束是冲突处理的主要依据。本调度问题中，空间目标、任务、观测资源中均存在优先级约束，必要时还可根据信噪比（雷达探测）或探测概率（光学探测）来计算跟踪时间窗口的优先级。

2 基于GA- SA的求解算法

2.1 求解算法

SA算法思想最早由Metropolis等提出，并由Kirkpatrick在1983年应用于组合优化中［15］。它通过解构造和降温条件判断的自适应迭代过程，并结合Metropolis准则以跳出局部最优，在解空间中概率性地搜索全局最优解。SA算法具有鲁棒性强、简单通用、不依赖初始解、适于并行处理等优点，适合在大规模的调度问题中快速获得次优或满意的全局解［16］。

空间目标地基监视调度问题属于大规模调度问题，为保证调度算法的时间性能，本文采用SA算法进行全局优化求解。同时，针对深空目标所能利用的光学传感器资源比较稀少的问题，利用GA对深空目标所对应的部分解进行局部优化，以在不对全局收敛速度产生较大影响的情况下，更加充分地利用光学传感器资源完成对深空目标的数目最大化地监视。

步骤1初始化，给定初始温度T0、Metropolis链长L、降温速率q、初始种群S1，并对S1进行冲突处理和计算种群中最大目标函数值max（f（S1））。其中初始种群S1构造时，首先对所有深空目标构造NGA个不同的部分解，再对所有近地目标构造一个部分解，并将后者复制NGA份与前者组成NGA个全局可行解，即种群大小为NGA。

步骤2 对每一温度T及k∈［1，L］，循环进行步骤3～步骤7。

步骤3 产生一个新种群S2。在近地目标的部分解重构中，对种群S1每个个体中经冲突处理后成功保留下来的解单元（即每个空间目标对应的所有窗口的集合）按概率Pg重构，对没有成功调度的解单元全部重构。而将种群S1经冲突处理后的深空目标部分解取出构成子种群S′1，对其进行选择（Ps）、交叉（Pc）、变异（Pm）操作，得到新的子种群S′2，并将其与近地部分解重构为新的种群S2。

步骤4 对S2中每个可行解的所有跟踪时间窗口进行冲突检测和处理，计算S2中每个解的目标函数值，并取最大值max（f（S2）），计算目标函数增量Δf＝max（f（S2））－max（f（S1））。

步骤5 由于目标函数表示为最大化问题，因此如果Δf＞0或e（Δf／T）＞rand，则接受新种群S2为当前种群S1。

步骤6 判断迭代终止条件，如达到最大迭代次数或连续若干次未更新当前种群。

步骤7 降低温度控制参数T，并判断是否达到设定终止温度Tend，否则转步骤2。

2.2 可行解的构造方法

本文假设4类计划监视任务，分别为：①在任务时段内需安排尽量多的非重叠监视时间的支持类监视任务；②在任务时段内需重点监视（高精度、给定“跟踪次数／测站数”需求）的专门监视任务；③维护空间目标编目信息库所需的日常编目监视任务；④空域搜索任务。

每个空间目标对应的所有窗口组成解的一个单元，全局可行解由所有空间目标的解单元构成。在解单元构造时，对每个空间目标所对应的不同监视任务进行不同的解单元的子单元构造，再对这些子单元进行同时段合并（同一时段内的窗口或窗口部分，保留优先级最高的窗口），避免不必要的多个资源对同一目标进行跟踪的情况，提高资源利用率。

2.2.1 支持监视任务

这里设定支持监视任务的跟踪要求为在任务时段内获得一组重叠尽量少、监视总时长尽量长的跟踪窗口，可将这个任务需求视为一个优化问题，采用启发式方法来求解。该优化问题可描述为：选取一组时间窗口，该组时间窗口构成的总时间窗口完全或最大限度覆盖整个任务时间段，并使这些时间窗口的重叠程度最小。

目标函数：

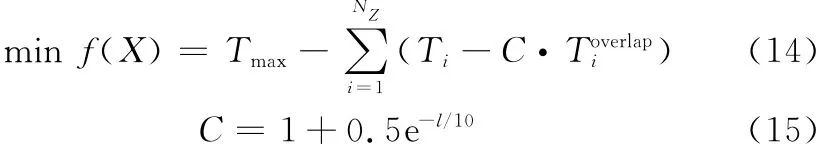
式中，Tmax为任务时段长度；为构成窗口集（即解单元的子单元）的第i个时间窗口的时长，为该窗口与前i－1个已被接受的窗口所构成的窗口集合的重叠时长（见图1）；NZ为该目标该监视任务的所有备选窗口数目；C为系数，随迭代次数l增加呈指数下降，以在算法运行早期提高解质量，后期加快收敛速度。

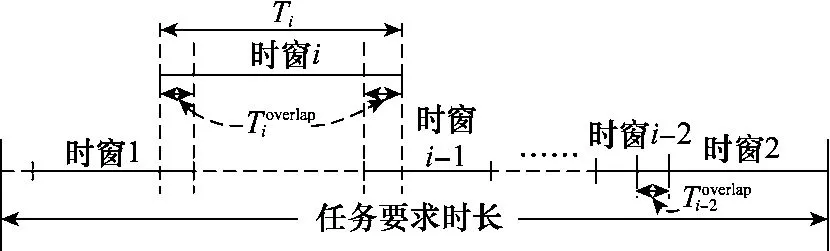
图1 第i个时间窗口与当前时间窗口集合的关系示意

这是一个无约束优化问题，采用基于概率禁忌表和贪婪准则的启发式方法产生满足某目标某计划任务观测跟踪需求的一组时间窗口。具体算法步骤如下：

步骤1初始化：初始化最大迭代次数CTmax；初始化每次迭代时的寻优计算次数L；初始化迭代终止条件中的连续无新解被接受次数M；窗口集合总时长TN初始化为0；随机选择一个时间窗口作为初始值，计算f（X），将该窗口移入路径记录和禁忌表中。

步骤2 在备选窗口集合中随机选取L个窗口，分别计算目标函数和其增量Δfj＝fj－fi－1，j∈［1，L］。

步骤3 选出使Δf最大的窗口，如果Δf＞0，则接受该窗口作为构造解的一部分，记录该窗口到路径中，更新f（X），其余个窗口分别以概率pj＝／Tj，j∈［1，L－1］移入禁忌表，并置M为零；如果Δf≤0，则将这L个窗口分别以概率移入禁忌表，并更新M。

步骤4 更新迭代次数CT，目标函数系数C，构建窗口集合总时长TN（重叠部分只计一次）。

步骤5 判断是否符合算法终止条件，即构建窗口总时长等于任务要求总时长，或M达到规定值，或迭代次数达到终止条件。

以一个算例验证该局部优化方法的有效性：选择空间目标TLE-25544，即国际空间站（ISS），作为第1种任务（在轨操作／维修支持）的监视对象，监视资源采用SSN中的23个测站［3］，任务持续时间为“8 Jan 2014 16∶20∶00.000～8 Jan 2014 17∶20∶00.000”，时长60 min，最大迭代次数为50次，M取为5次，L为2。最终获得5个不同测站的5个时间窗口，总共约35.9 min的有重叠监视时间（34.6 min的不重叠时间），其目标函数进化曲线和时间窗口分布如图2所示。

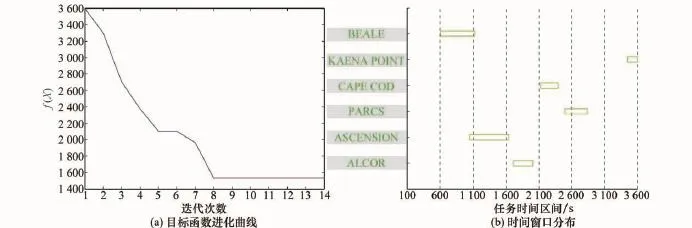
图2 空间目标TLE-25544的支持监视任务时间窗口组合优化结果

2.2.2 重点监视任务

假设重点监视根据定轨精度的不同，按经验形成了一个监视需求查询表。首先通过查询或计算得到针对该目标的重点监视，当天应该跟踪的次数与使用的测站数，即“T／S”（Tracks／Stations）。然后采取如下方法，从某目标、某任务的备选可见时间窗口中选择并组合窗口以满足跟踪需求。

（1）对深空目标（平均高度＞5 700 km）

①选择测站。从备选可见窗口的所属测站中随机选择S个独立测站，如果备选独立测站数小于S，则直接全选所有测站。

②规划每个测站的跟踪次数。先至少保证每个测站一次跟踪，然后将剩余T－S次跟踪随机分配给所有测站。

（2）对低轨目标（平均高度＜2 500 km）

①选择测站。方法同上。保证所选测站的备选可见窗口数目总和大于等于需求的跟踪次数T。

② 规划每个测站的跟踪次数。方法同上。

③ 选择或截取跟踪时间窗口。如采用跟踪窗口与可见窗口等长方式，则直接为每个测站每次跟踪，随机选择符合观测条件的备用可见窗口。如采用不等长方式，则从随机选择的备用可见窗口中截取符合观测条件的跟踪时间窗口。

④特性测量需求满足。方法同上。

2.2.3 其他任务

对编目监视任务，参考文献［14］，按Kaman轨道分类，第1类和第4类为每天跟踪一次，第2类为每2天跟踪一次，第3类为每3天跟踪一次，第5～7类为每7天跟踪一次，每次跟踪应保证跟踪时间窗口长度大于2 min。对空域搜索任务，直接为其分配要求时长的搜索时间窗口。

2.3 冲突处理方法

冲突是指两个同一资源的两个跟踪时间窗口存在重叠部分，或窗口之间的间隔时间小于该资源的状态转换时间。对同一观测资源，同时有超过观测资源最大同时可观测目标数的空间目标要求进行观测，即会产生冲突。一般而言，机械扫描雷达只能同时跟踪一个目标，相控阵雷达可同时跟踪多至上百个目标，光学望远镜则只能观测同时出现在视场内的部分目标。

冲突处理即是在出现冲突的两个或多个跟踪时间窗口之间进行抉择以消除冲突。这里采用两种冲突处理方法，即选择／放弃法、窗口长度修剪法。选择／放弃法是根据对每个窗口的优先级评价，在冲突的窗口中选择要保留的窗口或删除要放弃的窗口。窗口长度修剪法是根据窗口优先级，对冲突的窗口中优先级较小的窗口的冲突部分进行修剪，留下无冲突且大于最小跟踪窗口长度的部分。

冲突处理的步骤是，将当前解中的所有时间窗口按所属观测资源进行集中；对每一集合中的每一窗口检测其与其他所有窗口是否冲突，并记录冲突信息（如两两冲突状态、冲突时间区间）；评价所有窗口的优先级；按冲突次数和优先级，对每个窗口进行逐个冲突处理和更新冲突信息。

3 算例仿真分析

3.1 仿真算例

目前，全世界只有美国和俄罗斯具有日常更新空间目标监视编目信息的能力。这里，以美国的SSN中的23个测站［3］作为仿真用的空间目标监视网，包括17个雷达测站和6个光学测站，且规定其中有多个传感器资源的测站只能同时使用一个测站，其余作为备份。机械雷达转换时间为5 min，光学传感器转换时间为10 s。另假设在空间目标监视网中，专用传感器资源每天24小时均能参与监视，兼用传感器资源每天可提供随机产生的连续12小时监视时间，可用传感器资源每天可提供随机产生的连续6小时监视时间。

空间目标轨道参数采用2014年1月7日的TLE数据，包括8 146个独立的空间目标，其中深空目标1 523个，近地目标6 623个。

为了便于比较和分析，本文设计了两个算例，场景时间均为2014年1月8日08∶00至1月9日08∶00，采用GA-SA算法和SA算法，每种算法中分别用两种冲突处理方法处理时间窗口冲突。

算例1 设置6个计划监视任务：包括支持监视任务3个、重点监视任务1个、编目监视任务1个、空域搜索任务1个；任务优先级由高到低分别为10、9、8、6、2、1；任务执行时间为18∶00－20∶30、16∶20－17∶20、10∶00－12∶00、8日08∶00－9日08∶00、8日08∶00－9日08∶00、11∶00－11∶30；分别随机加入监视空间目标，其数目为7、3、3、163、8146，空域搜索设定搜索空域；重点监视任务监视需求统一设为“4／2”；其中支持监视任务和重点监视任务限制了可用资源范围、包含的监视目标、要求的数据类型和跟踪条件等。编目监视任务给出两种目标数目，一是根据第2.2.3小节的方法随机产生的目标数（加上其他任务要求的目标共约独立目标3 500个），二是使用全部8 146个目标。

算例2 仅设置一个编目监视任务，参数同算例1，目标数目也为根据第2.2.3小节的方法随机产生的目标数和全部目标。

仿真验证实验系统配置为Intel（R）Core i5-4440 CPU＠3.10GHz×4，Windows 7（64位），采用Matlab软件实现。GA-SA和SA两种算法参数设置如表1所示。

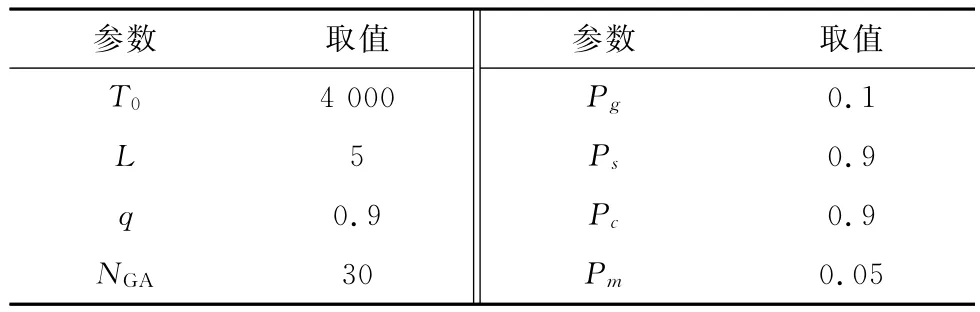
表1 算法参数设置

3.2 计算结果分析

图3为算例1的仿真结果，由图中可以看出，当有6个计划任务时，即使在成功被调度的空间目标数目相当或更少的情况下，GA-SA算法和窗口修剪法在获得的目标函数值上，均比同等条件下SA算法和窗口删除法表现更好。再通过对表2中的结果的分析，表明GA-SA算法和窗口修剪法能够成功调度更多的高优先级任务中的空间目标。

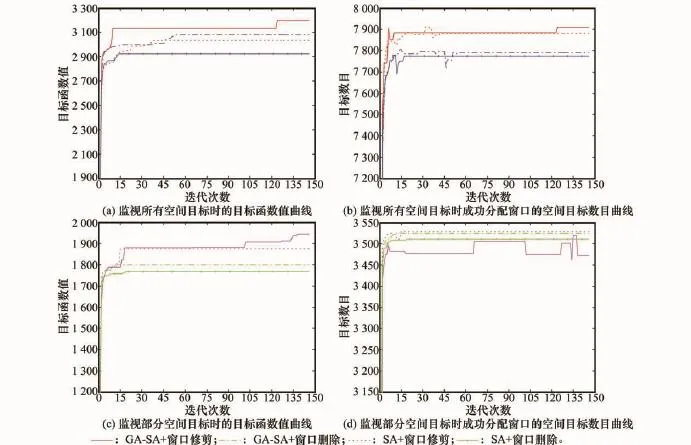
图3 算例1（共有6个计划任务）仿真结果

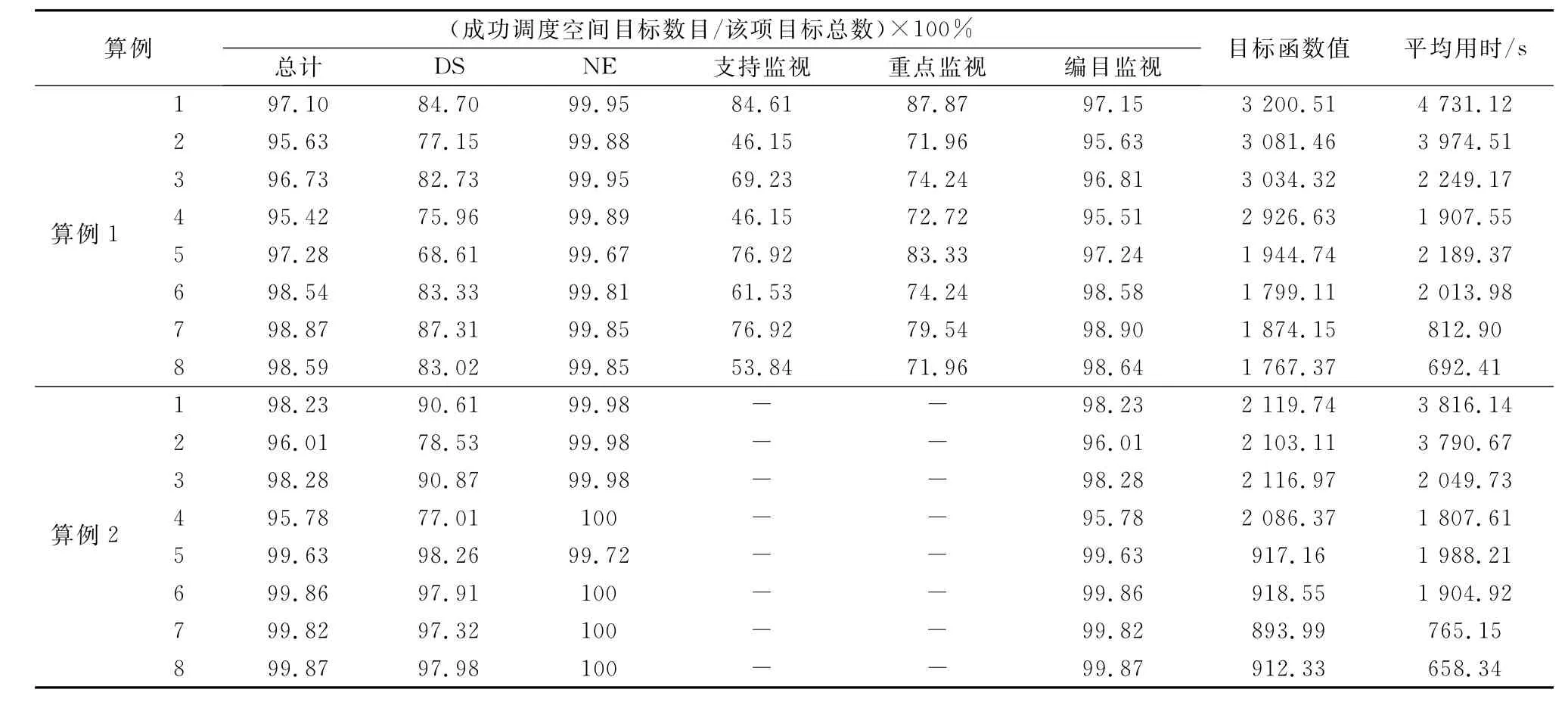
表2 算例仿真结果

图4为算例2（仅有编目任务）的仿真结果，由图中可以看出，当需要监视的空间目标数目较多时，在目标函数值和成功调度的空间目标数目上，窗口修剪法均比窗口删除法表现好得多，但GA-SA算法相对SA算法优势不太明显。而当需要监视的空间目标数目较少时，GA-SA算法相对SA算法在获得的目标函数值上表现较好，但成功调度的空间目标数目差别较小。结合表2中的数据可知，当需要监视的空间目标数目较多、资源较为紧张时，窗口修剪法可以使更多的空间目标被调度成功，从而也保证了得到更大的目标函数值，此时被成功调度的目标数目是目标函数值的主要影响因素；而当需要监视的空间目标数目较少、资源较为富余时，窗口修剪法不再有优势，但GA-SA算法仍然可以通过局部寻优来获得更大的目标函数值，且与窗口修剪法结合使用后效果更好。

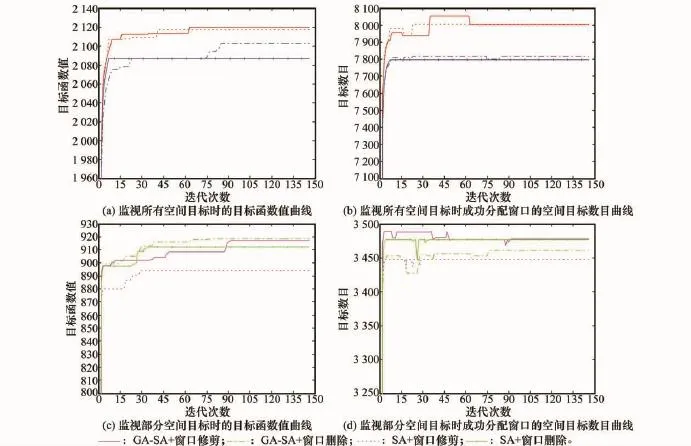
图4 算例2（仅有编目任务）仿真结果

由于支持监视任务和重点监视任务具有较高的优先级，因此在算例1的计算结果中可能出现调度成功的空间目标数目更多而目标函数值更小的情况，这也是算例1中的调度成功的深空目标数目普遍比算例2中少的原因。由于在算例设定时，支持监视任务和重点监视任务中的目标都是随机选择的，并没有考虑其在任务时段内是否有足够的可用时间窗口，因此造成了这两个任务的调度成功空间目标数目始终不足90%。经计算，算例1的第一条结果中这两种任务的成功目标数目占比基本达到任务中拥有足够可见窗口的空间目标数目的最大比例。从计算结果可以看出，由于对深空目标进行探测的传感器可用资源较少、且每个传感器资源可同时探测的目标数目太少，导致深空目标探测在加入更多任务、更多目标时，能够被成功探测的目标数目无法完全满足设计算例的跟踪需求。由于问题规模较大，表2中的算法运行时间可以认为在可接受范围内，当在实际应用中进入周期性重调度后利用历史经验数据即可大幅减少算法运行时间；且算法运行采用了并行计算的方式，运行平台的增强也有助于算法计算效率的提高。

4 结论

空间目标地基监视调度问题是一个多任务、多优化目标、多约束，且存在大量时间窗口冲突的复杂问题。通过对该问题基本要素的分析，建立了该问题的数学模型，并设计了遗传-模拟退火算法进行求解。经过使用GA-SA和SA两种算法、及两种不同冲突处理方法在两个算例中的计算表明，本文所提出的GA-SA算法和窗口修剪冲突处理方法在不同任务数目、不同空间目标数量规模下，均具有较好的调度性能，说明了本文提出的方法在解决空间目标地基监视调度问题过程中是合理、有效的。另外，本文在建立模型和设计算例的时候做的很多假设并不符合空间目标监视调度的真实情况，因此今后的努力方向应是结合更多空间目标监视的实际情况来研究高效的调度方法。

［1］Cherry P R.Sensor tasking by the space defense operations center［C］∥Proc.of the Space Surveillance Workshop，1993：93- 98.

［2］Petrick B L.Weighting scheme for the space surveillance network automated tasker［D］.Ohio，USA：Air Force Institute of Tech Wright-Patterson AFB OH School of Engineering，1994.

［3］Berger J M，Moles J B，Wilsey D G.An analysis of USSPACECOM’s space surveillance network（ssn）sensor tasking methodology［D］.Ohio，USA：Air Force Institute of Technology Wright-Patterson AFB OH School of Engineering，1992.

［4］Miller J G G.A new sensor allocation algorithm for the space surveillance network［J］.Military Operations Research，2007，12（1）：57- 70.

［5］Stottler R，Thompson R.Globally optimized scheduling for space object tracking［C］∥Proc.of the Infotech＠Aerospace Conference，2011：1- 8.

［6］Mohammed J L，Stottler D.Rapid scheduling of multi-tracking sensors for a responsive satellite surveillance network［C］∥Proc.of the Infotech＠Aerospace Conference，2010：1- 12.

［7］Herz A F，Stoner F，Hall R，et al.SSA sensor tasking approach for improved orbit determination accuracies and more efficient use of ground assets［C］∥Proc.of the Advanced Maui Optical and Space Surveillance Technologies Conference，2013：1- 10.

［8］Erwin R S，Albuquerque P，Jayaweera S K，et al.Dynamic sensor tasking for space situational awareness［C］∥Proc.of the A-merican Control Conference，2010：1153- 1158.

［9］Hobson T A，Clarkson I V L.Collaborative sensor scheduling for space situational awareness［C］∥Proc.of the Statistical Signal Processing Workshop，2012：640- 643.

［10］Xu Z C，Huang Y X.A scheduling method for cataloging observation tasks based on greedy algorithm［J］.Journal of Spacecraft TT&C Technology，2012，31（1）：89- 94.（徐忠超，黄永宣.基于贪婪算法的空间编目观测任务调度方法［J］.飞行器测控学报，2012，31（1）：89- 94.）

［11］Liang H，Niu W.Design and implementation of measurement resource scheduling for space object catalog［J］.Journal of Spacecraft TT&C Technology，2012，31（1）：84- 88.（梁华，牛威.空间目标编目测量资源调度策略设计与实现［J］.飞行器测控学报，2012，31（1）：84- 88.）

［12］Wang X.Scheduling strategy for electro-optical tracking of space objects［J］.Journal of Spacecraft TT&C Technology，2013，32（1）：89- 94.（王歆.空间目标光电跟踪的调度策略［J］.飞行器测控学报，2013，32（1）：89- 94.）

［13］Sun Y S，Li Y M，Zhang Y H，et al.Improved simulated annealing algorithm and its application in adjusting of S plane parameters in AUV motion control［J］.Acta Armamentarii，2013，34（11）：1418- 1423.（孙玉山，李岳明，张英浩，等.改进的模拟退火算法在水下机器人S面运动控制参数优化中的应用［J］.兵工学报，2013，34（11）：1418- 1423.）

［14］Barker W N，Casali SJ，Wallner R N.The accuracy of general perturbations and semianalvtic satellite ephemeris theories［C］∥Proc.of the AAS／AIAA Astrodynamics Conference，1995：1967- 1985.

［15］Kirkpatrick S，Jr D G，Vecchi M P.Optimization by simmulated annealing.［J］.Science，1983，42（3）：671- 680.

［16］Liang X，Huang M.The modern intelligent optimization algorithm and its application［M］.Beijing：Publishing House of E-lectronics Industry，2012：107- 113.（梁旭，黄明.现代智能优化混合算法及其应用［M］.北京：电子工业出版社，2012：107- 113.）

Space object ground-based surveillance scheduling based on genetic-simulated annealing algorithm

YAN Qing-qing1，SHEN Huai-rong2，SHAO Qiong-ling2
（1.Department of Graduate Management，Equipment Academy，Beijing 101416，China；2.Department of Space Equipment，Equipment Academy，Beijing 101416，China）

Space object surveillance has a vital role in the smooth development of space mission.To solve the large-scale and complex scheduling problem of space object ground-based surveillance，a mathematical model with multiple constraints and optimal objectives is established.Through discussing a hybrid strategy of algorithms to local optimize a part of the global solution using the genetic algorithm to improve utilization of sensor resources，a hybrid algorithm with genetic algorithm and simulated annealing algorithm is constructed.A heuristic method is used to construct parts of solution for vague requirements，and a method named window trimming is used to solve time window conflicts in the hybrid algorithm.Simulation results show that the geneticsimulated annealing algorithm and window trimming method can receive a satisfactory solution in the acceptable term，which verifies that the model and algorithm are validity.

space surveillance；optimized scheduling；simulated annealing algorithm；genetic algorithm

V 556

10.3969／j.issn.1001-506X.2015.12.16

鄢青青（198-6- ），博士研究生，主要研究方向为航天装备总体理论与技术。

E-mail：yqwork2013＠163.com

沈怀荣（195-4- ），教授，博士，主要研究方向为航天装备总体理论与技术。

E-mail：shenhuair＠tom.com

邵琼玲（1971- ），副教授，主要研究方向为航天装备应用。

E-mail：zzy5678＠126.com

1001-506X（2015）12-2764-08

2014- 12- 24；

2015- 06- 12；网络优先出版日期：2015- 09- 21。