群体选择结果的稳定性分析及其度量方法

2015-06-05吴凡，陈阳，赵勇

系统工程与电子技术 2015年12期

关键词：稳定度测度度量

吴凡，陈阳，赵勇

（1.华中科技大学自动化学院系统工程研究所，湖北武汉430074；2.江苏省邮电规划设计院有限责任公司，江苏南京210000）

群体选择结果的稳定性分析及其度量方法

吴凡1，2，陈阳1，赵勇1

（1.华中科技大学自动化学院系统工程研究所，湖北武汉430074；2.江苏省邮电规划设计院有限责任公司，江苏南京210000）

群体选择的结果往往受个体主观因素的影响而具有一定的波动性，需要借助某些分析工具来考察其稳定或可靠程度。文中采用几何学方法，针对一类典型、常见的群体选择方法——加权计分规则（weighted scoring rules，WSRs），提出了一种基于评分向量夹角正弦的稳定性分析和度量方法，结合三候选方案情况阐述了该方法的合理性和相关概念的直观几何解释，给出了具体求解方法及其证明，并进一步针对候选方案数不同时可能引起的稳定度可比性问题扩展了相关问题、概念和方法。本文提出的群体选择结果的稳定性度量方法具有较好的直观性和可公度性，可作为多目标群决策问题中稳定性或敏感性分析的一个有力工具。

群体选择；向量夹角；稳定度；扰动评分向量

0 引言

稳定性分析的目的是获知某些关键参数发生改变的情况下决策结果的可靠程度，是多人多目标决策分析的一个重要环节或经典问题。在决策分析的研究领域，专家学者大多致力于探讨多目标决策的稳定性问题。例如，文献［1- 2］分别针对可加性多属性决策问题和贝叶斯环境下的多目标决策问题，提出了基于L2距离测度的稳定度概念，旨在利用属性或权重之间的最短距离（或差）对其稳定性进行度量；文献［3］将稳定性概念引入到决策过程中的概率误差估计环节，将L2距离测度扩展为任意范数，提出了基于线性规划模型求解的LP距离稳定度；文献［4］针对区间数多属性决策中基于“期望方差”的排序法，采用L2距离测度给出了两个方案之间排序位置颠倒时某一指标的权重最小变化量计算方法；文献［5］针对复杂系统的综合评估建模问题，进一步提出了权向量到无差异边界的最短距离和最长距离综合考虑的稳定度概念。由于群体选择比多目标决策要复杂得多，到目前为止关于其稳定性问题的研究并不多见。文献［6］以质量置信区间为依据，通过判断群体选择结果是否落在置信区间内来确定层次分析法中准则权重的稳定性；文献［7- 8］针对加权计分规则（weighted scoring rules，WSRs），借助基于距离的权重稳定度概念，研究了WSRs中Condorcet效率以及偏好断面逼近单峰偏好的问题；文献［9］针对基于OWA算子的群体选择方法，考虑在保持任意两个方案优劣关系不变的条件下，给出了在保持群意见稳定的条件下专家评价信息允许变化范围的计算方法；文献［10］研究了内生政策下委员会决策的稳定性问题，并结合单核概念给出了多数票规则下稳定策略存在的充要条件。从文献来看，现有的这些多目标决策和群体选择的稳定性研究大多建立在狭义或广义距离测度的基础上，而文献［11］从几何角度指出了这类稳定度概念的局限性，即数据的归一化或标准化使得不同维度下基于距离测度的稳定度的直观性和可比性不强。本文尝试探讨基于非距离测度的稳定性度量方法［12］。

投票几何学［13］是Saari提出的一种借助几何分析工具来解释和表达诸如投票一类社会选择问题的理论，并从几何解释和建模出发系统地研究了三候选方案下WSRs、Condorcet等群体选择方法的投票规则、策略、悖论和选择结果的概率估计等问题。考虑到大部分群体选择方法都可以归结为WSRs范畴，本文结合最优化理论［14］与投票几何学方法，主要针对WSRs提出和探讨了一类基于评分向量间夹角正弦的稳定性度量方法及相关算法。

1 问题描述

设群体选择问题由m（m≥2）个投票人和n（n≥2）个候选方案构成，并记Vm＝｛v1，v2，…，vm｝为投票人集合或群，Cn＝｛c1，c2，…，cn｝为候选方案集合，其中vi和cj分别表示第i个投票人和第j个候选方案。

本文讨论的群体选择规则WSRs是一类规则的总称，以权值向量的不同区分具体规则或选择函数。具体讲，权值向量W＝（w1，w2，…，wn）T定义了某个具体的加权计分规则（weight scoring rule，WSR），其中w1≥w2≥…≥wn≥0且w1＞wn。若投票人vi的选择中将方案cj排在第k位，那么权向量W中第k个分量wk就是vi对cj的评价值。WSRs要求群中个体或投票人对Cn中的所有候选方案均能给出完全序。

进一步地，所有投票人对方案cj的评价值之和sj称为方案cj的总评分，而称S＝（s1，s2，…，sn）T∈为群Vm的总评分向量，并记其在n维空间中对应的点为S，其中是一个n维向量的集合，表示在给定群Vm、候选方案集Cn和具体WSR选择规则的情况下S的取值范围。这里，可以具体表示为

式中，N表示自然数集；W是由WSR确定的权向量。

其中，aij表示将方案ci排在第j位的投票人数。

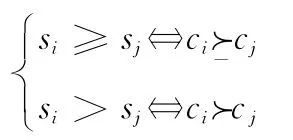
式中，≻和≻分别表示“优于”和“不劣于”关系。下面，以候

－选方案数n＝3的情况为例对做进一步说明和解释。记候选方案集合C3＝｛c1，c2，c3｝，权值向量W＝（w1，w2，w3）T≥0，那么在群Vm中存在6种可能的个体选择排序，如表1所示。其中，mi∈N（i＝1，2，…，6），且

表1 三候选方案情况下群Vm的一个投票断面

由表1可知，方案c1、c2和c3的总评分分别如下：

于是

显然A中各元素均为非负整数，每行每列元素之和都等于m。

定义1 给定WSR的权值向量W＝（w1，w2，…，wn）T和候选方案集Cn＝｛c1，c2，…，cn｝。对于n维向量F＝（f1，f2，…，fn）T，如果∃λ＞0且∃m∈N＋，其中N＋表示正整数集，使得λF∈Ω，则称F为该WSR的一个可行评价结果，简称可行结果。

定义1的含义是，一个可行结果F就是基于WSR的某个群体选择总评分向量的1／λ。因此，可行结果是对WSRs中评分向量的一种扩展，即两者的矢量方向是一致的。显然，WSRs下的总评分向量一定是可行结果，反之不一定成立。下面，给出可行结果的一个重要性质。

证毕

本文讨论的群体选择稳定性问题是指在保持群体选择结果（即候选方案间排序关系）不变的条件下群Vm的总评分向量的允许变化范围。范围越大，则说明结果越稳定。具体地，给定WSR的权值向量W、候选方案集Cn和群Vm的总评分向量S0∈Ω，设另一个群Vk的总评分向量为S′∈Ω，如果群Vm＋k的总评分向量S＝S0＋S′∈Ω所代表的候选方案排序和S0所代表的候选方案排序完全相同，那么S′的允许取值范围就体现了群Vm的选择结果、即总评分向量S0的稳定程度。为便于叙述，不妨称群Vk为扰动群，而称S′为扰动群Vk的扰动评分向量。

2 基于评分向量夹角的稳定性度量方法

2.1 基于角度的稳定性度量

先对群的总评分向量S的取值范围进行划分。

定义2 给定WSR的权值向量W、候选方案集Cn＝｛c1，c2，…，cn｝、群Vm及其总评分向量S＝（s1，s2，…，sn）T∈Ω，以及i，j∈｛1，2，…，n｝且i≠j，那么集合Ω可以划分为

或

其中

当群Vm的总评分向量S0∈Ω（i～j）时，如果扰动评分向量S′中关于ci和cj的评分值s′i≠s′j，则必然有S＝S0＋S′和S0所代表的候选方案排序不同——这是S0稳定性最差的一种极端情况。为了简化问题、并不失一般性，本文后续部分将只讨论S0∈Ω（i≻j）的情况。

通常，距离测度会受原始数据标准化或预处理的影响而导致相关度量不具有不变性和可公度性。而基于角度的测度可不受数据变换的影响，具有不变性、直观性和一定的可公度性［11］。定义3给出了一种基于角度的稳定度概念。

上述定义中，S′＝S－S0可视为扰动评分向量。由于稳定角和稳定度的定义与S′无关，因此定义3中采用变量α，而不用常量m＋k。这表明S是一个变量，不可以事先规定它所在的超平面或扰动群的规模k，这样做可以使上述定义更具一般性。另外，由于向量S0和S的各分量均不小于0，表明S0和S均在第一象限，因此可以规定θij∈［0°，90°］和σij∈［0，1］。图1是两候选方案情况下稳定角的一个示意图。

图1 两候选方案情况下稳定角示意图

图1中，二维空间的两个坐标轴分别表示方案c1和c2的评分值s1和s2，线段X0Y0和XY分别为总评分点S0和S所在超平面（二维空间中即为线段），M0和M分别表示线段X0Y0和XY的中点。根据定义2可知，⊂X0Y0（1≻－2）⊂X0M0（2≻－1）⊂Y0M0且（1≻2）⊂X0M0＼M0，线段XY的划分类似于X0Y0，只是线段上点的坐标不同而已。因为S0∈X0M0＼M0，S∈YM，所以根据定义3，S0关于（2－≻1）的稳定角θ12＝〈S0，M〉，其中M∈（1～2）。

定义3只是一个局部稳定度的概念。下面，进一步定义“全局稳定度”。

定义4 给定WSR的权值向量W、候选方案集Cn、群Vm及其总评分向量S0∈Ω（ρ1≻ρ2≻…≻ρn），其中ρl∈｛1，2，…，n｝（l＝1，2，…，n）表示群体选择结果中排在第l位的候选方案，且i≠j时ρi≠ρj，Ω（ρ1≻ρ2≻…≻ρn）表示满足cρ1≻cρ2≻…≻cρn的总评分向量集合，则称θ＝mini，j∈｛1，2，…，n｝andi＜jθρiρj为S0的全局稳定角，而称σ＝sinθ为S0的全局稳定度。

为了便于理解定义4，以S0∈Ω（1≻2≻…≻n）为例说明。此时，ρl＝l（l＝1，2，…，n），全局稳定度可以表示为σ＝mini，j∈｛1，2，…，n｝andi＜jsinθij。综合定义3和定义4可知，θ越大，则σ越大，即群体选择结果保持不变的前提下S0的可扰动范围越大，意味着群体选择结果越稳定。命题1给出了稳定度σij的计算方法。

命题1 设ci，cj∈Cn且ci≠cj，S0∈Ω（i≻j），则S0关于Ω（j≻i）的稳定度un）T为规划Prog1的解。

证明由定义3可知，S0∈Ω（i≻j）关于Ω（j≻－i）的稳定度中的S满足规划

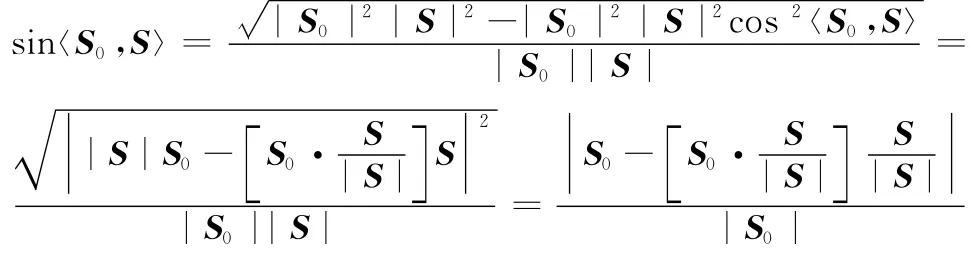
式中，S0·表示向量S0和的内积。，因此有

易证sin〈S0，S〉＝sin〈S0，φS〉＝sin〈S0／φ，S〉，式中，φ＞0和φ＞0。令U＝φT，于是，min｜S0－U｜＝min｜S0－φT｜＝UTminφ｜S0／φ－T｜⇔min｜S0／φ－T｜⇔min sin〈S0／φ，S〉⇔TTSmin sin〈S0，S〉，这表明Prog1和Prog1′的目标是等价的。S

由于向量S0和S的各分量均不小于0，或者说，它们均位于第一象限，因此｜（1－λ）S｜＜｜λS0＋（1－λ）S｜，于是sin〈S0，S1〉＜sin〈S0，S〉。由此可知sj＞si时sin〈S0，S〉不可能达到最小值，因此sin〈S0，S〉取最小值时必有si＝sj，对应于Prog1则有ui＝uj。

因此，Prog1和Prog1′的约束条件等价。

综合上述分析，Prog1和Prog1′的目标和约束条件均等价，即命题得证。证毕

不难发现，上述命题1及其分析中尚存在一些不足，即命题1的成立还需要保证Prog1的解U是WSR的一个可行结果，即U和中某个向量的方向必须相同。由Prog1可以判断出，U就是S0到（超）平面的一个垂足，下面证明该垂足是WSR的一个可行结果，并求出它的具体值。

命题2 给定WSR的权值向量W，规划Prog1的解U是WSR的一个可行结果。

证明显然，Prog1是一个凸规划。对于规划Prog1中的各约束条件分别引入广义拉格朗日乘子λ1，λ2以及γ1，γ2，…，γn，并设U＝（u1，u2，…，un）T是一个满足下述K－T条件的点［14］：

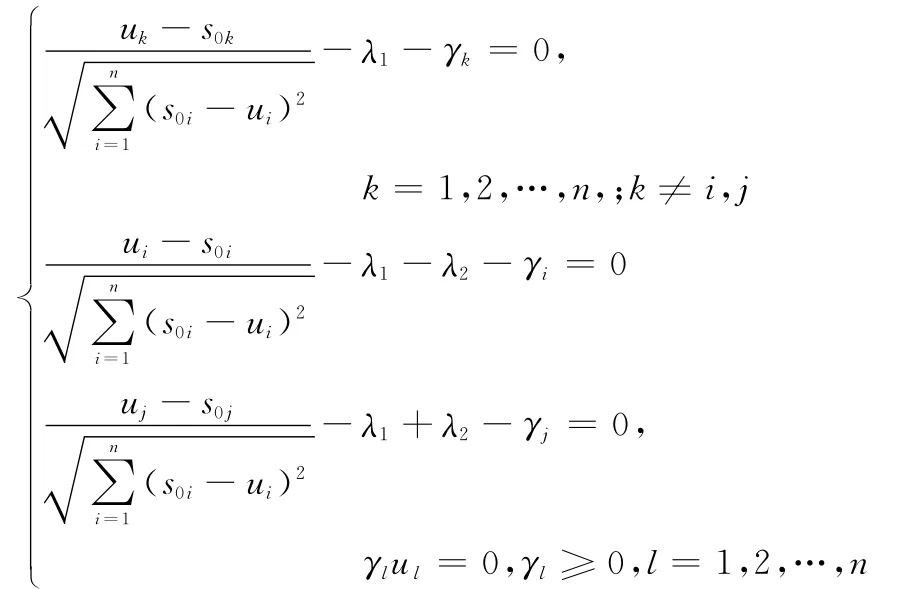
求解上述方程组可得到规划Prog1的解U，式中

证毕

由命题2的证明过程可以得到推论1。

推论1 规划Prog1的解U＝（u1，u2，…，un）T中，uk＝

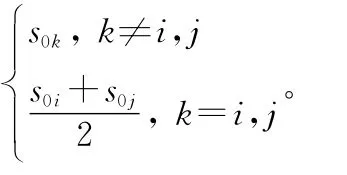
2.2 与基于距离测度的稳定性度量的比较

Saltelli A从几何角度指出了基于距离测度的稳定性度量的局限性，即数据的归一化或标准化使得不同维度下基于距离测度的稳定度的直观性和可比性不强。本节从群体选择这一特定类型的问题出发，对比分析两种稳定性度量的合理性及各自的适用范围。

（1）当k和W均为常量时，S0的稳定度可以采用基于角度或距离测度的度量。此时，S0离Ω（i～j）的距离越远，S0与对应的U之间形成的角度越大，意味着S0对应的群体选择结果越难以改变，即S0越稳定。值得一提的是，当k＝0时，S0的稳定度仍然可以采用两种度量方法中的任一种，然而这并非本文讨论的模型范畴，故不予详述。

（3）当W为常量，而k为变量时，基于距离测度的度量方法可能出现无法公度和比较的现象，此时基于角度的度量方法可以克服这一缺陷。这种情况下基于距离测度的度量方法的缺陷是群体选择问题所特有的。

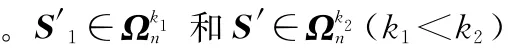
图2 基于距离的稳定性度量的缺陷

3 基于三候选方案的几何解释与分析

本节对n＝3情况下群体选择稳定性的概念做更直观、更一般的几何解释与说明。n＝3情况下的几何作图类似于n＝2的情况，即将3个候选方案c1、c2和c3的得分值s1、s2和s3分别定义为三维空间中的3个坐标。由式（1）可知，群的总评分向量必然位于某个超平面上，具体情况如图3所示。

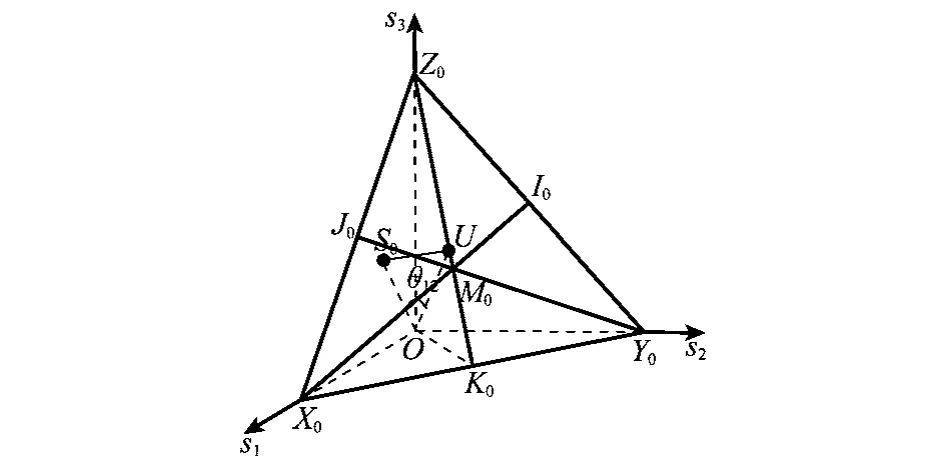
图3 三候选方案情况下S0的稳定角示意图

图3中，ΔX0Y0Z0表示群Vm的总评分点S0所在的超平面（在三维空间中即为平面）区域，其3个顶点的坐标分别为X0，0，0），Y0（0，Q，0）和Z0（0，0，Q），边界Y0Z0、X0Z0和X0Y0上的点表示3个方案c1、c2和c3的得分值分别为0的总评分点，而ΔX0Y0Z0的中心点M0则对应于方案c1、c2和c3的得分值相等的总评分点。另外，I0、J0和K0分别为边界Y0Z0、X0Z0和X0Y0上的中点，于是由定义2可知⊂ΔX0Y0Z0（1≻2）⊂ΔK0X0Z0（1～2）⊂K0Z0－和（1≻2）⊂ΔK0X0Z0＼K0Z0，其中ΔK0X0Z0＼K0Z0表示ΔK0X0Z0去掉边界K0Z0后的区域。具体地，位于ΔX0Y0Z0各区域内的总评分点S0与对应的方案优先关系如表2所示。

表2 各方案优先关系对应的S0所在区域

图3中，S0∈ΔK0X0Z0＼K0Z0，ΔX0Y0Z0⊥ΔOK0Z0，且S0U⊥K0Z0，U为S0在直线K0Z0上的垂足。因此由命题1和命题2知，稳定角θ12＝〈S0，U〉。显然，当S0处于ΔX0Y0Z0的中线I0X0，J0Y0或K0Z0上，即S0∈（1～2）∪（1～3）∪（2～3）时，S0的稳定度最小。例如S0∈（1～2），此时只要给出的任一个扰动评分向量S′∉（1～2），群Vm选择结果必然发生改变。

下面，命题3给出了三候选方案情况下群体选择结果的全局最大稳定度及对应的总评分向量的特征。

命题3 设A1∈X0J0为图3中ΔX0Y0Z0边X0Z0上的一个三等分点，S0为ΔX0J0M0内任意一点，且它们的全局稳定度分别为σA1和σS0，则有σA1≥σS0。

图4 三候选方案情况下具有最大稳定度的总评分向量A1

证明由于ΔX0Y0Z0是等边三角形，线段X0A1＝X0Z0，因此根据图中的几何关系可知，A1M0是∠X0M0J0的角平分线，且可证明A1到边I0X0和边J0Y0的距离相等，并小于A1到边K0Z0的距离。

另外，当S0∈ΔA1M0J0时，S0的全局稳定度σS0＝sin〈S0，U〉，其中U为S0在直线Y0J0上的垂足。连接并延长M0S0与X0Z0相交于S1，在四面体OM0J0S1中显然有∠J0OS1＞∠UOS0。而∠J0OA1＞∠J0OS1，因此∠J0OA1＞∠UOS0，即sin〈A1，J0〉＞sin〈S0，U〉，只有当S0与A1重合时sin〈A1，J0〉＝sin〈S0，U〉。综上分析，当S0∈ΔA1M0J0时，σA1≥σS0。

当S0∈ΔA1M0X0时，利用σ23同样可以证明σA1≥σS0。因此，在ΔX0J0M0中A1的稳定度最大，即σA1≥σS0。证毕

根据命题3的证明过程及对称性易知，ΔX0Y0Z0边上的其他三等分点Ai（i＝2，3…，6）对应的总评分向量的全局稳定度同A1相等，都是最大的。

4 相对稳定度

虽然全局稳定度σ体现了群体选择结果S0发生改变的难易程度，且具有一定的不变性和可公度性，但是在某些情况下，决策者直觉上可能仍然难以把握。例如，给定候选方案集Cn、群V30和Borda选择规则（即W＝（n－1，n－2，…，0）T），考虑两种情况：①n＝2，候选方案集合C2＝｛c1，c2｝，群的总评分向量S′0＝（20，10）T；②n＝3，C3＝｛c1，c2，c3｝，S″0＝（60，30，0）T。根据命题1和命题2，计算可得S′0和S″0的全局稳定度均为／10。由第4节的几何分析可知，10是n＝3情况下能达到的最大全局稳定度；而n＝2的情况却并非如此，借助图1可知其最大全局稳定度能够达到／2（当S0＝（30，0）T或（0，30）T时）。因此，／10并不能完全表明n＝2和n＝3两种情形下群体选择结果的全局稳定性的比较情况。由此例可见，相同的全局稳定度在不同方案数情况下群体选择结果发生改变的难易程度不完全相同，因此我们还需要考虑不同方案数情况下稳定度的可比性。

请注意：定义5中向量T可能不是WSR的可行结果或总评分向量，因此最大稳定度σn－max只是一个理论上具有参考价值的稳定度，或者说是一个理想的参考稳定度。但是，T的全局稳定度计算方法类似于S0∈，区别在于T不受属于的限制。显然，计算相对稳定度σr的关键在于σn－max的获取。下面的引理给出了σn－max对应的向量T的一个必要性质。

引理2 给定WSR的权值向量W、候选方案集Cn、群Vm及其总评分向量S0＝（s01，s02，…，s0n）T∈（1≻2≻…≻n）。若S0的全局稳定度σ＝σij，其中为S0关于i）的稳定度，U＝（u1，u2，…，un）T，那么ui＝uj且j－i＝1。

显然，这与S0的全局稳定度σ＝σij矛盾。因此j－i＝1。

证毕

如果将引理2中的S0∈（1≻2≻…≻n）改为定义5中的T，则相关结论仍然成立。根据引理2，可以推导出σn－max及其对应的向量。

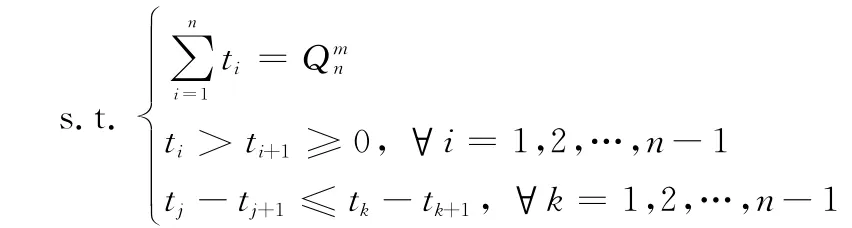
根据Tmax进一步计算可以得到最大稳定度的表达式为

证毕

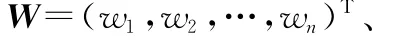
表3 Borda规则下最大稳定度及对应的总评分向量

5 案例分析

某软件开发公司主营财务分析类和产品质量检验类软件。为拓展公司的业务，由研发团队制定了4项未来的开发项目：

（1）c1某大型超市的供应链管理信息系统；

（2）c2某事业单位的协同办公管理系统；

（3）c3某电子商务网站的个性化推荐系统；

（4）c4某汽车制造企业的产品创新设计系统。

由于公司的人员和财力所限，当前只能从候选方案集C4＝｛c1，c2，c3，c4｝中挑选出一个进行实施。公司评估新项目开发的指标体系如表4所示。

表4 新项目开发评估指标

公司召开董事会会议进行投票表决，群体选择规则选用Borda规则。公司董事会由7名成员组成，即V7＝｛v1，v2，v3，v4，v5，v6，v7｝，其中｛v1，v2，v3，v4，v5｝是执行董事（常务董事），｛v6，v7｝是非执行董事（外聘专家）。各董事由于考虑问题侧重点的差异，给表4中评估指标赋予的主观权重有所不同。投票表决之前，董事长对C4＝｛c1，c2，c3，c4｝中的每个候选方案进行了介绍。各董事经过思考，对C4中的所有候选方案给出了一个完全序，如表5所示。

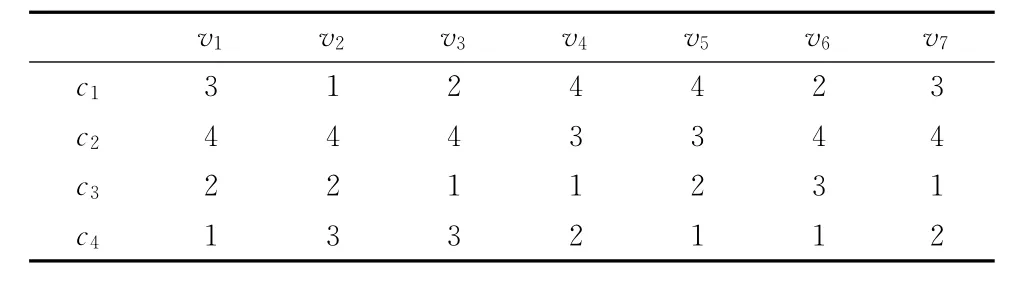
表5 董事会的投票断面

根据Borda规则对表5中的投票断面进行汇总，得到总评分向量S0＝（9，2，16，15）T。投票结果表明，c3≻c4≻c1≻c2，候选方案c3获胜。

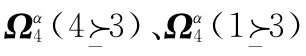
表6 董事会扩大会议的投票断面

采用Borda规则对表6中的投票断面进行汇总，得到总评分向量S′0＝（s3，s4）T＝（15，18）T。投票结果表明，c4≻c3，候选方案c4获胜，投票结果与董事会会议相比发生了改变。

S′0关于（3≻4）的稳定度σ′43≈0.090 5，对应的稳定

－角为arcsin0.149 8≈5.194 4°。表3中，σ2－max≈0.707 1，由此可以算得相对稳定度≈0.128 0。结果表明，σ34＜σ′43，但＞。因此考虑到选择的稳定性，方案c3和c4的优先顺序仍然难以区分，可以认为它们是无差异的，任选一项即可。

6 结论

考虑到基于距离测度的稳定度的缺陷，本文针对一类典型的群体选择方法——WSRs提出了一种基于评分向量间夹角正弦的稳定性度量方法，并探讨了具体求解方法及其扩展问题。本文给出的稳定角和稳定度的概念仅与具体的评分向量有关，而与采用的WSRs规则、投票人数和候选方案数均无关，因此具有较好的适用性、直观性和可公度性。为了克服不同候选方案数引起的稳定角或稳定度的不可比性，通过引入最大稳定度作为理论上的参考值，进一步提出了相对稳定角和相对稳定度的概念，以方便决策者对群体选择结果的稳定或可靠程度有更准确的把握。本文探讨的群体选择结果的稳定性度量方法可以用于社会选择领域与稳定性分析相关的诸多理论问题的研究。

［1］Barron H，Schmidt C P.Sensitivity analysis of additive multi-attribute value models［J］.Operations Research，1988，36（1）：122- 127.

［2］Insua D R，French S.A framework for sensitivity analysis in discrete multi-objective decision-making［J］.European Journal of Operational Research，1991，54（2）：176- 190.

［3］Ringuest J L.LP-metric sensitivity analysis for single and multiattribute decision analysis［J］.European Journal of Operational Research，1997，98（3）：563- 570.

［4］Wu C，Hu K.Sensitivity analysis to weight of priorities in multiple attribute decision making with intervals［J］.Systems Engineering and Electronics，2004，26（9）：1217- 1242.（吴超，胡昆.区间数多属性决策中权重灵敏度分析［J］.系统工程与电子技术，2004，26（9）：1217- 1242.）

［5］Ravalico J K，Maier H R，Dandy G C.Sensitivity analysis for decision-making using the MORE method—a pareto approach［J］.Reliability Engineering&System Safety，2009，94（7）：1229- 1237.

［6］Madu C N，Kuei C H.Stability analyses of group decision making［J］.Computers&Industrial Engineering，1995，28（4）：881- 892.

［7］Gehrlein W V.The sensitivity of weight selection on the condorcet efficiency of weighted scoring rules［J］.Social Choice and Welfare，1998，15（3）：351- 358.

［8］Gehrlein W V.The sensitivity of weight selection for scoring rules to profile proximity to single-peaked preferences［J］.Social Choice and Welfare，2006，26（1）：191- 208.

［9］Fan Z P，Li H Y，Jiang Y P.Sensitivity analysis of group decision making method based on OWA operators［J］.Journal of Northeastern University（Natural Science），2004，25（11）：1114- 1117.（樊治平，李洪燕，姜艳萍.基于OWA算子的群决策方法的灵敏度分析［J］.东北大学学报（自然科学版），2004，25（11）：1114- 1117.）

［10］Kenfack J，Pongou R，Tchantcho B.The stability of decision making in committees：the one-core［J］.Economics Letters，2014，122（3）：390- 395.

［11］Saltelli A，Annoni P.How to avoid a perfunctory sensitivity analysis［J］.Environmental Modelling&Software，2010，25（12）：1508- 1517.

［12］Zhao Y，Huang C Y，Chen Y.Weight sensitivity measurement，analysis，and application in multi-attribute evaluation［J］.International Journal of General Systems，2013，42（8）：860- 869.

［13］Donald G Sarri.Basic geometry of voting［M］.Berlin：Springer-Verlag，1995.

［14］Wu Q Z，Hou FJ.Operationsresearch and optimization methods［M］.2nd ed.Beijing：China Machine Press，2013.（吴祈宗，侯福均.运筹学与最优化方法［M］.2版.北京：机械工业出版社，2013.）

Analysis and measurement methods of the stability of group decision making

WU Fan1，2，CHEN Yang1，ZHAO Yong1
（1.Institute of Systems Engineering，School of Automation，Huazhong University of Science and Technology，Wuhan 430074，China；2.Jiangsu Posts&Telecommunications Planning and Designing Institute Limited Liability Company，Nanjing 210000，China）

The result of group selection is always unstable with the influence of some individual subjective factors.Thus，it is necessary to analyze the stability or reliability of the decision result by some tools.A geometric measurement method of the stability of weighted scoring rules（WSRs）which are representative group selection rules is proposed based on the inclined angle of two score vectors.Rationality and geometric interpretation of this method are elaborated in the situation that the number of candidates is three，then the computing method of the stability degree and its proof are proposed.Considering the comparability problem of stability degrees with different numbers of candidates，extended concepts and solutions of the stability degree are also discussed.The proposed stability measurement method is well visualized and commensurable.It can be an effective tool of sensitivity or stability analysis in multi-objective group decision making problems.

group selection；inclined angle of vectors；stability degree；disturbance vector of scores

C 934

10.3969／j.issn.1001-506X.2015.12.20

吴凡（1988- ），男，博士研究生，主要研究方向为群决策理论。

E-mail：dragonwufan＠126.com

陈阳（1977- ），男，讲师，博士，主要研究方向为决策理论、社会网络分析。

E-mail：chenyang＠mail.hust.edu.cn

赵勇（1967- ），男，教授，博士，主要研究方向为决策理论、大型工程项目管理、系统分析与集成。

E-mail：zhiwei98530＠sohu.com

1001-506X（2015）12-2791-08

2015- 01- 10；

2015- 04- 27；网络优先出版日期：2015- 08- 31。