基于高斯过程回归的平方根UPF算法

2015-06-05高社生

系统工程与电子技术 2015年12期

关键词：平方根协方差高斯

孟阳，高社生，王维

（西北工业大学自动化学院，陕西西安710072）

基于高斯过程回归的平方根UPF算法

孟阳，高社生，王维

（西北工业大学自动化学院，陕西西安710072）

针对系统动力学模型不准确可能导致滤波精度下降，以及系统状态协方差阵可能出现的负定性问题，提出一种新的高斯过程回归平方根分解无迹粒子滤波（Gaussian process regression square-root decomposition unscented particle filter，GPSR-UPF）算法。在该算法中，采用高斯过程回归求取UPF的重要性密度函数。当系统模型不准确时，通过高斯过程回归学习训练数据，进而获取系统的回归模型及系统噪声协方差，同时引入平方根变换抑制系统状态协方差阵的负定性。将提出的GPSR-UPF算法应用到捷联惯导／全球定位系统（strapdown inertial navigation system／global positioning system，SINS／GPS）组合导航系统中进行仿真验证。结果表明，所提出滤波算法的性能优于基本的无迹粒子滤波算法，能提高组合导航系统的解算精度。

高斯过程回归；平方根分解；无迹粒子滤波；组合导航系统

0 引言

非线性滤波问题广泛存在于导航制导、自动控制以及信息通信等领域。当前，处理非线性问题常用的滤波方法包括扩展卡尔曼滤波（extended Kalman filtering，EKF）［1］，无迹卡尔曼滤波（unscented Kalman filtering，UKF），无迹粒子滤波（unscented particle filtering，UPF）［2］等。EKF将非线性模型进行Taylor级数展开，忽略高阶项以解决非线性系统的滤波计算问题。UKF算法基于无迹变换（unscented transformation，UT），采用确定性采样以近似非线性函数的概率分布，相对于EKF算法无需计算Jacobian矩阵。UPF算法采用UKF以获取重要性密度函数，利用状态空间中的加权随机样本集来近似实际后验概率分布。上述滤波方法在处理拥有确定系统模型和先验噪声协方差的问题时，能够获得较好的滤波精度。然而在很多工程问题中，精确的系统模型往往难以获取，传统的滤波器在面对此类情况时滤波精度明显下降。针对这一问题，本文将高斯过程回归（Gaussian process regression，GPR）与UPF算法相结合来解决由于系统误差导致的滤波精度下降问题，以获取更好的滤波效果。

高斯过程回归基于贝叶斯理论和统计学习理论，是一种全新的机器学习方法，适用于处理高维数、小样本和非线性问题，其泛化能力强且与神经网络和支持向量机相比具有更易实现、超参数自适应获取以及输出具有概率意义等优点［3］。近年来高斯过程回归被尝试应用于各个领域，并取得了一定的研究成果。文献［4］采用十进制遗传算法代替共轭梯度法搜寻高斯过程最优超参数，提高了高斯过程回归的泛化能力。文献［5］将高斯过程回归引入计量学领域，用于挖掘近红外光谱与被测物组分之间的复杂关系，从而获取了精度高、释放能力强的分析模型。文献［6］将GPR应用于无线电强度估计的定位问题中，取得了较好的定位效果。文献［4- 6］尝试了GPR在不同领域的应用，验证了其在工程领域的有效性。文献［7］将GPR与容积卡尔曼滤波相结合，采用GPR学习建立模型并通过容积卡尔曼滤波处理非线性问题，探讨了将GPR与非线性滤波算法相结合的新思路。然而，如何改善GPR与非线性滤波的融合效果并进一步提高滤波精度，是本文研究的重点。

本文提出一种适用于非线性系统的高斯过程回归平方根分解无迹粒子滤波（Gaussian process regression squareroot decomposition unscented particle filter，GPSR-UPF）算法。该算法将高斯过程回归融入UPF算法中，通过高斯过程回归求取UPF的重要性密度函数，当系统模型不精确时，GPR通过高斯过程实时学习训练数据，获取系统的回归模型及系统噪声协方差，提高模型精度；同时，采用平方根变换，利用协方差平方根代替协方差参加递推运算来保证系统状态协方差阵的正定性。将提出的GPSR-UPF算法应用到SINS／GPS组合导航系统中进行仿真验证。结果表明，该算法适用于非线性动态系统，能够降低由于系统模型变化所导致的滤波误差，提高导航解算精度。

1 高斯过程回归平方根UPF算法设计

考虑如下非线性系统：

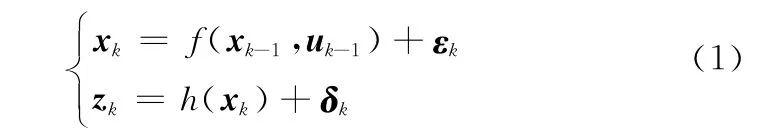
式中，xk，zk∈Rn分别为k时刻系统的状态向量和量测向量；uk为控制输入向量；εk∈Rn是系统噪声，其方差为Qk；δk∈Rn是量测噪声，其方差为Rk；f（·）和h（·）为非线性函数。

1.1 高斯过程回归

高斯过程回归是通过寻找训练数据之间的关系来对系统进行辨识的非参数黑箱模型［8］。其性质由均值函数m（x）和协方差函数k（x，x′）确定［3］，即

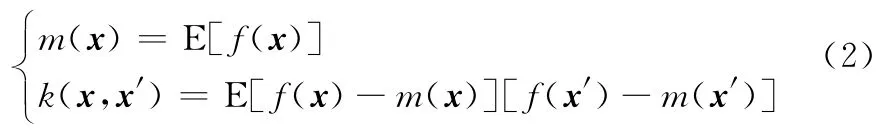
式中，函数f（x）的高斯过程（Gaussian process，GP）数学表达式为f（x）～GP（m（x），k（x，x′）），x，x′∈Rd是任意的随机变量。

对于回归问题，给出如下模型：

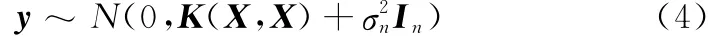
同时，有观测值y和预测值f*的联合先验分布为

式中，K（X，X）＝Kn＝（kij）为n×n阶对称正定协方差矩阵。矩阵元素kij＝k（xi，xj）用来度量xi和xj的相关性，x*为测试点，K＝K（K，x*）＝K（x*，X）T为测试点与训练集的输入X之间的协方差阵，k（x*，x*）为测试点x*自身的协方差，In是n维单位矩阵。

预测值f*的后验分布为

式中，均值和方差［9］分别为

通常采用平方指数协方差来求解协方差函数中的未知参数，有

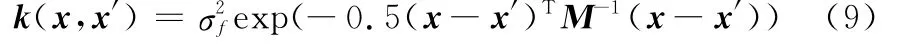
采用极大似然法求取超参数θ。建立似然函数

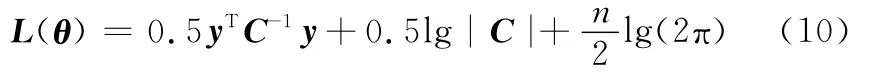
并对超参数θ求偏导，采用共轭梯度法对偏导数进行最小化以求取最优解［3］得

式中，C＝Kn＋In，α＝C－1y。获得最优超参数后，联合式（7）和式（8）即可求得测试点xi所对应的期望和方差。

1.2 平方根变换

在对粒子进行预测和更新时，要求状态协方差阵为非负定矩阵。然而在计算过程中，由于误差等因素可能使得滤波协方差负定或者不对称，从而导致滤波器发散，本文采用平方根变换来解决该问题。考虑L维随机变量x经过非线性变换后得到z＝h（x），假设x的均值和方差分别为x－和Px，且有x的Sigma采样点（xi）和权值ωi。将采样点进行非线性变换得到

计算得到均值和协方差，有

新算法在滤波过程中采用Sz替代Pz进行运算以抑制协方差阵的负定性。

1.3 高斯学习过程的状态和观测模型

高斯过程回归学习获取系统的状态方程、观测方程以及噪声协方差阵Q和R，其状态方程和观测方程的训练数据集为

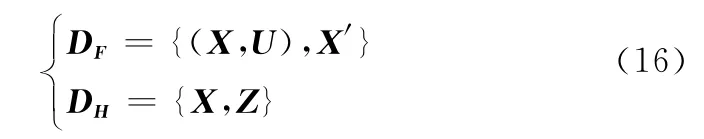
式中，X为状态阵；X′＝［Δx1，Δx2，…，Δxk］为状态转换矩阵，Δxk＝xk＋1－xk；Z是观测阵。高斯过程将状态方程f和观测方程h表示为GPF和GPH，则

式中，εk～N（0，GP［（xk－1，uk－1），DF］）；δk～N（0，GP（xk，DH））。

取式（16）与系统近似模型获取值之差为数据集，即通过高斯过程回归学习真实系统模型与近似系统模型的差［9］，有

联合系统近似模型与式（18）学习获取的系统模型，其状态方程和观测方程为

式中，εk～N（0，GP［（xk－1，uk－1），Df］）；δk～N（0，GP（xk，Dh））；为近似的系统状态方程；^h为近似的观测方程。由数据集式（18）学习获得的状态方程和观测方程分别表示为GP和GP。

1.4 提出的GPSR-UPF算法

本文所提出的GPSR-UPF算法将高斯过程回归融入UPF算法中，采用高斯过程回归方法提高系统模型精度以求取UPF的重要性密度函数；同时引入平方根分解，使用误差协方差阵的平方根代替协方差阵参与滤波以抑制系统状态协方差阵的负定性。具体算法如下：

（1）初始化并从先验分布中抽取粒子

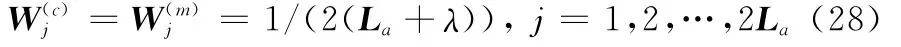
式中，La表示向量的维数；λ表示尺度因子；chol表示cholesky分解；α和β为控制采样点分散程度的参数。分别建立状态方程与观测方程的训练数据：Df，Dh。

（

2）计算Sigma点

通过高斯过程进行实时学习，时间更新：

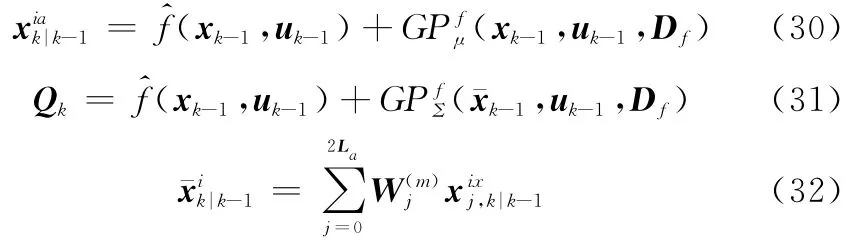
采用平方根变换，利用协方差平方根代替协方差参加递推运算以抑制系统状态协方差阵的负定性。

通过GPR学习获取观测值：

量测更新：

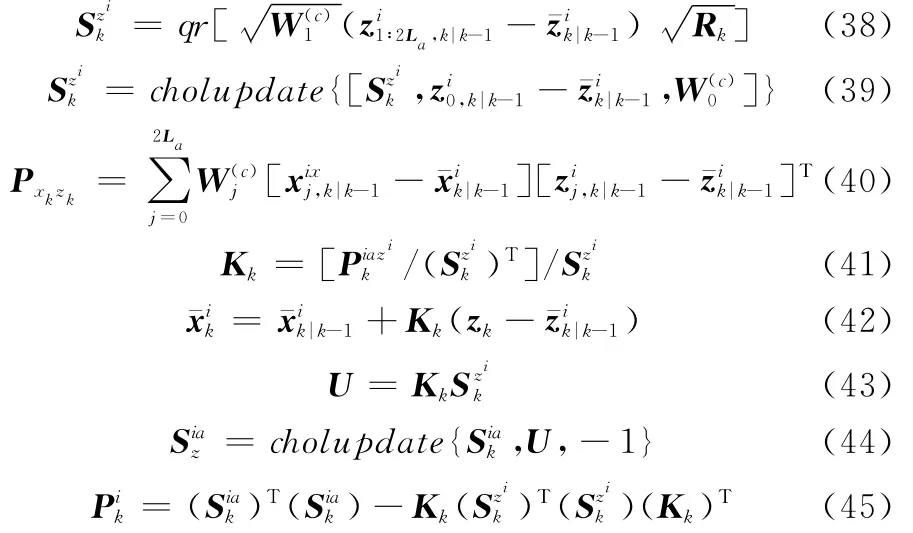
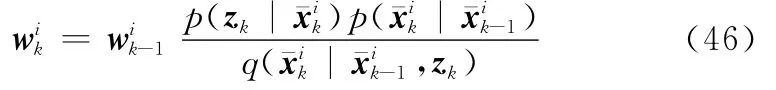
归一化权值得

（3）重采样

计算Neff，判断Neff是否小于阈值NT。如小于阈值，则进行重采样。Neff越小表示退化越严重。

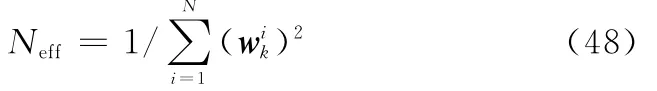
（4）状态量的估计值

2 SINS／GPS组合导航系统模型

捷联惯导（strapdown inertial navigation system，SINS）［10］与全球定位系统（global positioning system，GPS）两种导航方法具备互补特性，将SINS与GPS相融合进行组合导航，可以获取较高的导航精度。

2.1 组合导航系统的状态方程

SINS的姿态误差方程为

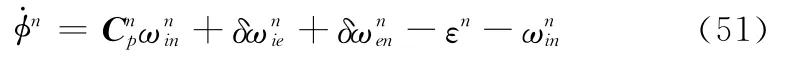
速度误差方程为

位置误差方程为

陀螺漂移误差模型表示为

式中，εb为随机常数；εr为一阶马尔科夫随机过程噪声；ωg为陀螺随机白噪声漂移。

加速度计误差模型为

式中，Tα为相关时间；ωα为加速度计随机白噪声漂移。

在东北天坐标系中，选取组合系统的状态量为

噪声随机误差矢量W为

2.2 组合导航系统的量测方程

采集SINS和GPS所输出的位置和速度信息，SINS的位置信息为

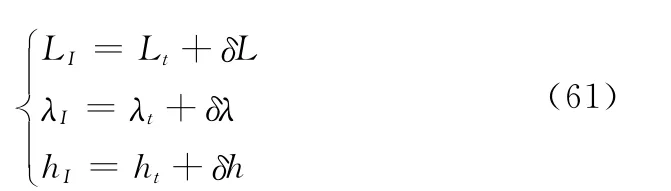
速度信息为

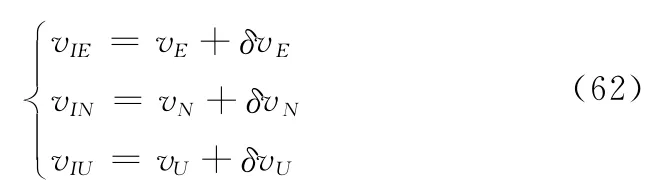
GPS输出的位置信息为

GPS输出的速度信息为

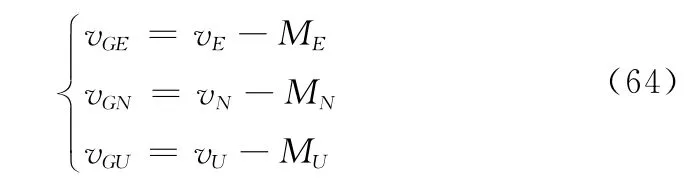
式中，vE，vN，vU是载体沿地理坐标系3个轴方向的速度真值；Lt，λt，ht是位置真值；ME，MNMU是GPS的测速误差；NE，NN，NU是GPS东，北，天三向的位置误差。

取SINS与GPS的量测量之差为观测信息，定义位置量测方程［11］为

即

其中，Vp（t）＝［NE，NN，NU］是系统位置信息量测噪声。

定义速度量测方程为

即

式中，Vv（t）＝［ME，MN，MU］是系统速度信息量测噪声。由此得到SINS／GPS位置和速度的联合测量方程为

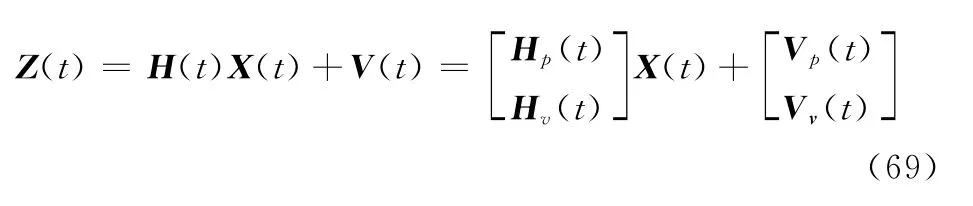
3 仿真分析

仿真实验重点验证了本文提出的GPSR-UPF算法和基本UPF算法在系统模型发生误差时的性能对比。为了验证本文所提出算法的优越性，分别将基本UPF算法以及改进后的GPSR-UPF算法应用于SINS／GPS组合导航中进行仿真对比。设飞行器初始位置为东经109°，北纬34°，高度1 000 m。陀螺常值漂移为0.01°／h，陀螺一阶马尔可夫过程漂移0.01°／，加速度计常值偏置10－4g，随机偏置为10－5g／，GPS测量噪声标准差为10 m的白噪声，SINS初始速度误差为0.5 m／s，初始位置误差为10 m，仿真时间1 000 s。飞行器飞行过程中进行各种机动动作，航迹包括滑跑起飞、爬升、匀速平飞、加速、盘旋等状态。其中，0～200 s飞行器做滑跑、起飞、爬升等动作，500～600 s时，飞行器做加速、盘旋等动作。具体仿真结果如图1～图6所示。

图1 基于UPF的位置误差估计

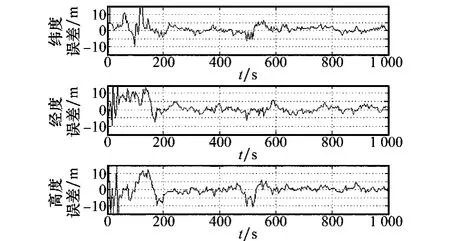
图2 基于GPSR-UPF的位置误差估计

图1和图2分别是基本UPF算法和本文提出的GPSR-UPF算法在组合导航系统中得到的位置误差曲线。可以看出，在匀速飞行时段，采用UPF算法得到的东向、北向以及天向的位置误差稳定在（－7.5 m，＋7.9 m）；而采用GPSR-UPF算法得到的东向、北向以及天向的位置误差稳定在（－4.9 m，＋4.9 m）。飞行器在0～200 s以及500～600 s两个时间段做变速机动运动，由仿真图可以看出，0～200 s时间段，GPSR-UPF算法相对于UPF算法，其位置误差估计受系统变化的影响要小于UPF算法；而在500～600 s时间段，GPSR的位置误差估计稳定在±10 m以内，而UPF算法的位置误差明显高于前者。

图3 基于UPF的速度误差估计

图4 基于GPSR-UPF的速度误差估计

图3和图4分别是UPF算法和本文提出的GPSRUPF算法在组合导航系统中得到的速度误差曲线。在匀速飞行时段，通过UPF算法计算得到的速度误差范围稳定在（－1.8 m／s，＋1.5 m／s）；而由GPSR-UPF算法计算得到的速度误差范围稳定在（－1.0 m／s，＋1.2 m／s）。飞行器在0～200 s以及500～600 s两个时间段做机动运动，0～200 s时间段，GPSR-UPF算法相对于UPF算法在速度误差估计上差别不大；在500～600 s时间段，GPSR的速度误差估计稳定在（－1.5 m／s，＋2.0 m／s）以内，而UPF算法的速度误差最高达到了3.3 m／s。

图5和图6分别是UPF算法和本文提出的GPSR-UPF算法在组合导航系统中得到的姿态误差曲线。在匀速飞行时段，通过UPF算法计算得到的姿态误差范围稳定在（－1.4′，＋1.6′）内；采用GPSR-UPF算法计算得到的姿态误差范围稳定在（－0.9′，＋1.0′）以内。飞行器在0～200 s以及500～600 s两个时间段做机动运动，在0～200 s时间段GPSR-UPF算法的位置误差明显小于UPF算法；在500～600 s时间段，GPSR的速度误差估计稳定在（－1.9′，＋1.6′）以内，而UPF算法的速度误差接近±3′，具体结果如表1所示。

图6 基于GPSR-UPF的姿态误差估计

表1 GPSR-UPF与基本UPF在组合导航中的仿真结果对比

通过表1的结果对比可以看出，飞行器在做匀速飞行时，GPSR-UPF算法的解算精度要高于UPF算法。而当飞行器做滑跑、爬升、加速、盘旋等机动动作时，随着飞行器轨迹的变化系统模型产生误差，此时GPSR-UPF能够降低系统模型误差对滤波性能的影响，保持较好的导航精度。新算法对于位置和速度的解算误差相比基本UPF算法能够降低约33%左右，其对于姿态的跟踪误差能够降低约40%。由此说明，改进的GPSR-UPF算法相对于基本UPF算法能够有效降低系统模型误差对滤波结果的干扰，获得更高的解算精度。

4 结论

本文提出的GPSR-UPF算法，首先将高斯过程回归融入无迹粒子滤波算法以求取UPF的重要性密度函数，降低了由于系统模型误差所导致的滤波误差。同时，在算法中引入平方根变换，利用协方差平方根代替协方差参与递推运算来解决系统状态协方差阵可能出现的负定性问题。最后，将该算法应用于SINS／GPS组合导航系统中进行仿真验证。结果表明，通过对目标系统模型的辨识学习，设计的GPSR-UPF算法能够降低系统误差对滤波精度的影响，在系统模型变化时保持滤波效率，其性能优于基本UPF算法，提高了组合导航系统的解算精度。

［1］Giannitrapani A，Ceccarelli N，Scortecci F，et al.Comparison of EKF and UKF for spacecraft localization via angle measurements［J］.IEEE Trans.on Aerospace and Electronic Systems，2011，47（1）：75- 84.

［2］Gerasimos G R.Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles［J］.Robotics and Autonomous Systems，2012，60（7）：978- 995.

［3］He Z K，Liu G B，Zhao X J，et al.Overview of Gaussian process regression［J］.Control and Decision，2013，28（8）：1121- 1129.（何志昆，刘光斌，赵曦晶，等.高斯过程回归方法综述［J］.控制与决策，2013，28（8）：1121- 1129.）

［4］Liu K Y，Fang Y，Liu B G，et al.Intelligent deformation prediction model of tunnel surrounding rock based on genetic-Gaussian process regression coupling algorithm［J］.Journal of the China Railway Society，2011，33（12）：101- 106.（刘开云，方昱，刘保国，等.隧道围岩变形预测的进化高斯过程回归模型［J］.铁道学报，2011，33（12）：101- 106.）

［5］Feng A M，Fang L M，Lin M.Gaussian process regression and its application in near-infrared spectroscopy analysis［J］.Spectroscopy and Spectral Analysis，2011，31（6）：1514- 1517.（冯爱明，方利民，林敏.近红外光谱分析中的高斯过程回归方法［J］.光谱学与光谱分析，2011，31（6）：1514- 1517.）

［6］Ferris B，Haehnel D，Fox D.Gaussian processes for signal strength-based location estimation［C］∥Proc.of the International Conference on Robotics，Science and Systems，2006：303- 310.

［7］Wei X Q，Song S M.Model-free cubature Kalman filter and its application［J］.Control and Decision，2013，28（5）：769- 773.（魏喜庆，宋申民.无模型容积卡尔曼滤波及其应用［J］.控制与决策，2013，28（5）：769- 773.）

［8］Taeryon C.Alternative posterior consistency results in nonparametric binaryregression using Gaussian process priors［J］.Journal of Statistical Planning and Inference，2007，137（9）：2975-2983.

［9］Jonathan K，Daniel J K，Dieter F，et al.GP-UKF：unseented Kalman filters with Gaussian process predietion and observation models［C］∥Proc.of the International Conference on Intelligent Robots and Systems，2007：1901- 1907.

［10］Gao S S，Wei W H，Zhong Y M，et al.Rapid alignment method based on local observability analysis for strapdown inertial navigation system［J］.Acta Astronautica，2014，94（2）：790- 798.

［11］Zhang K，Liu H P，Li H N，et al.SINS／GPS／CNS integrated navigation federal filtering algorithm［J］.Journal of Chinese Inertial Technology，2013，21（2）：226- 230.（张科，刘海鹏，李恒年，等.SINS／GPS／CNS组合导航联邦滤波算法［J］.中国惯性技术学报，2013，21（2）：226- 230.）

Square-root unscented particle filter based on Gaussian process regression

MENG Yang，GAO She-sheng，WANG Wei
（School of Automation，Northwestern Polytechnical University，Xi’an 710072，China）

In view of the uncertainty of the system dynamic model may reduce the filtering effect and the system state covariance matrix is negative definiteness，a new unscented particle filter（UPF）based on Gaussian process regression and square-root decomposition（GPSR）is proposed.The importance density function of UPF is gotten by Gaussian process regression.When the system model and observation model are inaccurate，Gaussian process regression is used to learn the training data，the regression models and noise covariance of the dynamic system are gotten；square-root decomposition is used to restrain the negative definiteness of the system state covariance matrix.The proposed algorithm is applied to the integrated navigation system of strapdown inertial navigation system／global positioning system（SINS／GPS）.The simulation results show that the proposed algorithm is better than UPF，and also effectively improves the positioning precision of the navigation system.

Gaussian process regression；square-root decomposition；unscented particle filter（UPF）；integrated navigation

V 249.32

10.3969／j.issn.1001-506X.2015.12.23

孟阳（198-5- ），男，博士研究生，主要研究方向为导航、制导与控制。

E-mail：27104683＠qq.com

高社生（1956- ），男，教授，博士研究生导师，博士，主要研究方向为导航、制导与控制。

E-mail：gshshnpu＠163.com

王维（1984-- ），男，博士研究生，主要研究方向为导航、制导与控制。

E-mail：413773558＠qq.com

1001-506X（2015）12-2817-06

2015- 01- 18；

2015- 04- 12；网络优先出版日期：2015- 08- 31。