系统可靠性方法研究现状与展望

贾利民，林 帅1，

（1.北京交通大学交通运输学院，北京100044；

2.北京交通大学轨道交通控制与安全国家重点实验室，北京100044）

系统可靠性方法研究现状与展望

贾利民2，林 帅1，2

（1.北京交通大学交通运输学院，北京100044；

2.北京交通大学轨道交通控制与安全国家重点实验室，北京100044）

如何依据部件的可靠性属性和系统的结构特性定量分析系统可靠性，是可靠性工程研究中亟待解决的重要问题之一。本文总结现有的系统可靠性分析方法，将其划分为4大类，即解析法、蒙特卡罗法、综合法和网络法，并对上述4种方法的优缺点及适用的系统进行了分析，最后指出将表征组成系统的各组份相互关系的拓扑结构和表征系统组份的节点可靠性属性相结合，构建新的可靠性测度指标评价系统可靠性是未来系统可靠性分析方法的研究趋势。

系统可靠性；复杂网络；故障树；状态空间

0 引 言

不同研究领域关于系统的定义略有不同。一般系统论的创始人Bertalanffy［1-2］认为“系统是相互联系相互作用的诸元素的综合体”。Langefors［3］给出系统的定义为“A system is a set of entities with variations”。Miller［4］则认为系统是一系列相关单元／元素的有机集合。钱学森［5］则定义系统是由相互作用、相互依赖的若干组成部分结合而成的，具有特定功能的有机整体，而且这个有机整体又是它所从属的更大系统的组成部分。虽然关于系统的定义有多种表述方式，但总体来说系统都具备以下3个基本特征：多元性、相关性、整体性。其中多元性表征了系统是多样性、差异性的统一；相关性表明系统中的元素／部件是相互依存、相互作用、相互制约的；整体性说明系统是由元素／部件所构成的复合统一整体。

现实世界中系统是普遍存在的，例如交通运输系统、生物系统、电力系统、计算机系统、教育系统等。依据系统中组份的数量以及组份间作用关系强弱，一般可将系统划分为简单系统和复杂系统。简单系统中的元素数目较少，元素之间的耦合关系微弱，典型的简单系统如串联系统、并列系统、混联系统等；而复杂系统中部件数量较多且部件间存在错综复杂的耦合作用关系，如电网系统、复杂机电一体化系统、Internet网系统等。从直观的视角来看，复杂系统又可划分为复杂网络系统和可用网络描述的复杂系统，其中复杂网络系统是指其外部呈现出典型网络的形状，例如电网系统、交通运输网、Internet网等；可用网络描述的复杂系统则是指其系统外部无显著的网络特性，但其内部结构却具有明显网络特性，例如，机电一体化复杂系统等。

系统可靠性分析一直是可靠性工程研究中的关键点与难点。系统可靠性一般是指在规定的时间内和规定的工况下，系统完成规定功能的能力／概率。由于科学技术的进步，系统的组成越来越复杂，随之产生的系统可靠性问题也日益突出。系统越复杂，意味着其承载的信息量越大，重要性越高、功能越强、适用范围也就越广，一旦失效所造成的损失也是巨大的，甚至是灾难性的。如何快速、有效、准确地对系统的可靠性进行评估与分析，正确估计系统的实际性能，减轻系统风险是具有极其重要的现实意义。

本文简要地回顾了系统可靠性分析方法的研究现状。首先介绍了近十年来利用FTA、状态空间法、GO法、Petri网、FMEA等解析方法对系统可靠性分析的研究现状，同时对近几年利用蒙特卡罗仿真法以及综合法研究系统可靠性的现状进行介绍；重点介绍了基于网络方法的系统可靠性研究状况；然后对比现有的多种系统可靠性分析方法的优缺点；最后指出当前复杂系统可靠性研究存在的问题以及未来的发展趋势。

1 系统可靠性分析方法

系统可靠性研究早期，以简单系统为主，系统中部件数量较少，且部件与部件间相互独立。针对这类型的系统，可靠性分析方法主要有故障树分析（fault tree analysis，FTA）、故障模式和后果分析（failure mode and effect analysis，FMEA）法等。随着现代工业技术的发展，系统的复杂程度提高，新的方法逐渐被提出并应用于分析系统可靠性，包括Markov法、GO法、Bayes法及其改进算法等。进入20世纪末，复杂网络理论的兴起，使得从网络的角度研究系统可靠性成为发展趋势。通过总结上述方法，将系统可靠性分析方法归为4大类，即解析法、蒙特卡罗法、综合法和网络法。

1.1 解析法

解析法通常是以部件的可靠性属性为基础，列举系统可能的故障状态，分析系统故障状态下各部件的行为特征，进而计算系统可靠性指标分析系统可靠性。解析法因其原理简单、计算速度快等优势，广泛应用于小规模系统或简单系统的可靠性评估。但解析法应用在复杂系统中存在以下缺陷：当解析法需要分析的系统空间状态数随部件个数呈指数规律增长时，计算过程过于繁杂；潜在假设认为部件与部件之间相互独立，与复杂系统部件耦合关系复杂相矛盾。

1.1.1 基于FTA的系统可靠性分析方法

FTA［6］是可靠性分析中最常用的方法之一。它以故障模式为基础，自顶向下分析系统的可靠性，即首先确定系统层的故障模式，依次查找引起上一层故障的全部可能故障，直到找出造成系统故障的全部基本底事件为止。

文献［7］证明了任何单调关联系统的可靠性都能用其最小割集组合的可靠性来表示，因此，对于部件较少，关联关系简单的系统，其系统可靠性分析可转化为求解最小割集问题。而对于部件数量较多，部件间耦合关系复杂的系统，直接应用FTA存在以下问题：最小割集如何求解、如何构建结构函数、系统中部件之间的关系如何描述等。针对复杂系统最小割集的计算，文献［8］提出将邻接矩阵的概念引入FTA中，构建最小割集矩阵／规则矩阵，通过矩阵变换求解最小割集。在构造结构函数时，文献［9- 10］引入Copula函数刻画最小割集内部件间的失效相关性，进而建立系统可靠性预计模型。FTA建立的故障树往往是静态的，但实际构成系统的部件的故障具有动态性，因此动态故障树（dynamic fault tree analysis，DFTA）［11］应运而生。DFTA引入了故障树结构和状态转移的动态特性［12-13］，定义标准动态特性的新逻辑门类型，建立动态故障树，进行局部相关部件的系统可靠性研究，从而完善系统可靠性模型的描述能力，实现更为准确的逻辑处理过程。

1.1.2 基于Petri网的系统可靠性分析方法

基于Petri网的可靠性建模是通过对系统进行详尽的了解和分析，建立Petri网模型；而后采用仿真方法对Petri网模型进行定量分析，得到系统的各个终态以及各条点火路径出现的概率。Petri网目前已在复杂系统可靠性建模与分析、故障诊断等可靠性工程领域中得到有效的应用。

文献［14］改进Petri网模型，提出一种新的衰老tokens，以此提高tokens的记忆能力。文献［15］提出基于动态可靠性框图的系统可靠性模型，并将其转换为有色Petri网进而研究系统可靠性。文献［16］建立基于Petri网与马尔科夫过程的系统可靠性研究模型。文献［17］提出一种基于Petri网-模糊λ－τ的系统可靠性分析方法，该方法用Petri网定性建模，用模糊λ－τ定量描述基本事件的模糊三角隶属函数关系。文献［18］针对离散时间动态系统利用Petri网分析系统可靠性时，为了避免系统状态空间爆炸的情况出现，将Petri网的可达性等价转换为线性逻辑库。文献［19］基于Petri网的动态行为特征，将其映射到马尔科夫状态空间，构建不计时Petri网模型的可达图，进而分析系统的可靠性。

1.1.3 基于状态空间法的系统可靠性分析方法

状态空间法通常以可靠性工程中马尔科夫模型［20］为基础，分析系统状态变化过程，构建状态转移方程，统计分析系统可靠性指标。状态空间法适用于状态空间数目较少的系统，可依次枚举系统的所有状态，分析系统可靠性。

但是，现实中系统状态空间数目往往巨大，因此文献［21］提出在短时期内，对多状态系统利用马尔科夫模型进行可靠性分析。文献［22］给出的GENERATE算法能够产生系统实际运行时最可能出现的状态，从而减少系统状态空间的数量。文献［23］以系统状态概率不增的次序生成系统最大概率值有效状态，修正了GENERATE算法，降低系统状态空间数目。马尔科夫模型中假设部件的状态仅有正常和故障两种，但事实上部件的状态却有多种，例如正常、故障、维修等，并且部件的故障率、修复率等参数获取也有一定的难度。文献［24］提出差分重要性测度，估计多状态部件的参数值。文献［25］提出将模糊理论与马尔科夫模型相结合，计算模型中部件的故障率和修复率。文献［26］结合泰勒展开式，建立马尔科夫链的生成矩阵群的逆函数，利用逆函数计算系统可靠性的概率密度函数。在以马尔科夫模型为基础的系统可靠性研究中多以状态转移函数服从指数分布为假设前提，而工程实际中预防性检修间隔时间等均为非指数分布。为了克服上述问题，半马尔科夫模型被提出。半马尔科夫模型［27］是一个随时间而变化的一维连续参数的随机过程，且不需要对状态转移函数作指数分布假设。半马尔科夫模型不具有马尔科夫性，其将来状态取决于现在状态和在该状态停留的时间。

1.1.4 基于GO法的系统可靠性分析方法

GO法［28］是以功能流为导向，将系统的原理图或工程图按一定的规则转化成为GO图，进而定性或定量的分析系统可靠性的方法。与FTA不同，GO法主要反映的是系统顺序操作过程及部件之间的功能作用关系，而FTA则反映了造成系统故障的各种原因及其逻辑关系。

目前，GO法及其改进算法已广泛应用于各类型系统的可靠性分析中，文献［29］用GO法代替计算复杂组合的可靠性联合概率，降低了计算机编程实现的难度。文献［30］提出将最短路径集与GO法相结合，使得GO法利用计算机编程实现的难度进一步降低。文献［31］将GO法应用于供应链系统的可靠性分析中，把系统可靠性计算问题转换为求对应等效节点的可靠性问题。文献［32］利用GO法对存在共因失效的多阶段任务系统进行可靠性建模分析。近年来，GO法广泛的应用在供电系统［33］、汽车制动系统［34］、核能系统［35］等机电一体化的复杂系统的可靠性分析中，并取得了一定的成果。在GO法的基础上，一种适用于时间序列问题和多状态系统阶段任务问题的GO-FLOW方法［36］被提出用于分析系统的可靠性。

1.1.5 基于FMEA法的系统可靠性分析方法

FMEA法是一种定性的归纳分析系统可靠性的方法［37］。依据系统的故障维修数据，依次辨识系统中每一个部件所有可能的故障模式以及对其他部件、子系统和系统的影响。FMEA法依据研究目标不同，可靠性研究深度、结果的表达形式等也各有不同。目前，FMEA多与FTA相结合，通过对故障模式的分析，为FTA的构建提供辅助支持。

文献［38］认为FMEA并未将相互依存在各种失效模式之间的不确定信息纳入考虑范围，其结果的有效性也是值得怀疑的，因此提出模糊逻辑FMEA法克服信息共享存在的困难。为了使FMEA能够对系统的可靠性进行定量分析，风险优先数［39］、加权风险优先数［40］、模糊风险优先数［41］等先后被提出，量化系统的故障严重程度和检测的困难度，进而定量分析系统的可靠性。

1.2 蒙特卡罗法

蒙特卡罗（Monte Carlo，MC）［42］法又称为模拟法，最早是由数学家J.Newman和S.Ulam提出的。它以概率统计理论为基础，借助于系统概率模型和随机变量仿真产生一些数学和技术问题来解决系统可靠性问题。蒙特卡罗仿真技术被认为在大型复杂网络的系统可靠性评估中起到重要作用。

文献［43］以神经网络为基础，结合蒙特卡罗仿真研究大型结构系统的可靠性。为了提高数据的统计效率和收敛性，降低计算的复杂度，基于交叉熵［44］的蒙特卡罗仿真被提出。该方法的基本思想是采样辅助重要性计算密度函数，利用优化过程最大限度的减少蒙特卡罗仿真的计算复杂度。文献［45］研究了基于元胞自动机的蒙特卡罗法系统可靠性分析方法，该方法不需要已知系统的最短路径或最小割集等信息，依然能够评估系统的可靠性，且分析结果比基于最短路径的蒙特卡罗法和基于最小割集的蒙特卡罗法要好。另外，文献［46］还将粒子群优化算法与蒙特卡罗模拟结合，解决了复杂网络系统可靠性计算的优化问题，最大限度地降低了计算成本。文献［47］利用支持向量机在计算速度方面的优势，将其与蒙特卡罗模拟结合，建立经验模型评估系统的可靠性。

1.3 综合法

综合法结合了解析法与蒙特卡罗法的优势，利用解析法分析构建系统可靠性模型，结合蒙特卡罗方法在模拟仿真方面的优势求解可靠性模型，降低计算难度，提高计算速度。

文献［48］提出时间故障树模型分析系统可靠性，利用蒙特卡罗仿真法加速模型的计算过程，其中系统的时间故障树模型能够表征时间与系统及部件故障次数之间的关系。文献［49］依据马尔科夫过程建立可靠性模型，并利用蒙特卡罗仿真求解系统可靠度，以提高计算效率。文献［50］认为动态故障树引入的动态门能够描述部件间的复杂关系，因此建立系统可靠性分析的动态故障树模型，并采用蒙特卡罗仿真求解模型。文献［51］继承故障树和马尔科夫模型的优势，定义一组新的分析系统可靠性模型——形式主义的布尔逻辑驱动马尔科夫过程。该模型在评估系统可靠性时，克服了马尔科夫法状态空间数量大以及故障树模型不能描述系统动态性等的缺点。

另外，在综合法中最常见的方式是基于Bayesian网络的系统可靠性分析方法。Bayesian网络模型［52］则利用贝叶斯在处理不确定理论方面的优势，结合最小路集或FTA建立系统贝叶斯网络，依据贝叶斯算法计算系统中各节点的故障概率，从而找出系统的薄弱环节，分析系统可靠性。

鉴于以往利用贝叶斯网络分析系统可靠性的研究中，贝叶斯网通常是由该领域的专家构建，可能存在不正确的推断，因此文献［53］提出一种利用历史数据，采用数据挖掘算法寻址部件间的关联关系，进而建立贝叶斯网模型最终对系统的可靠性进行分析。文献［54］提出一种基于贝叶斯统计的系统可靠性计算模型，它利用贝叶斯网络的传播和信息更新功能，由部件的信息预测系统的可靠性信息。文献［55］，基于贝叶斯网络的形式提出一种新的系统可靠性建模与分析的框架。通过分析时变的动态贝叶斯网络，找到一个合适的可靠性框架分析系统可靠性。文献［56］根据D-S证据理论在对不确定性认知过程中的优势，将D-S证据理论引入贝叶斯网络模型，并给出了改进后系统可靠性分析方法。Bai［57］首先构建贝叶斯网络，基于网络模型利用马尔科夫模型分析系统的可靠性。文献［58］结合系统的多故障序列和部件间极限状态相关性，运用贝叶斯网络评估系统结构的可靠性。

Bayesian网络模型能够较好的处理系统中不确定信息，且Bayesian网络直观形象，因此该模型是目前研究复杂系统可靠性应用最为广泛的方法之一。但是贝叶斯网络在构建时，存在两个条件独立的假设关系：①若已知父节点，任一节点与其非后代节点是条件独立的；②给定父节点、子节点以及子节点的父节点——马尔科夫覆盖，这个节点和网络中的所有其他节点是条件独立的，这两个假设条件并不适用于耦合关系复杂的系统。同时，在贝叶斯网络模型，计算的概率分布属于条件概率，而条件概率受人为主观因素影响较大，因此，对利用贝叶斯网络模型计算出的系统可靠性的客观性、真实性存在一定质疑。

1.4 网络法

针对解析法、蒙特卡罗法、综合法存在的本质问题，即系统的结构属性以及部件间的作用关系不能准确描述，基于网络理论研究系统可靠性的方法被提出。网络法的核心思想是将系统的可靠性问题与网络理论相结合，利用网络描述系统内部结构关系的优势，建立系统可靠性评价指标分析系统的可靠性。以Watts和Barabasi等人发现的小世界（Small-World）和无标度（Scale-Free）网络为标志，网络理论在系统可靠性的研究中受到广泛的关注，特别是在复杂网络系统中的应用。所谓复杂网络是指其拓扑特性满足特定的条件，例如服从小世界特性等。

网络系统的可靠性是指在正常运行的工况下，系统仍然保持原有网络功能的概率／能力。在研究复杂网络系统可靠性时，一般用连通可靠性来表示系统的可靠性，即网络的连通性越强，系统的可靠性越高。依据研究的侧重点不同，基于网络理论评价网络系统可靠性的指标也有所不同。杨孝平［59］等通过借鉴现实世界网络系统以及复杂网络系统可靠性的研究成果，归纳出评价复杂网络系统可靠性的指标体系，包括4个一级指标（即抗毁性、生存性、有效性、同步性），每个一级指标又包含若干个二级指标。但总的来说，现有的研究复杂网络系统可靠性的测度如图1所示。

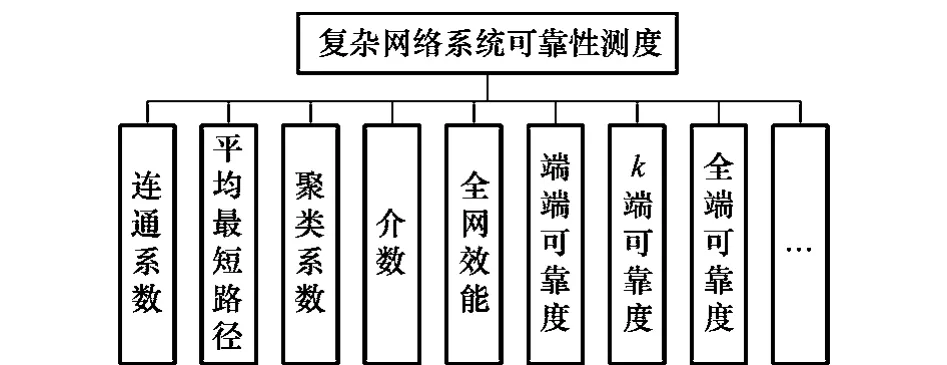
图1 复杂网络系统的可靠性测度指标

在对复杂网络可靠性的测度指标研究中，文献［60］给出聚类系数的定义，认为聚类系数表征了整个网络的平均的聚集程度，同时也可以衡量整个网络系统的连通性。文献［61］等提出评价网络抗毁性的指标测度——网络效能，对系统网络的可靠性进行分析。文献［62］等利用端端可靠度、全端可靠度、端可靠度等指标衡量整个系统网络的连通性，考察了复杂网络的生存性。文献［63］等针对复杂网络的特点，提出了评价复杂网络抗毁性的新测度——连通系数，利用连通系数研究网络的可靠性。文献［64］等根据复杂网络理论，对系统的故障进行定量分析，得出网络中介数较高的节点与度较高的节点同样重要，即介数高的节点对系统可靠性的影响也是十分重要的。另外，依据研究领域的特性，对评价系统可靠性指标的定义也略有不同。文献［65］根据公路网的特点，考虑子网数量、网络尺度和最短路径，定义评价整网连通可靠性指标连通系数。文献［66］基于电网系统中连接到发电机的节点数量占电网中节点总数量的比例，定义系统的可靠性指标。文献［67］将介数与度相结合，定义平均度介数来评价高速列车网的可靠性。

上述学者的研究主要是基于网络理论对系统拓扑结构可靠性的分析，忽略了系统中部件的基本属性。文献［68］在基于拓扑势的网络舆论模型中，首次同提出应同时考虑了网络的拓扑结构和节点自身属性，建立节点的重要性评价模型，并指出有效地结合表征网络拓扑结构和节点自身属性，以期更加全面准确的评估网络的性能是系统可靠性研究的未来发展方向。现有的考虑部件属性的系统可靠性研究，多是结合某一领域系统组份的特定性质展开的，如文献［69］将实际功率流以及线路流量分别作为电网系统中节点和边的属性，结合电网的拓扑结构研究电网系统的脆弱性。文献［70］将路网的容量、旅行时间与公路网络拓扑相结合，评价路网的可靠性与抗毁性。文献［71］结合轨道交通网，以实际的客流量为网络中节点属性，评估城市轨道交通网络的可靠性。

2 系统可靠性分析方法比较

4种系统可靠性分析方法优缺点比较如表1所示。

3 存在的问题与发展趋势

随着工业技术的进步，系统的复杂程度不断增加。解析法、蒙特卡罗法、综合法在描述系统拓扑结构特性以及部件之间作用关系等问题上的缺陷限制了其在复杂系统中的应用（见表1），而网络理论的出现为复杂系统可靠性的研究指明了方向。从目前的发展状况来看，基于网络理论的方法应用在系统可靠性研究中存在以下问题：一是基于网络理论的方法单纯对系统的拓扑可靠性进行分析，大多数研究并未考虑部件的可靠性属性对系统可靠性的影响；二是该方法大多数应用于复杂网络系统，对于一般的可用网络描述系统结构及行为特点的复杂系统应用较少。

表1 系统可靠性分析方法优缺点比较

综上所述，系统可靠性分析的发展趋势可大致概况为如下几点：

（1）复杂网络是复杂系统的抽象，现实中几乎所有的复杂系统都可以用网络模型来描述其内部结构关系，因此基于系统的网络特性，将其转化为网络模型，利用网络研究系统可靠性，尤其是复杂机电一体化的系统是未来可靠性发展方向。

（2）系统网络模型的构建。针对某一系统，如何选取节点和连接边，构建能够表征系统拓扑结构的网络模型是不仅是基于网络研究系统可靠性的基础，同时也是研究重点之一。

（3）现有基于网络的复杂系统可靠性研究大多是对系统拓扑结构可靠性的分析，部件的可靠性属性均未考虑［74］。因此，在系统拓扑网络模型的基础上，用来表征组成系统的各组份相互关系的拓扑结构和用来表征系统组份的节点可靠性属性／功能可靠性属性来构建评价系统可靠性的测度指标进而研究系统的可靠性，在国内尚属空白，但却是研究复杂系统可靠性的新思路。

4 结 论

综上所述，系统可靠性的分析方法仍然是可靠性工程中的研究热点与难点。传统的解析法、蒙特卡罗法、综合法已经无法满足对复杂系统的可靠性分析需求。随着网络理论的兴起及在复杂网络系统中的应用，为系统可靠性分析提供了新的研究方向。鉴于基于网络理论的复杂网络系统可靠性研究中存在的缺陷以及复杂系统的网络特性，对于复杂系统可靠性的研究，可将表征组成系统的各组份相互关系的拓扑结构和表征系统组份的节点可靠性属性相结合，定义新的可靠性测度指标，进而评价系统可靠性将是一个极具有研究价值的课题。

［1］Von Bertalanffy L.General system theory［J］.General Systems，1956，1（1）：11- 17.

［2］Bertalanffy L.General system theory：foundations，development，applications［M］.New York：Braziller，1968.

［3］Langefors B.Essaysin infology［M］.Lund：Studentlitteratur，1995.

［4］Miller J G.Living systems［M］.New York：McGraw Hill，1978.

［5］Qian X S.On systems engineering［M］.Changsha：Hunan Science and Technology Press，1982.（钱学森.论系统工程［M］.长沙：湖南科学技术出版社，1982.）

［6］Lee W S，Grosh D L，Tillman F A，et al.Fault tree analysis，methods，and applications-a review［J］.IEEE Trans.on Reliability，1985，34（3）：194- 203.

［7］Navarro J，Ruiz J M，Sandoval C J.Properties of coherent systems with dependent components［J］.Communications in Statistics—Theory and Methods，2007，36（1）：175- 191.

［8］Yannopoulos S，Spiliotis M.Water distribution system reliability based on minimum cut-set approach and the hydraulic availability［J］.Water Resources Management，2013，27（6）：1821- 1836.

［9］Noh Y，Choi K K，Du L.Reliability-based design optimization of problems with correlated input variables using a Gaussian Copula［J］.Structural and Multidisciplinary Optimization，2009，38（1）：1- 16.

［10］Ram M，Singh S B.Analysis of reliability characteristics of a complex engineering system under copula［J］.Journal of Reliability and Statistical Studies，2009，2（1）：91- 102.

［11］Ǒepin M，Mavko B.A dynamic fault tree［J］.Reliability Engineering&System Safety，2002，75（1）：83- 91.

［12］Byun S，Yang I，Song M G，et al.Reliability evaluation of steering system using dynamic fault tree［C］∥Proc.of the Intelligent Vehicles Symposium，2013：1416- 1420.

［13］Duan R X，Wan G C，Dong D C.A new assessment method for system reliability based on dynamic fault tree［C］∥Proc.of the Intelligent Computation Technology and Automation，2010：219- 222.

［14］Volovoi V.Modeling of system reliability Petri nets with aging tokens［J］.Reliability Engineering&System Safety，2004，84（2）：149- 161.

［15］Robidoux R，Xu H，Xing L，et al.Automated modeling of dynamic reliability block diagrams using colored petri nets［J］.IEEE Trans.on Systems，Man and Cybernetics-Part A：Systems and Humans，2010，40（2）：337- 351.

［16］Kavi K M，Sheldon F T，Shirazi B，et al.Reliability analysis of CSP specifications using Petri nets and Markov processes［C］∥Proc.of the 28th IEEE Hawaii International Conference on System Sciences，1995：516- 524.

［17］Garg H.Reliability analysis of repairable systems using Petri nets and Vague Lambda-Tau methodology［J］.ISA Transactions，2013，52（1）：6- 18.

［18］Azgomi M A，Entezari-Maleki R.Task scheduling modelling and reliability evaluation of grid services using coloured Petri nets［J］.Future Generation Computer Systems，2010，26（8）：1141- 1150.

［19］El Medhi A O，Leclercq E，Greah D L.Identification of stochastic and deterministic stochastic Petri net models for reliability analysis［J］.Proceedings of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2009，223（1）：13- 26.

［20］Pukite P，Pukite J.Markov modeling for reliability analysis［M］.New York：Wiley-IEEE Press，1998.

［21］Lisnianski A，Elmakias D，Laredo D，et al.A multi-state Markov model for a short-term reliability analysis of a power generating unit［J］.Reliability Engineering&System Safety，2012，98（1）：1- 6.

［22］Shier D R.Network reliability and algebraic structures［M］.Oxford：Clarendon Press，1991.

［23］Feng M L，Liu S Y.Reliability analysis of common channel signaling network under delay constraint［J］.Acta Electronica Sinica，2002，30（8）：1142- 1144.（冯海林，刘三阳.时延约束下公共信道信令网络的可靠性分析［J］.电子学报，2002，30（8）：1142- 1144.）

［24］Do Van P，Barros A，Bérenguer C.From differential to difference importance measures for Markov reliability models［J］.European Journal of Operational Research，2010，204（3）：513- 521.

［25］Binh P T T，Khoa T Q D.Application of fuzzy markov in calculating reliability of power systems［C］∥Proc.of the IEEE Transmission&Distribution Conference and Exposition，2006：1- 4.

［26］Dhople S V，Dominguez-Garcia A D.A parametric uncertainty analysis method for Markov reliability and reward models［J］.IEEE Trans.on Reliability，2012，61（3）：634- 648.

［27］Limnios N，Oprisan G.Semi-Markov processes and reliability［M］.Boston：Springer，2001.

［28］Gately W V，Williams R L.GO methodology—overview［R］.Palo Alto：Electric Power Research Institute，1978.

［29］Shen Z P，Wang Y，Huang X R.A quantification algorithm for a repairable system in the GO methodology［J］.Reliability Engineering&System Safety，2003，80（3）：293- 298.

［30］Chen Y，Ren Y，Liu L，et al.A new algorithm of GO methodology based on minimal path set［J］.AASRI Procedia，2012，3（10）：368- 374.

［31］Cai J，Zeng F.Reliability analysis of the supply chain based on the GO methodology［J］.Journal of Highway and Transportation Research and Development，2007，3：033.

［32］Zhong X J，Chen C，Yang J J.Reliability evaluation of phased mission system with common cause failures based on GO methodology［J］.Journal of Naval University of Engineering，2012，24（4）：86- 90.

［33］Wang R，Feng Z，Li P.Reliability analysis for power supply system in a typical reprocessing facility based on GO methodology［C］∥Proc.of the 21st International Conference on Nuclear Engineering，2013：V003T06A009- V003T06A009.

［34］Yang Z F，Wang J，Sha X F，et al.The brake system reliability evaluation of a type of Jiefang truck based on GO methodology［C］∥Proc.of the IEEE International Conference on Transportation，Mechanical，and Electrical Engineering，2011：1224- 1227.

［35］Li Z，Lu Z X，Liu J Q.Reliability analysis of nuclear power plant bus systems arrangement based on GO methodology［J］.Nuclear Power Engineering，2010，31（3）：69- 73，77.（李哲，鲁宗相，刘井泉.基于GO法的核电厂电气主接线系统可靠性分析［J］.核动力工程，2010（3）：69- 73，77.）

［36］Matsuoka T，Kobayashi M.GO-FLOW：a new reliability analysis methodology［J］.Nuclear Science and Engineering，1988，98（1）：64- 78.

［37］Stamatis D H.Failure mode and effect analysis：FMEA from theory to execution［M］.New York：Asq Press，2003.

［38］Xu K，Tang L C，Xie M，et al.Fuzzy assessment of FMEA for engine systems［J］.Reliability Engineering&System Safety，2002，75（1）：17- 29.

［39］Rhee S J，Ishii K.Using cost based FMEA to enhance reliability and serviceability［J］.Advanced Engineering Informatics，2003，17（3）：179- 188.

［40］Xiao N，Huang H Z，Li Y，et al.Multiple failure modes analysis and weighted risk priority number evaluation in FMEA［J］.Engineering Failure Analysis，2011，18（4）：1162- 1170.

［41］Chin K S，Chan A，Yang J B.Development of a fuzzy FMEA based product design system［J］.The International Journal of Advanced Manufacturing Technology，2008，36（7／8）：633- 649.

［42］Metropolis N，Ulam S.The Monte Carlo method［J］.Journal of the American Statistical Association，1949，44（247）：335- 341.

［43］Papadrakakis M，Lagaros N D.Reliability-based structural optimization using neural networks and Monte Carlo simulation［J］.Computer Methods in Applied Mechanics and Engineering，2002，191（32）：3491- 3507.

［44］González-Fernández R A，Leite da Silva A M.Reliability assessment of time-dependent systems via sequential cross-entropy Monte Carlo simulation［J］.IEEE Trans.on Power Systems，2011，26（4）：2381- 2389.

［45］Yeh W C，Lin Y C，Chung Y Y.Performance analysis of cellular automata Monte Carlo simulation for estimating network reliability［J］.Expert Systems with Applications，2010，37（5）：3537- 3544.

［46］Yeh W C，Lin Y C，Chung Y Y，et al.A particle swarm optimization approach based on Monte Carlo simulation for solvingthe complex network reliability problem［J］.IEEE Trans.on Reliability，2010，59（1）：212- 221.

［47］Rocco C M，Moreno J A.Fast Monte Carlo reliability evaluation using support vector machine［J］.Reliability Engineering &System Safety，2002，76（3）：237- 243.

［48］Ejlali A，Ghassem Miremadi S.FPGA-based Monte Carlo simulation for fault tree analysis［J］.Microelectronics Reliability，2004，44（6）：1017- 1028.

［49］Lewis E E，Böhm F.Monte Carlo simulation of Markov unreliability models［J］.Nuclear Engineering and Design，1984，77（1）：49- 62.

［50］Durga Rao K，Gopika V，Sanyasi Rao V V S，et al.Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment［J］.Reliability Engineering&System Safety，2009，94（4）：872- 883.

［51］Bouissou M，Bon J L.A new formalism that combines advantages of fault-trees and Markov models：boolean logic driven Markov processes［J］.Reliability Engineering&System Safety，2003，82（2）：149- 163.

［52］Langseth H，Portinale L.Bayesian networks in reliability［J］.Reliability Engineering&System Safety，2007，92（1）：92- 108.

［53］Doguc O，Ramirez-Marquez J E.A generic method for estimating system reliability using Bayesian networks［J］.Reliability Engineering&System Safety，2009，94（2）：542- 550.

［54］Mahadevan S，Rebba R.Validation of reliability computational models using Bayes networks［J］.Reliability Engineering& System Safety，2005，87（2）：223- 232.

［55］Boudali H，Dugan J B.A discrete-time Bayesian network reliability modeling and analysis framework［J］.Reliability Engineering&System Safety，2005，87（3）：337- 349.

［56］Simon C，Weber P，Evsukoff A.Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis［J］.Reliability Engineering&System Safety，2008，93（7）：950- 963.

［57］Bai C G，Hu Q P，Xie M，et al.Software failure prediction based on a Markov Bayesian network model［J］.Journal of Systems and Software，2005，74（3）：275- 282.

［58］Mahadevan S，Zhang R，Smith N.Bayesian networks for system reliability reassessment［J］.Structural Safety，2001，23（3）：231- 251.

［59］Yang X P，Yin C H.Research of reliability indexes of complex network［J］.Journal of Beijing Information Science and Technology University，2010，25（3）：92- 96.（杨孝平，尹春华.复杂网络可靠性评价指标［J］.北京信息科技大学学报：自然科学版，2010，25（3）：92- 96.）

［60］Wang X F，Li X，Chen G R.Complex network theory and its application［M］.Beijing：Tsinghua University Press Ltd.，2006.（汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社有限公司，2006.）

［61］Latora V，Marchiori M.Efficient behavior of small-world networks［J］.Physical review letters，2001，87（19）：1987- 1991.

［62］Sawionek B，Wojciechowski J，Arabas J.Synthesis of reliable networks in the presence of line failures［C］∥Proc.of the IEEE International Symposium on Circuits and Systems，2000：649- 652.

［63］Wu J，Tan Y J.Study on measure of complex network invulnerability［J］.Journal of Systems Engineering，2005，20（2）：128- 131.（吴俊，谭跃进.复杂网络抗毁性测度研究［J］.系统工程学报，2005，20（2）：128- 131.）

［64］Jiang H，Gao J，Chen F.System failure analysis based on complex network theory［C］∥Proc.of the Reliability and Maintainability Symposium，2009：176- 181.

［65］Deng Y J，Yang Y F，Ma R G.Highway network structure characteristics based on complex network theory［J］.China Journal of Highway and Transport，2010（1）：98- 104.（邓亚娟，杨云峰，马荣国.基于复杂网络理论的公路网结构特征［J］.中国公路学报，2010（1）：98- 104.）

［66］Xu S，Zhou H，Li C，et al.Vulnerability assessment of power grid based on complex network theory［C］∥Proc.of the Power and Energy Engineering Conference，2009：1- 4.

［67］Zhang J H，Cai Y Z，Xu X M，et al.Topological vulnerability of Chinese high speed rail network［C］∥Proc.of the Chinese Control Conference，2011：832- 837.

［68］Sun R，Luo W B.Review on evaluation of node importance in public opinion［J］.Application Research of Computers，2012，29（10）：3606- 3608.（孙睿，罗万伯.网络舆论中节点重要性评估方法综述［J］.计算机应用研究，2012，29（10）：3606- 3608.）

［69］Bompard E，Napoli R，Xue F.Analysis of structural vulnerabilities in power transmission grids［J］.International Journal of Critical Infrastructure Protection，2009，2（1）：5- 12.

［70］Zhao X Y，Shi A，Cong H Z.Traffic incident situation evaluation based on road network reliability of invulnerability［J］.Journal of Transportation Systems Engineering and Information Technology，2013，13（5）：79- 85.

［71］Yin Y，Lam W H K，Miller M A.A simulation-based reliability assessment approach for congested transit network［J］.Journal of Advanced Transportation，2004，38（1）：27- 44.

［72］Jiang H Q，Gao J M，Chen F M，et al.Vulnerability analysis to distributed and complex electromechanical system based on network property［J］.Computer Integrated Manufacturing Systems，2009，15（4）：791- 796.（姜洪权，高建民，陈富民，等.基于网络特性的分布式复杂机电系统脆弱性分析［J］.计算机集成制造系统，2009，15（4）：791- 796.）

［73］Zong G，Zhang Q，Liu W Z.Study on complexities in relational network of component maintenance for high-speed train in network perspective［J］.China Railway Science，2013，34（3）：105 -108.（宗刚，张起，刘文芝.网络视角下高速列车部件维修关系网络复杂性研究［J］.中国铁道科学，2013，34（3）：105- 108.）

［74］Zong G，Zhang C，Wang H S.Reliability study of the components for the traction system of high speed train based on complex network theory［J］.China Railway Science，2014，35（1）：94 -97.（宗刚，张超，王华胜.基于复杂网络理论的高速列车牵引系统部件可靠性研究［J］.中国铁道科学，2014，35（1）：94- 97.）

Current status and prospect for the methods of system reliability

JIA Li-min2，LIN Shuai1，2
（1.School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China；2.State Key Laboratory of Rail Traffic Control and Safety，Beijing Jiaotong University，Beijing 100044，China）

According to the structure of system and the reliability of components，how to analyze quantitatively system reliability is one of the important problems in reliability engineering.The methods of system reliability are summarized，and these methods are divided into analytical method，Monte Carlo method，the comprehensive method and the network method.Advantages and disadvantages of the four methods are analyzed and their application ranges are discussed.Finally，combined topological structure with reliability properties，new reliability measures are presented to evaluate system reliability，which is outlined as possible future directions.

system reliability；complex network；fault tree；state space

TB 114.3

A

10.3969／j.issn.1001-506X.2015.12.34

贾利民（196-3- ），男，教授，博士，主要研究方向为轨道交通控制与安全、交通安全测控工程、交通运输智能自动化、智能交通系统。

E-mail：lmjia＠bjtu.edu.cn

林 帅（198-7- ），女，博士研究生，主要研究方向为复杂机电系统可靠性与安全性。

E-mail：linshuai2013＠126.com

1001-506X（2015）12-2887-07

2014- 12- 19；

2015- 04- 29；网络优先出版日期：2015- 08- 17。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150817.1820.014.html

国家高技术研究发展计划（863计划）（2012AA112001）；轨道交通控制与安全国家重点实验室自主研究课题（I14K00451）资助课题