多分类概率极限学习机及其在剩余使用寿命预测中的应用

2015-06-05杜占龙李小民席雷平张金中刘新海

系统工程与电子技术 2015年12期

关键词：训练样本准确率概率

杜占龙，李小民，席雷平，张金中，刘新海

（1.军械工程学院无人机工程系，河北石家庄050003；2.总参通信工程设计研究院，辽宁沈阳110000）

由式（23）可得

中的B。因为

多分类概率极限学习机及其在剩余使用寿命预测中的应用

杜占龙1，李小民1，席雷平1，张金中2，刘新海1

（1.军械工程学院无人机工程系，河北石家庄050003；2.总参通信工程设计研究院，辽宁沈阳110000）

针对多分类极限学习机（extreme learning machine，ELM）缺乏概率输出能力问题，提出一种基于sigmoid后验概率映射和Lagrange成对耦合法的多分类概率ELM（multi-class probabilistic ELM，MPELM）。采用成对耦合法将多分类问题分解成多个二分类问题，利用sigmoid函数将二分类ELM输出映射成概率输出。为融合所有二分类概率输出，推导基于Lagrange乘子法的多分类概率计算公式，最终求解被预测样本分属不同类别的概率。将MPELM用于剩余使用寿命（remaining useful life，RUL）预测，实验结果表明，相比于多分类概率支持向量机（multi-class probabilistic support vector machine，MPSVM），MPELM耗时高于MPSVM，但MPELM所需优化参数少，预测精度高于MPSVM；与基于Hastie成对耦合法的MPELM相比，两者预测精度相近，本文MPELM的测试耗时较少。

极限学习机；后验概率；成对耦合法；故障预测

0 引言

____剩余使用寿命（remaining useful life，RUL）预测［1］作为故障预测与健康管理（prognostics and health management，PHM）重要组成部分，其预测结果是健康管理环节制定维修保障决策的重要依据，也是目前故障预测领域研究热点和难点。根据文献［2］分类方法，RUL预测主要包括模型法［3-4］和数据驱动法［5］。如文献［3］根据锂离子电池的退化模型，结合无迹粒子滤波预测电池的RUL。但是，实际设备通常难以建立准确的物理模型或者数学模型，限制了基于模型方法的应用范围，这种情况下，数据驱动法受到了更大关注。

数据驱动法预测RUL主要有基于退化轨迹相似性［5-6］，基于状态概率估计等方法［7］。其中，文献［5］根据同类设备性能退化数据，建立基于支持向量回归机（support vector regression，SVR）的退化轨迹模型，实现RUL预测。状态概率估计法根据已知设备的全寿命故障数据，确定每种退化状态对应的训练样本和RUL，建立具有概率输出能力的状态分类器，对于被预测设备，根据分类器得到的其分属不同退化状态的概率，连同每个状态对应的RUL计算其剩余使用寿命。如文献［7］利用概率支持向量机（support vector machine，SVM）预测轴承RUL。然而，SVM中的惩罚参数和核参数对预测性能影响较大，若参数选取不当，会降低RUL预测准确性。

极限学习机（extreme learning machine，ELM），是由文献［8］提出的一种单隐层前馈神经网络学习算法。理论上ELM可以提供良好的泛化能力，为解决回归和分类问题提供一种新途径，已经在时间序列预测［9］、故障诊断［10］等领域得到应用。文献［11］详细分析了ELM的分类性能，实验结果表明，ELM与SVM的分类精度相似，但ELM只需调整一个参数。与SVM需调整两个参数相比，ELM参数优化更易实现，同时能降低参数寻优过程复杂度。为利用ELM这一优势，将ELM应用于基于状态概率估计的RUL预测方法中，但是，传统的ELM不具备概率输出能力。

为此，本文利用Platt提出的sigmoid后验概率映射算法［12］，将ELM的数值型输出映射为概率输出。为克服sigmoid后验概率映射法只能用于二分类问题的局限性，采用成对耦合法融合所有的二分类概率输出。已有的成对耦合法包括投票法［13］、Hastie等人提出的方法［14］等，文献［15］对比了不同成对耦合法的多分类误差，实验结果表明Hastie法的分类准确率高于投票法。但是，Hastie法在计算多分类概率时需要进行多次迭代求解最优值，增加了运算时间。为此，本文将成对耦合法转化为二次规划求解最优值，推导基于Lagrange乘子法的多分类概率表达式。即对于D分类情况，首先将其分解成D（D－1）／2个二分类问题，利用ELM求解每个二分类情况的数值输出，并利用sigmoid后验概率映射将每个二分类的数值输出转化为概率输出；然后，采用Lagrange成对耦合法融合所有D（D－1）／2个概率输出值，最终得到D分类问题的概率输出。将多分类概率ELM（multi-class probabilistic ELM，MPELM）应用于设备的RUL预测中，某型无人机机载发射机参考时钟的RUL预测结果验证了本文方法的有效性。

1 极限学习机

ELM模型的输出可以表示为

式中，L为隐含层节点数目；ai∈Rn和bi∈R为ELM隐含层的参数；βi∈Rm为第i个隐节点到输出节点的权值；G（ai，bi，x）表示第i个隐节点的输出函数，若隐含层为加性隐节点，则

式中，ai为连接第i个隐节点的输入权值；bi为第i个隐节点的偏差；g（·）为激活函数。

给定由N组数据组成的训练样本集｛（xl，tl）1，其中xl∈Rn为输入向量，tl∈Rm为对应的期望输出，即

将式（3）改写成矩阵形式，即

式中

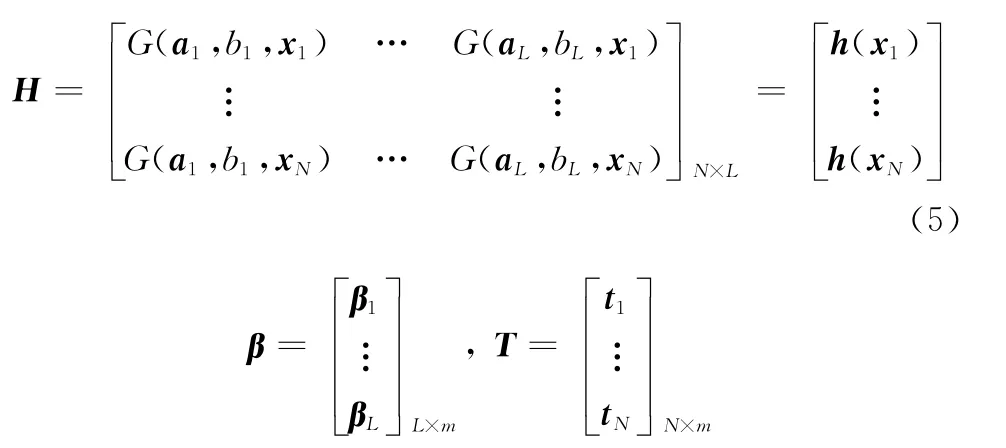
在ELM学习算法中，ai和bi均为随机产生，只有β利用｛（xl，tl）计算得到。为了提高ELM泛化性能，在解决分类问题时，可以将求解β看成如下优化问题［11］：

式中，训练误差εl用于避免过拟合现象；λ为惩罚因子。根据Karush-Kuhn-Tucker定理［11］，式（6）可以转化为双重优化问题。

由式（7）可以得到β的最优解［11］为

对被预测样本x的二分类问题，决策方程为

对被预测样本x的多分类问题，决策方程为

式中，fi（x）为第i个输出节点的输出，且f（x）＝［f1（x），…，fm（x）］T。

2 MPELM

2.1 Sigmoid函数概率映射

对于分类问题，传统的ELM只能输出类别结果，即给出被预测样本属于某一类别，而缺乏概率输出能力，即样本分属于不同类别的概率。为了将ELM的输出转化为概率形式，采用Platt提出的基于sigmoid函数的后验概率映射法［12］，将ELM的输出值转化为后验概率。对于二分类问题｛＋1，－1｝，映射函数可以表示为

式中，f＋1（x）为ELM对应于类别标签为＋1的输出，P（t＝－1｜x）＝1－P（t＝＋1｜x）。对于参数A＋1和B＋1的确定，需要根据训练样本｛（xl，yl）求解以下对数似然函数最小值：

式中

式中，N＋和N－分别为标签为＋1和－1的训练样本数目。采用Levenberg-Marquardt算法求解式（12）中的A＋1和B＋1，具体算法流程可以参考文献［12］中的附录部分。

2.2 成对耦合法

Platt提出的Sigmoid函数后验概率映射法仅适用于二分类问题，为了解决D分类问题，采用成对耦合法将其分解成D（D－1）／2个二分类问题，其中D＞2为类别个数。对于由第i类别和第j类别组成的二分类问题，记rij为输入样本x属于第i类别的概率值，即

为了最终计算输入向量x属于不同类别i的概率pi，如式（16）所示，需要融合D（D－1）／2个二分类概率值rij。

融合D（D－1）／2个rij求解pi可以等效为求解以下方程的最小值［16］：

文献［16］已经证明式（17）中任意优化后得到的p＝｛p1，…，pi，…，pD｝均能满足pi≥0，i＝1，2，…，D。则式（17）可以变成二次规划问题：

式中

式中，Qij为式（18）中Q的第i行j列元素，i，j＝1，2，…，D。利用Lagrange乘子法求解式（18），则Lagrange函数为

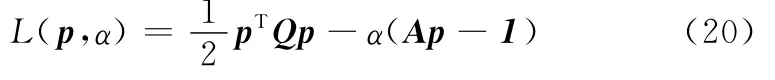
令pL（p，α）＝0，αL（p，α）＝0，得到方程组

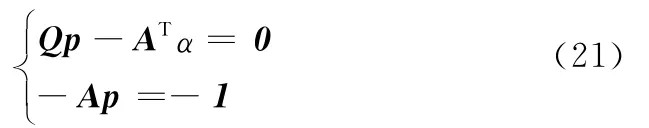
将式（21）写成分块矩阵形式

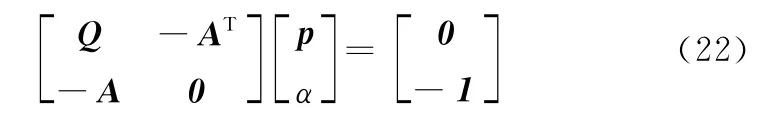
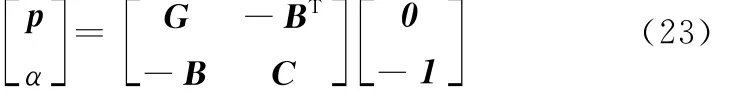
由式（23）可得

中的B。因为

则

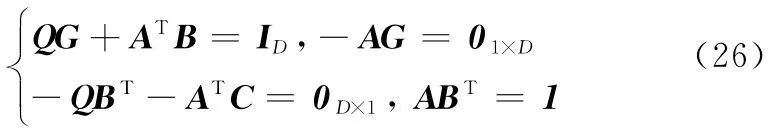
对式（26）进行求解，得

最后，将BT的值作为输入向量x属于不同类别i的概率集合｛p1，…，pi，…，pD｝。

2.3 MPELM算法流程

给定训练样本集｛（xl，tl），其中xl∈Rn为输入向量，tl∈｛1，…，D｝为类别标签。则整理得多分类概率极限学习机算法步骤如下。

步骤1将｛（xl，tl）分解成D（D－1）／2组二分类｛i，j｝训练样本，其中由类别i和j组成的训练样本为｛（xl， t′l），t′l∈｛i，j｝。若t′l＝i，则令＝1，若t′l＝j，则令＝－1。从而将｛i，j｝类训练样本变成｛（xl，），i，j＝1，2，…，D，且i≠j。

步骤2 将｛（xl）｝代入式（8）计算其对应的ELM输出权重βij，按式（28）计算xl对应的ELM输出fij（xl）。式中，h（xl）按式（5）计算。

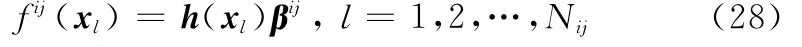
步骤3 利用｛fij（xl）｝求解｛i，j｝类对应的参数Aij和Bij，l＝1，2，…，Nij。

式中，Ni和Nj分别为属于类别i和类别j的训练样本个数，将pl和yl代入式（12）计算Aij和Bij。

步骤4 对于被预测样本的输入向量x，计算其与｛i，j｝类对应的ELM输出fij（x）和概率输出rij，i，j＝1，2，…，D，且i≠j。

步骤5 利用Lagrange乘子法求解多分类概率。即将rij代入式（19）计算Q，然后将Q和式（19）中的A代入式（27）计算B，则BT为被预测样本的输入向量x分属于所有D个类别的概率｛p1，…，pD｝。

3 RUL预测

根据设备的历史全寿命数据，采用状态概率估计法预测RUL，其中利用本文提出的MPELM估计当前时刻设备分属于不同退化状态的概率，连同由历史数据确定的不同退化状态对应的剩余使用寿命，计算当前设备的RUL。基于多分类概率极限学习机的RUL预测算法如下。

（1）利用历史全寿命数据组成训练样本｛（xl，tl）｝，其中xl为能反映设备退化程度的故障特征，tl∈｛1，…，D｝为不同退化状态标签，D为退化状态数目。根据｛（xl，tl）｝训练MPELM。

（2）对于被预测设备，将其当前时刻k的故障特征xk代入训练好的MPELM，计算设备属于退化状态i（i＝1，2，…，D）的概率pi，k。

（3）k时刻RUL的预测按照下式计算：

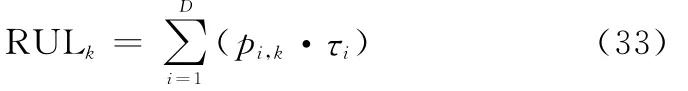
式中，τi为根据历史全寿命数据确定的退化状态i对应的RUL。

值得注意的是，在RUL预测中，当前设备的寿命数据和历史设备往往存在差异，可能将不属于任何已知类别的数据归到错误的一类，导致RUL预测失效。为克服此问题，可以参考文献［18］的方法，即利用每种退化类别标签对应的故障特征训练一个OCSVMj（一类支持向量机），j＝1，2，…，D。对于当前时刻k的故障特征xk，分别将xk送入D个OCSVMj，并判断xk是否属于OCSVMj。若结果为xk至少属于一种OCSVMj，说明xk属于已知的退化状态，可以按照本文提出的MPELM预测RUL。反之，说明xk不属于已知的退化状态，可能导致RUL预测无效。

4 实例分析

4.1 实验数据

利用某型无人机机载发射机故障注入实验台的故障数据验证本文方法在RUL预测中的有效性，实验台主要由发射机故障注入样机、计算机、程控测量仪器和直流电源组成，如图1所示。

图1 机载发射机故障注入实验台

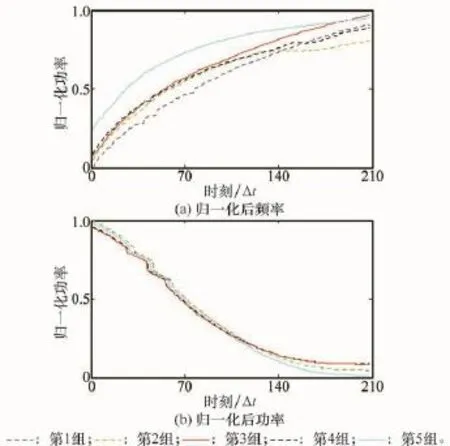
图2 参考时钟缓变故障下输出频率和功率

4.2 参数选择

为证明本文方法有效性，采用3种方法：多分类概率支持向量机（MPSVM）、基于Hastie成对耦合法的多分类概率ELM（Hastie-MPELM）、本文提出的基于Lagrange成对耦合法的多分类概率ELM（Lagrange-MPELM），作为设备退化状态分类器，预测发射机RUL。其中，方法1采用LIBSVM工具箱中提供的概率SVM，为了求解式（16）的概率，方法2采用Hastie方法［14］融合不同二分类概率输出、方法3采用本文推导的Lagrange乘子法融合二分类概率输出。式（2）中ELM激活函数g（·）选为sig。实验环境为Windows XP系统，酷睿i3处理器（主频3.3 GHz），3.4 GB内存，运行软件为MATLAB R2011b。

对于MPSVM，惩罚参数C和核参数γ对分类性能影响较大；对于Hastie-MPELM和Lagrange-MPELM，式（8）中的参数λ和式（3）中的隐节点数目L需要人为确定。另一方面，退化状态数D同样影响着RUL预测的准确性。

4.2.1 λ和L对MPELM的影响

对于两种MPELM，λ和L需要人为确定。分别令两个参数λ＝｛2－24，2－23，…，224，225｝，L＝｛100，200，…，2 000｝，利用网格搜索法计算每一对λ和L对应的RUL预测准确率，其中第1～3组数据用于训练两种MPELM，利用第4组数据计算RUL准确率，如式（34）所示。同理，对MPSVM，分别令C和γ＝｛2－24，2－23，…，224，225｝，计算每一对C和γ对应的RUL预测准确率。以退化状态数为4时的情况为例，3种方法的RUL预测准确率如图3所示。

式中，Ntest＝208为测试样本的采样点数；^ξk为RUL的预测值；ξk为RUL的实际值。

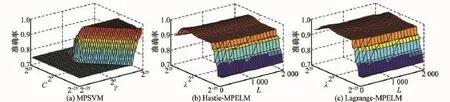
图3 不同参数对应的RUL预测准确率

由图3可知，对于两种MPELM，只要λ选择恰当，L对RUL准确性影响较小；而对于MPSVM，参数C和γ对RUL准确性影响较大。与MPSVM需要同时优化两个参数C和γ相比，两种MPELM只需对λ进行优化，从而简化参数寻优过程。因此，在本文下面的参数寻优过程中，固定L＝1 000，分别令Hastie-MPELM和Lagrange-MPELM中的λ、MPSVM中的C和γ在｛2－24，2－23，…，224，225｝中搜索最优参数。

4.2.2 参数优化结果

由4.2.1节分析结果可知，两种MPELM的λ，MPSVM的C和γ需人为确定。此外，不同退化状态数目D同样影响着RUL的预测准确性。为了确定合理的D，选择已知的一组故障数据作为评价标准，计算不同D下该组数据的RUL预测准确率，选择最大准确率对应的D作为选定的退化状态个数。对于本实验，选择第4组数据用于优化D，分别令D＝2，3，…，10，D在每种取值下，令λ在｛2－24，2－23，…，224，225｝中变化，λ每取一次值，利用第1～3组数据组成的训练样本建立一个Lagrange-MPELM，然后计算其对第4组数据的RUL预测准确率，取所有λ中RUL预测准确率最大值作为状态数为D时的准确率，如图4所示。可以看出，当D＝4时，RUL准确率最大，为此，选取退化状态数目为4。其中，第1～3组故障数据作为训练样本的抽取方式及其对应的RUL如表1所示，利用（208Δt－Ti）／207Δt计算不同退化状态对应的RUL，Ti为状态i对应的平均工作时间。

图4 不同退化状态数对应的RUL预测准确率

表1 退化状态数为4时的训练样本

固定L＝1 000，分别令两种MPELM中的λ、MPSVM中的C和γ在｛2－24，2－23，…，224，225｝中搜索最优值。对于每一次Hastie-MPELM和Lagrange-MPELM中λ的搜索值，根据训练样本（见表1）建立MPELM模型，利用第4组故障数据计算RUL预测准确率，选择RUL预测准确率最大时对应的λ作为预测RUL的最优参数，如表2所示。同理，MPSVM的最优C和γ如表2所示。3种方法搜索最优参数的耗时如表2所示，与MPSVM需要同时优化2个参数C和γ相比，2种MPELM只需要优化1个参数λ，所以2种MPELM的寻优耗时少于MPSVM。

表2 最优参数及寻优耗时

4.3 RUL预测

分别利用3种方法预测第4、5组数据的RUL，训练样本和状态分类器参数如表1和表2所示。其中，参数优化利用第4组数据，本文称其为已知测试样本，第5组故障数据没有参与分类器的训练和参数优化过程，本文称其为未知测试样本。本文提出的Lagrange-MPELM对第4、5组故障数据分属于4种退化状态的概率估计值如图5所示，发射机在起始阶段属于状态1的概率接近100%，随着退化过程延续，属于状态1的概率逐渐降低，属于状态2的概率增加，直至最后属于状态4的概率变为最大，其中相邻状态间曲线的重叠主要由不同样本间的差异性造成。

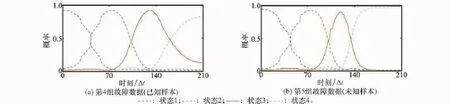
图5 Lagrange-MPELM对测试样本分属于不同退化状态的概率估计

通过计算不同时刻测试样本分属于4个退化状态的概率（表3为部分时刻3种方法对第5组数据的概率输出值），连同表1所示的不同退化状态对应的RUL，利用式（33）计算所有208个时刻测试数据的RUL，3种方法对第4、5组测试样本的RUL预测值和预测误差绝对值分别如图6和图7所示。

表3 3种方法对第5组数据的部分时刻概率输出（k=4Δt，78Δt，130Δt，204Δt）

图6 第4组数据（已知样本）预测结果

进行50次蒙特卡罗仿真，3种方法的RUL预测准确率、训练耗时和测试耗时如表4所示，其中RUL预测准确率按式（34）计算，训练耗时是指利用表1所示的训练样本和表2所示的最优参数训练分类器的时间，测试耗时是指利用训练好的分类器计算第4组或第5组的208个故障数据对应的RUL所需的时间。

由图6、图7和表4可知，对于已知的测试样本（第4组故障数据），3种方法的预测准确率相差不大，但是对于未知的测试样本（第5组故障数据），两种MPELM的预测精度高于MPSVM，相比之下，Lagrange-MPELM的预测精度略高于Hastie-MPELM。在模型训练过程中，两种MPELM方法需要对式（12）进行优化，在模型测试过程中，两种MPELM方法需要融合所有的二分类概率输出，因此，两种MPELM方法的训练耗时和测试耗时高于MPSVM。在模型测试阶段，Hastie-MPELM需要通过多步迭代求解所有二分类融合的最优值，而Lagrange-MPELM利用式（27）即可求得最优值，所以Lagrange-MPELM的测试耗时低于Hastie-MPELM。

图7 第5组数据（未知样本）预测结果

表4 RUL测试准确率和耗时

5 结论

本文根据极限学习机在多分类问题中泛化能力强、所需优化参数少这两个优点，提出基于多分类概率极限学习机的剩余使用寿命预测算法。利用无人机发射机的故障数据进行实验验证，结果表明，在模型参数优化方面，与MPSVM需要优化参数C和γ相比，MPELM只对参数λ敏感，所以MPELM方法在参数寻优耗时上少于MPSVM；在RUL预测性能方面，MPELM的训练和测试耗时高于MPSVM，但是MPELM的预测精度优于MPSVM。与Hastie-MPELM相比，本文提出的Lagrange-MPELM测试耗时更低。

［1］Banjevic D.Remaining useful life in theory and practice［J］.Metrika，2009，69（2）：337- 349.

［2］Kamal M，Diego A，Tobon M，et al.Remaining useful life estimation of critical components with application tobearings［J］.IEEE Trans.on Reliability，2012，61（2）：292- 302.

［3］Miao Q，Xie L，Cui H G，et al.Remaining useful life prediction of lithiumion battery with unscented particle filter technique［J］.Microelectronics Reliability，2013，53（6）：805- 810.

［4］Hu C，Jain G，Gorka T.Method for estimating capacity and predicting remaining useful life of lithiumion battery［J］.Applied Energy，2014，126（1）：182- 189.

［5］Benkedjouh T，Medjaher K，Zerhouni N，et al.Remaining useful life estimation based on nonlinear feature reduction and support vector regression［J］.Engineering Applications of Artificial Intelligence，2013，26（7）：1751- 1760.

［6］Liu J B，Djurdjanovic D，Ni J，et al.Similarity based method for manufacturing process performance prediction and diagnosis［J］.Computers in Industry，2007，58（6）：558- 566.

［7］Kim H E，Tan A C C，Mathew J，et al.Bearing fault prognosis based on health state probability estimation［J］.Expert Systems with Applications，2012，39（5）：5200- 5213.

［8］Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：theory and applications［J］.Neurocomputing，2006，70（1／3）：489- 501.

［9］Kamran J，Rafael G，Noureddine Z.SW-ELM：a summation wavelet extreme learning machine algorithm with a priori parameter initialization［J］.Neurocomputing，2014，123（1）：299- 307.

［10］Yuan X，Chen Y J，Zhu Q X.An extension sample classification-based extreme learning machine ensemble method for process fault diagnosis［J］.Chemical Engineering&Technology，2014，37（6）：911- 918.

［11］Huang G B，Zhou H M，Ding X J，et al.Extreme learning machine for regression and multiclass classification［J］.IEEE Trans.on Systems，Man，and Cybernetics-Part B：Cybernetics，2012，42（2）：513- 529.

［12］Platt J C.Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods［J］.Advances in Large Margin Classifiers，1999，10（3）：61- 74.

［13］Miguel M，Eddy M.Improved pairwise coupling classification with correcting classifiers［C］∥Proc.of the 10th European Conference on Machine Learning，1998：160- 171.

［14］Trevor H，Robert T.Classification by pairwise coupling［J］.The Annals of Statistics，1998，26（2）：451- 471.

［15］Mirosław K，Waldemar W.New variants of pairwise classification［J］.European Journal of Operational Research，2009，199（2）：512- 519.

［16］Wu T F，Lin C J，Weng R C.Probability estimates for multiclass classification by pairwise coupling［J］.Journal of Machine Learning Research，2004，5（1）：975- 1005.

［17］Yan X，Li Y S，Gao S，et al.Fast method to enforce the passivity of macromodels for the admittance matrix［J］.Journal of Xidian University（Natural Science），2011，38（1）：153- 158.（闫旭，李玉山，高崧，等.一种实现导纳矩阵宏模型无源性的快速方法［J］.西安电子科技大学学报（自然科学版），2011，38（1）：153- 158.）

［18］Wang J C，Shan G L，Duan X S，et al.Analog circuit fault diagnosis method combining OCSVM［J］.Computer Engineering，2012，38（4）：170 -173.（王俭臣，单甘霖，段修生，等.结合OCSVM的模拟电路故障诊断方法［J］.计算机工程，2012，38（4）：170- 173.）

Multi-class probabilistic extreme learning machine and its application in remaining useful life prediction

DU Zhan-long1，LI Xiao-min1，XI Lei-ping1，ZHANG Jin-zhong2，LIU Xin-hai1
（1.Department of UAV Engineering，Ordnance Engineering College，Shijiazhuang 050003，China；2.Communication Engineering Design and Research Institute of PLA General Staff Headquarters，Shenyang 110000，China）

To solve the problem that multi-class extreme learning machine（ELM）lacks the ability of probabilistic output，a multi-class probabilistic ELM（MPELM）algorithm is presented based on the combination of sigmoid posterior probability mapping and Lagrange pairwise coupling.Firstly，after separating the multi-class problem into the type of two-class problem by pairwise coupling，each two-class ELM output is transformed to the probabilistic output by sigmoid function.Then，the multi-class probabilistic computing expression is deduced based on the Lagrange multiplier method，which is utilized to fuse all two-class probabilistic outputs.Finally，the probabilistic results of predicted samples belonging to different classes are obtained.The proposed MPELM is applied to remaining useful life（RUL）prognosis.The experiment results show that，compared with multi-class probabilistic support vector machine（MPSVM），though time consuming of the proposed MPELM is higher than MPSVM，less optimized parameter is required while higher forecasting accuracy is achieved by MPELM.The predicting accuracy of the proposed MPELM is similar to MPELM based on the Hastie pairwise coupling（Hastie-MPELM）algorithm.But test time consuming of the proposed MPELM is less than Hastie-MPELM.

extreme learning machine（ELM）；posterior probability；pairwise coupling；fault prediction

TP 206＋.3

10.3969／j.issn.1001-506X.2015.12.18

杜占龙（198-6- ），男，博士研究生，主要研究方向为故障诊断和故障预测。

E-mail：dzl_1986＠163.com

李小民（196-8- ），男，教授，博士，主要研究方向为电子系统性能检测与故障诊断。

E-mail：lxmfy2000＠263.net

席雷平（1979- ），男，讲师，博士，主要研究方向为检测技术、自动目标识别。

E-mail：research_mail＠sina.cn

张金中（198-5- ），男，工程师，主要研究方向为通信设备检测诊断。

E-mail：mec_edu＠126.com

刘新海（198-8- ），男，工程师，主要研究方向为自动测试技术、自动测试理论。