基于多任务学习方向图可重构稀疏阵列天线设计

2015-06-05李龙军王布宏夏春和沈海鸥

系统工程与电子技术 2015年12期

关键词：布阵多任务旁瓣

李龙军，王布宏，夏春和，沈海鸥

（1.空军工程大学信息与导航学院，陕西西安710077；2.北京航空航天大学计算机学院，北京100191）

基于多任务学习方向图可重构稀疏阵列天线设计

李龙军1，2，王布宏1，夏春和2，沈海鸥1

（1.空军工程大学信息与导航学院，陕西西安710077；2.北京航空航天大学计算机学院，北京100191）

方向图可重构天线能够根据实际需要实时改变阵列天线的方向图，稀疏天线阵在满足方向图要求的前提下可以有效降低天线设计的复杂度。提出了一种基于多任务学习的方向图可重构稀疏阵列天线设计方法。将稀疏阵列优化设计及其方向图综合问题转换成为稀疏矩阵的线性回归问题，利用多任务学习能同时对多个相关任务优化学习的特性，建立了多个方向图联合赋形的多任务学习模型。通过迭代收缩阈值的方法，对多任务学习问题进行优化求解，使得阵列天线能够使用更少的阵元实现多个方向图的重构。仿真结果表明，该方法可以生成相同阵列结构的稀布天线阵，并通过动态改变其权值向量，实现多个方向图的精确赋形。

可重构方向图；稀疏阵列；多任务学习；方向图赋形

0 引言

随着无线电通信技术的不断发展，需要阵列天线能够实现通信、导航、定位等多种目标任务，这对有限载机平台空间和载荷，天线布阵均提出了严峻的挑战［12］。适应现代雷达通信系统综合化的需要，通过发展多功能阵列天线来减少阵列天线的数量，已成为阵列天线发展的必然趋势。作为多功能阵列天线的一种，方向图可重构阵列天线可以采用同一个天线阵列，通过动态实时改变天线单元的权值向量，使其方向图能够动态可重构，实现之前由多个阵列才能完成多个目标任务。采用方向图可重构的阵列天线不但可以减少阵列天线的单元数量，降低系统的制造成本，还能有效避免各种机载电子系统的电磁兼容问题。

方向图可重构阵列天线技术作为一种新的阵列天线技术，受到国内外的广泛关注，目前国内外已有科研人员对其做了研究。文献［3- 5］利用遗传算法和粒子群算法对权值幅值确定的均匀阵列天线的激励相位进行优化，设计了笔形波束和平顶波束方向图可重构的均匀阵列天线。文献［6］利用改进的遗传算法实现了对等间隔布阵的阵列天线方向图旁瓣的可重构。文献［7］通过对阵列天线馈电网络权值的控制实现了方向图可重构的等间隔均匀布阵的直线阵列天线设计。文献［8］将遗传算法和矩量法相结合，设计了矩形环可重构天线模型，并对其性能进行了分析，但并没有给出基于该单元设计的方向图可重构阵列天线布阵方法。文献［9］设计制作了一种用于无线通信移动终端的方向图可重构的阵列天线，并实现了8个不同方向的波束指向。文献［10］提出了一种基于全波和网络混合的可重构天线仿真分析方法，并验证了矩形环可重构阵列天线具有频率可重构和方向图可重构的功能。综上所述，目前研究还处于起步阶段，且研究都是以等间隔布阵的阵列天线作为研究对象，对于大型阵列天线，存在阵元数目过多，机载平台体积过大，重量增加，同时馈电网络设计复杂且成本太高的问题。稀疏布阵是指使用少量的天线单元，采用非均匀的单元设置，充分利用阵列天线的孔径，获得较窄的方向图主瓣波束宽度和较高的分辨能力。阵列天线稀疏布阵有利于系统成本的降低和单元互耦效应的有效抑制。如何进一步减小阵元数量，在对均匀阵列天线进行稀疏布阵的同时，通过改变阵元权值向量来实现阵列天线方向图的可重构，目前在国内外还没有相关研究报道。

多任务学习（multi-task learning，MTL）是指利用任务之间的相关性，对多个任务目标同时学习的特征学习方法［1117］。在之前的研究中多任务学习的方法常常被用来进行目标图像的特征识别［1819］，本文将阵列天线稀疏优化问题转换成为稀疏矩阵的线性回归问题，以不同功能的方向图作为目标任务进行稀疏学习，建立了多任务学习的稀疏线阵方向图可重构模型。利用迭代阈值收敛的方法以及分块坐标下降法对模型进行求解，实现了稀疏直线阵列天线对不同方向图的重构设计。相对于其他的方法，该方法能够利用更少的单元对多个不同功能的方向图进行重构，且得到的方向图与等间隔均匀布阵的阵列天线的方向图有近似一致的重构效果。本文的主要工作如下：

（1）通过多任务学习目标函数的分析，建立了方向图可重构稀疏阵列天线的多任务学习模型。

（2）利用l1／l2范数作为惩罚函数，以稀疏参数控制阵列激励的非零行数，利用最陡梯度下降法，结合迭代阈值搜索的方法，对稀疏阵列天线位置及其激励进行了优化求解。

（3）通过仿真实验证明，利用基于多任务学习的稀布阵列方向图可重构模型，在稀疏等间隔分布的阵列天线同时，可以对切比雪夫笔形波束（Chebyshev）、平顶波束（Flattop）和余割平方波束（Cosecant）方向图进行理想重构。

1 多任务学习机制

多任务学习方法是单任务学习的一个延伸。相对于单任务学习独立学习完成任务的方式，多任务学习联合多个训练数据同时完成最后的任务学习。其示意图如图1所示。

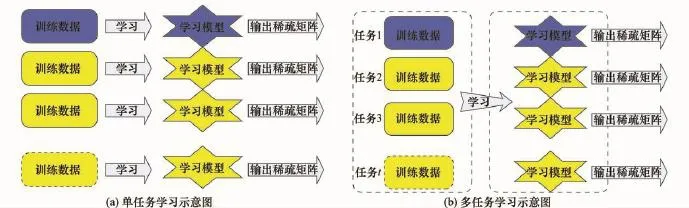
图1 稀疏学习示意图

其数学模型可表示为

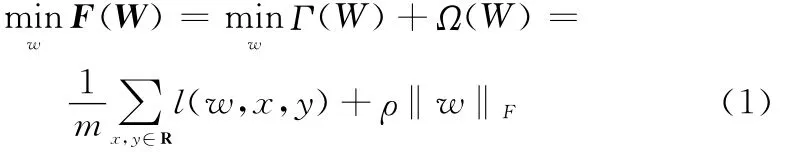
从图1中可知，相对于单任务学习，多任务学习能同时对多个任务进行稀疏学习，通过对正则化项范数值F和正则化参数ρ的选择，可以确定权值的输出。而且单任务学习的每次任务的学习不能保证输出的权值向量在相同位置处出现零值，对需要输出的权值向量具有相同结构的要求，单任务学习模型并不能满足，因此单任务学习模型并不能用于对方向图可重构的稀疏布阵天线的优化设计。相对于单任务学习，多任务学习采用的是并行关联稀疏学习的方法，以此能够充分利用计算资源，节省运算时间，提高模型的运算效率。

2 方向图可重构稀疏阵列天线的多任务学习模型

一个阵元数为N，阵元间距为λ／2，λ为入射信号的波长，入射方位角为θ的等间隔布阵的直线阵列天线（本文以均匀线阵的稀疏化为例，但方法易于扩展到其他阵列形式），当阵元均为理想的全向性单元时，其方向图可表示为

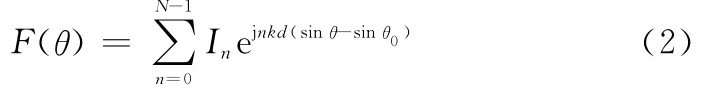
式中，k＝2π／λ；λ为信号波长；θ0决定阵列方向图主瓣的方向。令θ0＝0，u＝sinθ。则式（2）可表示为

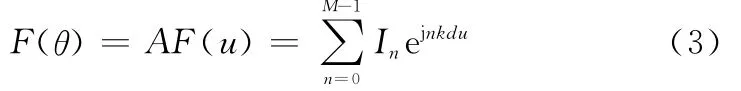
若将N元的均匀阵列天线孔径均分为M等分的栅格，即每个栅格的长度为Nλ／2M，对天线方向图进行D点采样，则此时线阵方向图赋形问题可以表示为

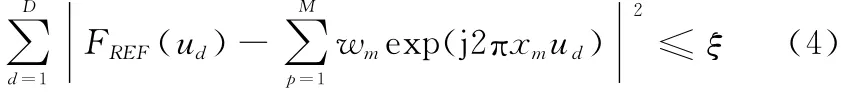
式中，ξ为容忍度；wm和xm（单位为波长λ）为第m个阵元的激励与位置；FREF（ud）为期望方向图的D点采样值。式（4）可以等价为最小二乘优化问题，即

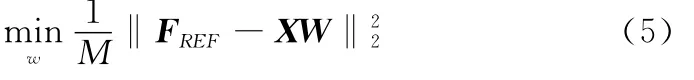
式中，‖·‖2为l2范数；W＝wn（n＝1，2，…，P）为待求的阵元激励向量；FREF为期望方向图的D点样本矩阵；X为导向矢量构成的矩阵，表示为

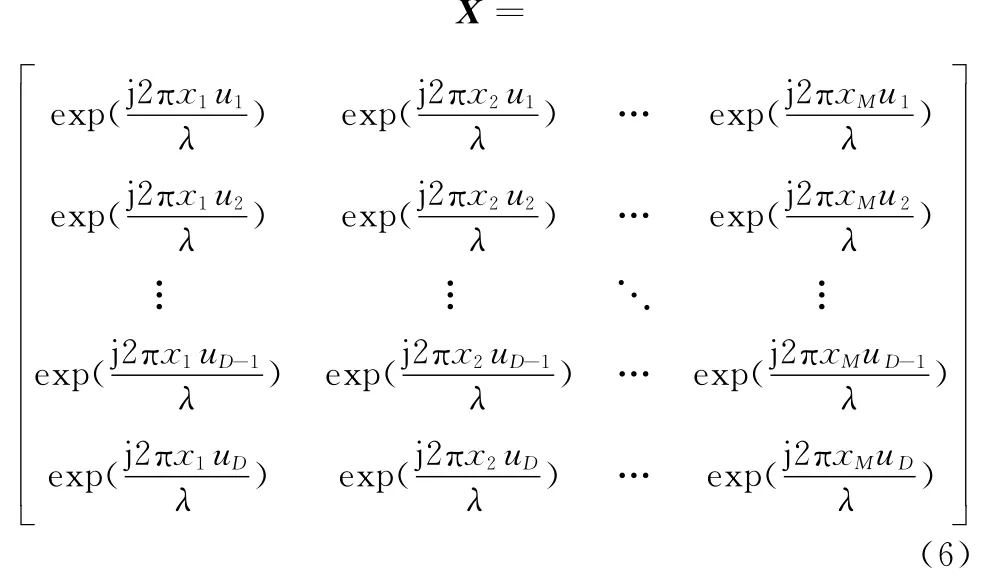
对于N元的均匀等栅格分布的线阵，其方向图可重构的多任务稀疏学习模型可以表示为

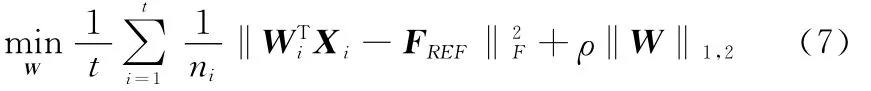
式中，t为需要重构的期望方向图的类型数目；W为待求的阵元激励矩阵向量；X为阵列天线的导向矢量；FREF为期望方向图；ρ为稀疏参数，也称为正则化参数。它是用来控制函数的逼近程度和稀疏度的参数，ρ值越大，W非零行向量越少，阵列天线的稀疏率越高，同时，方向图逼近效果越差，当ρ减小时，天线方向图逼近程度越好，但稀疏率随之减小。‖·‖1，2为l1／l2范数，表示为

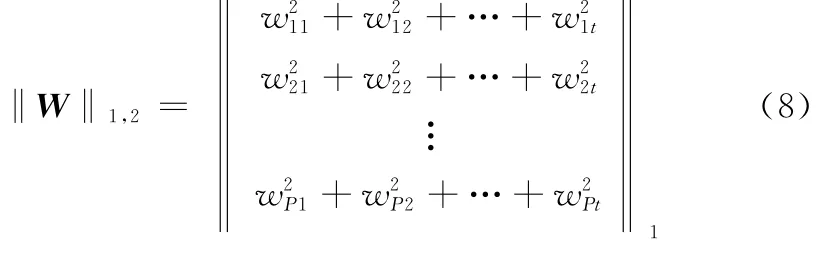
选择l1／l2范数作为模型的正则化项可以保证每个学习任务的权值的零值出现在同一行的位置，这就能保证模型在对同一个等栅格布阵的直线阵列天线的多个不同功能的方向图进行稀疏学习时，稀疏后的阵列天线结构是一致的，只是阵元的激励值发生变化。方向图可重构的阵列天线多任务稀疏学习模型如图2所示。从图2中可以看出，模型能对多个不同功能的方向图进行学习，且学习后的阵列单元的位置结构一致。多任务学习能够选择很少一部分权值的非零行向量实现对期望方向图的线性回归，使得模型能够在对阵列天线稀疏的同时，通过动态改变稀疏后阵列天线单元的激励值实现多个不同功能方向图的重构设计。

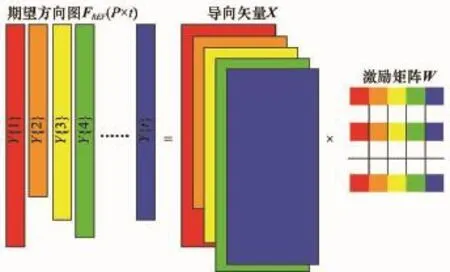
图2 方向图综合的多任务学习模型

3 方向图可重构稀疏阵列天线的多任务学习模型的求解

方向图可重构稀疏阵列天线的多任务学习模型为非凸的优化问题，其可以等价为

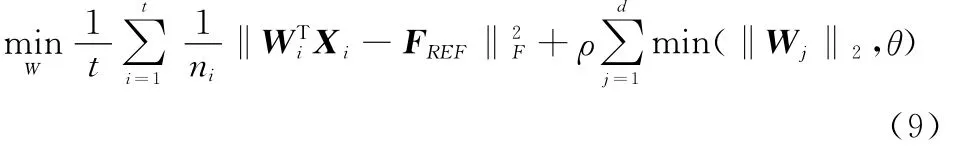
对式（9）的求解可以等价为

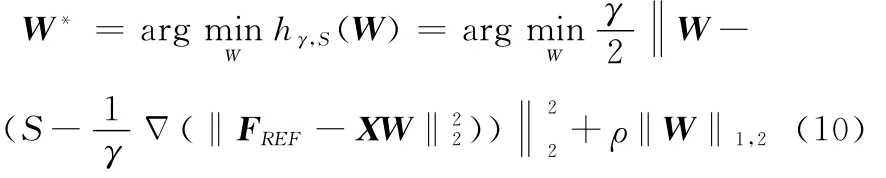
根据迭代收缩阈值的方法，可知

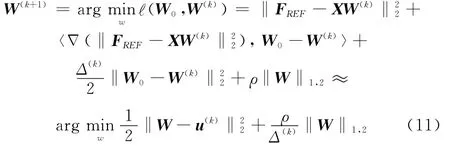
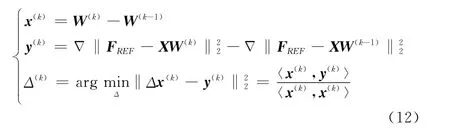
对其进行线搜索

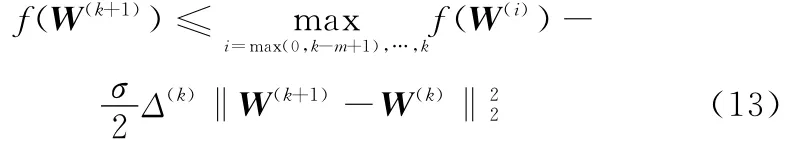
式中，σ∈（0，1）为常数；m＝1表示单调递减；m＞1表示非单调递减。令W0＝［w1，w2，…，wN］为等间距N元阵列天线阵元的激励矩阵。其期望方向图可以通过式（14）得到

式中，δ为一个随机变量，假设它的每一个分量δij都是独立同分布的次高斯随机变量，即存在ζ＞0使得

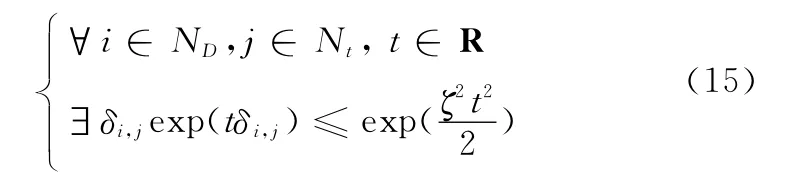
式中，D为方向图的采样点数；t为学习的方向图个数。

假设1给定1≤k≤P，定义

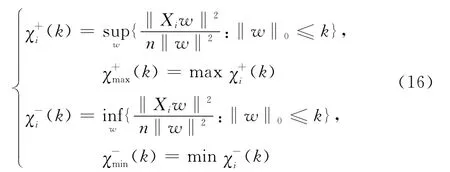
在假设1成立的情况下，定义ξ＝｛（i，j）：wi，j≠0｝。令r为W中非零行的个数，可以假设

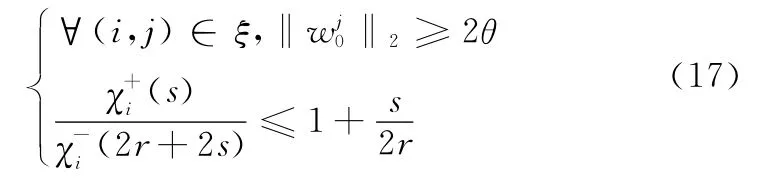
式中，S是一个满足s≥r的整数。如果选择参数ρ和θ，使得对于s≥r，即

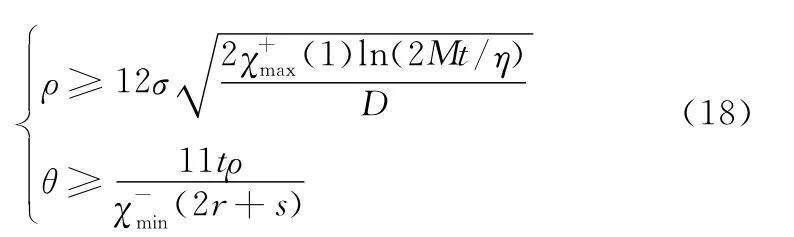
式中，M为阵列天线孔径均分的栅格数。则式（19）参数估计误差的界以不小于1－η的概率成立。

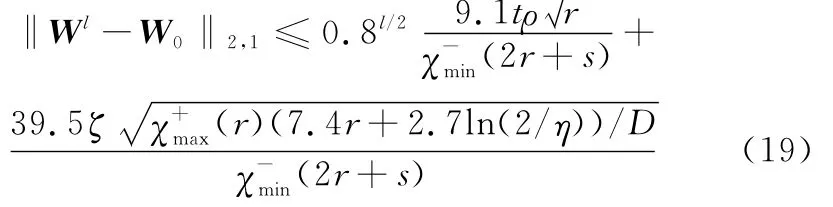
式中，r是W中的非零行数；ρ为方向图综合多任务模型的输入参数，用以控制天线阵列的稀疏；ζ为极小的正数常数；D为方向图总体采样的次数。从式（19）可知，当r确定时，模型输出的精度上界相应确定。

本文算法的具体流程如图3所示。

（1）确定需要重构的方向图个数t以及样本数D，根据要求对需要重构的期望方向图进行采样期望方向图矩阵FREF，根据孔径被均分为M个栅格的N元天线阵列确定直线阵列天线导向矢量矩阵X。

（2）在满足稀疏率的情况下，根据拉格朗日算子与权值矩阵非零个数的关系曲线得到相应的ρ输入。

（3）通过式（18）得到预估的W值，输出稀疏后阵列天线单元的激励值并计算其对应的方向图。

（4）分析输出的稀疏阵列天线重构出来的方向图，对模型的准确性和有效性进行评估。

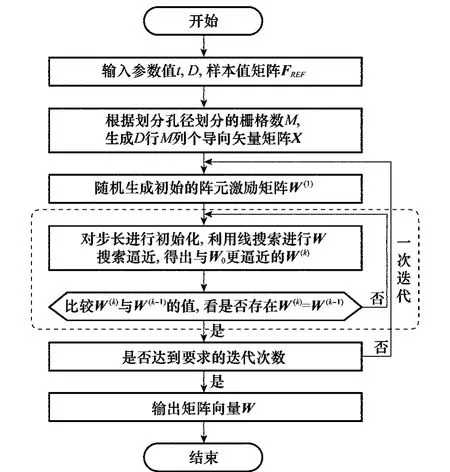
图3 方向图可重构的稀疏阵列天线多任务学习方法流程图

4 实验仿真与分析

4.1 方向图综合的阵列天线稀疏

为了评估多任务学习方法的性能，验证利用多任务学习方法对稀疏线阵进行方向图综合的可行性，文章首先考虑的对象是理想点源构成的20元等间距的切比雪夫阵，阵元的间距为半个波长。切比雪夫阵的旁瓣约束值为－20 dB。以期望方向图和稀疏线阵的方向图的相关度ξ为评估变量。

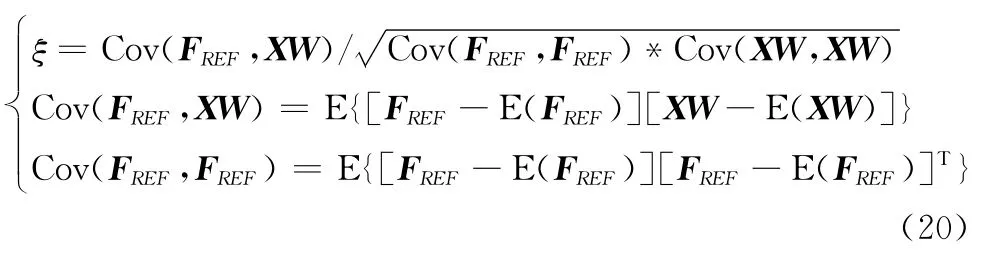
式中，Cov表示两矩阵的协方差阵；ξ∈［－1，1］，1表示最大的正相关，－1表示绝对值最大的负相关。针对稀疏率ζ为20%的线性阵列进行了仿真分析。由于多任务稀疏学习模型是一种不等式约束的优化方法，它具有的显著特点是收缩和选择，即与传统的迭代算法不同，该方法无需每一步都估计所有未知参数，它能收缩待估计的参数的范围，每一步只对少量的入选参数进行估计，而且该模型能自动地选择很少一部分变量进行线性回归，因此，文章设置迭代次数为30次，仿真后的阵元激励位置和阵列方向图如图4所示。从图4中可知，稀疏后的阵列天线方向图与期望方向图拟合程度略有差别，通过计算两者间的相关度，可以得知当ζ＝20%时，切比雪夫均匀线阵的方向图与多任务学习稀疏线阵方向图的相关度为0.902 5，证明利用多任务学习的方法稀疏线阵可以在进行少量迭代计算的情况下实现对单个功能方向图的精确赋形，极大地减小了计算量。

4.2 方向图可重构的稀疏阵列天线设计

为了验证方向图可重构稀疏阵列天线的多任务学习模型的有效性和可行性，文章对阵元数为32，以λ／2等间隔布阵的均匀直线阵列天线进行稀疏及方向图的可重构。对于均匀布阵的直线阵列，通过改变其阵元激励能够重构设计不同的功能方向图，以切比雪夫波束方向图，平顶波束方向图及余割平方波束方向图为例，其相应的各位置单元的激励振幅与方向图如图5所示。

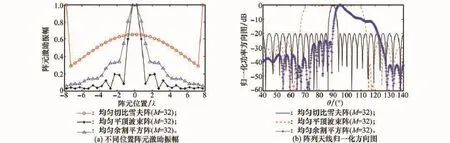
图5 等间隔布阵直线阵列天线单元激励振幅及其相应的方向图

从图5（a）中可知，等间隔布阵的阵列天线的激励是以阵列中点对称分布的。从图5（b）中可以看出，对于平顶波束方向图，其旁瓣峰值电平为－25.91 dB，主瓣宽度为40°。对于余割平方波束方向图，其主瓣宽度为25°，峰值旁瓣电平为－25.05 dB。对于切比雪夫波束方向图，其旁瓣电平为－20 dB，且为常量。对图5（b）中的3类天线方向图进行180点的采样，将采样值作为多任务学习模型响应输入，即矩阵FREF。将32元等间隔布阵的阵列天线孔径划分1 000个栅格点，即D＝1 000，确定模型的特征矩阵输入值X，对其进行稀疏学习，结果如图6所示。

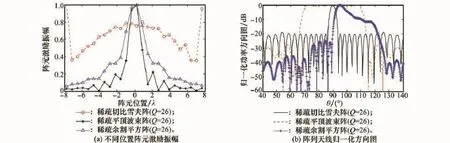
图6 稀疏直线阵列天线单元激励振幅及其相应的方向图

从图6（a）中可知，稀疏后的阵列天线单元数变为26，且阵列是非均匀分布。从图6（b）中可知，尽管稀疏掉一部分阵元，且阵列单元激励分布并不对称，但阵列重构的方向图与等间隔均匀布阵的直线阵列天线方向图极为相似。对平顶波束方向图，其主瓣宽度为40°，峰值旁瓣电平为－27.49 d B。分割平方波束线阵阵元单元激励振幅与相位合作如图7所示。对于余割平方波束方向图，其主瓣宽度为25°，峰值旁瓣电平为－25.12 dB。对于切比雪夫波束方向图，其零点主瓣宽度为8°，旁瓣电平近似为常量，其旁瓣峰值为－19 dB，等间隔均匀阵列和非均匀布阵重构出来的方向图性能参数对比如表1所示，位置及其激励如表2所示。

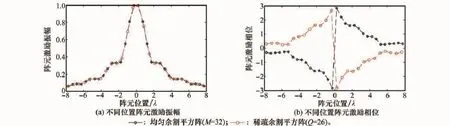
图7 余割平方波束线阵阵元单元激励振幅与相位分布

表1 均匀布阵和稀疏布阵的阵列天线重构出来的天线方向图性能参数对比

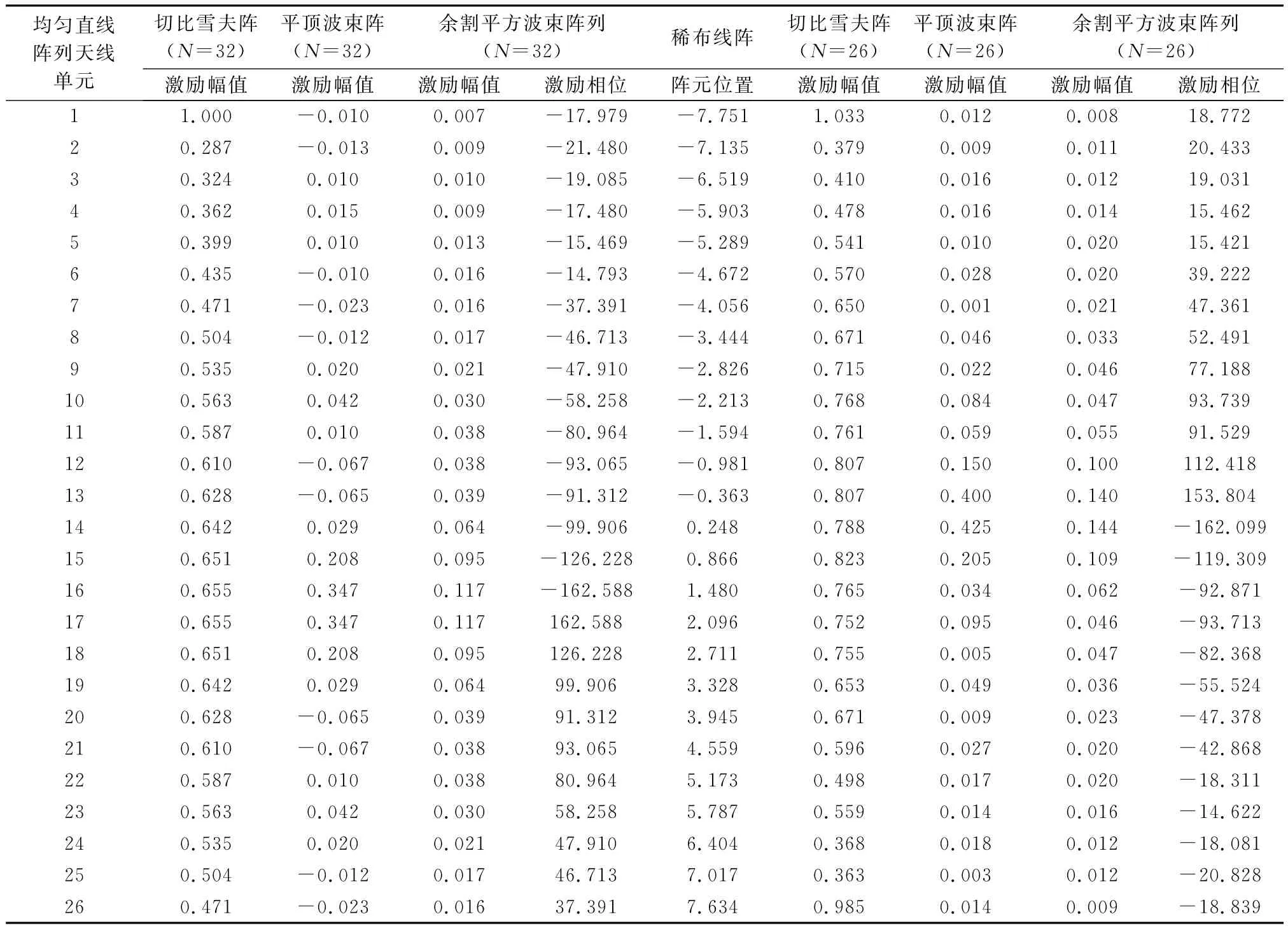
表2 均匀布阵和稀疏布阵的阵列天线单元的位置及其激励

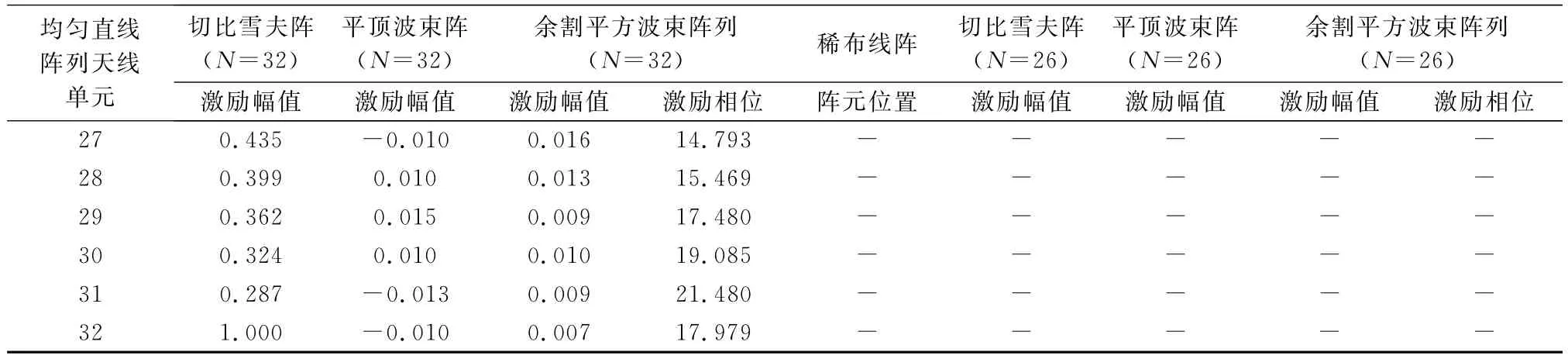
续表2

从表1中的数据可以得出，利用方向图可重构的稀疏阵列天线多任务学习模型对等间隔分布的满阵阵列天线进行稀疏学习，得出的稀疏阵列能用更少的阵元数重构出与均匀布阵的直线阵列天线方向图基本一致的波束方向图。而且，从模型求解数学解析式可知，模型对输入的数据类型没有限制，即模型既能对激励为实数的阵列天线方向图进行稀疏学习，也能对含虚部的复数激励阵列天线方向图进行学习。图7即为余割平方波束方向图等间隔分布阵列天线单元激励与稀疏后的阵列天线单元的激励分布情况，从图7中可以看出，多任务学习能对阵列天线单元激励振幅与相位同时进行稀疏学习优化。

等间隔分布的均匀直线阵列天线和稀疏学习后稀疏布阵的直线阵列天线单元位置及其激励值如表2所示。从表2中可以看出，3类方向图所采用的是同一个结构的稀疏阵列天线，只是各个单元的激励值不同。相对于均匀布阵的直线阵列天线，稀布的方向图可重构阵列天线能够利用更少的阵元数，重构出与均匀布阵天线方向图性能一致的波束方向图，这样不仅能减少方向图可重构阵列天线的设计成本，减轻系统重量和馈电网络的设计复杂度，而且还能进一步减小阵元间的互耦效应，保证阵列天线系统的稳定性。

5 结论

本文利用多任务学习模型，将方向图可重构的稀疏阵列天线设计问题转换成多任务稀疏学习的线性回归问题，建立了基于多任务学习的方向图可重构稀疏阵列设计模型。将模型优化函数转换为最陡梯度下降的优化问题，通过迭代阈值收敛法和分块坐标下降法求解模型的最优函数解。仿真实验表明，利用该方法可以使用更少数目的阵元实现多个天线方向图的联合精确赋形。在满足方向图可重构的同时，使用本文方法还可以减轻系统重量和设计成本，减小了馈电网络的设计复杂度和节省了有限的平台空间，有效抑制单元间的互耦效应。

［1］JosefssonLP.Conformalarrayantennatheoryanddesign［M］.Canada：Wiley-IEEEPress，2006.

［2］AsimAK，AnthonyKB.Nullsteeringinirregularlyspaced sparseantennaarraysusingaperturedistributedsubarraysand hybridoptimizer［J］.IETMicrowaves，Antennas&Propagation，2014，8（2）：86-92.

［3］MahantiGK，DasS，ChakrabortyA.Designofphase-differentiatedreconfigurablearrayantennaswithminimumdynamic rangeratio［J］.IEEEAntennasandWirelessPropagationLetters，2006，14（5）：262-264.

［4］BuccaOM，MazzarellaG，PanarielloG.Reconfigurablearrays byphase-onlycontrol［J］.IEEETrans.onAntennasandPropagation，1991，39（7）：919-925.

［5］GiesD，Rahmat-samiiY.Particleswarmoptimizationforreconfigurablephasedifferentiatedarraydesign［J］.Microwaveand OpticalTechnologyLetters，2003，38（4）：168-175.

［6］SubhashiniKR，PavanKK，LalithaG.Reconfigurablearray antennaswithsidelobelevelcontrolbygeneticmodulation［C］∥Proc.oftheStudents’TechnologySymposium，2011：14-16.

［7］ChengGH，LeiX，ChenZY.Simulationandmodelingofrectangularringreconfigurableantenna［J］.JournalofInformation EngineeringUniversity，2014，15（1）：57-61.（陈国虎，雷雪，陈紫阳.矩形环可重构天线的建模和仿真研究［J］.信息与工程大学学报，2014，15（1）：57-61.）

［8］ZhengRP，ShiZ，QuY.Apatternreconfigurableantennaarraywithfiveprintedmonopoles［J］.JournalofMicrowaves，2013，29（3）：23-27.（郑如萍，施展，瞿颜.五元印刷单极子方向图可重构阵列天线［J］.微波学报，2013，29（3）：23-27.）

［9］ChenGH，CaoK，JiangH.Adaptivereconfigurableantennafor cognitiveradio［J］.ChineseJournalofRadioScience，2013，28（6）：1139-1144.（陈国虎，曹凯，江桦.用于认知无线电的自适应可重构天线研究［J］.电波科学学报，2013，28（6）：1139-1144.）

［10］CaoK，ChenGH，JiangH.Researchandimplementationof geneticalgorithm-basedreconfigurableantennasystems［J］.JournalofInformationEngineeringUniversity，2013，14（5）：557-562.（曹凯，陈国虎，江桦.基于遗传算法的可重构天线系统研究与实现［J］.信息与工程大学学报，2013，14（5）：557-562.）

［11］MahantiGK，ChakrabortyA，DasS.Designoffullydigital controlledreconfigurablearrayantennaswithfixeddynamic rangeratio［J］.JournalofElectromagneticWavesandApplications，2007，21（1）：97-106.

［12］SimeoniM，LagerIE，ComanCI.Implementationofpolarizationagilityinplanarphased-arrayantennasbymeansofinterleavedsubarray［J］.RadioScience，2009，44（2）：127-136.

［13］OliveriG，MassaA.Fullyinterleavedlineararrayswithpredictablesidelobesbasedonalmostdifferencesets［J］.IETRadar，SonarandNavigation，2010，4（5）：649-661.

［14］OliveriG，LizziL，MassaA.ADSinterleavedarrayswithreconfigurable polarization［C］∥Proc.of the IEEE Antennas and Propagation Society International Symposium，2010：1- 4.

［15］Ando R，Zhang T.A framework for learning predictive structures from multiple tasks and unlabeled data［J］.The Journal of Machine Learning Research，2005，6（3）：1817- 1853.

［16］Abernethy J，Bach F，Evgeniou T.A new approach to collaborative filtering：operator estimation with spectral regularization［J］.The Journal of Machine Learning Research，2009，10（4）：803- 826.

［17］Argyriou A，Evgeniou T，Pontil M.Multi-task feature learning［J］.Advances in Neural Information Processing Systems，2007，19（8）：39- 44.

［18］Zhang Y，Yeung D.A convex formulation for learning task relationships in multi-task learning［C］∥Proc.of the 26th Conference on Uncertainty in Artificial Intelligence，2010：733- 742.

［19］Obozinski G，Taskar B，Jordan M.Joint covariate selection and joint subspace selection for multiple classification problems［J］.Statistics and Computing，2010，20（11）：231- 252.

［20］Nesterov Y.Smooth minimization of non-smooth functions［J］.Mathematical Programming，2005，103（4）：127- 152.

［21］Liu C，Peng J Y.Research of classification method for natural images based on multitask learning［J］.Application Research of Computers，2012，29（7）：2773- 2775.（刘成，彭进业.基于多任务学习的自然图像分类研究［J］.计算机应用研究，2012，29（7）：2773- 2775.）

Design of pattern reconfigurable sparse arrays based on multi-task learning

LI Long-jun1，2，WANG Bu-hong1，XIA Chun-he2，SHEN Hai-ou1
（1.School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China；2.School of Computer Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

The pattern reconfigurable antenna array can dynamically alter the array pattern in need and the sparse arrays benefit the array design in expense and complexity.A novel method based on multi-task learning is proposed for the optimal design of pattern reconfigurable sparse array antennas in view of the minimum number of elements and pattern matching as perfect as possible.The design of sparse and reconfigurable antenna array is reformulated as an equivalent problem of multi-matrices linear regression，and the iterative shrinkage threshold method for multi-task learning is exploited to achieve the compromise between the array sparseness and pattern matching.Simulation results demonstrate that multi-pattern reconfigurations can be realized with the sparse layout deduced from the proposed method.

reconfigurable patterns；sparse array antenna；multi-task learning；shaped beam pattern

TN 820

10.3969／j.issn.1001-506X.2015.12.01

李龙军（198-8-- ），男，博士研究生，主要研究方向为阵列天线布阵和阵列信号处理。

E-mail：lilongjunboy＠126.com

王布宏（197-5-- ），男，教授，博士，主要研究方向为信号与信息处理、天线布阵和网络防护。

E-mail：wbhcx＠yahoo.com.cn

夏春和（196-5-- ），男，教授，博士，主要研究方向为网络安全与防护、网络测量。

E-mail：XCH＠buaa.edu.cn

沈海鸥（199-0-- ），女，博士研究生，主要研究方向为阵列天线布阵和阵列信号处理。

E-mail：326519166＠qq.com

1001-506X（2015）12-2669-08