基于光学自准直技术的导航系统姿态输入输出方法

熊成强，钱 江，沈扬清，孙 晨，徐 凯，贾立民，李 莉

（1. 天津航海仪器研究所，天津 300131；2. 海军装备部，北京 100036；3. 北京丹青华瑞科贸有限责任公司，北京 100028）

基于光学自准直技术的导航系统姿态输入输出方法

熊成强1，钱 江2，沈扬清1，孙 晨1，徐 凯1，贾立民1，李 莉3

（1. 天津航海仪器研究所，天津 300131；2. 海军装备部，北京 100036；3. 北京丹青华瑞科贸有限责任公司，北京 100028）

基于光学陀螺的单轴旋转式捷联惯性通常采用角度传感器来实现方位角的输出，但其测量结果受角度传感器自身精度、回转轴系、橡胶减震器及防冲击减震器的影响较大。为提高姿态传递精度，提出一种基于自准直仪和多面镜的光学传递方案，通过光学方法将输出平面与惯组直接建立关系，从而减少中间环节，消除角度传感器误差对系统方位角输出带来的误差，可有效避免传统测量中各种因素的影响。通过模拟试验该方案三个姿态角的传递精度均可达到5″ 以内，满足惯性系统的高精度姿态传递需要。

姿态传递；自准直仪；多面镜；折转光管

近年来，基于光学陀螺的单轴旋转式捷联惯性导航系统应用越来越广泛，单轴旋转式捷联系统可以通过旋转惯组来调制陀螺中有规律漂移和加速度计零位偏差，从而提高系统精度。然而，旋转调制会引起惯组的姿态信息不能直接反映载体的姿态，需要经过姿态转换才能转换为载体姿态。使用传统方法转换过程容易引入误差，进而影响惯导系统的姿态输出精度。

本文提出一种基于光学自准直仪的传递方法，直接将惯组姿态信息与载体姿态信息相关联，减小了旋转捷联系统方位角输出误差，提高了惯导系统姿态输出的精度。

1 传统的单轴旋转捷联系统

旋转式捷联系统是通过转位机构将惯性元件组件（以下简称惯组）进行旋转，处于旋转对称位置的同一惯性元件的零位误差方向相反，当转速足够快时，可认为旋转周期内元件零位变化不大，通过此旋转使该惯性元件的零位误差在对称位置上的累积为零，从而减少了该元件零位误差对捷联系统对准和导航过程的影响。

旋转式惯性系统姿态的输出是通过惯组与载体的相对关系，将惯性元件测得到的惯组与地理系的转换关系转到载体与地理系的转换关系。由于旋转式系统惯组与载体并无直接联接，如何得到惯组与载体的相对关系成为旋转式捷联系统姿态输出的关键。通常，旋转式捷联系统是通过角度传感器来实现方位角的输出。

1.1 组成方式

从单轴旋转式捷联系统旋转调制的作用来看，旋转式捷联系统要求旋转机构能够使惯组旋转在一个相对于载体平稳的平面上，同时能够精确输出旋转体与载体的转位信息。单轴激光陀螺旋转系统如图1所示。

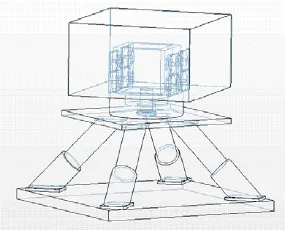
图1 托盘式激光陀螺旋转捷联系统Fig.1 Single-axis rotating INS with a tray

单轴旋转捷联系统中，惯性元件组件通过橡胶减震器固定到旋转体组件之上，旋转体组件通过轴承、电机等器件联接在托盘组件之上，托盘组件及箱体通过防冲击减震器与载体联接。

1.2 旋转式捷联系统方位角输出运算

捷联系统的惯性元件敏感地球自转角速度Ωie和重力加速度g，通过初始对准建立惯组相对地理系的转换矩阵，而系统需要提供的是载体与地理系的转换矩阵，构造惯组围绕旋转的惯性系统坐标系O系，其Z轴与惯组转轴重合指向天向，Y轴为指向车首方向在与Z轴垂直平面上的投影。

1.2.1 惯组系与O系之间的变换矩阵

惯组系绕惯性系统坐标系O系的Z轴旋转，初始时刻惯组Y轴与O系Y轴重合，旋转后某一时刻惯组Y轴与O系Y轴之间的角度可以通过角度传感器测得为η，则有：

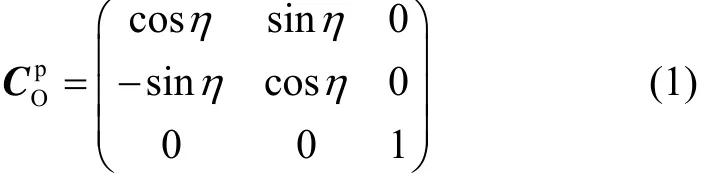
1.2.2 O系与载体系之间的变换矩阵

由于旋转体组件的安装不可能完全垂直于载体平面，必然存在着相对于载体平面的角度，使O系相对载体系有误差角ξzx、ξzy，如图2所示。则有

由以上公式可以得到：

图2 O系与载体系之间的变换Fig.2 Transformation from O-frame to b-frame

1.3 误差分析

此方案能够建立载体系与地理系之间的转换矩阵，从而得到姿态角。但是在实际使用中，该方法得到的姿态角的精度受以下几个方面的影响。

1.3.1 角度传感器器件误差

通过对以上公式的分析，角度传感器的误差是一比一地影响所得的姿态角误差的。目前常用的测角机构有旋转变压器、圆感应同步器、光电码盘、光栅环等。旋转变压器精度较低，圆感应同步器放大电路复杂且安装要求高，光电码盘精度低且可靠性不高，光栅环供应受限且价格过高。因此以上器件均不能满足批产的高精度惯性系统。

1.3.2 轴系加工及装配误差

轴承的装配过程和轴系结构件的加工过程对工艺水平的要求很高。由加工及装配产生的轴系的回转锥角将造成角度测量的误差。

1.3.3 轴系旋转的不稳定性

惯性系统旋转时，由于惯组较重且重心与轴系中心存在不同轴偏差，导致当惯组旋转时，惯性系统会在一定范围内进行有规律的抖动和无规律的章动，而这种转轴的运动难以建立数学模型且即便通过补偿也难以补偿干净，这会带来一定的姿态输出误差。

1.3.4 橡胶减震器变形的不确定性

惯组的姿态输出是惯组相对于地理系的转换关系。在使用二频机抖激光陀螺时，惯性系统的惯组都通过橡胶减震器与旋转体相连接。由于橡胶减震器是活动部件，在不同的受力情况下会产生变形，因此惯组的姿态不能等同于托盘旋转体的姿态，进而与托盘旋转体相固联的角度传感器的输出不能直接反映惯组系与O系的角度关系。又由于减震器变形难以描述，这个误差很难通过数字补偿。因而橡胶减震器的变形会造成惯组坐标轴与旋转体坐标系之间的不确定，引入误差。

1.3.5 防冲击减震器对姿态的影响

系统是通过防冲击减震器与载体联接的。防冲击减震器的特点是冲击小，无变形，也就是说在平常状态下，减震器中的阻尼器等器件并无明显形变。但是由于减震器中除了阻尼器外还有些活动部件，这些部件有一定的自由行程，在载体运动时会随系统重心的变化有一定的活动，造成惯性组件与载体所处平面不平行，继而造成一定的姿态输出误差。

1.3.6 外力扭转和应力释放

角度传感器的定子部分是与转轴固定组件相连接的。由于长时间颠簸和应力释放会造成系统转轴固定组件有一定的变形，这种变形会导致测角机构的电气零位有一定的变化，从而导致系统姿态角输出零位的变化。这种变化会造成系统方位角输出的误差。

综上所述，使用角度传感器的方位角传递方案受到诸多因素的影响，在需要高精度方位角及水平姿态输出的情况下，这种方案是不能满足需求的。

2 光学传递方案

针对角度传感器的方位角输出方案的诸多误差，本文提出一种通过光学方法将输出平面与惯组直接建立关系的实施方案，从而减少中间环节，消除角度传感器误差对系统方位角输出带来的误差。

光学传递方案组成如图3。

本方案中使用两组自准直仪相互垂直安装在与载体固联的底板之上，与惯组相连接的部位安装一多面镜，在与各个自准直仪相对应的位置安装折转光管。

惯性系统工作时，自准直仪发出一束平行光，经由折转光管，投向与惯组固联的多面镜。惯组开始旋转以后，当多面镜中任一面镜的法线旋转至折转光管工作范围内时，反射光线经该面镜的反射进入折转光管，经折转光管回到自准直仪，并在自准直仪CCD平面留下一投影。通过在CCD投影的光斑的位置，可以将此时反射镜面法线与自准直仪光轴建立相对关系。同时第二组自准直仪在与第一组自准直仪接近垂直的位置照射与多面镜的另一个平面，可以得到另一组自准直仪与镜面的相对关系。处于反射位置的镜面与惯组的相对关系已知，且两组自准直仪与载体固联，因此，两组自准直仪的方位向量就可以反映底板坐标系与地理系的转换矩阵，从而将此时的惯组惯性解算得到的惯组相对地理系的相对关系传递给载体，即建立载体与地理系相对关系。继续旋转以后，多面镜离开折转光管的输入范围，此时输出姿态可以通过传统方案进行。当多面镜下一组镜面进入折转光管输入范围时，进行下一次姿态输出。

图3 光学传递方案Fig.3 INS with optical attitude transformation

2.1 光学传递方案的优势

相对传统的角度传感器测角方案本方案有如下优势：

① 传统方案中，转轴的不稳定会带来惯组围绕转轴做近似于锥摆的运动，使得惯组坐标轴及多面镜法线在垂直面上做波浪运动，致使惯组的两个水平姿态角与载体系水平姿态角都有差值。光学方案中，惯组姿态与载体姿态之间的转换关系即两者间的转角通过自准直仪精确求得，从而补偿了这两个角度影响，此项误差不会对输出产生影响。

② 光学方案中，多面镜是与惯组固联，并与惯组一起安装在减震器内，因此多面镜的姿态能够真实代表惯组的姿态，不受橡胶减震器变形的影响。另外两个自准直仪采集两个镜面的角度，只要两个镜面都进入折转光管的输入范围，防冲击减震器变形不会对方位角输出产生影响。

③ 多面镜与惯组固联，多面镜的每个镜面都可以直接的和惯组坐标系建立关系，而解算中实际用到的是镜面法线在惯组坐标系投影与惯组坐标轴之间的夹角，这与多面镜是否在旋转轴中心以及多面镜的安装平面与旋转平面是否平行没有关系，因此多面镜中心是否在惯组旋转中心不影响传递精度。

④ 通过两组自准直仪的测量可以得到惯组的方位、俯仰及横滚三组姿态信息，提高了测量效率。

⑤ 当系统在安装过程中或安装后受到外力或应力释放的影响时，只要折转光管上下两镜面相对关系未变化，对整个姿态传递方案的精度不影响。

2.2 光学对准方案中使用到的光学器件

2.2.1 多面镜

多面镜又称反射多面棱镜，是将360°圆周角按工作面数进行等分，且工作面全部是由外反射平面构成的玻璃或金属直棱柱体。根据圆周的等分数，目前常用的有六、八、九、十二等面体。

本方案中使用的是八面镜，如图4所示。这样一是可以保证两两镜面相互垂直，从而保证两组自准直仪同时进入输入范围，二是可以保证有足够的输出频率。如果需要姿态输出频率较高，可以选择镜面更多的多面镜。

图4 八面镜Fig.4 The polygon mirror

2.2.2 自准直仪

光学自准直仪是根据自准直原理，测量物体微小角度变化的仪器。本方案中使用的是CCD式数字式自准直仪可以由CCD的读数得知目标反射面法线与自准直仪光轴的夹角。

光学自准直仪原理如图5，物镜组焦距为f，在其焦点位置有一光源O，来自光源O的光线经过物镜组折射成为平行光，照射在目标平面镜之后反射回CCD平面成像O′。如果平面镜法线与光管轴存在一个角度θ，根据光的反射性质，反射光线将与入射光线成角2θ，反射形成的像O′ 将与其光源O有一定距离d。高分辨率的CCD可以测量得到d，并由下式得到夹角θ：

图5 光学自准直仪工作原理Fig.5 Operational principle of autocollimator

实际使用时，光源经过分划板形成一十字光束，经反射后返回光管并在CCD上汇聚为一十字光斑（如图6），并可得到十字光斑中心点在CCD平面上的坐标(dx, dy)。

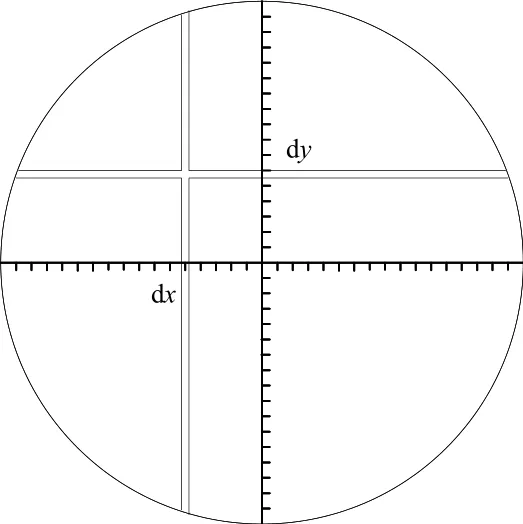
图6 光学自准直仪输出示意图Fig.6 Output window of autocollimator

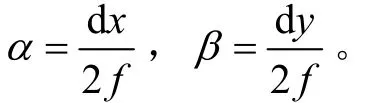
2.2.3 折转光管

折转光管是用壳体把两块平行或垂直的平面反光镜联成一体，以实现出射光和入射光平行，但平移了一段等于折转光管中心长度的距离。本方案采用的折转光管两平面镜的角度为90°，折转光管为垂直架设。

当入射光与下镜面的法线成45°时，按反射定律，出射光和上镜面法线的夹角成45°，出射光与入射光平行，但平移了一段等于折转光管中心长度的距离。如果入射光增大了α角，即入射角为45°+α时，出射光为45°-α，即入射光与出射光保持平行。

当入射光不在法平面内时，入射光与法平面成α角，出射光与法平面成 -α角，入射光与出射光成2α角，这说明折转光管在与法平面垂直的方向上具有2倍敏感性。

图7 折转光管原理图Fig.7 Operational principle of reflex light tube

2.3 姿态输出算法

姿态输出即将惯组得到的与地理系之间的相对关系传递到系统安装平面即与载体固联的部分之上，也就是求得系统安装平面与地理系之间的转换关系，本方案的算法有以下步骤：

① 惯组向输出镜面的传递

系统工作时，当多面镜中的一组镜面进入折转光管的工作范围时，惯组此时的姿态转换矩阵为。由于多面镜与惯组固联，每个镜面都能通过标定建立与惯组之间的关系，即建立镜面法线在惯组系的方位向量，此时在折转光管工作范围的镜面的方位向量为和。可以得到此时这组镜面法线在地理系上

的方位向量：

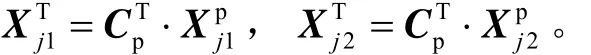
② 输出镜面向自准直仪的传递

自准直仪与载体系固联，自准直仪光轴在载体系的方位向量可以通过标定得到，即和。根据自准直仪和折转光管的工作原理可知，此时自准直仪的输出角度是多面镜输出镜面组法线与自准直仪光轴在与自准直仪固联的载体系上的夹角，即、，由此可以得到输出镜面组法线在载体系上的方位向量：

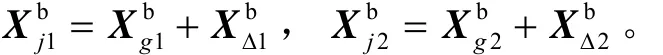
③ 自准直仪向安装平面的传递

由以上步骤可以得到两个镜面在地理系和载体系的方位向量。

2.4 传递范围

本方案中，需要与惯组相固联的多面镜进入折转光管和自准直仪的输入范围才能进行姿态传递，而多面镜是随着惯组进行旋转的。在旋转过程中，由于轴摆等因素其部分镜面都可能超出了折转光管和自准直仪的输入范围，需要分析折转光管和自准直仪的工作范围。

2.4.1 自准直仪工作范围

自准直仪的工作范围是由自准直仪CCD进行精确测量所需要的进光量所决定的。自准直仪所发出的平行光经过一系列光路传播回到自准直仪时，CCD需要一定大小的光斑才能成像和进行测量。这与自准直仪的口径和CCD成像质量相关，本文采用输入范围为1°的自准直仪。

2.4.2 折转光管工作范围

自准直仪发出的平行光经由折转光管照射到多面镜之上，反射后再经由折转光管回到自准直仪的镜头范围。

通过对折转光管的原理分析，经由折转光管返回自准直仪的平行光斑面积与以下因素相关：

① 多面镜法线角度；

② 自准直仪到多面镜的光程长度；

③ 折转光管的通光口径；

④ 折转光管的安装角度。

综上，通过以上分析表明，通过增大自准直仪镜头或折转光管通光面积，减小折转光管光程长度等手段，可以使本方案的姿态输入范围满足旋转系统动态输出的要求。

3 试验验证

为了验证该光学方案姿态传递的精度，进行了如下验证实验。

3.1 试验方案

在一双轴转台中心（接近即可）固定一个正八面镜，并在八面镜之上固定一个正六面体。架设六面体是模拟惯组，通过测量六面体的姿态来得到惯组姿态。在转台附近树立一经纬仪作为此次试验的北向基准。

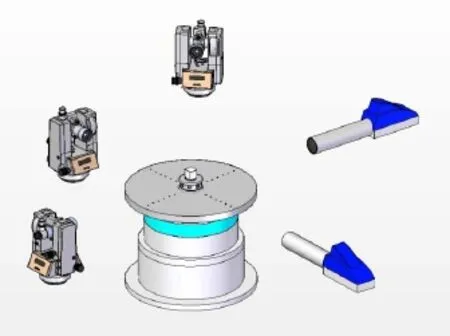
图8 试验方案示意图Fig.8 Experiment scheme

3.2 试验步骤

首先需要标定八面镜各面法线与惯组之间的相对关系。固定好八面镜与六面体之后，使用高精度经纬仪测量八面镜各个镜面，得到各镜面法线在地理系中的方位向量，同时测量六面体中作为首向和东向的两个镜面法线，建立六面体惯组系与地理系的姿态矩阵，通过运算可以得到八面体个镜面在六面体惯组系中的方位向量。

进行测量时，架设两个高精度自准直仪，瞄准互为垂直的两个八面镜镜面；转动转台方位轴45°，使下一组镜面进入自准直仪测量范围，并测量此时这组镜面的角度，用一经纬仪测量此时六面体的姿态；转台转至下一位置，进行测量直至八组镜面全部测完。改变转台角度，重新调整自准直仪重复以上步骤进行下一组试验。

3.3 试验数据

通过以上试验得到的数据运算后得到两自准直仪固联的载体系的姿态角。表1列出了部分运算结果。

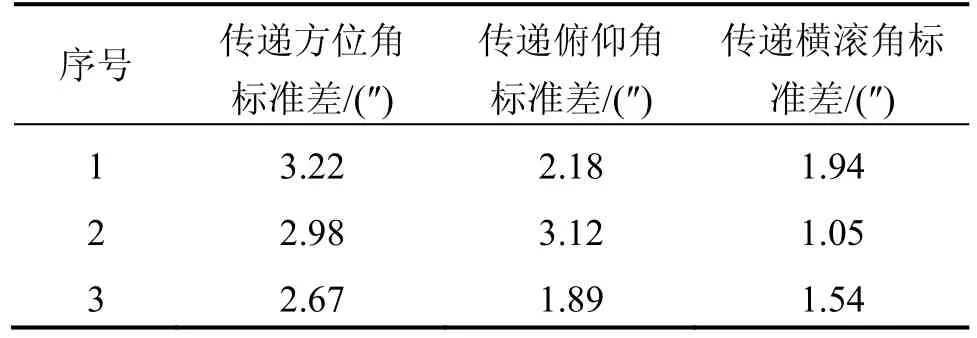
表1 验证方案试验结果Tab.1 Test results of attitude transformation

4 结 论

本文提出一种单轴旋转式捷联惯性导航系统的光学姿态测量方法。根据坐标系间矩阵转换关系，得到一种单轴旋转式捷联惯性导航系统高精度姿态测量方法。原理分析和试验验证表明，与传统姿态输出方案相比，本文所提出的光学对准旋转式系统姿态输出方案具有操作环节少、输出精度高、可靠性强的特点，能够满足高精度姿态输出的需要。

（References）：

[1] 仲岩, 王丹丹. 一种高精度捷联惯组方位引出方法[J]. 中国惯性技术学报, 2014, 22(6): 845-848. Zhong Yan, Wang Dan-dan. Azimuth extraction method for high precision strapdown IMU[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 845-848.

[2] 牛立, 赵慧. 战车用惯性定位定向系统的支架误差分析与补偿[J]. 中国惯性技术学报, 2007, 15(5): 522-525. Niu Li, Zhao Hui. Analysis and compensation of the bracket error for inertial positioning and heading system [J]. Journal of Chinese Inertial Technology, 2007, 15(5): 522-525.

[3] 胡佩达, 高钟毓, 张嵘, 等. 基于三轴摇摆台的高精度姿态试验系统[J]. 中国惯性技术学报, 2013, 21(2): 271-274. Hu Pei-da, Gao Zhong-yu, Zhang Rong, et al. High accuracy attitude testing system based on three-axis test table[J]. Journal of Chinese Inertial Technology, 2013, 21(2): 271-274.

[4] Zhang L, Wang A G. Vessel surface equipment attitude measurement based on conventional inertial reference system[J]. Advanced Materials Research, 2012, 629: 878-883.

[5] Johnson G, Waid J, Primm M, et al. Ship attitude accuracy trade study for aircraft approach and landing operations [C]//IEEE Position Location and Navigation Symposium. 2012: 783-790.

[6] Gu D Q, El-Sheimy N, Hassan T, et al. Coarse alignment for marine SINS using gravity in the inertial frame as a reference[C]//IEEE Position, Location and Navigation Symposium. 2008: 961-965.

[7] Yu Q, Jiang G, Fu S, et al. Fold-ray video metrics method for the deformation measurement of pointer visible large structures[J]. Applied Optics, 2009, 48(24): 4683-4687.

[8] Johnson G, Waid J, Primm M, et al. Ship attitude accuracy trade study for aircraft approach and landing operations[C]//IEEE Position, Location and Navigation symposium. 2012: 783-790.

[9] Zhang L, Wang A G. Vessel surface equipment attitude measurement based on conventional intertidal reference system[J]. Advanced Materials Research, 2012, 629: 878-883.

Input/output method for INS attitude by optical autocollimation

XIONG Cheng-qiang1, QIAN Jiang, SHEN Yang-qing1, SUN Chen1, XU Kai1, JIA Li-min1, LI Li3
(1. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China; 2. Equipment Department of the Navy, Beijing 100036, China; 3. Dantsin Huarui Technology Limited Company, Beijing 100028, China)

In single-axis rotating INS with optical gyros, an angle sensor is usually used to realize the attitude’s output. But the accuracy of this method is significantly influenced by angle sensor, rotary shaft, rubber absorber, and anti-shock absorber. To solve this problem, an attitude transferring scheme by using autocollimators and polygon mirrors is proposed. The relationship between output plane and IMU is directly established by an optical method, thereby reducing the intermediate steps and effectively avoiding the above influencing factors in traditional method. The simulation results show that the transfer accuracies of the three attitudes are all within 5″, which satisfies the need of attitude transfer in high precision INS.

attitude transfer; autocollimator; polygon mirror; reflex tube

U666.1

A

1005-6734(2015)02-0275-06

10.13695/j.cnki.12-1222/o3.2015.02.024

2014-12-10；

2015-03-30

国防科技预研重点项目（A0320132002）

熊成强（1965—），男，高级工程师，从事惯性系统的研究。E-mail：Xiongcq01@163.com