基于熵值法赋权灰色关联决策的地形辅助导航适配区选择

徐晓苏，汤郡郡，张 涛，岳增阳

（1. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

基于熵值法赋权灰色关联决策的地形辅助导航适配区选择

徐晓苏1,2，汤郡郡1,2，张 涛1,2，岳增阳1,2

（1. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

传统地形辅助导航适配区选择主要根据某一个地形特征参数的大小决定，因此不可避免地存在对地形适配性评判的不全面性。为了克服传统方法的缺点，提出了一种基于熵值法赋权灰色关联决策的地形辅助导航适配区选择方法，该方法综合考虑了地形标准差、粗糙度、地形高度熵及相关系数对适配区选择的影响。首先，利用计算得到的各特征参数值构建灰色决策矩阵；其次，对决策矩阵进行极差变换以及归一化处理得到灰色关联判断矩阵；最后，采用熵值赋权法客观计算各决策属性的权重，得到地形适配性综合评价指标。仿真结果表明，在评价值高的区域进行地形辅助导航，其匹配误差将更小。

地形辅助导航；地形信息量；适配区；熵值法赋权；灰色关联决策

惯性导航因为同时具有自主性、隐蔽性和能获取载体完备运动信息的独特优点，成为了水下潜器实现高精度导航定位的主要方法。但是，惯性导航系统最大的缺点就是其系统误差随时间积累。而地形辅助导航具有自主、连续、全天候工作、导航定位误差不随时间积累等优点，能够提供外界位置信息来修正主惯性导航系统的误差，是水下潜器理想的辅助导航定位手段。

地形辅助导航系统的定位精度不仅与匹配算法有关，而且与地形匹配区域的选择有关。衡量地形信息量的主要特征参数包括地形标准差、地形相关系数、地形粗糙度和地形熵等，它们分别反映了水下地形高程值的离散程度、集中趋势、光滑程度等地形固有属性，对于研究地形特征与匹配定位精度的关系具有十分重要的意义。

传统地形匹配区域的选择主要根据某一个单一特征参数的大小决定，不可避免地存在对地形区域适配性评判的不全面性。因此提出将熵值法赋权灰色关联决策应用于水下地形辅助导航适配区的选择，综合考虑各参数对地形匹配区域的影响得到适配性评价指标，并且通过仿真验证了该评价指标的合理性和有效性。

1 地形导航信息量参数

海底地形数据一般采用格网矩阵的方式存储，设某地形的经纬度为m×n网格，网格点坐标为(i,j)处的地形高程值为h(i,j)，地形信息量的主要特征参数包括地形标准差、地形相关系数、地形粗糙度和地形高度熵等，它们的具体定义如下：

① 地形标准差

地形标准差反映的是地形高程偏离地形平均高程的范围，是反映地形整体起伏剧烈程度的宏观参数。地形标准差σ定义为：

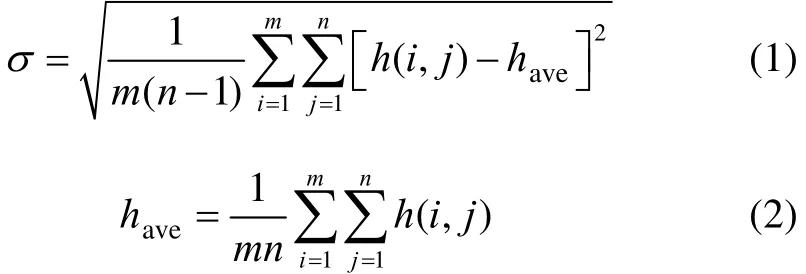
式中，have为地形高度平均值。

② 地形相关系数

地形相关系数是反映地形相关性的特征参量，相关系数R定义为：

式中，Rlong表示经度方向相关系数，反映了经度方向的地形剖面在纬度方向上的相关程度；Rlati表示纬度方向相关系数，反映了纬度方向的地形剖面在经度方向的相关程度。

③ 地形粗糙度

地形粗糙度反映了地形的光滑程度，是刻画地形局部起伏大小的特征参量。地形粗糙度r定义为：

式中，rlong表示经度方向的粗糙度，rlati表示纬度方向的粗糙度。

④ 地形高度熵

地形高度熵是反映地形所含信息量大小的特征参量。地形高度变化越明显，则地形高度熵越小。地形高度熵Hf定义为：

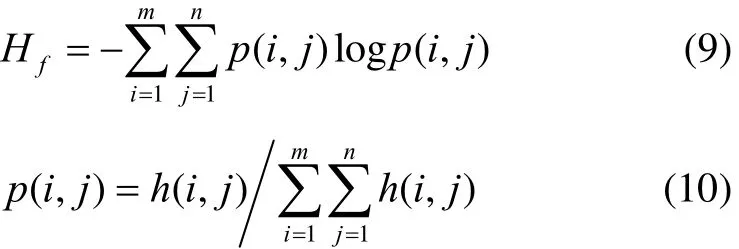
式中，p(i,j)表示归一化高程值。

2 基于熵值法赋权灰色关联决策的地形辅助导航适配区选择准则

由文献[3]可以知道，不同的特征参数对地形信息量丰富程度以及地形适配性的影响不同。在条件一定的情况下，地形高度熵、地形相关系数越小，地形信息量越丰富，该区域适配可能性越大；地形标准差，地形粗糙度越大，地形信息量越丰富，适配可能性越大。为此，需要综合考虑各参数对适配性的影响，采取多特征融合的方法，将不同的特征参数融合成一个特征向量T=(σ,r,Hf,R)，并根据该特征向量进行导航区域适配性综合研究，得到一种更为全面的地形匹配适配区选择方法。

2.1 决策矩阵的构造

设航行区域中有m个决策方案（地形候选区域）X1,X2,…,Xm，每个决策方案有n个评价指标（特征参数）G1,G2,…,Gn，方案Xi(i=1,2,…,m)在目标Gj(j=1,2,…,n)下的属性值为xij，则决策矩阵为：

2.2 求解规范化矩阵

已知地形适配能力随相关系数、高度熵的减小而增大，随地形标准差、粗糙度的增大而增大，因此可以把地形相关系数和高度熵看作是成本型指标，把地形标准差和粗糙度看作是效益型指标，对决策矩阵X进行极差变换得到规范化矩阵Y=(yij)m×n，其中，

2.3 灰色关联判断矩阵的构造

序列，以第i方案属性值yi(j)={yij|j=1,2,…,n}(其中，i=1,2,…,m)作为比较序列，则yi与y0在第j项指标下的关联系数计算公式为：

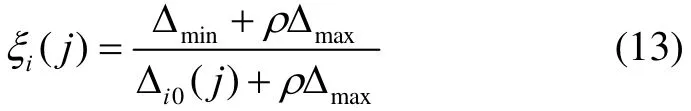
灰色关联判断矩阵如下：

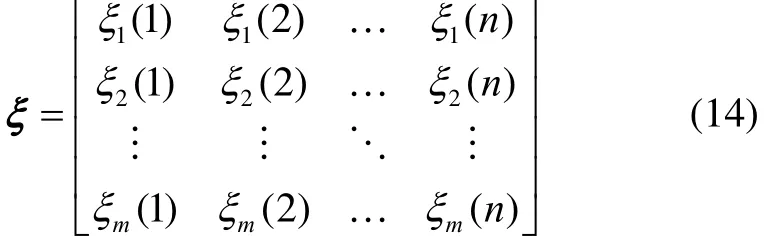
2.4 熵值法计算权重

① 由于求熵值时要用对数进行计算，为了避免对数无意义，可以将规范化矩阵中的数据进行平移，则第i个方案对第j个指标属性的贡献度fij可以定义为：

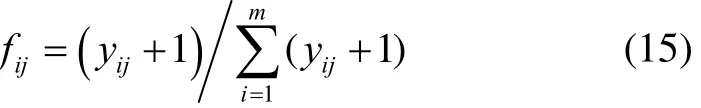
② 对于此贡献度所包含的信息内容，可以用熵Ej来表示所有方案对第j个指标的贡献总量：

③ 定义第j个指标下各方案贡献度的差异系数gj，并根据差异系数求得指标权重wj：

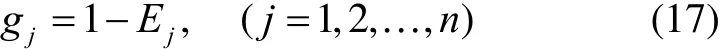
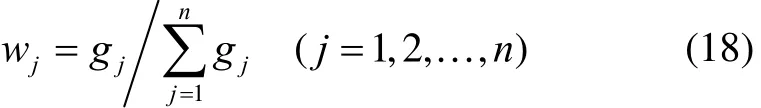
2.5 求解灰色关联度综合评价值

方案Xi的灰色关联度综合评价值为：

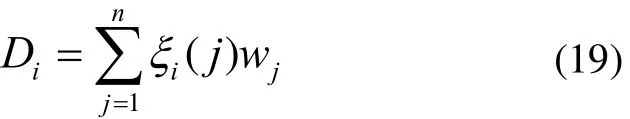
对m个决策方案的多属性决策实质上就是对这些方案的灰色关联度综合评价值进行排序比较。评价值Di越大，所对应的决策方案越好，也即对应候选区域的可导航能力越高。

3 仿真分析

3.1 有效性验证

为便于对比和分析，以某海域水深数据为例来确定导航适配区选择准则，其地形高程三维图如图1所示。

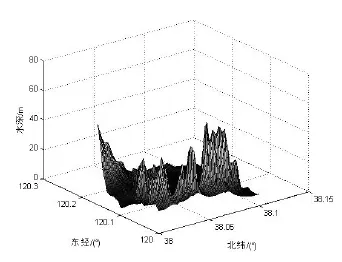
图1 三维地形图Fig.1 3D terrain

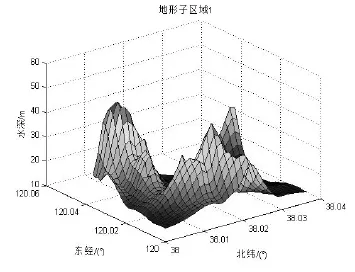
图2(a) 地形1Fig.2(a) Terrain 1

在图中选取4块网格（网格间距0.001 25°，也即139 m）大小一致的地形候选子区域作为待评方案，其中子区域1的起点为（北纬38°，东经120°），子区域2的起点为（北纬38.075°，东经120°），子区域3的起点为（北纬38.1125°，东经120°），子区域4的起点为（北纬38°，东经120.0375°），它们的地形三维图如图2所示。

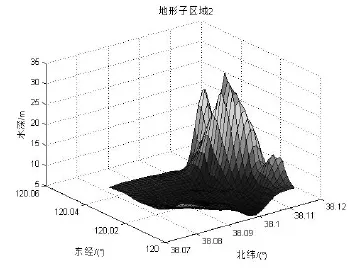
图2(b) 地形2Fig.2(b) Terrain 2

图2(c) 地形3Fig.2(c) Terrain 3

图2(d) 地形4Fig.2(d) Terrain 4

分别计算上述子地形区域的标准差、粗糙度、相关系数和地形高程熵，各参数值如表1。

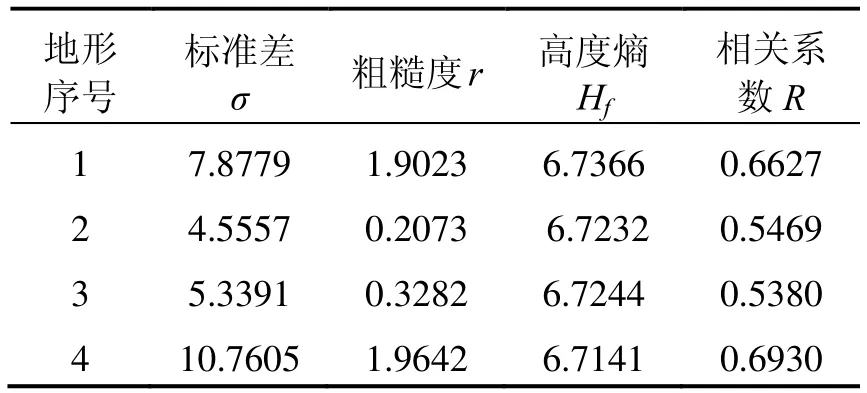
表1 4块子区域地形信息量Tab.1 Terrain information of four sub-areas

① 构造决策矩阵

② 计算规范化矩阵

③ 计算灰色关联度矩阵

④ 计算贡献度矩阵

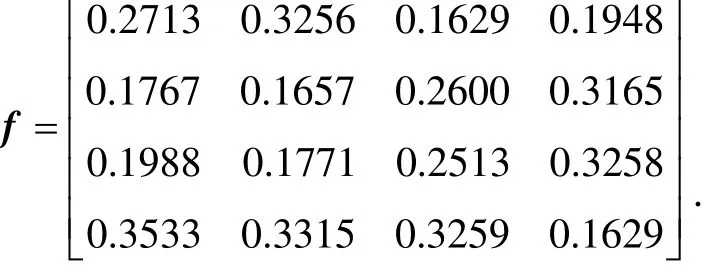
⑤ 由此可以得到各指标权重向量W= (0.2362, 0.3183, 0.1768, 0.2686)，根据式(18)得到四个方案的综合评价值为D=(0.5817, 0.5236, 0.5581, 0.8209)，即四块地形适配能力排序为：地形4>地形1>地形3>地形2。

在上述子地形区域中，采用基于等值线的最近点迭代(ICCP)算法进行地形匹配仿真，仿真结果如图3所示。图3中，1#为理想轨迹，2#为主惯性导航系统指示轨迹，3#为ICCP匹配轨迹。比较图3(a)、3(b)、3(c)、3(d)可以发现，地形子区域4的匹配效果明显较好，相反，地形子区域2的匹配效果明显较差。分别计算四块子区域ICCP匹配结果的均方根误差来定量比较各区域匹配结果的优劣性，计算结果如表2。

表2 4块子区域匹配结果Tab.2 Matching results of four sub-areas

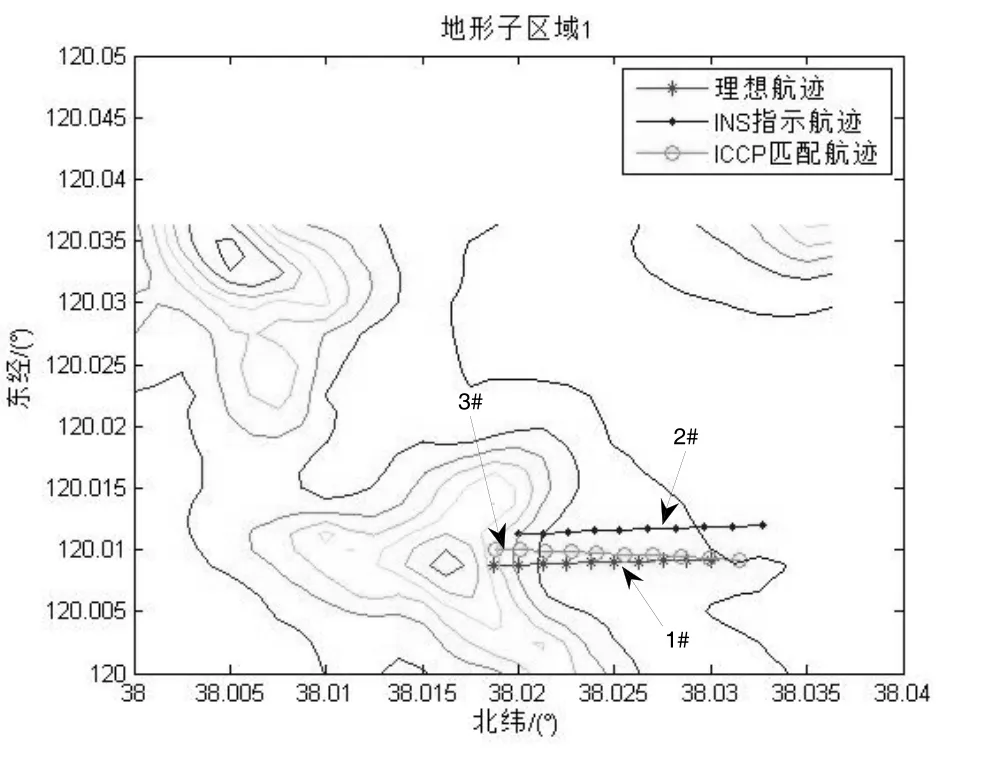
图3(a) 地形1匹配结果Fig.3(a) Matching result of terrain 1

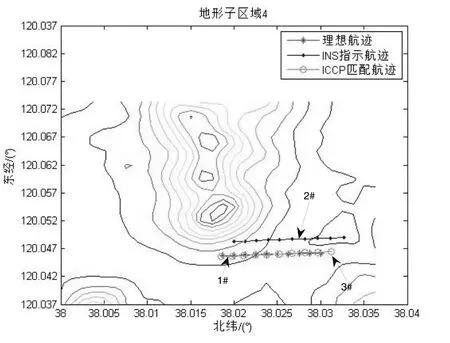
图3(d) 地形4匹配结果Fig.3(d) Matching result of terrain 4

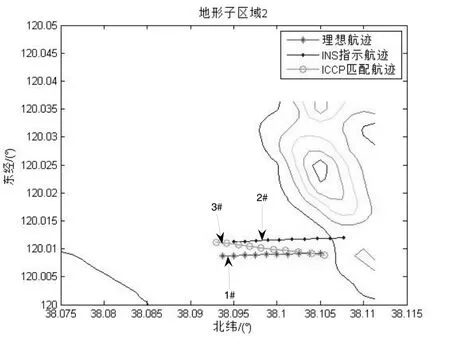
图3(b) 地形2匹配结果Fig.3(b) Matching result of terrain 2

从表2中可以看出，地形的选择对ICCP算法有很大影响，依据熵值赋权灰色决策得出的综合评价值越大的地形子区域，其匹配均方根误差值（RESM）越小，也即适配能力越佳。

另外，根据不同的地形特征量对四块地形的适配能力进行排序，并与本文提出的方法进行比较，其结果如表3所示。

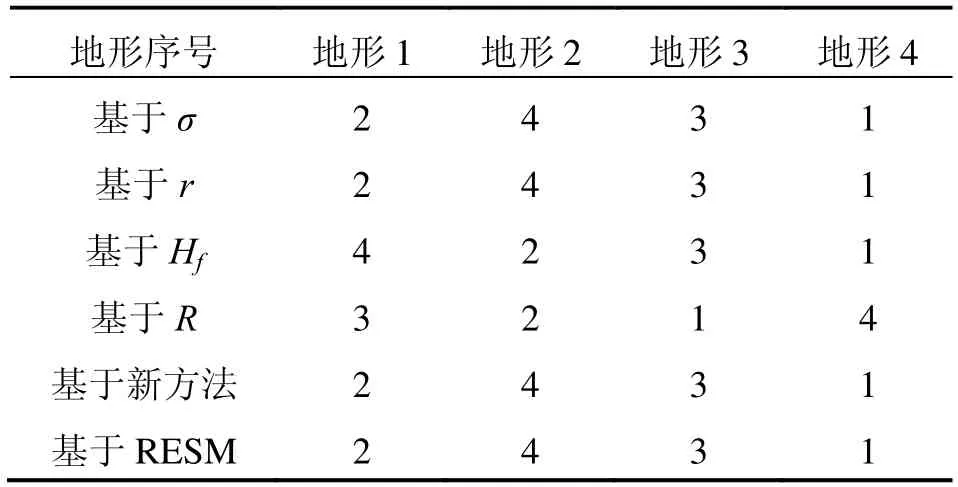
表3 不同参数排序结果Tab.3 Rank results according to different parameter

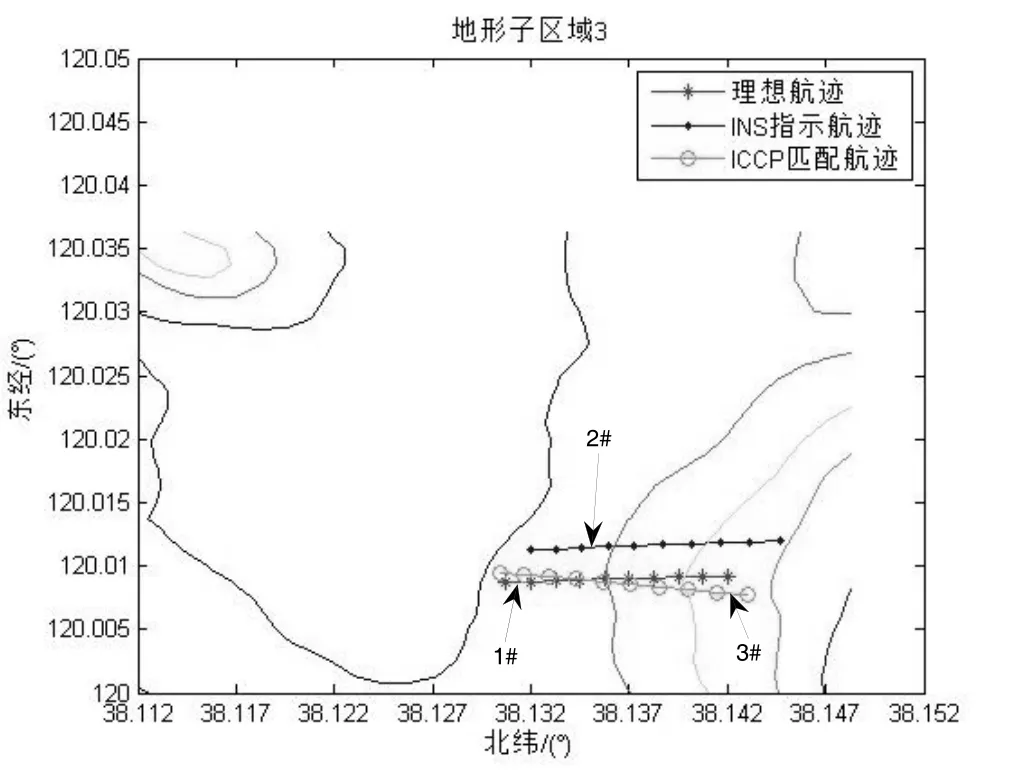
图3(c) 地形3匹配结果Fig.3(c) Matching result of terrain 3

从表3可以看出，根据单一地形特征量得到的适配能力排名具有较大差异，与实际匹配结果也存在较大差异，而提出的方法得到的适配能力排名与实际匹配结果是一致的。

3.2 多地形验证

选取10块不同的地形，分别计算10块子地形区域的标准差、粗糙度、相关系数和地形高程熵，并按照本文描述的方法计算各地形的适配能力排名，其结果如表4。从表4中可以看出，综合评价值排名与RESM值排名几乎一致，只有地形4和地形6出现不一致情况，这是由于这两块地形较为相似，地形变化相当平缓，地形高度变化在20 m以内，具体地形如图4和图5所示。

实际应用中，可以根据均方根误差与航行器定位要求精度之间的关系确定某一地形是否适合进行地形辅助导航。假设要求航行器定位精度小于1个网格，即139 m，则上述10块地形区域中，均方根误差小于139 m的地形可被认为是地形适配区域。

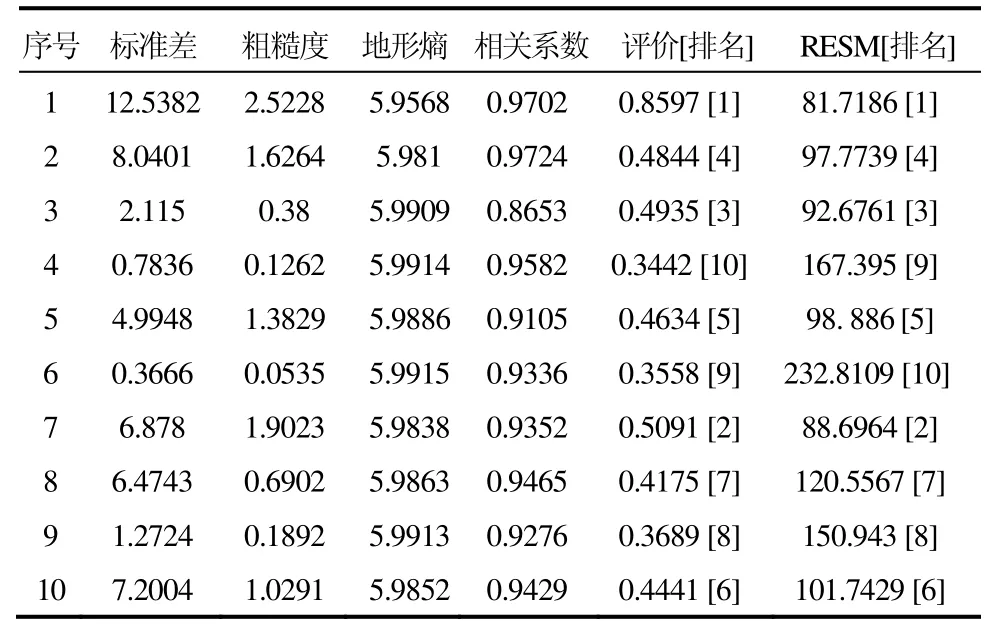
表4 仿真结果Tab.4 Simulation results

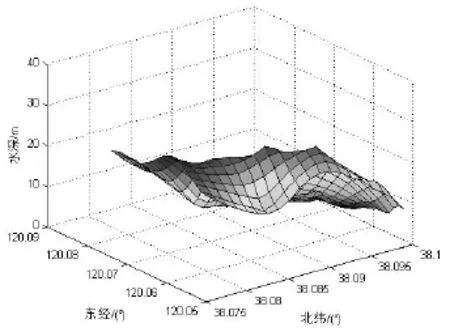
图4 地形4Fig.4 Terrain 4

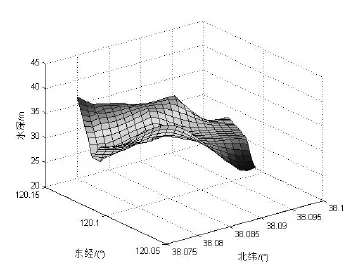
图5 地形6Fig.5 Terrain 6

4 结束语

地形辅助导航系统的定位精度对地形的选择有很大影响。采用基于熵值赋权的灰色关联决策算法来综合评价地形的适配能力，克服了只靠单一特征参数评价的不全面性问题，可以作为匹配区域选择、地形适配性分析以及航迹规划的数量性依据。

（References）：

[1] 徐晓苏, 吴剑飞, 徐胜保, 等. 基于仿射修正技术的水下地形ICCP匹配算法[J]. 中国惯性技术学报, 2014, 22(3): 362-367. Xu Xiao-su, Wu Jian-fei, Xu Sheng-bao, et al. ICCP algorithm for underwater terrain matching navigation based on affine correction [J]. Journal of Chinese Inertial Technology, 2014, 22(3): 362-367.

[2] 宋捷. 灰色决策方法及应用研究[D]. 南京: 南京航空航天大学, 2010. Song Jie. Research on the methods of grey decisionmaking and its application[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.

[3] 郑彤, 蔡龙飞, 王志刚, 等. 地形匹配辅助导航中匹配区域的选择[J]. 中国惯性技术学报, 2009, 17(2): 191-196. Zheng Tong, Cai Long-fei, Wang Zhi-gang, et al. Selection of matching area in terrain match aided navigation[J]. Journal of Chinese Inertial Technology, 2009, 17(2): 191-196.

[4] Pedrycz W, Song M L. Analytic hierarchy process(AHP) in group decision making and its optimization with an allocation of information granularity[J]. Fuzzy System, 2011, 19(3): 527-539.

[5] Luo Dang, Zhou Ling, Shi Yanan, et al. The study of multi-objective grey situation decision method[C]//EProduct E-Service and E-Entertainment. 2010: 1-4.

[6] 谌剑, 张静远, 李恒, 等. 基于灰色决策的地形辅助导航区域选取方法[J]. 海军工程大学学报, 2012, 24(5): 48-53. Shen Jian, Zhang Jing-yuan, Li Heng, et al. Selection criteria for matching area of terrain aided navigation based on gray decision-making[J]. Journal of Naval University of Engineering, 2012, 24(5): 48-53.

[7] 蔡体菁, 陈鑫巍. 基于层次分析法的重力匹配区域选择准则[J]. 中国惯性技术学报, 2013, 21(1): 93-96. Cai Ti-jing, Chen Xin-wei. Selection criterion based on analytic hierarchy process for matching region in gravity aided INS[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 93-96.

[8] 夏冰, 蔡体菁. 基于SPSS的重力匹配区域选择算法[J]. 中国惯性技术学报, 2010, 18(1): 81-84. Xia Bing, Cai Ti-jing. Gravity matching regions selection by statistical product and service solutions[J]. Journal of Chinese Inertial Technology, 2010, 18(1): 81-84.

[9] Zhou Y Y, Zhang Y S, Guo L, et al. Simulation of geomagnetic/inertial integrated navigation system[C]// 2011 Third International Conference on Measuring, Technology and Mechatronics. 2011, vol.3: 253-256.

[10]Zhou J M, Ju Z W. Multi-elements decision-making method based on grey decision model and analytic hierarchy process[C]//2011 International Conference on Remote Sensing, Environment and Transportation Engineering. 2011: 3288-3291.

[11]Kung C Y, Wen K L. Applying grey relational analysis and grey decision making to evaluate the relationship between the company attributes and its financial performance[J]. Decision Support System, 2007(3): 842-852.

[12]Wang Jian-qiang. Multi-criteria decision making approach based on gray linguistic judgment matrix[M]. Chengdu: Modern Business Trade Industry, 2009.

Selection for matching area in terrain aided navigation based on entropy-weighted grey correlation decision-making

XU Xiao-su1,2, TANG Jun-jun1,2, ZHANG Tao1,2, YUE Zeng-yang1,2
(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University, Nanjing 210096, China; 2. School of Instrument Science & Engineering, Southeast University, Nanjing 210096, China)

In view that traditional selection methods of matching area in terrain aided navigation has the problem of incomplete evaluation due to using only one characteristic parameter, a novel selection criteria is presented based on entropy weighted gray relational decision-making, in which the influences of terrain parameters such as standard deviation, roughness, entropy and correction are comprehensively considered. First, the gray decision matrix was constructed according to the calculated parameter values. Second, the decision matrix was handled dimensionlessly and then normalized to get the gray relational matrix. Finally, a comprehensive selection criterion was developed after calculating the weights of each parameter by using entropy value method as objective weighting. The simulation results show that the matching error of terrain-aided navigation is smaller in the areas with higher evaluation values.

terrain aided navigation; terrain information; matching area; entropy weighted; grey correlation decision-making

U666.1

A

1005-6734(2015)02-0201-06

10.13695/j.cnki.12-1222/o3.2015.02.012

2014-10-15；

2015-01-23

国家自然科学基金项目（51175082，61473085，51375088）；微惯性仪表与先进导航技术教育部重点实验室基金；优秀青年教师教学科研资助计划（2242015R30031）

徐晓苏（1961—），男，博士生导师，从事测控技术与导航定位领域的研究。E-mail：xxs@seu.edu.cn