基于单轴旋转INS/GPS组合姿态误差观测的垂线偏差测量方法

戴东凯，王省书，战德军，吴 伟，黄宗升

（国防科学技术大学 光电科学与工程学院，长沙 410073）

基于单轴旋转INS/GPS组合姿态误差观测的垂线偏差测量方法

戴东凯，王省书，战德军，吴 伟，黄宗升

（国防科学技术大学 光电科学与工程学院，长沙 410073）

单轴旋转INS/GPS组合导航系统的姿态误差直接受垂线偏差的影响，因此利用对单轴旋转INS/GPS组合的姿态误差观测也可实现垂线偏差的估计。首先，利用INS中的三个激光陀螺构建了激光陀螺组合体（LGU）并进行自主姿态测量，以LGU作为姿态基准以获取INS/GPS组合的姿态误差。然后，建立垂线偏差测量的观测方程和状态方程。最终采用Kalman滤波/平滑算法同时实现垂线偏差和其他系统误差的最优估计。通过对状态变量精确、合理地建模，并利用全球重力模型补偿垂线偏差信号的低频分量，从而实现垂线偏差与系统误差的解耦。通过仿真验证了该方法的可行性, 仿真所用的航迹由实测数据生成。仿真结果表明该方法能够有效地测量垂线偏差的高频扰动量。由于该方法的测量精度依赖于所采用的陀螺性能，采用角随机游走较小的陀螺可以获得较好的垂线偏差测量结果。船载实验结果表明，该方法测量得到的垂线偏差数据重复性精度优于0.5″。

垂线偏差；单轴旋转INS；GPS；激光陀螺组合体

垂线偏差是指地球上某点的真实重力矢量与正常重力矢量在方向上的偏差[1]。垂线偏差含有丰富的重力场高频信息，相比重力异常，它更能反映重力场的精细结构[2]。在资源勘探、地震和火山监测、卫星精密轨道、重力辅助导航以及高精度惯性导航等应用中，对高精度、高分辨率垂线偏差信息有着极为迫切的需求。

传统的垂线偏差获取方法主要有两种：一是天文大地测量方法，即利用天文经纬仪或数字天顶相机观测恒星以确定垂线偏差[3]。该方法虽然精度极高，但是操作繁琐，效率较低，且只能在陆地使用，不适用于海上大动态、大范围的垂线偏差测量活动。二是重力异常计算方法。该方法是利用卫星重力仪或标量航空重力仪测定区域内的重力异常数据，再通过Vening-Meinesz积分公式[1]计算垂线偏差。其缺点在于所需的高质量重力异常数据较多，数据利用率不高，所获取的垂线偏差精度和分辨率也较为有限[4]。

基于INS/GPS组合的垂线偏差动态方法是获取高精度、高分辨率垂线偏差数据的有效手段。该测量方法可以弥补重力异常计算方法精度和分辨率上的不足，克服地面静态测量方法效率低下的缺陷，是测量精度与测量效率相平衡的一种测量方案。目前，国际上利用INS/GPS组合实现垂线偏差动态测量的主流技术方案是“直接求差法”[5-7]。其基本原理是：利用惯性传感器或惯性导航系统直接敏感比力信息，同时利用GPS测量干扰加速度，将比力与干扰加速度做差即可得到重力矢量，进而计算得到垂线偏差。该方法面临两大难题：一是扣除干扰加速度的影响。20世纪90年代初，载波相位差分GPS技术的发展成功地解决了测量载体运动速度和加速度高精度测量的问题，干扰加速度对惯性测量的影响基本可以消除。二是需要提供高精度的水平基准。高精度水平姿态基准的获取是制约垂线偏差测量精度的关键问题，垂线偏差的存在会引起INS/GPS组合导航系统的姿态误差，而INS/GPS姿态误差也会导致相应的垂线偏差测量误差，因此垂线偏差与惯性姿态基准无法解耦[8]。

INS/GPS组合导航姿态误差直接受垂线偏差的影响[9]，基于此现象文献[10]提出利用星敏感器和激光陀螺组合体（Laser Gyroscope Unit，LGU）提供姿态基准以测量INS/GPS组合的姿态误差，进而获取垂线偏差的方法。该方法能够有效地解决传统方法中垂线偏差与组合导航姿态误差耦合的问题，然而LGU中存在的由初始姿态误差和陀螺误差引起的姿态误差仍无法完全消除。此外，由于该方法需要使用星敏感器，测量只能在晴朗的夜晚进行，且要求载体的运动平稳，严重限制了该方法的使用。本文旨在对文献[10]的方法进行改进，提出一种基于INS/GPS组合姿态误差观测的垂线偏差测量新方法。与文献[10]中的方法相比，新方法有两方面的改进：一是仅利用LGU构建姿态基准，无需利用星敏感器，因而拓展了测量的适用条件，降低系统的成本和复杂度；二是对LGU姿态误差进行精确的建模，并利用Kalman滤波实现垂线偏差与LGU姿态误差的分离。

本文从理论上建立了所提出的垂线偏差测量方法的状态方程和观测方程，给出垂线偏差测量的实现方案。通过仿真验证算法的可行性，研究该测量方法对惯性器件精度的需求。最后通过船载实验对垂线偏差测量的重复性进行验证。

1 基于INS/GPS姿态误差观测的垂线偏差测量方法

首先定义东北天（E-N-U）坐标系为导航坐标系，即n系。在该坐标系中，原点O位于测量位置，z轴沿着参考椭球的法线指向椭球外部，也就是与O点处正常重力矢量的方向相反（在近地面处忽略正常重力线的弯曲效应）；x轴指向东向；y轴指向北向，并与其他两轴构成正交右手坐标系。

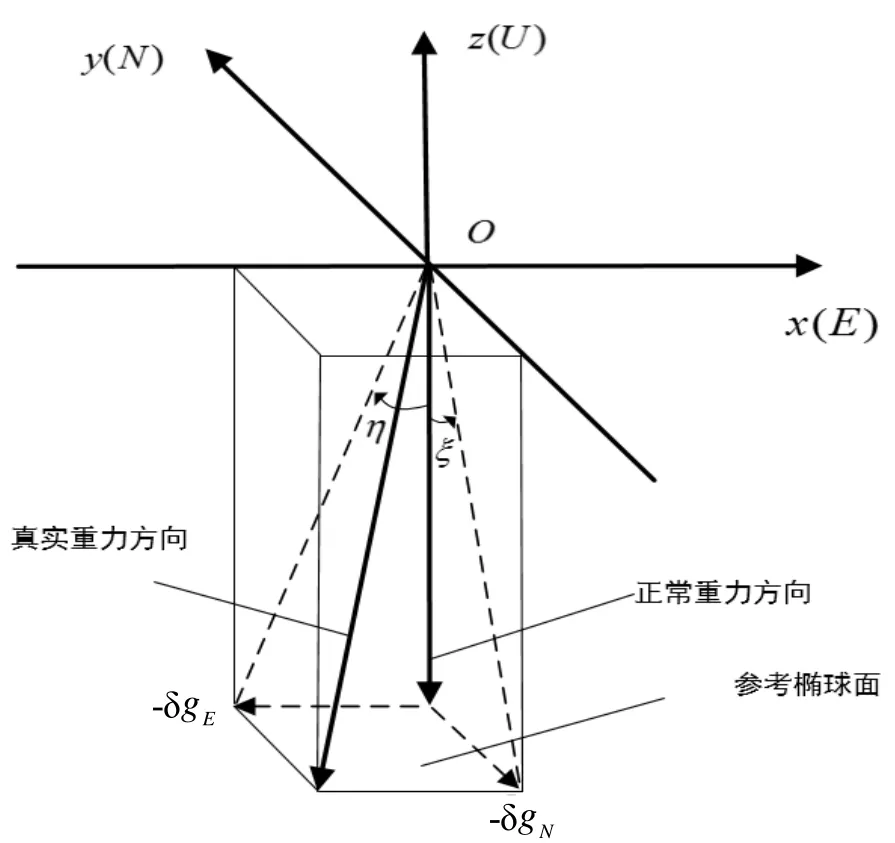
图1 坐标系与垂线偏差的定义Fig.1 Definitions of the coordinates and DOVs

东向和北向重力扰动分别记为δgE(东向为正方向)和δgN(北向为正方向)。垂线偏差的北-南和东-西角度分量分别记为ξ和η，他们直接与重力扰动矢量的水平分量相关，并定义为：

式中，g是正常重力的大小。在小角度近似条件下, 式(1)和(2) 可近似写为：

文献[11]从理论和仿真分析了垂线偏差对INS/ GPS组合导航姿态误差的影响，分析结果表明垂线偏差与INS/GPS组合导航姿态误差存在以下关系：

从以上关系可知，通过观测INS/GPS的姿态误差即可实现垂线偏差的测量。

1.1 观测方程的建立

为了获取INS/GPS的姿态误差，需要提供一个高精度的姿态基准。文献[10]提出用INS中的三个激光陀螺构建激光陀螺组合体（Laser Gyroscope Unit，LGU）。在给定初始姿态值后，LGU可以自主地测量本体坐标系（b系）相对于地球坐标系（e系）的姿态[12]，利用GPS提供的位置信息可以进一步获取LGU相对于n系的姿态，以LGU的姿态输出作为姿态基准获取INS/GPS组合的姿态误差。获取INS/GPS姿态误差观测量的流程图如图2所示。

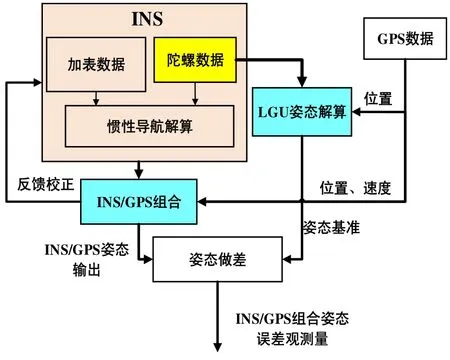
图2 INS/GPS姿态误差观测量的获取流程Fig.2 Procedure for obtaining the observation of INS/GPS integration error

为了便于实施，LGU姿态初始值由INS/GPS组合导航提供。INS/GPS的姿态输出存在误差，将引入到LGU的初值中。在LGU姿态解算中，初始误差和陀螺误差将引起较大的姿态误差，因此利用INS/GPS组合与LGU的姿态差中包含了INS/GPS姿态误差信息和LGU姿态误差信息。为了获取垂线偏差信号，关键在于如何有效地消除LGU姿态误差的影响。

INS/GPS与LGU的姿态差可以由下式给出：

式中：ΔΘ为INS/GPS与LGU的姿态差，nδΦ为INS/GPS在n系下的姿态误差，nδψ为LGU在n系下的姿态误差。其东向和北向分量可以表示为：

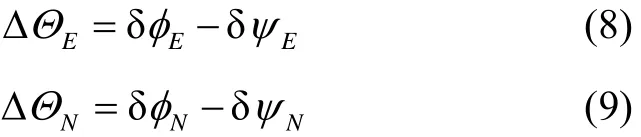
式中：ΔNΘ和ΔEΘ为INS/GPS与LGU姿态差的北向和东向分量；δNφ和δEφ为INS/GPS姿态误差的北向和东向分量; δNψ和δEψ为LGU姿态误差 的北向和东向分量。

将式(5)(6)代入式(8)(9)可得：

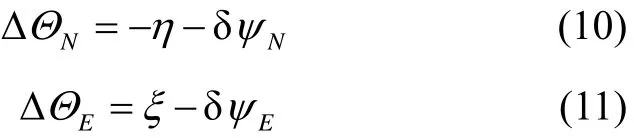
式中：ΔNΘ和ΔEΘ可以直接利用INS/GPS和LGU的姿态输出计算得到。式(10)(11)即为垂线偏差估计的观测方程。

为了利用INS/GPS和LGU姿态差的观测信息实现垂线偏差的最优估计，下面将对垂线偏差信号和LGU姿态误差进行状态空间建模。

1.2 状态方程的建立

LGU姿态的误差方程[12]在地球坐标系下可以描述为：

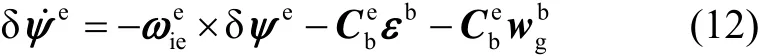
式中：δψe为LGU在e系下的姿态误差；εb为陀螺在b系下的零偏,为陀螺在b系下的高斯白噪声。陀螺零偏可以用随机常值过程建模：

由于GPS可以提供高精度的位置数据，因此LGU相对于e系的姿态可以转换到n系下。LGU在n系下的姿态误差方程可以相应的表示为：

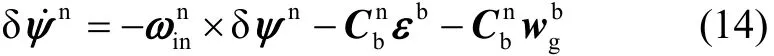
由式(14)可以看出，LGU姿态误差主要是由陀螺误差和LGU姿态误差的初始值引起的。由式(14)不难发现，LGU姿态误差受到地球转动角速度矢量的调制，而地球的旋转周期为24 h，因此LGU的姿态误差将表现为低频误差的特性。另一方面，垂线偏差在长波（低频）区域内也具有较强的功率谱，因此其长波分量很容易与LGU的姿态误差耦合。

为了避免对垂线偏差进行统一建模，我们将垂线偏差分解为如下两个部分：

将式(15)和(16)代入式(10)和(11)，则式(10)和(11)可以重新整理后得到：

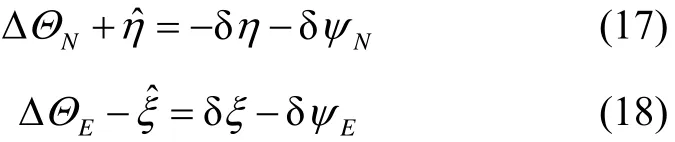
式(17)和(18)为新的观测方程。

为了使LGU姿态误差和与垂线偏差扰动不产生耦合，要求对垂线偏差扰动建模的随机过程其功率谱在低频区域内有极低的增益，以使低频系统误差不会引入到垂线偏差扰动估计结果中。

2阶Gauss-Markov过程常用于垂线偏差扰动的建模[15]。然而，该模型在低频区仍然有一定的增益。本文采用2阶Gauss-Markov过程的导数[17]对垂线偏差扰动进行建模。与2阶Gauss-Markov模型相比，本文所提出的模型在低频区域内功率谱密度有更强烈的衰减，因而能实现垂线偏差与系统误差在频域上的解耦。δη和δξ的模型可以写成状态空间的形式如下：

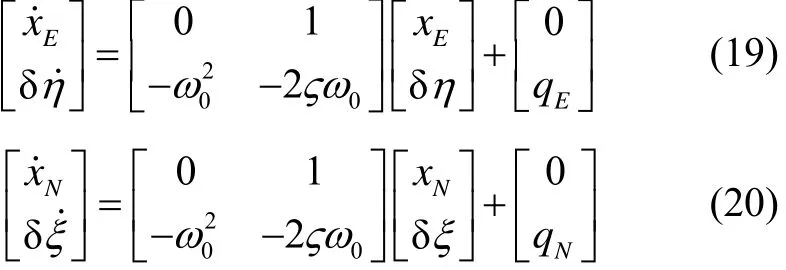
式中：xE和xN为中间变量，其导数即为垂线偏差扰动；0ω为固有频率，它与载体的航速有关；ς为阻尼系数；qE和qN为相应模型的过程噪声。

用于垂线偏差扰动估计所选用的状态空间矢量如式(21)所示，其状态空间模型可由式(13)(14)(19)以及式(20)给定。

最后，δη和δξ可以由以上给出的状态空间模型和观测方程，利用Kalman滤波/平滑算法估计得到。将δη、δξ与、合并即为最终的垂线偏差测量值。

2 仿真与分析

2.1 仿真条件

本节将通过仿真验证本文方法的可行性。仿真采用导航级的惯性测量单元，且只考虑常值零偏误差和高斯白噪声误差。惯性器件和GPS的误差参数如表1所示。本文的INS采用的是单轴旋转调制结构[18]，以消除由于惯性器件零偏缓慢变化引起的系统导航误差。在组合导航中，通过旋转调制解构可以提高惯性器件误差的可观测性，进而抑制测量误差，提高测量精度。

仿真中测量船的姿态和速度由海上试验的实测数据给出，利用实测的姿态、速度数据生成用于仿真的陀螺、加表数据。测量船的船姿、船速、船位变化分别如图3～5所示。

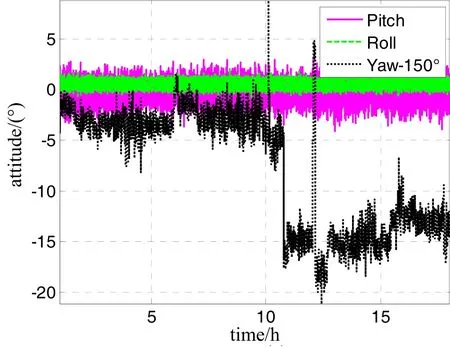
图3 仿真航迹中的船体姿态Fig.3 Ship attitude on the trajectory in simulation

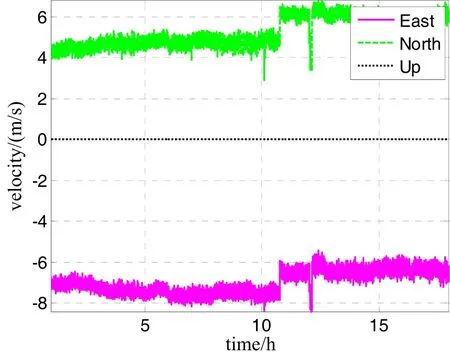
图4 仿真航迹中的船体Fig.4 Ship velocity on the trajectory in simulation

图5 船体的航行轨迹Fig.5 Trajectory of the ship

用于生成仿真数据的重力扰动矢量是从美国公布的其本土的高精度垂线偏差模型DEFLEC12中得到的。该模型的垂线偏差精度和分辨率均高于EGM2008重力模型，能够更精确地反映重力场的精细结构。如图4所示，为了能够利用DEFLEC12模型，仿真时将船位的初始点平移至经度240°，纬度34°的位置。EGM2008相对于DEFLEC12模型的差值如图6所示，可以看到在某些区域内（山地），EGM2008中包含较大的扰动误差。

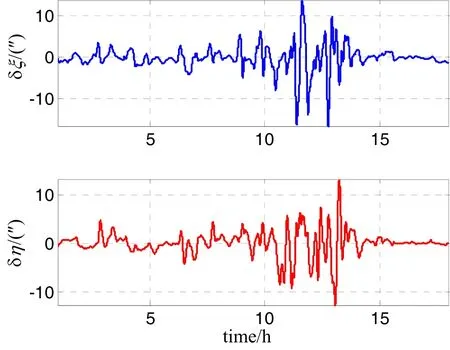
图6 航迹上EGM2008垂线偏差误差的分布Fig.6 Distribution of EGM2008 DOV errors along-track

2.2 仿真结果与误差分析

利用对INS/GPS的姿态误差的观测实现垂线偏差测量的可行性是以垂线偏差与INS/GPS组合姿态误差满足式(5)和式(6)的关系为基础的，即δφE-ξ=0，δφN+η=0。图7给出了仿真得到的δφE-ξ和δφN+η随时间的变化，可以看到，其数值均在0附近振荡，且振荡的幅值较小，因此INS/GPS姿态误差能够较好地反映垂线偏差扰动的变化。然而，在垂线偏差变化较为剧烈的区域（第10～14 h），INS/GPS姿态误差对垂线偏差扰动的跟踪误差较大。

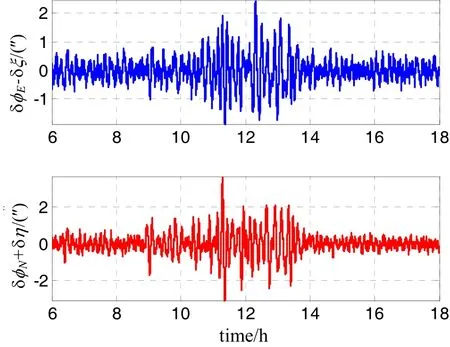
图7 INS/GPS姿态误差与垂线偏差扰动的关系Fig.7 Relationship between the attitude errors of INS/GPS and DOV disturbances

图8为LGU姿态基准的误差变化，由于初始姿态误差和陀螺误差的影响，LGU的姿态存在较大的误差，并表现为低频趋势的形式。

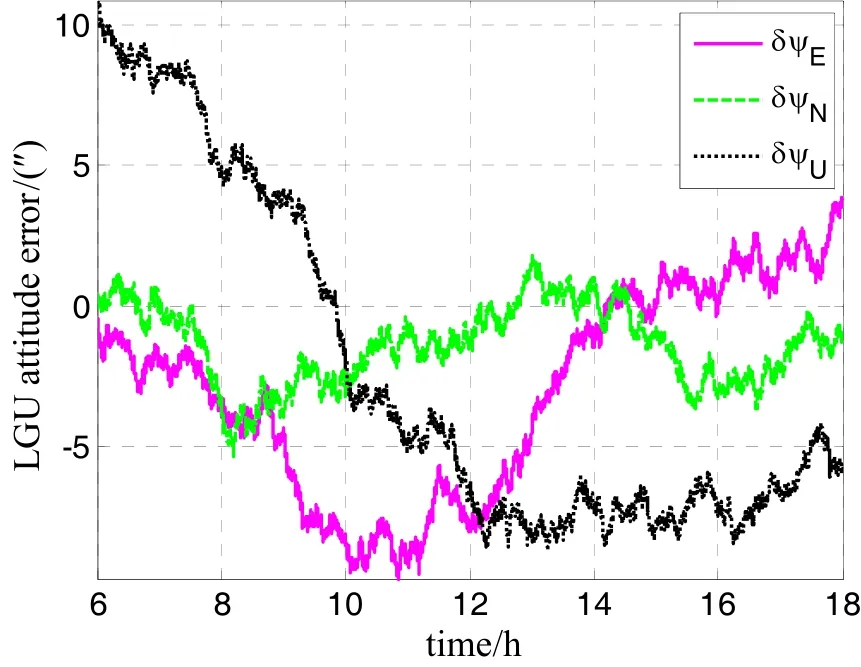
图8 LGU姿态基准误差Fig.8 Errors of attitude reference provided by LGU

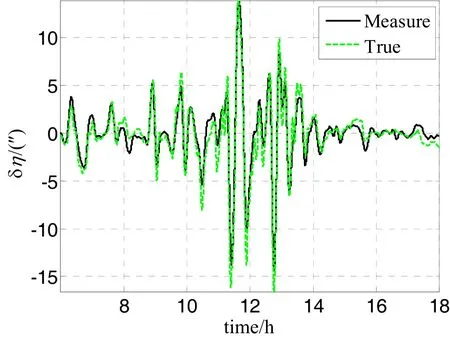
图9a 垂线偏差扰动的测量结果Fig.9a DOV disturbance measurement result

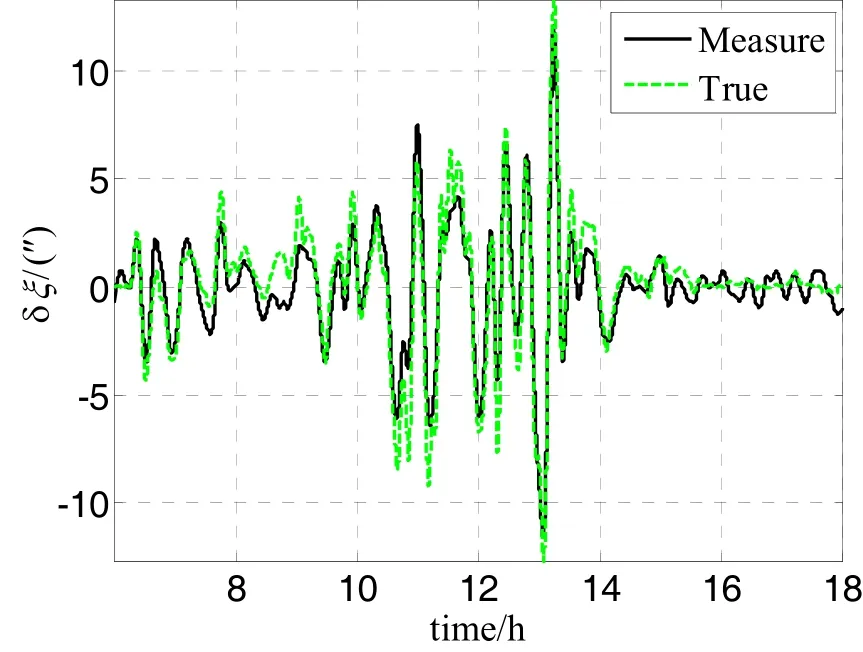
图9b 垂线偏差扰动的测量结果Fig.9b DOV disturbance measurement result

利用本文所述的方法对垂线偏差进行估计，最终的垂线偏差测量结果如图9a、9b所示（前6 h的数据用于INS的精对准，不用于垂线偏差测量）。可以看到，测量得到的垂线偏差扰动为垂线偏差的高频扰动信息，它能够更好地反应重力场的细节信息。在本文方法中，垂线偏差的低频部分由EGM2008提供，在测量时不对它进行估计，然而由于EGM2008在低频区域内仍然存在一定的误差，因此这一误差将直接引入到最终测量结果中。

由图8可以看到，LGU姿态误差主要由陀螺零偏误差和初始姿态误差引起的，并表现为低频误差的特性，因此在频域上与垂线偏差扰动几乎没有混叠。然而，陀螺的角度随机游走(Angular random walk, ARW)引起的LGU姿态误差中仍然存在一些高频成分，这部分高频扰动误差有可能会引入到垂线偏差扰动的测量结果中。为了进一步验证方法的可行性，本文仿真了不同陀螺角度随机游走条件下的垂线偏差测量结果，仿真结果如图10所示。由图10可以看出，随着陀螺ARW系数的增大，垂线偏差测量的误差也会相应的增大。因此，本文的垂线偏差测量方法要求所采用的惯导系统具有较低的陀螺角随机游走误差。

图10 垂线偏差测量误差与角随机游走的关系Fig.10 DOV measurement error with respect to ARW

3 实验结果

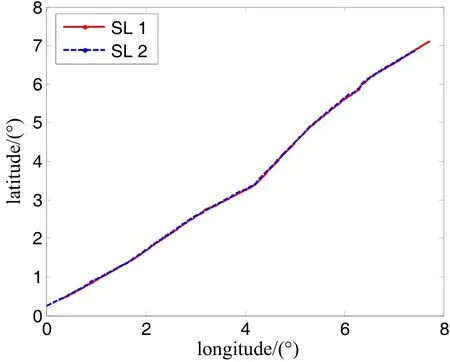
图11 测量船的航迹Fig.11 Trajectory of the survey ship

为验证本文方法的有效性，课题组于2014年在中国近海进行了船载测量实验。如图11所示，在测量的海域内有两条重复的测线，我们将其命名为测线1 (SL1) 和测线2 (SL2)。在SL1测线上，测量船朝西南方向行驶，在SL2上测量船的行驶方向则朝向东北，每条测线的总长度约为900 km。

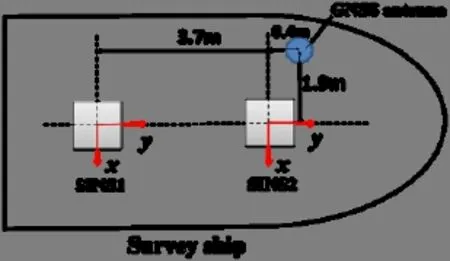
图12 线偏差测量的系统安装图Fig.12 System configuration for DOV measurement

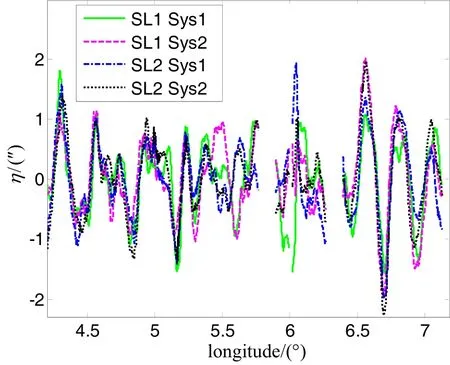
图13a 四组垂线偏差高频量测量结果的对比（东-西分量）Fig.13a Comparison between four sets of high-frequency DOV measurement (east-west)

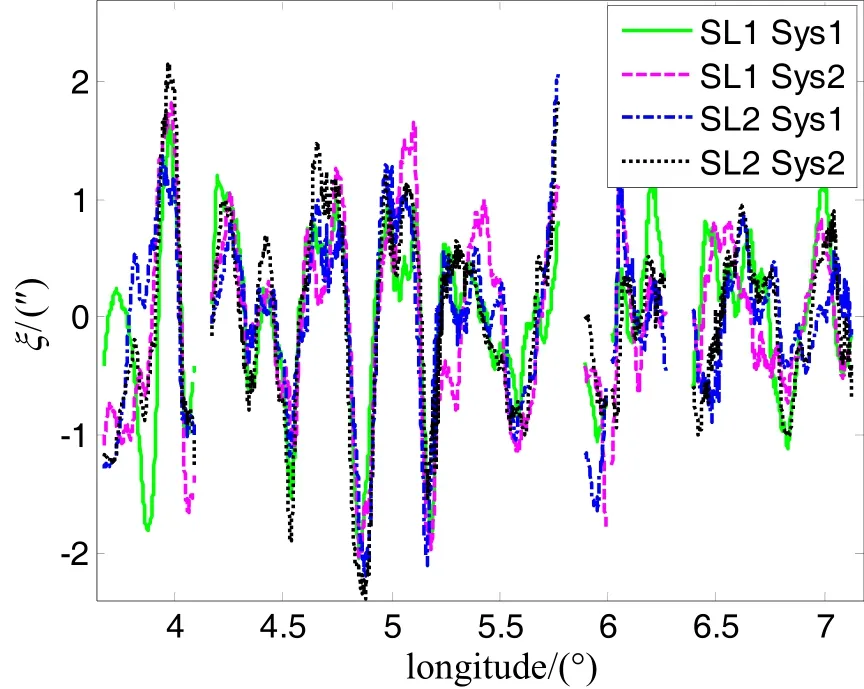
图13b 四组垂线偏差高频量测量结果的对比（北-南分量）Fig.13b Comparison between four sets of high-frequency DOV measurement (north-south)

如图12所示，在测量船上安装有两套激光陀螺捷联式惯性导航系统，即SINS1和SINS2，捷联惯导的数据采样率为1000 Hz。此外，船上还安装有GNSS接收机（包括一个GNSS天线）用于获取速度和位置信息。其定位精度为2 m，速度精度是0.03 m/s。GNSS数据的采样率为1 Hz。SINS1与GNSS构成的组合导航系统命名为系统1（Sys1），SINS2与GNSS的组合则命名为系统2（Sys2）。

采用本文所提出的垂线偏差测量算法对两套系统在SL1和SL2测线上采集得到四组实验数据进行处理，通过四组实验数据估计得到的垂线偏差扰动结果如图13a、13b所示（为了更清楚地表现测量细节信息，图中只显示了经度从3.5°～7°范围内垂线偏差扰动的测量结果）。可以看到，所估计得到垂线偏差扰动在0附近波动，其幅值约为2″。四次测量得到的垂线偏差扰动的重复性如表2所示，从表中可以看到，四次测量结果的重复性精度优于0.5″。

表2 四次测量的重复性精度Tab.2 Repeated accuracies of four sets of DOV data

4 结 论

本文提出一种垂线偏差动态测量的新方法。由于单轴旋转INS/GPS组合导航系统的姿态误差直接受垂线偏差的影响，本文方法通过对单轴旋转INS/GPS组合的姿态误差观测以实现对垂线偏差的估计。利用真实的船摇数据生成仿真航迹，通过仿真验证本文方法的可行性。仿真结果表明本文方法能够有效地测量垂线偏差的高频扰动量，以获取更精细的地球重力场信息。该方法的测量精度依赖于所采用的陀螺性能，采用低角随机游走性能的激光陀螺可以获得较好的垂线偏差测量结果。通过实验验证该方法的有效性，结果表明该方法的垂线偏差测量重复性精度优于0.5″。

（References）：

[1] Moritz H. Physical geodesy[M]. Bad Vöslau, Austria: SpringerWienNewYork, 2005.

[2] Hirt C, Marti U, Bürki B, et al. Assessment of EGM2008 in Europe using accurate astrogeodetic vertical deflections and omission error estimates from SRTM/DTM2006.0 residual terrain model data[J]. Journal of Geophysical Research, 2010, 115(B10404).

[3] Hirt C, Bürki B, Somieski A, et al. Modern determination of vertical deflections using digital zenith camera[J]. Journal of Surveying Engineering-Asce, 2010, 136(1): 1-12.

[4] 黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005.

[5] Kwon J H, Jekeli C. A new approach for airborne vector gravimetry using GPS-INS[J]. Journal of Geodesy, 2001, 74: 690-700.

[6] Li X, Jekeli C. Ground-vehicle INS/GPS vector gravimetry[J]. Geophysics, 2008, 73(2): 11-21.

[7] Cai S, Zhang K, Wu M, et al. Improving airborne strapdown vector gravimetry using stabilized horizontal components[J]. Journal of Applied Geophysics, 2013, 98: 79-89.

[8] Senobari M S. New results in airborne vector gravimetry using strapdown INS/DGPS[J]. Journal of Geodesy, 2010, 84(5): 277-291.

[9] 李胜全, 欧阳永忠, 常国宾, 等. 惯性导航系统重力扰动矢量补偿技术[J]. 中国惯性技术学报, 2012. 20(4): 410-413. Li Sheng-quan, Ouyang Yong-zhong, Chang Guo-bin, et al. Compensation technology of gravity disturbance vector in inertial navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 410-413.

[10] Dai D K, Wang X S, Zhan D J, et al. An improved method for dynamic measurement of deflections of the vertical based on the maintenance of attitude reference[J]. Sensors, 2014, 14(9): 16322-16342.

[11] 战德军, 戴东凯, 张忠华, 等. 单轴旋转INS/GPS组合导航中重力垂线偏差引起的姿态误差分析[J]. 中国惯性技术学报, 2014, 22(3): 301-305. Zhan De-jun, Dai Dong-kai, Zhang Zhong-hua, et al. Analysis of gravity vertical deflection-induced attitude error in single-axis rotation INS/GPS integrated navigation system[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 301-305.

[12] Wei M, Schwarz K P. A strapdown inertial algorithm using an Earth-fixed Cartesian frame[J]. Navigation, Journal of the Institute of Navigation, 1990, 37(2): 153-167.

[13] Pavlis N, Holmes K A, Kenyon S C, et al. The development and evaluation of the EGM2008[J]. Journal of Geophysical Research, 2012, 117(B04406): 1-38.

[14] Harriman D W, Harrison J C. A statistical analysis of gravity-induced errors in an airborne INS[C]//AIAA Guidance and Control, conference, 1984: 285-295

[15] Kriegsman B A, Mahar K B. Gravity-model errors in mobile inertial-navigation systems[J]. Journal of Guidance, 1986, 9(3): 312-318.

[16] Leonard J M, Nievinski F G, Born G H, et al. Gravity error compensation using second-order gauss Markov processes[J]. Journal of Spacecraft and Rockets, 2013, 50(1): 217-229.

[17] Gibbs B P. Advanced Kalman Filtering, least-squares and modeling[M]. New Jersey: John Wiley & Sons, INC., 2010.

[18] 龙兴武, 于旭东, 张鹏飞, 等. 激光陀螺单轴旋转惯性导航系统[J]. 中国惯性技术学报, 2011, 18(2): 149-153. Long Xing-wu, Yu Xu-dong, Zhang Peng-fei, et al. Single-rotating inertial navigation system with ring laser gyroscope[J]. Journal of Chinese Inertial Technology, 2011, 18(2): 149-153.

Measurement of dynamic vertical deflections by observing attitude errors of single-axis rotation INS/GPS system

DAI Dong-kai, WANG Xing-shu, ZHAN De-jun, WU Wei, HUANG Zong-sheng
(College of Opto-Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Since the attitude errors of INS/GPS integrated system are directly related to deflections of the vertical (DOVs), it is expected that DOVs can also be estimated via the observation of INS/GPS attitude errors. In this paper, a laser gyroscope unit (LGU) is constructed by three laser gyroscopes of the INS, and used as an attitude reference for calculating INS/GPS attitude errors. Then, the observation equation and state-space equations for DOV measurement are accurately modeled. Finally, the DOVs and systematic errors are simultaneously estimated by a Kalman filter/smoother. The DOVs and systemic errors are decoupled since the state-space variables are accurately and properly modeled, and the long-wavelength components of DOVs are well compensated by a global gravity model. The feasibility of the proposed method are validated by simulation. Simulation results also show that this method can measure the high-frequency disturbances of DOVs efficiently. As the measurement accuracy of this method depends on the performance of gyroscope, a better accuracy of DOV measurement can be achieved when the gyroscopes with low angular random walk are adopted. The shipborne experiment results show that the repeated accuracy of the DOV measurement method is better than 0.5″.

deflection of the vertical; single-axis rotation INS; GPS; laser gyroscope unit

U666.1

A

1005-6734(2015)02-0172-07

10.13695/j.cnki.12-1222/o3.2015.02.007

2014-11-15；

2015-03-11

国家自然科学基金（61275002）

戴东凯（1986—），男，博士研究生，从事光电仪器与测控技术研究。E-mail：daidongkai@nudt.edu.cn

联 系 人：王省书（1963—），女，教授，博士生导师，从事光电仪器与测控技术研究。