激光捷联惯组静、动态安装精度理论计算分析
2015-03-10杨朋军雷志学杨瑞超
杨朋军,雷志学,李 良,杨瑞超
(西安航天精密机电研究所,西安710100)
激光捷联惯组静、动态安装精度理论计算分析
杨朋军,雷志学,李 良,杨瑞超
(西安航天精密机电研究所,西安710100)
由于试验技术条件的限制,激光捷联惯组的静、动态安装精度一直无法用试验方法测试。通过理论计算的方法,对某型号激光捷联惯组静、动态安装精度满足总体指标的情况予以详细说明。该理论分析方法对其他型号安装精度理论分析具有一定的指导意义。
安装精度;计算;分析
0 引言
激光捷联惯组系统作为惯性坐标基准,广泛应用于各种运载火箭、导弹及其他飞行器中,其工作精度和可靠性直接影响飞行器的飞行精度。因此,总体任务书对激光捷联惯组的静、动态安装精度一直都有比较严格的指标要求。但是,由于试验技术条件的限制,惯组的静、动态安装精度一直无法用试验方法测试,因此只能通过理论计算方法予以分析[1]。
总体要求某型号激光捷联惯组安装于大梁后,其静态安装误差不大于3′,动态安装误差不大于9′。本论文从影响激光捷联惯组的静、动态安装精度的因素,如惯组的质心偏离减振中心的程度、减振器静、动态条件下的角变形、惯组结构件的精度等方面对激光捷联惯组静、动态安装精度满足总体技术要求情况予以详细说明。
1 激光捷联惯组介绍
某型号激光捷联惯组由被减振部分、减振器、安装环等部分组成,惯组在弹体上安装时,安装环的定位面与安装大梁定位基准面靠紧,惯组本体被减振部分通过减振器连接在安装环上,再通过安装环固定在弹体上。由于减振器是一个弹性支撑,惯组本体和安装环通过减振器连接之后,可能由于减振器的扭转、变形产生安装误差。惯组的安装精度,实际上是保证惯组台体定位面和相应安装环定位面之间的平行度。为了保证惯组安装精度,设计了惯组装调工装,其工作示意图如图1所示。

图1 惯组安装示意图Fig.1 The installation of IMU
惯组被减振部分安装时,将惯组安装环定位面与调试工装板上对应定位面紧靠,本体被减振部分置于减振器上,然后将台体定位面通过螺钉与调试工装板相应定位面紧固,减振器与台体的连接先不紧固,通过使用装调销钉限制减振器在紧固过程中的扭转,保证惯组台体和安装环之间的平行后,再紧固减振器固定螺母。
2 惯组静、动态安装精度分析
影响惯组静、动态安装精度因素其实分为两部分:一部分为安装环安装面的加工误差导致的安装环相对弹体大梁的角变形;一部分为静、动态环境下,由于惯组质心偏离,惯组减振器在被减振部分受外力作用下,因其质心偏离产生角变形,从而导致被减振部分相对安装环的角变形。下面分别从安装环的加工精度、惯组本体静平衡、减振器角变形等方面予以分析。
2.1 惯组安装环精度分析
零、部件安装面作为被测量要素相对于惯组标定定位面(基准),其位置度偏差θ计算有一经验公式,表示为
(1)
式中:θ表示位置度偏差,单位为(″);
δ表示被测要素设计位置度累计公差,单位为mm;
l表示被测要素尺寸,单位为mm。
惯组安装环安装基准面平面度为0.06mm,安装环安装基准面跨度为330mm×332mm,通过式(1)可得安装环在弹上的安装误差角θ1=37.5″。
2.2 惯组被减振部分静平衡[2]
惯组本体采用4个三向减振器绕本体X轴对称布置减振器方式。如果惯组本体被减振部分的质心O和4个减振器组成的减振中心不重合,那么在惯组受到外界激励时,就会有绕相应轴角运动的趋势。当受到周期激励时,这种转动也是周期性的,从而产生振动附加角速率。因此为了减小惯组的振动附加角速率,就须对惯组本体进行静平衡,尽可能保证惯组本体被减振部分的质心O和4个减振器组成的减振中心重合。通过对惯组进行静平衡,测出惯组惯组被减振部分质心与惯组减振中心距离见表1所示。

表1 惯组被减振部分质心偏离减振中心距离Tab.1 The distance of the center of mass of the damping part off the damping center of the IMU
2.3 减振器刚度分析计算[3]
减振系统总刚度、系统共振频率和放大倍数存在以下关系:
(2)
(3)
式中:fn表示共振频率(Hz);
ωn表示无阻尼系统固有频率;
η表示结构损耗因子;
T表示共振放大倍数。

惯组减振系统共振频率fn=45Hz、共振放大倍数T=2.5,将所有已知条件代入式(2)、式(3)可得减振系统总动刚度
K=1.51×106(N/m)
减振器动态修正系数d的取值范围为1.3~2.8,取d=2.0[4],因此减振器静刚度
Kj=7.6×105(N/m)
2.4 惯组静态安装精度分析[5]
惯组减振系统示意图如图2所示。
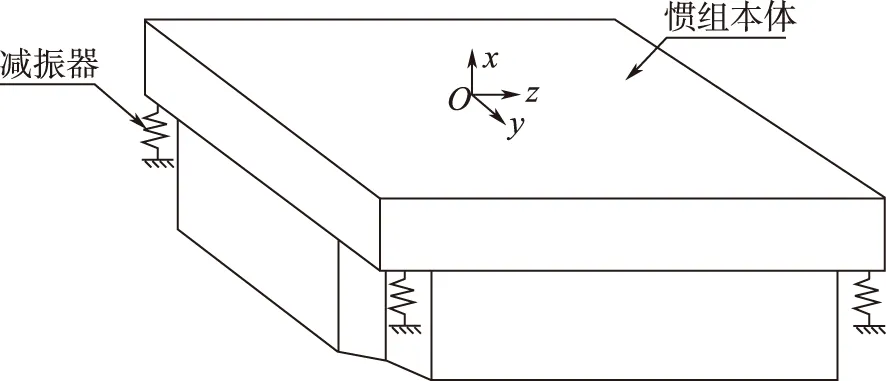
图2 惯组减振系统示意图Fig.2 Vibration reduction system of the IMU
惯组静态环境下,减振器角变形是由减振器的刚度、减振器的跨度、惯组被减振部分质心偏离减振中心的程度等因素引起的。
为了减小惯组被减振部分相对下安装件(惯组安装面)角变形,保证惯组安装精度及振动导航精度,减振器在装配前对每个减振器进行了一致性筛选,从而保证惯组4个减振器静刚度一致。在减振器刚度、减振器跨度一定的前提下,惯组被减振部分的质心、偏离减振中心的程度以及外加载荷的大小便是引起惯组被减振部分相对下安装件(惯组安装面)角变形的关键影响因素。
静态条件下,惯组被减振部分的角变形就是在1g重力作用条件下,惯组被减振部分相对安装环的角变形。由于重力方向垂直向下,因此水平方向偏心量最大的部分便是引起惯组被减振部分静态角变形的关键因素。图3为惯组静态条件下角变形示意图。
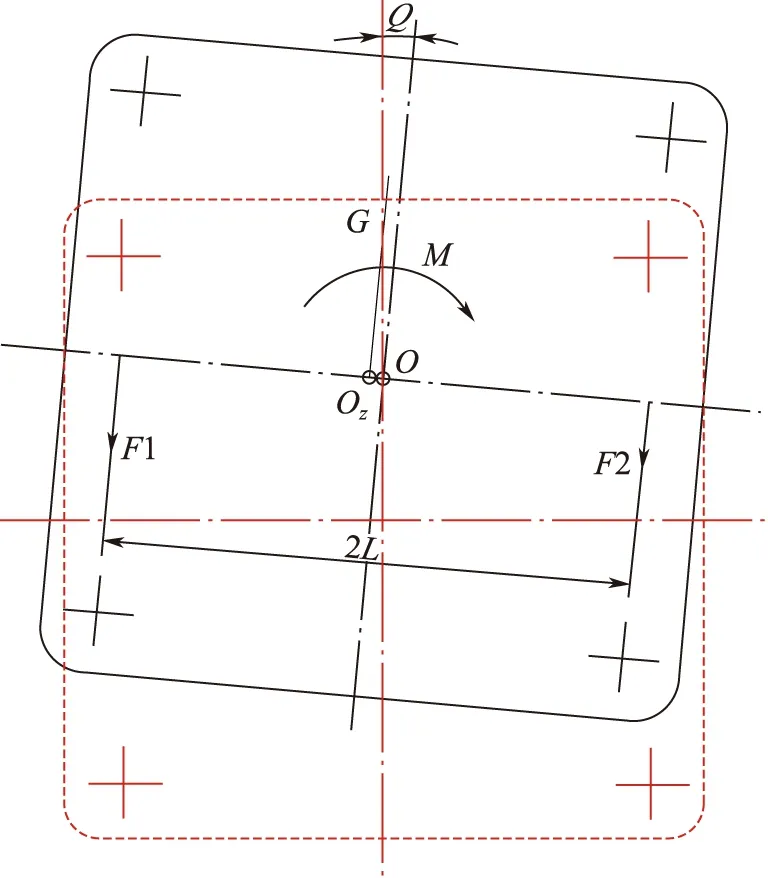
图3 惯组静态条件下角变形示意图Fig.3 Angular deformation of the IMU under static condition
图3中:G为作用在惯组质心Oz的作用力;
M为作用力产生的扭矩;
F1、F2为减振系统支反力,其中F1>F2;
L为支反力到惯组中心距离;
θ为角变形量。
根据力矩平衡关系,可得静态条件下如下公式
1g×m×d=Kj/2×b×L
(4)
式中: b表示静态条件下减振系统变形量的差值;
Kj表示减振器的静刚度;
d表示质心偏离减振中心距离;
L表示支反力到惯组中心距离。
将减振系统静刚度Kj=7.6×105(N/m),L=124mm,m=19.8kg,d=1.18mm带入式(4)可得b=5.13×10-3mm。由此可计算出在静态安装时,惯组被减振部分的角变形θ2=arcsin(b/L)=2.3×10-3(°)≈8.12″。
惯组静态安装精度就是安装环机械加工误差和1g作用力条件下,惯组被减振部分相对安装环安装面角变形之和,即θ=θ1+θ2≈46″,满足小于3′技术要求。
2.5 惯组动态安装精度分析
动态环境下,惯组被减振部分质心为O,减振器支反力作用点为P;假定每个减振器力学性能相同,在惯组承受动态惯性力为G时,每个减振器对惯组的支反力为F,惯组减振系统承受外界水平动态激励时,受力示意图如图4所示。

图4 惯组水平激励受力示意图Fig.4 Stress of the IMU under horizontal excitation
在动态环境条件下,由于惯组在每个方向都有一定的偏心,惯组被减振部分就会绕与受力方向垂直的另外两个轴偏转。惯组在X向偏心量最大,而减振系统三向刚度相同,那么在三向受外界力相同情况下,就会导致Y向受力时绕Z轴或者Z向受力时绕Y轴产生的角变形最大。下面就以Y向受力时绕Z轴为例,计算惯组静态时的角位移。由于偏心量远小于支撑距离,所以可以认为减振系统反作用力的力臂相等。
惯组被减振部分在动态条件下,可得同式(4)相似关系
G×d=K/2×b×L
(5)
式中: G表示惯组承受动态惯性力;
K表示减振器动刚度。
通过上述已知条件,可以得出惯组在48g动态条件下,惯组被减振部分的角变形θ2=197.2″。
惯组动态安装精度就是安装环机械加工误差和动态条件下,惯组被减振部分相对安装环安装面角变形之和,即θ=θ1+θ2≈235.3″,满足小于9′技术要求。
3 结论与意义
本文以某型号激光惯组为研究对象,通过从质心偏离减振中心的程度、减振器静、动态条件下的角变形、惯组结构件的精度等方面对激光捷联惯组静、动态安装精度满足总体技术要求情况进行了分析。通过本文的工作可以得到以下结论:
1)在惯组质量、环境条件确定的前提下,惯组的静、动态安装精度与质心偏离减振中心的程度成正比,质心偏离程度越小,惯组的静、动态安装精度越小;
2)要提高惯组的静、动态安装精度,除适当提高结构件的机械精度外,更重要的是提高减振器的刚度,增加减振器的跨度。
本文提供的方法和结论对以后同类型惯组系统的结构和减振系统设计具有重要的参考意义。
[1] 张树侠,孙静.捷联式惯性导航系统[M].北京:国防工业出版社,1987.
[2] 杨朋军.激光捷联惯组静平衡试验报告[R].中国航天科技集团公司第九研究院十六研究所,2011,4.
[3] 王佳民,裴听国.惯性平台新型金属橡胶减振器理论与实验研究[J].宇航学报,2003,24(1):92-96.
[4] 戴德沛.阻尼技术的工程应用[M].北京:清华大学出版社,1991.
[5] 杨朋军.激光捷联惯组结构设计研制总结报告[R].中国航天科技集团公司第九研究院十六研究所,2011,11.
Theoretical Analysis and Calculation on Dynamic and Static Installation Precision of Laser Strapdown IMU
YANG Peng-jun,LEI Zhi-xue,LI Liang,YANG Rui-chao
(Xi’an Aerospace Precision Electromechanical Onstitute,Xi’an 710100,China)
Due to the limitation of experimental conditions,dynamic and static installation precision of laser strapdown Inertial Measurement Unit(IMU)has been unable to test with the method of experiment.In this paper,the dynamic and static installation precision of a kind of IMU has been elaborated through the method of theoretical calculation.The theoretical analysis method used in this paper would be a guidance for the analysis on installation precision of other types of IMU.
Installation precision;Calculation;Analysis
2015 - 04 - 14;
2015 - 04 - 16。
杨朋军(1979 - ),男,硕士,高级工程师,主要从事精密仪器与机械分析与设计。
E-mail:abcyangpengjun@126.com
TH113
A
2095-8110(2015)05-0001-04
