具有随机时滞和异步相关噪声的非线性系统的高斯滤波器设计

2015-06-05宋申民

中国惯性技术学报 2015年2期

关键词：将式时滞高斯

于浛，宋申民，王硕，李鹏

（1. 哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨 150001； 2. 湘潭大学信息工程学院，湘潭 411100）

具有随机时滞和异步相关噪声的非线性系统的高斯滤波器设计

于浛1，宋申民1，王硕1，李鹏2

（1. 哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨 150001； 2. 湘潭大学信息工程学院，湘潭 411100）

针对随机时滞和异步相关噪声情况下的状态估计问题，提出了一种改进的高斯滤波算法(GF)，并给出了其适用于高维系统的实现形式—随机时滞和异步相关容积卡尔曼滤波器(CKF-RDCN)。首先，通过满足Bernoulli分布的互不相关随机序列，来描述系统观测数据中可能存在的随机时滞现象，将量测噪声作为状态变量用以实现对观测时滞后验概率密度的估计。其次，利用一阶斯特林插值公式来近似估计，由于过程噪声和量测噪声异步相关，而导致的含有随机变量的多维积分问题。最后，依据三阶球径容积法则，给出了CKF-RDCN滤波算法的详细设计。此外，经典GF算法是所提出的改进GF算法的特例，其作为一个通用的非线性滤波算法框架，根据不同的后验概率密度估计方法，可以有不同的实现形式。仿真结果表明，相比于扩展卡尔曼滤波算法(EKF)以及容积卡尔曼滤波算法(CKF)，CKF-RDCN在解决含有观测时滞和相关噪声系统的状态估计问题时，具有更高的精度和更好的数值稳定性。

非线性滤波；高斯滤波；随机时滞；相关噪声；容积卡尔曼滤波

非线性系统的状态估计在空间卫星交会对接[1]、无人机导航[2]、信号处理[3]以及金融分析[4]等领域具有重要的应用价值与广阔的应用前景。它对导航系统参数精度的高低具有重要的影响，在导航领域里对该问题的研究一直是热点问题。

作为非线性滤波算法中应用最为广泛的扩展卡尔曼滤波器(EKF)[5]，由于其简洁的形式和高效的计算性能，早在20世纪70年代就有学者将其应用于飞行器导航中，并指出系统的非线性特性极大地影响着导航参数的确定[6]。然而，由一阶泰勒展开而建立的EKF算法具有精度不高的先天缺陷[7]。因此，随着人们对高精度导航的需求越来越高，对非线性滤波算法的研究便也越来越深入。

由Ito等[8]提出的高斯滤波算法(GF)是其中具有里程碑意义的非线性状态估计算法。GF以高斯噪声为假设前提，采用贝叶斯估计方法构建了关于非线性离线系统的最优滤波框架，将复杂的概率密度计算问题简化为高斯加权积分的计算。其重要意义在于，为非线性系统状态估计问题的解决设计了一个具有普遍意义的框架，通过采用不同的高斯加权积分算法可以设计相应的滤波算法。例如，基于高斯厄尔米特正交法则的高斯厄尔米特滤波算法(GHQF)[8]，基于无迹变换的无迹卡尔曼滤波算法(UKF)[7]，基于斯特林多项式插值的差分滤波算法(DDF)[9]，基于球径容积法则的容积卡尔曼滤波算法(CKF)[10]，以及近年来提出的基于稀疏网格的稀疏网格正交滤波器(SGQF)[11]。其中，针对单纯激光导航系统反应慢且精度低的问题，Jung等[12]提出了一种融合激光、陀螺以及编码器的组合导航系统，并采用UKF算法进行位姿估计；胡高歌等[13]针对SINS/BDS组合导航系统中噪声统计特性未知的情况，提出了一种改进的UKF算法，达到自适应估计的目的；Jwo等[14]将DDF滤波算法应用于GPS导航估计问题中，所设计的算法既满足高动态下对高精度导航的要求，又适用于低动态下的估计特性；由于INS/GPS组合导航系统本质是非线性系统，孙枫等[15]为提高导航精度，将具有高精度估计特性的CKF算法应用于INS/GPS组合导航中。此外，对于近年来提出的SGQF算法，其在飞行器的视觉导航问题中也有应用[16]。

然而，上述滤波算法均是建立在同一假设条件下，即要求系统过程噪声和量测噪声是相互独立的。但随着工作环境对导航设备的影响，加之元器件老化、数据处理能力受限等原因[17-19]，在实际系统的应用中，可能存在噪声相关与传感器量测时滞的现象。对噪声相关条件下的状态估计问题，其解决方法一般可分为两类：一类是在原有卡尔曼类型滤波器的基础上，采用相关噪声解耦的方法使问题转化为标准的滤波问题[20-23]；一类是给出解决此类问题的通用框架，提出新的噪声相关条件下的GF算法[24]。文献[20]采用构造伪状态方程的方式，来达到相关噪声解耦的目的，并给出了在EKF框架下的实现方法。Chang[21]采用了相同的相关噪声解耦方式，给出了其在UKF框架下的解决方案，并利用高斯条件分布，分离线性化子结构的方式，来降低UKF算法的计算负担。王小旭等[22]根据最小均方误差估计准则，推导了噪声相关条件下的UKF滤波形式。最近，徐小良等[23]在量测噪声和过程噪声相关的条件下，又考虑了过程噪声互相关的情况，以构造伪状态方程与矩阵相似变化相结合的方式，达到噪声解耦的目的。相比于噪声解耦较为丰富的研究成果，针对适用于噪声相关条件下的通用滤波框架的研究较少。Wang等[24]以两步更新后验概率密度替代原有滤波框架中一步更新的方式，来实现噪声解耦。对于量测时滞问题，Hermoso等[25]以量测噪声为状态增量，采用一阶泰勒近似和无迹变换的方式估计状态的条件均值和协方差阵，并给出EKF和UKF时滞滤波器。随后，Hermoso等[26]又针对两步随机时滞问题，提出了相应UKF下的解决方法。Wang等在文献[24]基础上，考虑随机时滞问题，提出了适用于随机时滞和同步相关噪声系统的GF滤波算法[27]。

目前，对于导航系统中可能存在的含有随机时滞和噪声异步相关情况下的最优估计算法的研究还不够完善。受文献[27]启发，研究了具有随机时滞和异步相关噪声情况下的最优估计问题，提出了一种可以通用的新型高斯滤波框架，并给出了其在三阶球径容积法则下的实现形式——随机时滞和异步相关容积卡尔曼滤波器(CKF-RDCN)。此外，还提出了一种基于一阶斯特林插值的，关于随机变量多维积分的近似估计算法，用以实现新型高斯滤波器的设计，从而为高精度导航参数的确定提供相应的理论基础。

1 GF滤波算法

考虑如下含有加性噪声的非线性离散系统

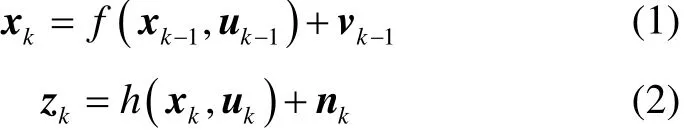
式中：xk∈ℝn表示系统在k时刻的状态；zk∈ℝm表示系统在k时刻的量测值；uk∈ℝnu表示系统在k时刻的输入；vk-1和nk为不相关零均值高斯白噪声，其协方差矩阵分别为Qk-1和Rk。

以Zk=[…]T表示系统在时刻1到k所获得的观测序列，N表示高斯分布，则GF滤波算法框架如下[8]：

时间预测

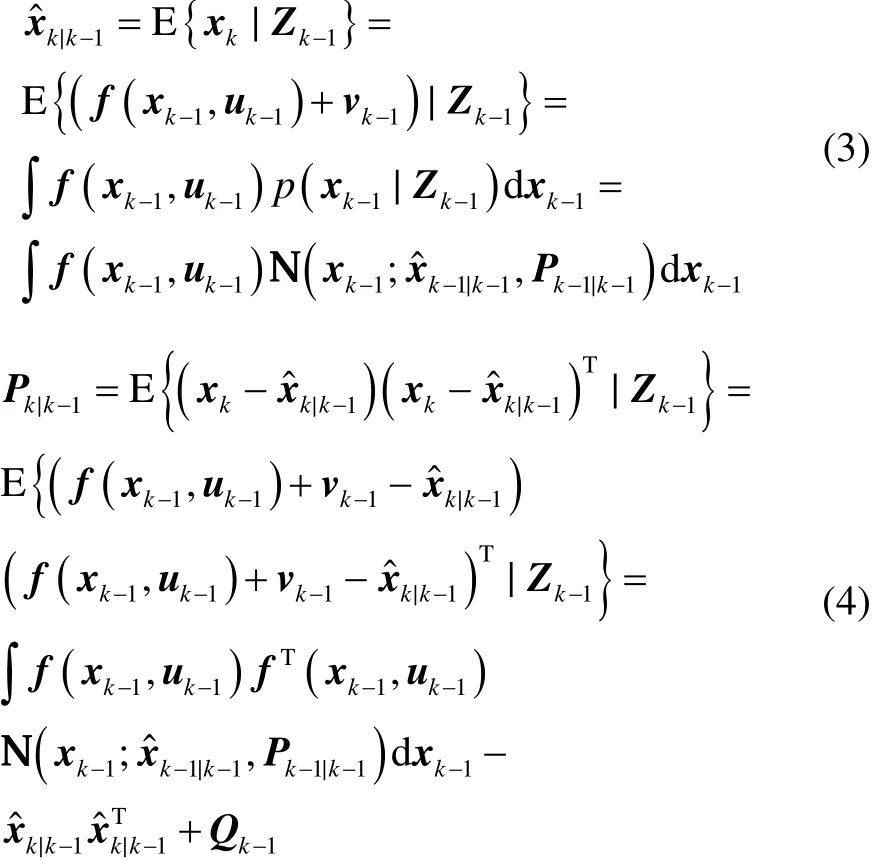
量测更新

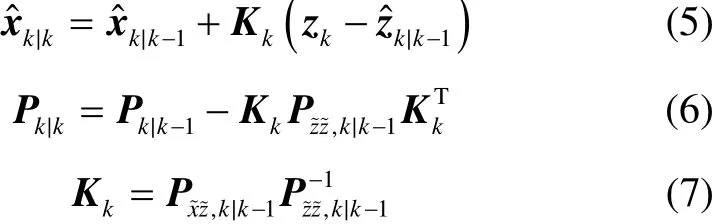
其中，

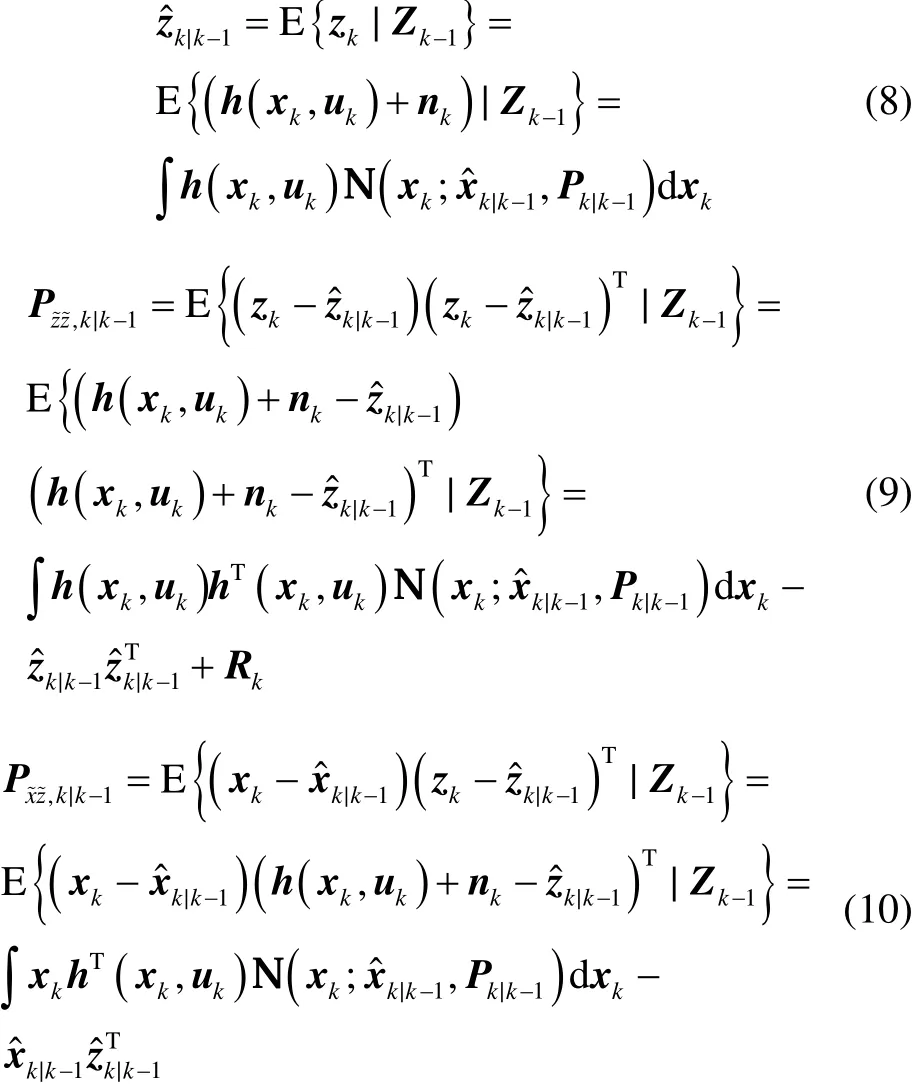
2 改进GF滤波算法

由上述分析可知，标准GF滤波算法是建立在过程噪声和量测噪声互不相关这一假设的基础上，且未考虑观测数据具有随机时滞的情况。在本节中，提出一种改进的GF滤波算法，用以解决系统中存在噪声相关和随机时滞的问题。在式(1)和式(2)所构成的离散系统模型基础上，考虑如下假设条件。

假设1 过程噪声vk-1和量测噪声nk为异步相关噪声，满足

式中：δkl表示克罗内克函数；Sk≠0表示过程噪声和量测噪声间的互协方差阵。

假设2 系统中数据传输存在随机时滞情况，即观测方程重新构建为：

式中：εk（k＞1）为满足Bernoulli分布的互不相关的随机序列，且满足统计概率：

其中，

与标准GF滤波算法框架类似，提出的改进的GF滤波算法同样由时间预测和量测更新两个部分构成。

2.1 时间预测

定理1 在假设1和假设2条件下，给定滤波器在k-1时刻状态量的估计值以及方差值，则关于k时刻的一步预测值k|k-1和Pk|k-1分别为：

证明：因为过程噪声vk-1与观测序列Yk-1不相关，所以

由于nk是零均值高斯白噪声，且nk与观测序列Yk-1不相关，所以式(19)和式(20)显然成立。

此外，由下述的分析可知，状态量xk的估计值与状态增量在k-1时刻互协方差阵的一步预测值无关。因而，在所提出的改进GF滤波算法中，并未涉及对方差阵Pxn,k|k-1的计算。

2.2 量测更新

引理1[9]考虑非线性函数y=f（x），那么根据一阶斯特林插值公式，在点处函数y近似取值为：

式中：Δxd表示向量Δx=x-的第d个元素；Sd表示协方差矩阵平方根分解后的第d列向量；m取为插值区间的一半。

定理2 在假设1和假设2条件下，给定滤波器在k时刻的观测值yk以及状态量在k-1时刻的估计值和方差值，则关于k时刻状态量xk的估计值和方差值分别为

其中，

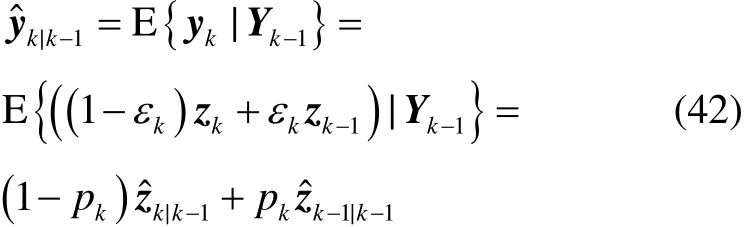
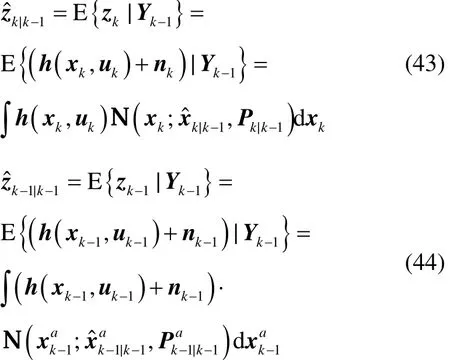
其次，

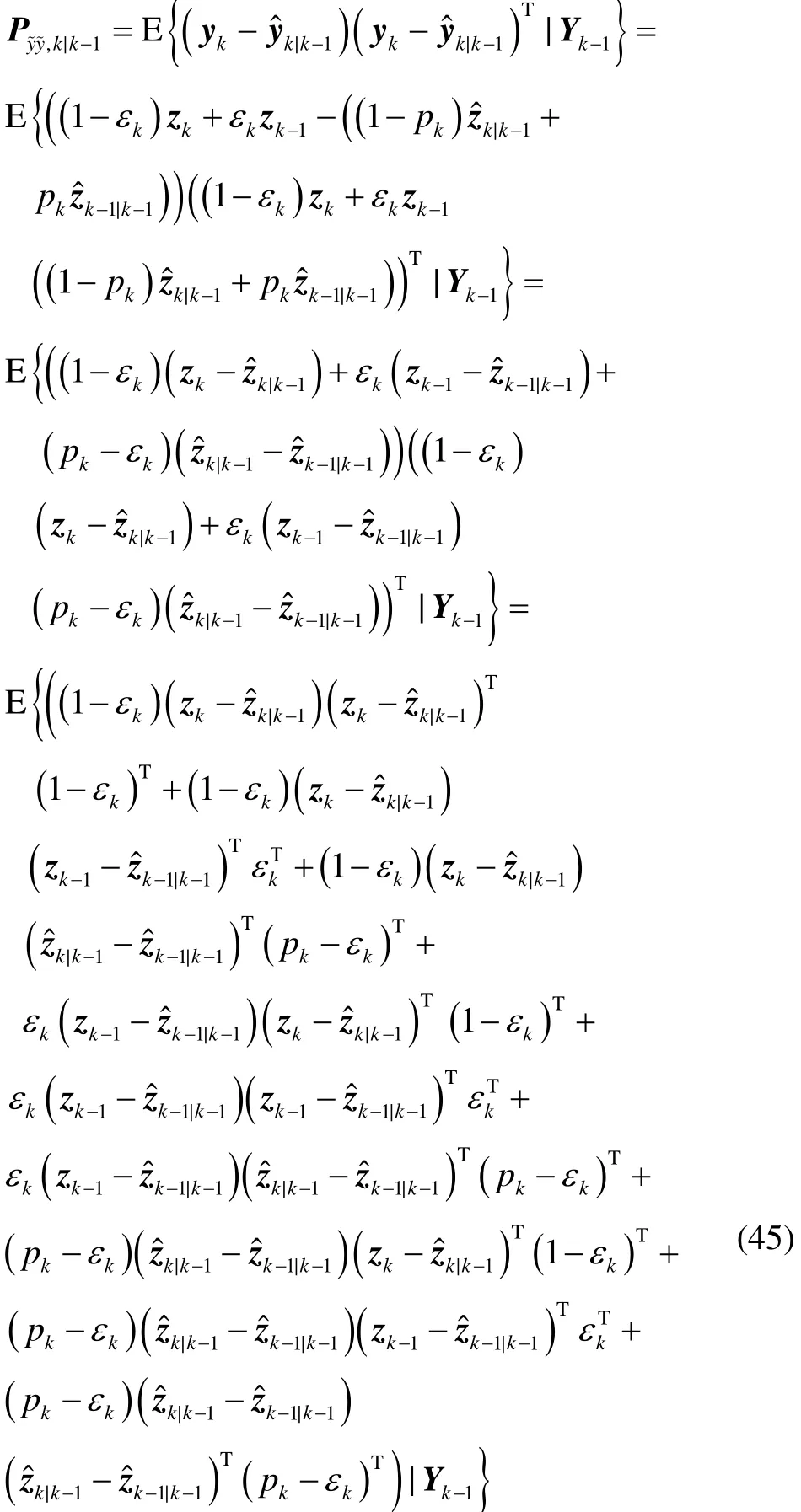
由于

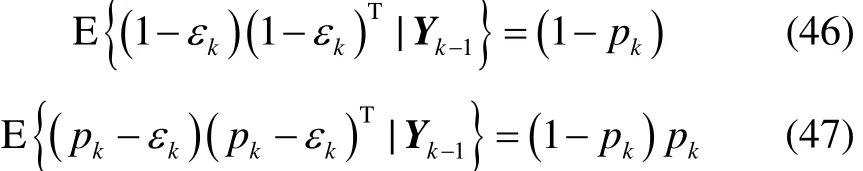
将式(43)、式(44)、式(46)以及式(47)代入到式(45)中，得式(34)。根据Pzz,k|k-1定义，可得：

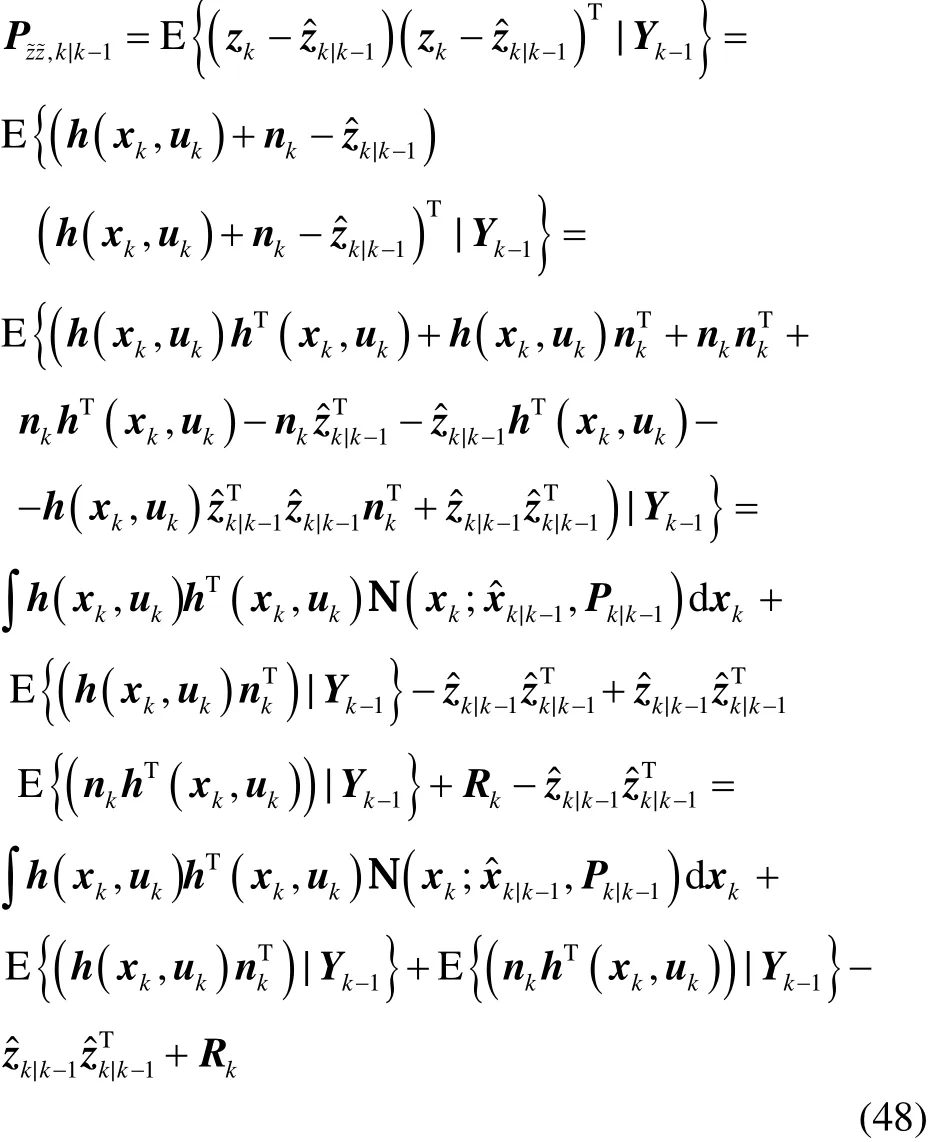
由于在假设1条件下，状态量xk中含有的过程噪声vk-1与量测噪声nk相关，因而E{(h(xk,uk))|Yk-1}及E{(nkhT(xk,uk))|Yk-1}均不为零。文献[28]中指出，对于E{(h(xk,uk))|Yk-1}和E{(nkhT(xk,uk))|Yk-1}的计算是处理异步相关问题最为棘手的问题，但其并没有给出一种有效的解决方法。根据引理1，非线性函数h（xk,uk）可近似为：

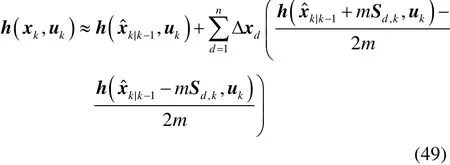
式中：Δxd表示向量Δx=xk-k|k-1的第d个元素；Sd,k表示协方差矩阵Pk|k-1平方根分解后的第d列向量。将式(49)代入E{(h(xk,uk))|Yk-1}，可得：

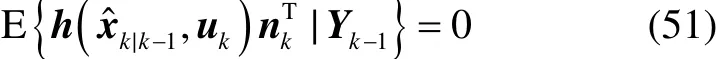
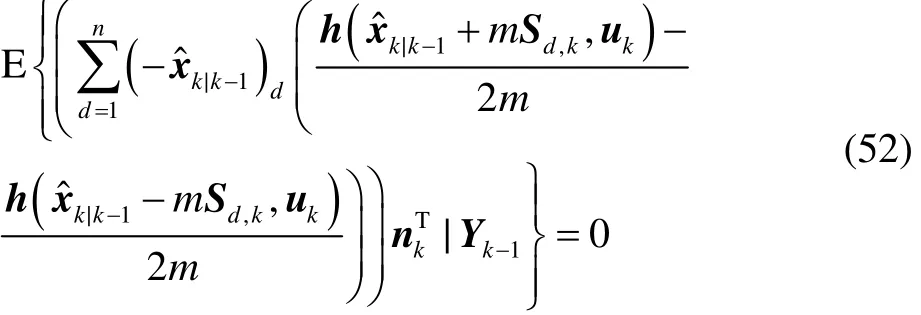
将式(1)、式(51)和式(52)代入到式(50)中，得：式中：Mk定义同式(36)。

又由于（h（xk,uk））T=nkhT（xk,uk），因此：

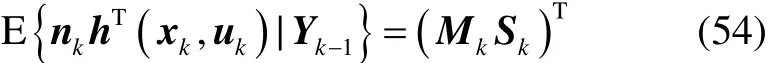
将式(53)和式(54)代入式(48)中，得式(35)。

根据Pzz,k-1|k-1定义，可得：

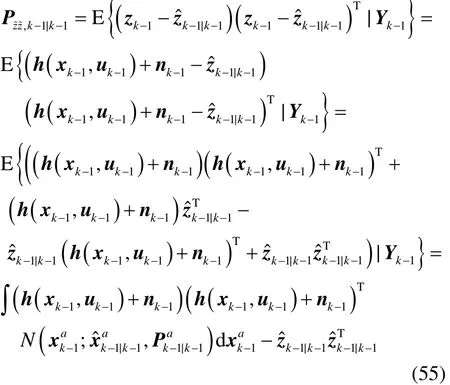
式(37)得证。

将式(12)和式(31)代入到Pxy,k|k-1中，可得：

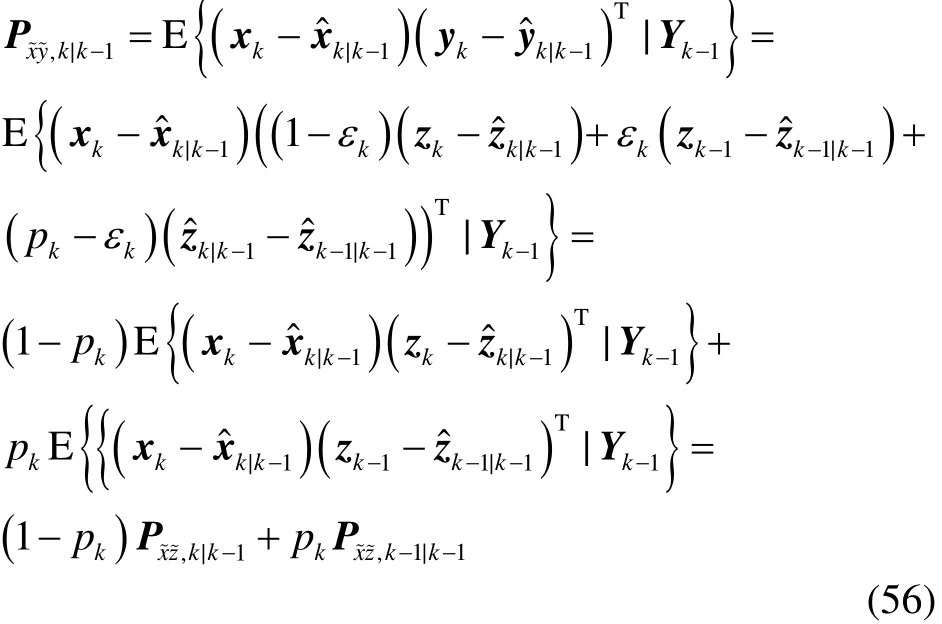
式(38)得证。

将式(2)代入到Pxz,k|k-1中，可得：

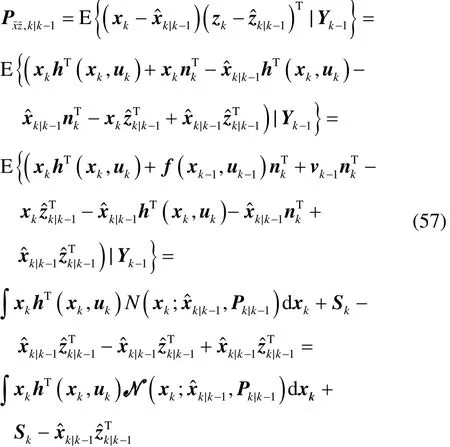
式(39)得证。

将式(1)和式(2)代入到Pxz,k-1|k-1中，可得：

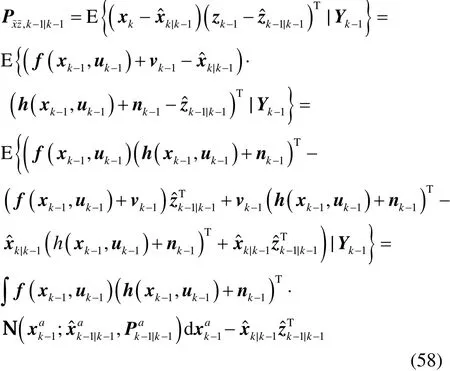
式(40)得证。

根据文献[29]，易得式(27)、式(28)以及式(29)。然而由于假设1的存在，使得对式(29)中Pny,k|k-1的估计与文献[29]给出的结果有所不同。下面给出Pny,k|k-1的估计结果。将式(12)和式(31)代入到Pny,k|k-1中可得：

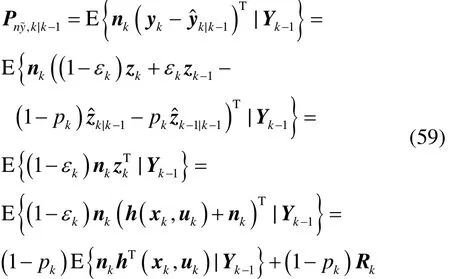
将式(54)代入到式(59)中，得式(41)。

最后，将式(24)和式(27)代入Pxn,k|k中：

由于

因此式(60)等价于

式(30)得证。

3 CKF-RDCN滤波算法

分析定理1和定理2可知，对多维高斯加权积分的计算是所设计的改进GF滤波算法实现过程中需要解决的主要问题。由前文叙述可知，针对这一问题可以采用数值积分的方法来近似计算，例如，斯特林多项式插值、无迹变换以及球径容积法则等。同其他方法相比，球径容积法则具有较好的数值稳定性，且精度较高，因而给出基于三阶球径容积法则的改进GF滤波算法的实现形式——CKF-RDCN滤波算法。

3.1 三阶球径容积法则

考虑如下形式的多维高斯加权积分：

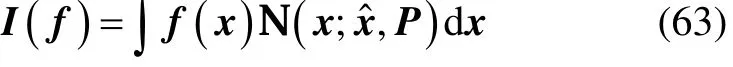
式中：x∈ℝn，且服从均值为，方差为P的高斯分布。则根据三阶球径容积法则，式(63)可近似为：

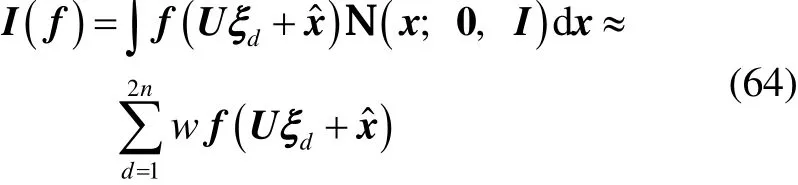
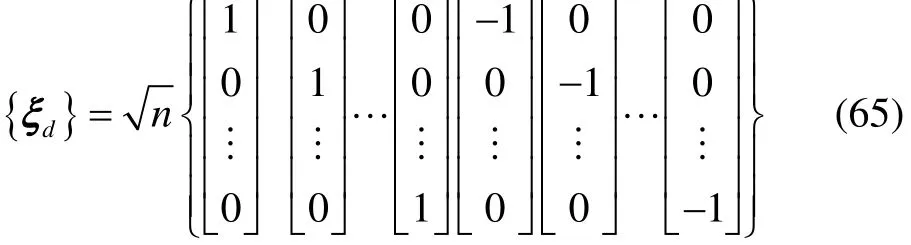
3.2 CKF-RDCN滤波算法

时间预测

其中，ξi,L表示L×2L维容积点集的第i列向量。

量测更新

式(32)、式(33)、式(35)、式(37)、式(39)以及式(40)可近似为：

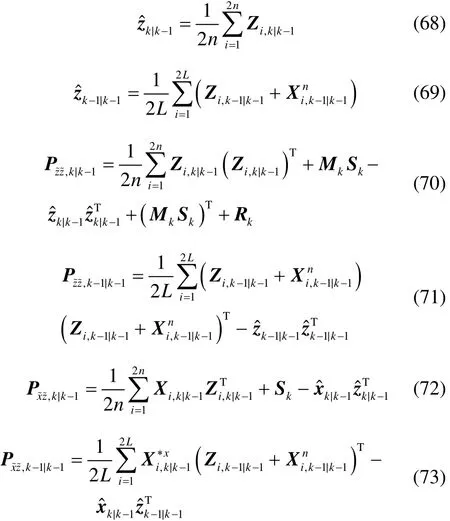
式中：

其中，Xi,k|k-1为由时间预测的计算结果k|k-1和Pk|k-1变换后的容积点，即

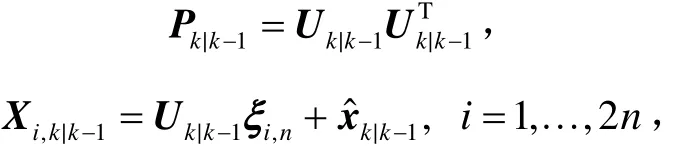
ξi,n表示n×2n维容积点集的第i列向量。

将式(68)(73)代入定理2中对应各项，即可实现对k时刻的系统状态xk的估计。

4 仿真分析

本论文采用非线性滤波领域中常用的测试模型—单变量非静态增长模型(UNGM)[30-31]，来验证所提出的CKF-RDCN滤波算法的有效性。该测试模型含有三角函数以及平方函数等强非线性项，其具体形式如下：

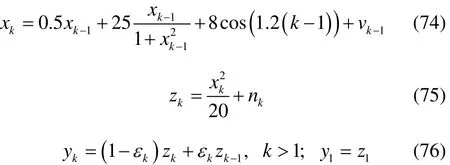
式中：vk-1和nk是均值为零，方差分别为Qk-1=4和 Rk=12的相关高斯白噪声，其噪声相关系数Sk=0.1, 0.2,…,0.7；εk（k＞1）是Bernoulli分布下的互不相关的随机序列，其发生概率pk=0.1,0.2,…,0.9。设仿真初始值x0=-0.7，方差初始值P=1，仿真时长T=200。此外，以状态估计的均方根误差(RMSE)，来比较EKF、CKF以及CKF-RDCN等滤波算法的估计性能。RMSE定义如下：

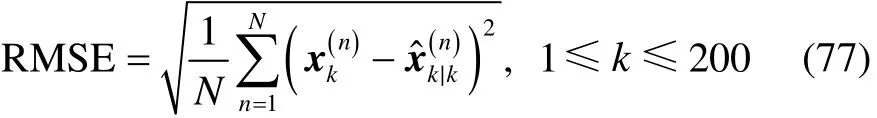
图1图3对不同噪声相关和观测时滞情况下滤波算法的估计性能进行了比较。图1对比了时滞概率相同而噪声相关系数不同情况下的估计结果。从图1可知，由于测试模型本身的强非线性，导致了EKF的估计结果相对于CKF和CKF-RDCN是较差的，且在初始过程等阶段出现了幅值较大的尖峰。估计结果的较大波动性，必然会给实际系统的使用造成损害。CKF由于在处理非线性情况的优势，其估计结果要好于EKF，然而由于噪声相关和观测时滞情况的引入，其在k=70和k=180等时刻同样出现了幅值较大的尖峰。对比可知，图1(a)和图1(b)中CKF-RDCN的数值稳定性和估计误差均优于CKF滤波算法，且CKFRDCN噪声相关系数较大时的数值稳定性要好于其较小时刻。图2展示了噪声相关系数相同，而时滞概率不同情况下的估计结果。与图1中的情况类似，由于测试模型本身的非线性，导致EKF的估计结果在初始阶段以及k=50和k=100等时刻出现了幅值较大的尖峰。对比估计结果可知：当pk=0.2时，CKF-RDCN的估计结果虽然要好于CKF滤波算法，但二者性能之间的差距较小；而当pk取值增大到0.8时，CKF在k=70和k=160等时刻出现尖峰，数值稳定性下降，滤波估计结果差于CKF-RDCN滤波算法。图3对比了不同噪声相关系数和不同观测时滞情况下的滤波器估计结果，分析可知，不同噪声相关系数和不同观测时滞情况下，所提出的CKF-RDCN滤波算法其数值稳定性和误差估计结果均优于EKF滤波算法和CKF滤波算法。此外，从图1和图2的估计结果可知，噪声相关系数或观测时滞概率中某一项的增大会导致EKF和CKF滤波算法性能的下降，然而图3(a)和图3(b)中EKF滤波算法和CKF滤波算法取得估计性能最差的情况并不是在噪声相关系数与观测时滞概率同为最大的时刻，这说明二者对滤波器性能的影响不是简单的线性关系。

图1 Sk=0.2和Sk=0.7情况下的EKF、CKF以及CKF-RDCN性能比较Fig.1 Comparison on EKF, CKF and CKF-RDCN with Sk=0.2 and Sk=0.7

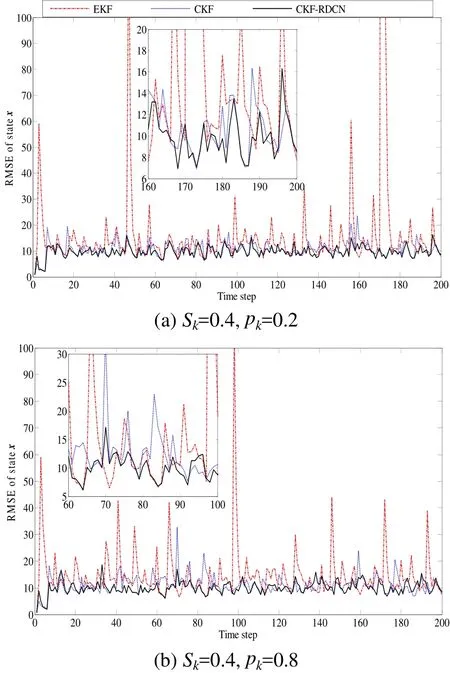
图2 pk=0.2和pk=0.8情况下的EKF、CKF以及CKF-RDCN性能比较Fig.2 Comparison on EKF, CKF and CKF-RDCN with pk=0.2 and pk=0.8

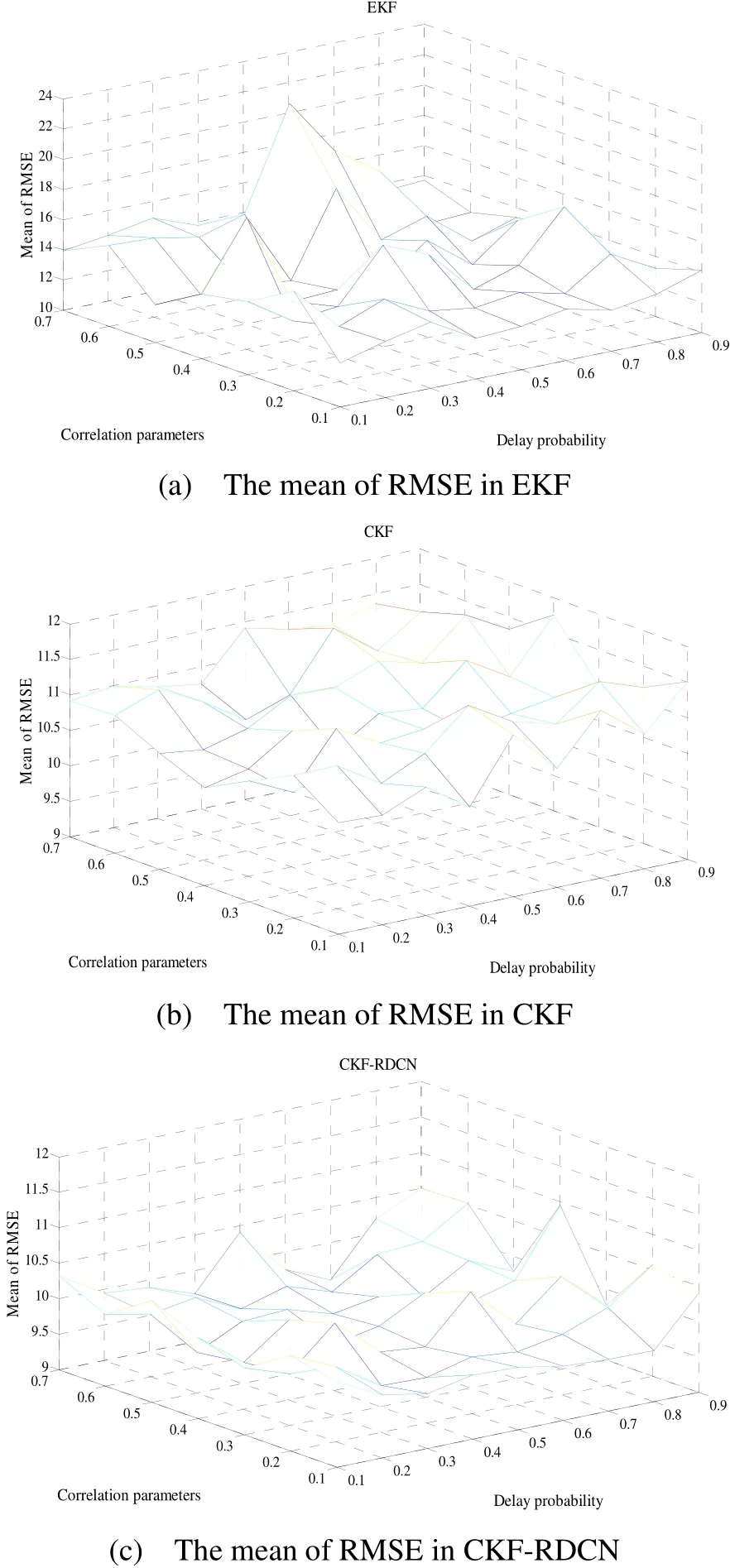
图3 Sk= 0.1, 0.2, ...,0.7和pk= 0.1, 0.2, ...,0.9情况下的EKF、CKF以及CKF-RDCN性能比较Fig.3 Comparison on EKF, CKF and CKF-RDCN with Sk= 0.1, 0.2, ...,0.7 and pk= 0.1, 0.2, ...,0.9

5 结论

首先，考虑了具有随机时滞和异步相关噪声系统的状态估计问题，针对经典GF算法无法解决随机时滞，以及要求过程噪声和量测噪声互不相关的假设限制，提出了一种改进的GF算法。分析可知，所提出的改进GF算法是对经典GF算法的拓展，经典GF算法是改进GF算法在系统无随机时滞、无异步相关噪声情况下的特例。其次，考虑到在改进GF算法的设计过程中，采用将量测噪声作为系统状态增量的方式可能导致滤波算法数值稳定性下降的问题，给出了其在三阶球径容积法则下的实现形式，以适应高维状态估计的需要。最后，通过仿真分析对比EKF算法、CKF算法以及CKF-RDCN算法在随机时滞和相关噪声情况下的状态估计性能可知，CKF-RDCN算法具有最优的性能表现。此外，同随机时滞和噪声相关等因素相比而言，滤波算法对系统非线性问题的解决是影响估计精度和数值稳定性最主要的因素，然而，对于精度要求较高的系统，在设计其状态估计算法时仍需考虑对随机时滞和噪声相关等因素的解决，以期提供状态估计结果的精度和数值稳定性。

References)

[1] Ghadiok V, Goldin J, Geller D. Gyro-aided vision-based relative pose estimation for autonomous rendezvous and docking[C]//36th Annual AAS Rocky Mountain Section Guidance and Control Conference. Colorado, United States, 2013: 713-728.

[2] Nemra A, Aouf N. Robust INS/GPS sensor fusion for UAV localization using SDRE nonlinear filtering[J]. IEEE Sensors Journal, 2010, 10(4): 789-798.

[3] Ieng S H, Posch C, Benosman R. Asynchronous neuromorphic event-driven image filtering[J]. Proceedings of the IEEE, 2014, 102(10): 1485-1499.

[4] Date P, Ponomareva K. Linear and non-linear filtering in mathematical finance: a review[J]. IMA Journal Management Mathematics, 2011, 22(3): 195-211.

[5] Crassidis J L, Junkins J L. Optimal estimation of dynamic systems[M]. Boca Raton: Chapman & Hall/ CRC, 2004: 285-292.

[6] Joglekar A N. A Technique to improve the performance of a nonlinear filter with an application to satellite-aided aircraft navigation[C]//13th IEEE Conference on Symposium on Adaptive Processes. 1974: 159-164.

[7] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceeding of the IEEE, 2004, 92(3): 401-422.

[8] Ito K, Xiong K. Gaussian filters for nonlinear filtering problems[J]. IEEE Trans. on Automatic Control, 2000, 45(5): 910-927.

[9] Nrgaard M, Poulsen N K, Ravn O. New developments in state estimation for nonlinear systems[J]. Automatica, 2000, 36(11): 1627-1638.

[10] Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Trans. on Automatic Control. 2009, 54(6): 1254-1269.

[11] Jia B, Xin M, Cheng Y. Sparse-grid quadrature nonlinear filtering[J]. Automatica, 2012, 48(2): 327-341.

[12] Jung K, Kim J, Kim J, et al. Positioning accuracy improvement of laser navigation using UKF and FIS[J]. Robotics and Autonomous Systems, 2014, 62(9): 1241-1247.

[13] 胡高歌, 高社生, 赵岩. 一种新的自适应UKF算法及其在组合导航中的应用[J]. 中国惯性技术学报, 2014, 22(3): 357-361, 367. Hu G G, Gao S S, Zhao Y. Novel adaptive UKF and its application in integrated navigation[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 357-361, 367.

[14] Jwo D J, Hsieh M Y, Lai S Y. GPS navigation processing using the quaternion-based divided difference filter[J]. GPS Solutions, 2010, 14(3): 217-228.

[15] 孙枫, 唐李军. 基于Cubature Kalman Filter的INS/ GPS 组合导航滤波算法[J]. 控制与决策, 2012, 27(7): 1032-1036. Sun F, Tang L J. INS/GPS integrated navigation filter algorithm based on cubature Kalman filter[J]. Control and Decision, 2012, 27(7): 1032-1036.

[16] Jia B, Xin M. Vision-based spacecraft relative navigation using sparse-grid quadrature filter[J]. IEEE Trans. on Control Systems Technology, 2013, 21(5): 1595-1606.

[17]Kim D M, Suk J. GPS output signal processing considering both correlated/white measurement noise for optimal navigation filtering[J]. International Journal of Aeronautical and Space Sciences, 2012, 13(4): 499-506.

[18]崔玉平, 曾威, 王文辉, 等. 时间相关噪声条件下的捷联惯导/星敏感器组合导航方法[J]. 中国惯性技术学报, 2012, 19(6): 696-700. Cui Y P, Zeng W, Wang W H, et al. SINS/Star sensor integrated navigation method in the presence of time correlated noises[J]. Journal of Chinese Inertial Technology, 2012, 19(6): 696-700.

[19]Asadi E, Bottasso C L. Delayed fusion for real-time vision-aided inertial navigation[J]. Journal of Real-Time Image Processing. 2013: 1-14. (Article in Press)

[20]Bar-Shalom Y, Li X R, Kirubarajan T. Estimation with applications to tracking and navigation[M]. New York: John Wiley & Sons, 2001: 324-327.

[21]Chang G B. Marginal unscented Kalman filter for cross-correlated process and observation noise at the same epoch[J]. IET Radar, Sonar and Navigation, 2014, 8(1): 54-64.

[22]王小旭, 赵琳, 夏全喜, 等. 噪声相关条件下Unscented卡尔曼滤波器设计[J]. 控制理论与应用, 2010, 27(10): 1362-1368. Wang X X, Zhao L, Xia Q X, et al. Design of unscented Kalman filter with correlative noises[J]. Control Theory & Applications, 2010, 27(10): 1362-1368.

[23]徐小良, 汤显峰, 葛泉波, 等. 基于量化新息的容积粒子滤波融合目标跟踪算法[J]. 自动化学报, 2014, 40(9): 1867-1874. Xu X L, Tang X F, Ge Q B, et al. Target tracking algorithm based on cubature particle filtering fusion with quantized innovation[J]. Acta Automatica Sinica, 2014, 40(9): 1867-1874.

[24]Wang X X, Liang Y, Pan Q, et al. A Gaussian approximation recursive filter for nonlinear systems with correlated noises[J]. Automatica, 2012, 48(9): 2290-2297.

[25]Hermoso-Carazo A, Linares-Pérez J. Extended and unscented filtering algorithms using one-step randomly delayed observations[J]. Applied Mathematics and Computation, 2007, 190(2): 1375-1393.

[26]Hermoso-Carazo A, Linares-Pérez J. Unscented filtering algorithm using two-step randomly delayed observations in nonlinear systems[J]. Applied Mathematical Modelling, 2009, 33(9): 3705-3717.

[27]Wang X X, Liang Y, Pan Q, et al. Design and implementation of Gaussian filter for nonlinear system with randomly delayed measurements and correlated noises[J]. Applied Mathematics and Computation, 2014, 232: 1011-1024.

[28]Ge Q B, Xu D X, Wen C L, Cubature information filters with correlated noises and their applications in decentralized fusion[J]. Signal Processing, 2014, 94(1): 434-444.

[29]Wang X X, Liang Y, Pan Q, et al. Gaussian filter for nonlinear systems with one-step randomly delayed measurements[J]. Automatica, 2013, 49(4): 976-986.

[30]Kim S, Park J S. Sequential Monte Carlo filters for abruptly changing state estimation[J]. Probabilistic Engineering Mechanics, 2011, 26(2): 194-201.

[31]Kim D Y, Jeon M. Square root receding horizon information filters for nonlinear dynamics system models[J]. IEEE Trans. on Automatic Control, 2013, 58(5): 1284-1289.

Improved Gaussian filter algorithm for nonlinear system with random delay and asynchronously correlated noises

YU Han1, SONG Shen-min1, WANG Shuo1, LI Peng2
(1. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China; 2. College of Information Engineering, Xiangtan University, Xiangtan 411100, China)

To solve the problem of states estimation with randomly delayed measurements and correlated noises, an improved Gaussian filter(GF) is proposed, and its implementation in high-dimensional system is given, which is by cubature Kalman filters with randomly delay and correlated noises(CKF-RDCN). Firstly, an independent random sequence of Bernoulli distribution is used to describe the phenomena of possible random delay in observation measurements, and the measurement noises are taken as state vectors to estimate the probability density function of the delayed observation. Secondly, the first-order of Stirling’s interpolation is employed to calculate the multi-dimensional integrals with random variables caused by correlated noises. Finally, the proposed CKF-RDCN is deduced from the third-order spherical-radial rule. While the classical GF can be taken as a special form of the proposed novel GF, a general algorithm frame of nonlinear filter can have different implementations based on various approximate methods of probability density functions. Simulation results demonstrate that the CKF-RDCN is more accurate and stable than the extended Kalman filter and CKF in state estimation when with randomly delayed measurements and correlated noises.

nonlinear filter; Gaussian filter; random delay; correlated noises; cubature Kalman filter

V448.133

1005-6734(2015)02-0238-10

10.13695/j.cnki.12-1222/o3.2015.02.018

2014-11-29；

2015-03-14

国家自然科学基金（61174037）

于浛（1985—），男，博士研究生，主要研究方向为航天器姿态确定、非线性滤波以及视觉/惯性组合导航。E-mail：yuhanihit@163.com

联系人：宋申民（1968—），男，教授，主要研究方向为飞行器导航、制导与控制以及非线性滤波算法。