Improved fast backtracking alignment approach for strapdown inertial navigation system

HE Hong-yang, XU Jiang-ning, LI Jing-shu, LI Feng, ZHA Feng

(Department of Navigation, Navy University of Engineering, Wuhan 430033, China)

Improved fast backtracking alignment approach for strapdown inertial navigation system

HE Hong-yang, XU Jiang-ning, LI Jing-shu, LI Feng, ZHA Feng

(Department of Navigation, Navy University of Engineering, Wuhan 430033, China)

Rapidity is vital important for initial alignment of strapdown inertial navigation system (SINS). Backtracking algorithm can effectively reduce the alignment time by repeatedly using the recorded measurements of gyros and accelerometers. In order to further improve the rapidity, a fast backtracking alignment approach (FBA) was designed. An optimization-based alignment approach was employed during coarse alignment stage to provide more accurate initial attitude for the fine alignment of backtracking gyrocompass, so as to improve the rapidity of the gyrocompass loop’s convergence. The fundamental principle of backtracking algorithm was analyzed, and the implementation process of the FBA was designed. Experiment results show that the proposed algorithm can greatly reduce the execution times of backtracking and the data volume in alignment, further improving the rapidity of alignment.

strapdown INS; initial alignment; backtracking alignment approach; rapid alignment

The alignment of strapdown inertial navigation system is by using the measurements from the accelerometers and gyroscopes to determine the orientation of the body frame with respect to a reference frame[1-5]. The Alignment process is divided into two parts: coarse alignment and fine alignment. Coarse alignment is an analytical alignment which suffers from a lack of precision as measurement errors and other noise sources are not considered. It does, however, estimate the attitude and heading accurately enough to justify the small angle approximations made in the error model. Nowadays, there are two main methods of self-alignment: Kalman filtering fine alignment with the result from the analytic coarse alignment; and gyrocompass alignment techniques. The contradiction between rapidity and high-precision exists in both of the above approaches. In order to solve this problem, a backtracking gyrocompass alignment approach is proposed[6-9], in which the measurements ofgyros and accelerometers within a short time are recorded for repeated calculation, so as to minimize the alignment time. However, the coarse alignment error of gyrocompass alignment is relatively large. So the gyrocompass loop converges slowly. The volume of the recorded data and execution times of backtracking calculation need to be large enough to achieve high- precision alignment. An optimization-based alignment approach is proposed in [10] and [11]. It is considered to be a coarse alignment because the process only determines the attitude matrix without estimating the errors of the sensor, but it possesses the advantages of rapidity and can guarantee quite a high accuracy[12]. Another advantage of this approach is that the three attitude angles gradually converge at the same time. However, there exists slowly climbing trends in level angles as well as the biased yaw in the algorithm, which are owed to the existence of gyro/accelerometer biases that has not been taken into account.

This paper proposes a fast backtracking alignment approach based on the optimization-based coarse alignment and backtracking gyrocompass alignment. The coarse alignment based on optimization-based alignment algorithm is carried out by using a small amount of recorded measurements of gyros and accelerometers. Within this stage, three attitude angles converge rapidly to the accurate values. Then, an accurate alignment is achieved based on the backtracking gyrocompass approach. Compared with traditional alignment approaches, the proposed algorithm can greatly reduce the alignment time. Compared with the backtracking gyrocompass alignment, the proposed algorithm can effectively reduce the execution times of backtracking and the volume of the data that has to be recorded for backtracking.

1 Backtracking navigation algorithm

Denote by n the local level navigation frame, an orthogonal reference frame aligned with north–east–down (NED) geodetic axes; by b the SINS body frame, an orthogonal reference frame aligned within the IMU axes; by e the Earth frame, an Earth-centered Earthfixed (ECEF) orthogonal reference frame; by i the chosen inertial frame.

The navigation (attitude, velocity and position) rate equations in the n-frame are respectively known as:

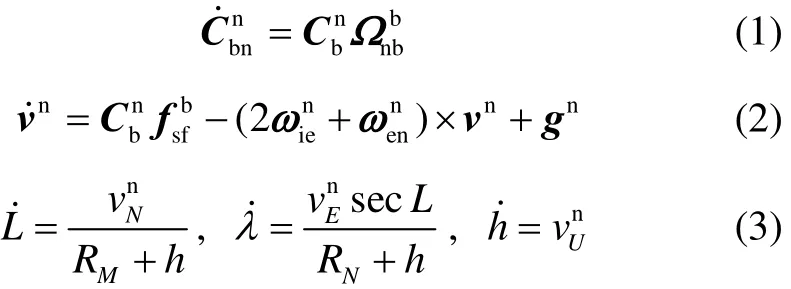
Where,

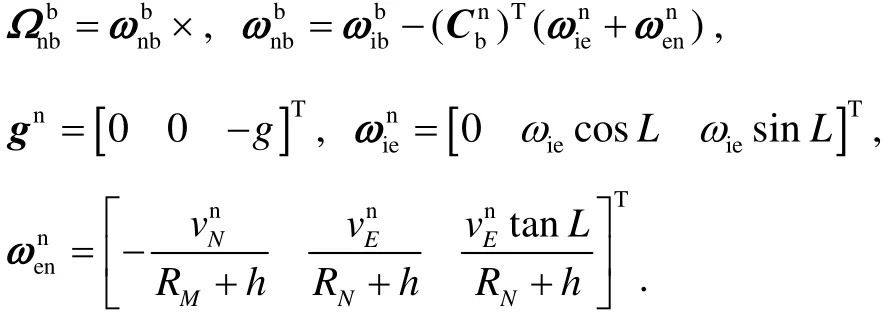
Thus, the attitude, velocity and position updating can be presented respectively as follows:

Attitude updating:

Velocity updating:

Position updating:

Where,

Tsdenotes the SINS sampling period.

Assume that SINS navigates from point A to point B and the measurements of gyros and accelerometers are recorded. In order to navigate from point B to point A using the recorded data, the backtracking updating process can be rearranged and presented as follows:

Attitude updating:

Velocity updating:

Position updating:

Where,

Denote:

Rearrange equation (7)(9).

Attitude updating:

Velocity updating:

Position updating:

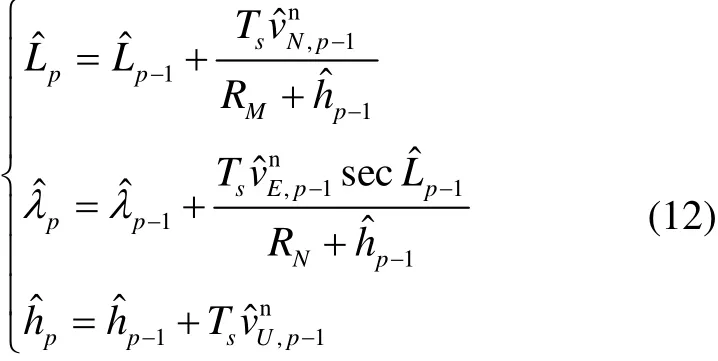
Where,

Through the above analysis, it can be concluded that, by negating the measurements of gyros and← the Earth rotation rate, setting the initial values asand reversing the recorded measurements of gyros and accelerometers, navigating from B point (at tm) to A point ( at t0) can be achieved.

2 Improved fast backtracking alignment

The coarse alignment error of gyrocompass alignment is relatively large. So the gyrocompass loop converges slowly. The volume of the recorded data and execution times of backtracking calculation need to be large enough to achieve high-precision alignment. In order to improve the rapidity and precision of the coarse alignment, an optimized-based alignment algorithm is employed, whose main idea can be described as follows.

The navigation (attitude, velocity and position) rate equations are presented in equation (1)(3). Suppose the alignment process starts from t=0. Given the measured velocity vnand position p over the time interval with the purpose to determine the attitude matrix, which at any time satisfies

So the optimization-based alignment focuses on determining. Substituting (13) into (2) yields

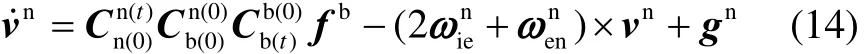
Integrating (15) on both sides:

The velocity integration formula can be presented as

Where,

Note the four elements unit quaternion q=[sηT]Tis used to encode the initial body attitude matrix, where s is the scalar part, and η is the vector part. The relationship between these two rotation parameters is

Define the quaternion multiplication matrices by

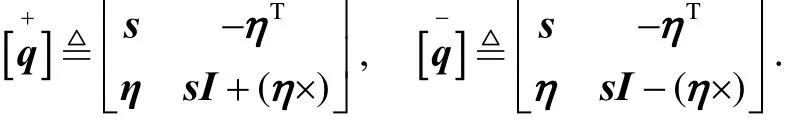
Then (16) is equivalent to

And the determination of the attitude quaternion can be posed as a constrained optimization, subject to qTq=1. Where the 4×4 real symmetric matrix

It can be proved that the optimal quaternion is exactly the normalized eigenvector of K belonging to the smallest eigenvalue. Then, the attitude matrixat any time can be determined by using the(0).

Comparing with the traditional analytical and inertial frame coarse alignment, the optimization-based alignment uses more observations and possesses the advantages of rapidity and can guarantee quite a high accuracy. The optimization-based alignment is employed as the coarse alignment approach in fast backtracking alignment algorithm proposed in this paper. As the precision of the coarse alignment is very high, the execution times of backtracking and the volume of recorded data need for gyrocompass backtracking alignment can be reduced, thus the rapidity of alignment will be further improved and the computational cost of navigation computer is decreased greatly.

3 Experimental results

This section reports our experimental results by examining a real SINS consisting of three fibre optical gyroscopes (FOG) with drift rate 0.01 (°)/s and three quartz accelerometers with bias 5×10-4m/s2at output rate 10 Hz. The FOG SINS was installed on a doubleaxis turntable, as shown in Fig.2.

In order to evaluate the accuracy of alignment, we needed a criterion for comparison. Thus we ensured that the turntable had a highly accurate level through a level meter and an exact heading through an optical theodolite.

Fig.1 IMU of FOG strapdown INS

Fig.2 IMU on turntable

The parameters were as follows: attitude of IMU is [pitch, roll, yaw] =[ 0°, 0°, 36.8°], the sampling frequency is 10 Hz. The gyro and accelerometer measurements are collected for 300 s. Experiment with the proposed fast backtracking gyrocompass alignment (FBA) algorithm was carried out using the data from 0 s to 50 s. Two experiments with the backtracking gyrocompass alignment (BA) algorithm were carried out using the data from 0 s to 50 s and 0 s to 100 s respectively.

Fig.3 to Fig.6 compare the attitudes estimated by FBA algorithm and the BA algorithm. Fig.3 shows the roll angle. Fig.4 shows the pitch angle. Fig.5 and Fig.6 show the yaw angle. It is clearly shown that, when the data used for alignment last 50 s, the estimates of the Euler angles by FBA converged much faster that by BA. It means that the proposed algorithm can greatly decrease the execution times of backtracking and greatly decrease the computational cost. Even when the data used for BA increase to 100 s, the estimates of the Euler angles by FBA (using 50 s data) converged faster than that with BA (using 100 s data). It means that the proposed algorithm can effectively reduce the volume of the data that has to be recorded for alignment, thus therapidity of alignment will be further improved.

Fig.3 Estimates of roll

Fig.4 Estimates of pitch

Fig.5 Estimates of yaw

Fig.6 Partial enlarged yaw

4 Conclusions

In many applications, it is essential to achieve an accurate alignment for an inertial navigation system within a very short period of time. In this paper, a fast backtracking alignment approach (FBA) has been developed based on optimization-based coarse alignment and backtracking gyrocompass fine alignment for strapdown inertial navigation system. The backtracking algorithm is derived mathematically and the implementation process of FBA is designed. The effectiveness of the method has been verified by the measured data. Experimental results show that, comparing with the backtracking gyrocompass alignment proposed in [6], the proposed algorithm in this paper can greatly decrease the execution times of backtracking, so the computational cost will be decreased. And FBA can effectively reduce the volume of data that has to be recorded to guarantee the alignment precision, thus the rapidity of alignment will be further improved.

Reference:

[1] Titterton H D, Weston L J. Strapdown inertial navigation technology[M]. 2nded. The Institution of Electrical Engineers, 2004.

[2] Silson P G. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE transaction on instrument and measurement, 2011, 60: 1930-1941.

[3] QIN Y Y, Mei C B, Bai L. Error and calculation problem analysis of coarse alignment method with inertial frame for SINS[J]. Journal of Chinese Inertial Technology, 2010, 18(6): 648-652.

[4] Qin Y Y, Yan G M, Gu D Q, Zheng J B. A clever way of SINS coarse alignment despite rocking ship[J]. Journal of Northwestern Polytechnical University, 2005, 23(5): 681-684.

[5] Sun W, Sun F, Lin Y. Research on rapid initial alignment of SINS with swaying motion[J]. Journal of System Simulation, 2013, 25(3): 681-684.

[6] Yan G M. On SINS in-movement initial alignment and some other problems[D]. Xi’an: Northwestern Polytechnical University, 2008.

[7] Li W L, Tang K H, Lu L Q, Wu Y L. Optimization-based INS in-motion alignment approach for underwater vehicles [J]. Optic, 2013, 124: 4581-4585.

[8] Li W L, Wu W Q, Wang J L, Lu L Q A. Fast SINS initial alignment scheme for underwater vehicle applications[J]. The Journal of Navigation, 2013, 66: 181-198.

[9] Qin F J, Li A, Xu J N. Improved fast alignment method of strapdown INS using bidirectional processes and denoising[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 453-458.

[10] Wu M P, Wu Y X, Hu X P, Hu D W. Optimization-based alignment for inertial navigation systems: Theory and algorithm[J]. Aerospace Science and Technology, 2011, 15: 1-17.

[11] Wu Y X, Pan X F. Velocity/position integration formula Part I: Application to in-flight coarse alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49: 1006-1023.

[12] Li J S, Xu J N, Chang L B, Zha F. An improved optimal method for initial alignment[J]. The Journal of Navigation, 2014, 67: 727-736.

捷联惯导系统改进回溯快速对准方法

何泓洋，许江宁，李京书，李 峰，查 峰
（海军工程大学 导航工程系，湖北 武汉 430033）

快速性是捷联惯导系统初始对准的一项重要指标。回溯算法通过存储一段时间的陀螺仪和加速度计的数据，并反复加以利用的方式，有效缩短了对准的时间。为了进一步提高初始对准的快速性，设计了一种快速回溯对准方法（FBA）。优化对准方法被用于算法的粗对准阶段，为回溯罗经法精对准提供较为准确的初始姿态，进而提高罗经回路的收敛速度。分析了回溯算法的基本原理，设计了快速回溯对准算法的实施过程。实验结果表明，提出的算法能够降低回溯次数，大大减少对准所需的数据量，使得对准的快速性进一步提高。

捷联惯性导航系统；初始对准；回溯对准法；快速对准

U666.1

A

1005-6734(2015)02-0179-05

2014-12-09；

2015-03-28

国家重大科学仪器开发专项（2011YQ12004502）；国家自然科学基金（41404002）；海军工程大学青年基金（HGDQNEQJJ13011）

何泓洋（1990—），男，博士研究生，从事惯性技术研究。E-mail：xgdhehongyang@163.com

10.13695/j.cnki.12-1222/o3.2015.02.008

联 系 人：许江宁（1964—），男，教授，博士生导师。E-mail：xujiangning2005@163.com