基于强跟踪滤波的车载行进间对准
2015-06-05赵小明郭永刚王晓亮周凌峰
赵小明,赵 帅,郭永刚,王晓亮,周凌峰,王 强
(1. 天津航海仪器研究所,天津 300131;2. 哈尔滨工程大学 自动化学院,哈尔滨 150001;3. 北京总装北京军事代表局驻天津地区军事代表室,天津 300131)
基于强跟踪滤波的车载行进间对准
赵小明1,赵 帅1,郭永刚1,王晓亮1,周凌峰2,王 强3
(1. 天津航海仪器研究所,天津 300131;2. 哈尔滨工程大学 自动化学院,哈尔滨 150001;3. 北京总装北京军事代表局驻天津地区军事代表室,天津 300131)
针对车载行进间对准过程中存在复杂路面和未知干扰的情况,提出基于强跟踪滤波的里程计辅助车载捷联惯导行进间对准方法。采用多重渐消因子的强跟踪滤波器进行车载行进间精对准。多重渐消因子的强跟踪滤波器利用卡尔曼滤波取得最佳增益时残差序列互不相关的性质,在线自适应地调整渐消因子,对未知干扰有较强的鲁棒性。建立行进间对准的状态方程与观测方程,针对三种不同路况进行了8次跑车行进间对准试验。试验结果表明:强跟踪滤波能适应恶劣复杂路况;精对准后航向误差(1σ)≤3.6′,满足指标要求。
捷联惯导系统;行进间对准;卡尔曼滤波;多渐消因子强跟踪滤波
随着对车载系统的快速反应能力、恶劣环境生存能力的要求越来越高,具备行进间对准能力的车载捷联惯导系统逐渐成为研究热点。
行进间对准在行车过程中实现对惯性导航系统的补偿和修正,通常需要利用外部设备(GPS或里程计)提供载体运动信息。GPS能直接提供载体位置和速度,对准速度快、精度高,但是其信号易受遮挡导致关键时刻可利用性低[1];相比较,里程计辅助行进间对准具有全自主性,但对数据处理技术有较高要求。国内严恭敏、肖烜[2]等学者对里程计辅助载车行进间对准进行了相关研究。
里程计辅助下的捷联惯导行进间对准包括粗对准和精对准。精对准过程常采用卡尔曼滤波算法,然而实际对准过程中,由于存在复杂路面和未知干扰的情况,系统噪声统计特性经常发生变化,导致卡尔曼滤波性能下降,严重时甚至发散。本文提出将强跟踪滤波引入行进间对准,以克服标准卡尔曼滤波鲁棒性差的不足。跑车试验表明,强跟踪滤波行进间对准在复杂路面情况下有较好的对准精度。
1 多重渐消因子强跟踪滤波
多重渐消因子强跟踪滤波器是在标准卡尔曼滤波技术上改进的一种滤波算法。标准卡尔曼滤波递推方程为:
状态一步预测方程:

一步预测均方误差方程:
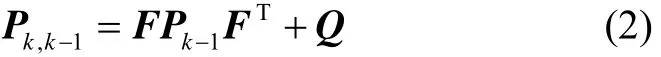
滤波增益方程:
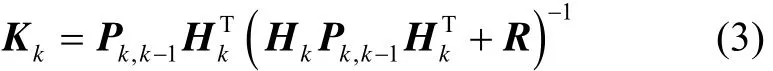
状态估计方程:
估计均方误差:
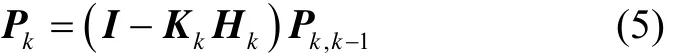
多重渐消因子强跟踪滤波算法是在式(2)中引入一个对角矩阵渐消因子,使得不同时刻的残差序列处处保持正交:

式中:F为状态向量X为从tk-1时刻转移到tk时刻的转移矩阵;Dk+1为多重渐消因子的对角矩阵,可由下面方法确定:

式中:αi≥1,i=1,2,…,n 为由先验知识预先确定的系数。可以增大易于突变状态分量相应的αi,若无系统先验知识时,取αi=1。式(8)中,
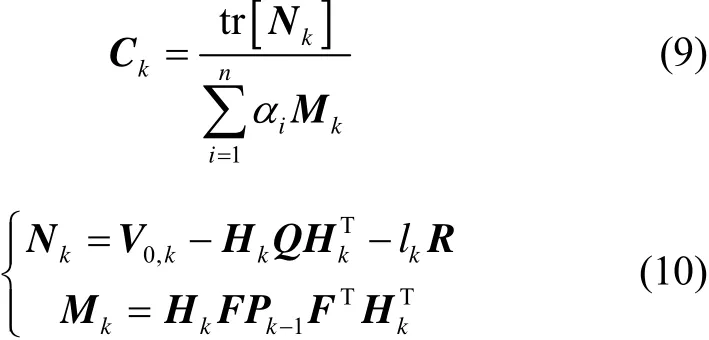
式中:tr[·]为求迹算子;Q为系统噪声方差阵;R为量测噪声方差阵;Pk-1为tk-1时刻最优滤波值误差协方差阵;lk≥1为弱化因子;V0,k为均方误差值;Hk为tk时刻量测矢量Zk与状态向量X间的量测系数矩阵。
多渐消因子的卡尔曼滤波器针对各数据通道以不同的速率进行渐消,可以更好地调整增益矩阵,即使当系统达到稳态时,也能自适应地调整增益矩阵,从而达到增强对模型失配和系统扰动的鲁棒性,得到更加精确和稳定的估计结果[3-5]。
2 强跟踪行进间对准设计
车载行进间对准分为粗对准和精对准两个阶段。
在粗对准阶段,参照文献[6],建立载体惯性凝固坐标系,将姿态阵分解为三个矩阵求解,根据陀螺和加速度计的输出直接解算出姿态阵:

在精对准阶段:惯导系统提供车辆的姿态信息;里程计提供载体运动信息,建立失准角误差模型,运用滤波器估计出车辆的姿态失准角、陀螺常值漂移和加速度计零偏,根据滤波得到的车辆姿态失准角修正输出的车辆姿态,根据陀螺常值漂移与加速度计零偏估计值修正惯性敏感器件误差初始值。重复此过程,直至滤波估计量收敛,完成行进间对准。
2.1 坐标系说明
n系:导航坐标系,采用当地地理坐标系(方向为东北天);
b系:车体坐标系,方向为右前上;
b′系:在惯导系统安装处的载体系,它与车体固联,与b系存在安装误差角;
in0系:导航系凝固而成的惯性坐标系;
ib0系:载体系凝固而成的惯性坐标系。
2.2 状态模型建立
假设导航计算坐标系和当地地理坐标系间的失准角误差为小角度误差矢量。光纤捷联惯导与里程计组成组合导航系统。车载环境下,主要是由于安装、使用环境等因素造成的误差,包括由惯导系统在载体上的安装偏差角产生的航向安装误差角δψα和俯仰安装误差角δθα以及里程计标度因子误差δKD。其中,里程计标度因数误差与环境温度、路面状况等因素有关[7]。
设里程计在载体系下的输出矢量为:
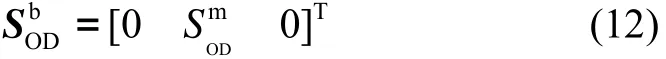
考虑到惯导在载体上的安装误差和标度因数误差,里程计的路程输出在b′系下的矢量为:
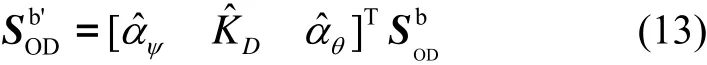
K为里程计标度因数修正量。上述修正量的误差记为δψα、δθα和δKD,实际中通常假设上述误差量为常值,从而安装误差及里程计标度误差模型为:

导航系下捷联惯性导航系统的误差模型为:
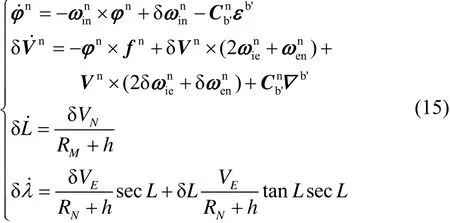
结合惯导安装误差及里程计标度误差,选取姿态角误差、速度误差、位置误差、陀螺常值漂移、加速度计零偏和安装误差及里程计标度来构成状态变量X:
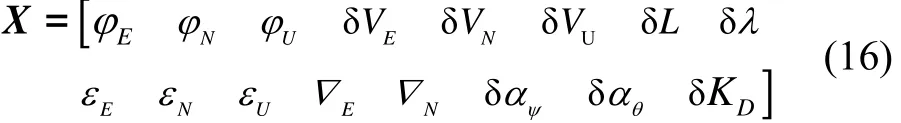
2.3 量测方程建立
以惯导解算位置增量和里程计位置增量之差作为强跟踪滤波器的观测量。惯导系统的位移增量为:

考虑惯导在载体系下的安装误差,则有b系和b′系之间的转换关系。
里程计的位移量在导航坐标系上的投影为:

实际里程计位移输出在n系下分量为:

将式(19)展开,并忽略关于δψα、δθα和δKD的高阶小量得:
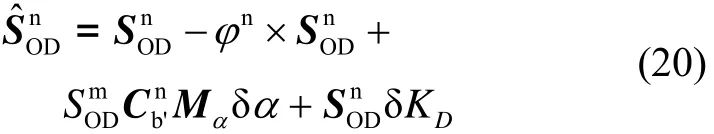
式中:
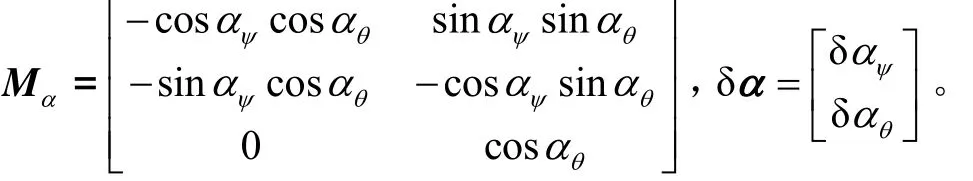
里程计位移增量在n系下的矢量误差方程:
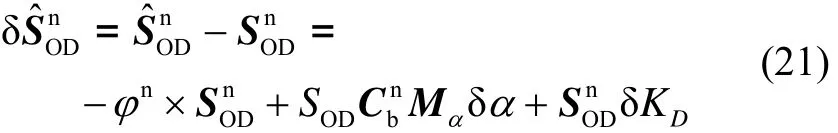
组合导航系统的观测方程:

根据观测方程建立相应的观测矩阵Hk。
2.4 强跟踪滤波估计过程
根据系统误差模型和观测量的建立,建立系统的的状态方程和量测方程:

式中:X表示系统状态;Z表示观测向量;F和H分别为系统的状态函数和量测函数,W和V为互不相关的零均值高斯白噪声,
多渐消因子强跟踪滤波过程:
① 状态预测:

② 计算带多重次优渐消因子的对角矩阵,其中,

式中,0≤ρ≤1为遗忘因子。
③ 用式(6)计算预测状态协方差阵。
④ 计算增益矩阵:
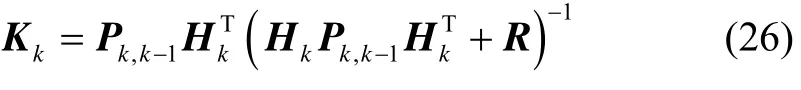
⑤ 计算t时刻状态估计协方差阵和状态估计值:

根据以上步骤,编辑多重渐消因子的强跟踪滤波导航解算程序。
3 试验验证
采用的光纤陀螺零偏稳定性为0.01 (°)/h,加速度计零偏稳定性为50 μg,捷联惯导采样周期为0.01 s。行进间粗对准时间50 s,精对准时间10 min。为继续观察收敛情况,将试验时间延长至800 s。共进行8组跑车试验,行车路况包括三种:① 一般路况(第1、6组);② 上下坡路况(第2、3、5组);③ 沙土路(第4、7、8组)。试验过程中对载车加减速过程及行驶速度不做特殊要求。
图1、图2和图3分别为精对准过程中航向角误差的收敛曲线。由于俯仰角和横滚角误差对准收敛速度快,而航向角误差收敛速度慢,因此本文通过研究航向角误差的对准精度和对准时间来说明提出的滤波算法的有效性。从图1~3中可以看出,第600 s时误差曲线基本达到平稳。取每种工况下第600 s时的航向角误差列于表1。从表1知,第600 s时使用强跟踪滤波器对准的航向角误差为3.58′(1σ),满足行进间对准的精度要求,表明当存在复杂路面和外界扰动时,所设计的强跟踪滤波方法能够较好地估计载车姿态失准角,实现行进间对准。
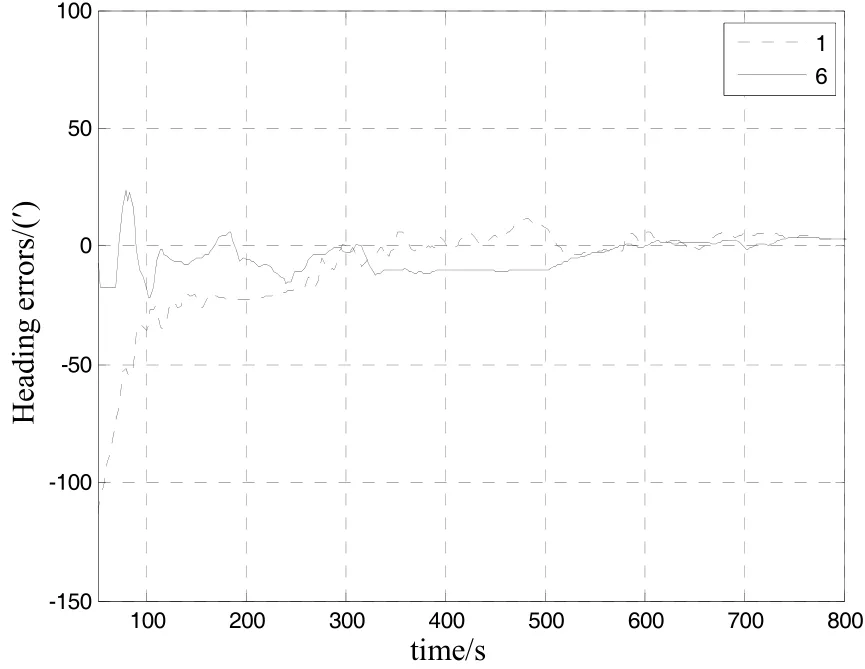
图1 第1、6组试验航向角误差曲线Fig.1 Experiments 1 and 6 for heading angle
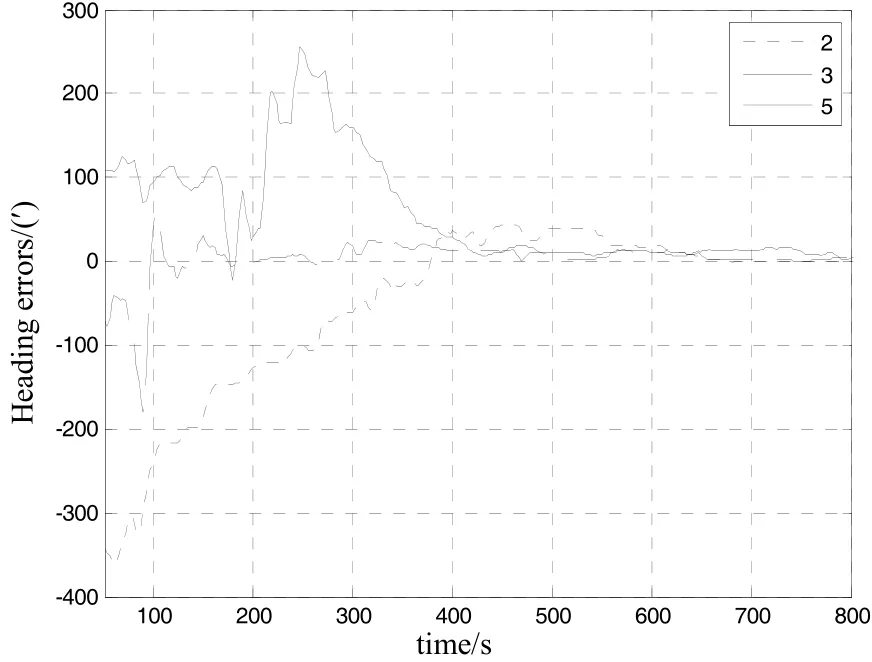
图2 第2、3、5组试验航向角误差曲线Fig.2 Experiments 2, 3 and 5 for heading angle

图3 第4、7、8组试验航向角误差曲线Fig.3 Experiments 4, 7, and 8 for heading angle

表1 对准600 s时各组航向角误差Tab. 1 Errors of heading angle at 600 s
4 结 论
本文提出将强跟踪滤波算法应用于车载行进间对准,通过分析多重渐消因子强跟踪滤波的原理,建立车载行进间对准的状态模型和量测模型,设计出相应的强跟踪滤波器。对不同路况进行了8组跑车试验,结果表明,强跟踪滤波算法适用于包含复杂路况和外界干扰的车载行进间对准情况,并从对准精度和对准时间上证明了算法的有效性。
(References):
[1] Hong Woonseon, Han Kyungjun, Lee Chulsoo, Paik Boksu. Three stage in flight alignment with covariance shaping adaptive filter for the strapdown inertial navigation system(SDINS)[C]//AIAA Guidance, Navigation and Control Conference. Toronto, Ontario, Canada, 2010: 355-361.
[2] 肖烜, 王清哲, 付梦印, 等. 里程计辅助陆用惯导行进间对准方法[J]. 中国惯性技术学报, 2012, 20(2): 140-145. Xiao Xuan, Wang Qing-zhe, Fu Meng-ying, et al. INS in-motion alignment for land-vehicle aided by odometer [J]. Journal of Chinese Inertial Technology, 2012, 20(2): 140-145.
[3] Guo Z, Miao L J, Zhao H S, et al. An improved strong tracking UKF algorithm and its application in SINS initial alignment under large azimuth misalignment angles [J]. Acta Aeronautica Sinica, 2014, 35(1): 203-214.
[4] Gao Wei-xi, Miao Ling-juan, Ni Mao-lin, et al. Multiple fading factors Kalman filter for SINS static alignment application[J]. Chinese Journal of Aeronautics, 2011, 24(4): 476-483.
[5] 钱华明, 葛磊, 彭宇, 等. 多渐消因子卡尔曼滤波及其在SINS初始对准中的应用[J]. 中国惯性技术学报, 2012, 20(3): 287-291. Qian Hua-ming, Ge lei, Peng Yu, et al. Multiple fading Kalman filter and its application in SINS initial alignment[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 287-291.
[6] 秦永元, 朱新颖, 赵长山, 等. 舰载机捷联惯导自对准方案设计与仿真[J].中国惯性技术学报, 2008, 16(1): 28-33. Qin Yong-yuan, Zhu Xin-ying, Zhao Chang-shan, et al. Design and simulation on SINS self-alignment for carrier born aircraft[J]. Journal of Chinese Inertial Technology, 2008, 16(1): 28-33.
[7] Georgy J, Noureldin A, Korenberg M, et al. Low-cost three-dimensional navigation solution for PISS/GPS integration using mixture particle filter[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 599-615.
In-motion alignment based on strong tracking filter
ZHAO Xiao-ming1, ZHAO Shuai1, WANG Xiao-liang1, ZHOU Ling-feng2, WANG Qiang3
(1. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China; 2. Automation College, Harbin Engineering University, Harbin 150001, China; 3. Beijing Military Representative Assembly of Beijing Military Representative Office in Tianjin Area, Tianjin 300131, China)
A new odometer-aided in-motion alignment algorithm based on strong tracking filter (STF) is proposed for vehicles driving in complicated environment. The STF with multiple fading factors is used in the fine alignment stage based on the property that the sequences of residuals are mutually uncorrelated when Kalman filter gain is optimal. The algorithm can adjust multiple fading factors adaptively, so it is robust to unknown external disturbances. The state equations and observation equations of in-motion alignment algorithm is established, and eight groups of ground-based navigation experiments are carried out in three different road conditions. The results show that this method is effective in complicated environment, and the estimated accuracy of heading error angle is less than 3.6′ (1σ), which satisfy the requirements of the in-motion alignment.
strapdown inertial navigation system; in-motion alignment; Kalman filter; multiple fading factor strong tracking filter
U666.1
A
1005-6734(2015)02-0141-04
10.13695/j.cnki.12-1222/o3.2015.02.001
2011-11-14;
2012-01-20
国防重点预研项目(51309010303)
赵小明(1961—),男,研究员,博士生导师,从事组合惯性导航系统技术研究。E-mail:zhaoshuai06074@163.com
