等效源方法的适用性判定及源的优化布置

魏应三，王永生，沈 阳，靳栓宝，蒋国健

（1.海军工程大学动力工程学院，武汉 430033；2.海军工程大学舰船综合电子技术国防重点实验室，武汉 430033；3.中国科学院声学所北海站，山东青岛 266023）

等效源方法的适用性判定及源的优化布置

魏应三1，2，王永生1，沈 阳2，靳栓宝2，蒋国健3

（1.海军工程大学动力工程学院，武汉 430033；2.海军工程大学舰船综合电子技术国防重点实验室，武汉 430033；3.中国科学院声学所北海站，山东青岛 266023）

采用等效源方法建立了辐射体表面法向振速到场点声压的传递函数，实现了声场的数值预报。以相对速度误差为评价指标，对等效源法的求解精度进行了先验判定，提出了以1／2速度误差限制线来确定等效源法适用的频率范围，进一步以声辐射效率为指标对声压计算结果的合理性进行后验判定。分别针对单个频率点、多个频率点对等效源的位置进行优化，结果表明存在最优等效声源位置以满足辐射体表面法向振速的最佳匹配。将等效源的优化方法应用于具有声反射面的脉动球源及锥－柱组合壳体的辐射声场预报，预报结果与解析解及边界元法计算结果吻合较好，说明等效源法在工程上应用是可行的。

等效源；优化；声辐射

边界元法（BEM）是继有限元法（FEM）之后发展起来的一种数值方法，可实现物理问题有效降维，但是相对于传统的域方法如FEM、有限差分法，常规BEM求解方程的系数矩阵为满阵，导致解题规模受到了很大限制［1］。等效源方法（ESM）的提出则促进了BEM在工程上的应用。Chen等［2］提出通过在辐射体表面布置等效源，并通过匹配辐射体边界速度势法向导数来预报声场，但由于Chen将等效源布置在辐射体表面，存在积分奇异。Koopmann等［3－4］提出将等效源布置在辐射体内部可有效克服积分奇异。于飞等［5－6］对ESM作了深入的研究，并成功应用于声场的全息重建。吴绍维等［7］采用无单元ESM研究了自辐射近似解析解问题，并提出等效源必须位于实际辐射体内的一定范围内才能用于声场计算。另外，ESM的求解精度与等效源数量、位置及分析频率范围也密切相关［8］。研究这些因素对ESM计算结果的影响的文献较多，但绝大多数数值计算结果均采用相互检验，较少有文献对数值计算本身的可信性进行判定，导致计算结果本身的可靠性又没有判据校核。朱之墀等［9］在对管道声场的数值预报中采用声能守恒判据、动量守恒判据和质量守恒判据对计算结果进行判定，这些判据对于指导数值计算具有一定借鉴作用，尤其在没有解析解或实验值对比的情况下显得更为重要。本文借鉴文献［9］的思想，提出了“速度误差小于1／2”的先验判据和“声辐射效率小于1”的后验判据对ESM的数值计算结果的合理性进行了判定。

1 等效源原理

等效源的主要思想是：任何辐射体的声场可以由置于该辐射体内若干个不同声源强度的简单源产生的声场叠加［8］，这些源强可通过匹配辐射体表面的法向振速得到。当等效源强确定后，空间声场任一点r的声压可由如下积分方程得到：

则当辐射体表面的法向速度已知时，声源强度表示为a＝H+Vns，此处H+为H的广义逆。为保证声源强度解的唯一性，须保证M≤N。由于等效源方法避免了声源点与场点重合的现象，因此积分不会出现奇异。当辐射体内部的声源分布确定后，根据式（1）可确定辐射体表面∂D及外声场空间D+任意一点rfj的声压，即：

对于半无限域声辐射问题，将无限域中的格林函数G修正为半无限域中的格林函数即可。

2 等效源方法的适用性判定

2.1 先验判据

于飞等［8］提出了通过计算辐射体表面上的振速均方根误差来评估求解精度，为保证ESM的求解精度提供了先验判据，但该方法无法确定ESM的适用频段的截止频率。本文在文献［8］的基础上，提出了一种相对振速误差Verror来评估ESM求解精度，并确定ESM适用频段的截止频率，

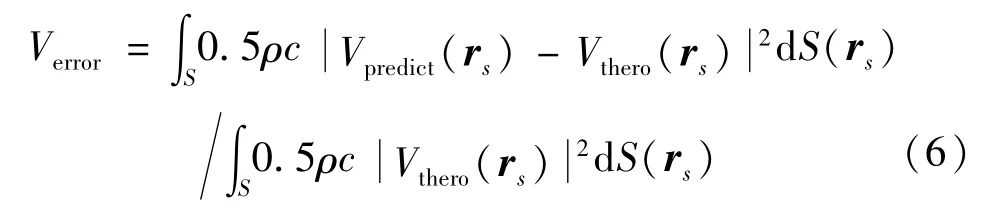
式中，Vthero为给定的辐射体表面法向振速，Vpredict为根据等效声源强度预报的辐射体表面法向振速。上式分母表示辐射体表面的等效辐射声功率，分子表示“绝对误差波”［8］所辐射的功率。通过求解不同频率的振速误差可得到误差曲线随频率的变化，该曲线与“1／2误差限制线”的交点所对应的频率即为截止频率。本文通过对脉动球源、一阶球源、活塞球源声辐射计算，结果表明当Verror小于1／2时，数值解与理论解吻合较好。

球源基本参数为：球源半径rs＝1 m，声速1 500 m／s，密度1 000 kg／m3。等效源所在球面半径为r0，且与脉动球源同心，距离d＝rs－r0。分析脉动球源时，球源以0.001 m／s的速度脉动；分析一阶球源时，球源沿x方向以0.001 m／s的速度振动。在此算例中，球源内部的简单等效源的数量等于辐射体表面的节点数量。图1（a）、（b）分别为脉动球源、一阶球源的速度误差曲线，图1（c）、（d）则为相应的声功率对比结果。以1／2速度误差限制线来确定截止频率，如图1（a）、（b）所示。当分析频率远低于该截止频率时，基于ESM计算的声功率与理论值吻合较好，而当分析频率接近截止频率时，受质点速度与声压预报精度的双重影响，辐射声功率的预报值会出现3～6 dB的误差，如图1（c）中d＝0.92以及图1（d）中d＝0.98的情况，说明采用ESM进行声场预报时，分析频率上限不能太接近截止频率。当分析频率超过截止频率时，声功率误差显著增加。

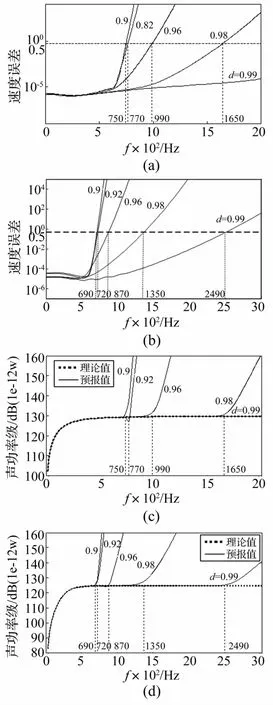
图1 球源的速度误差及辐射声功率.（a）、（b）依次为脉动球源、一阶球源在等效源不同布置位置时的速度误差；（c）、（d）为相应的球源辐射的声功率Fig.1 Velocity error（a），（b）and sound power（c），（d）of the pulsating sphere，first order sphere

Verror小于1／2的物理意义在于：当ESM预报的振源表面等效辐射声功率误差小于3 dB的限制线时，认为ESM求得的源强的精度能满足下一步求解声压的要求，至于ESM求得的声压是否合理，则需根据后验判据来判定。

2.2 后验判据

对于规则辐射体声辐射问题，其数值计算的准确性可用解析解检验。对于复杂结构的声辐射问题，在无解析解时除了用先验判据来判定EMS外，还需声场的后验判据来检验。本文提出的先验判据实际上是用均方振速来刻化，而当声压与质点速度都已知时则可用声功率与等效辐射声功率的比值，即辐射效率来表征。根据声能守恒原则，辐射效率须小于1，故可用辐射效率作为后验判据。

以更复杂的活塞球源为例，球源基本参数同上，在球坐标系（r，θ，φ）下，球源表面只有在张角φ≤60°范围内法向振速为0.001 m／s，其它范围内振速为0。图2（a）所示为r0＝0.25时球源的速度误差曲线，图2（b）为活塞球源等效辐射声功率、辐射声功率理论值及预报值的对比结果。分析知，当无量纲频率k rs＞3.15时，ESM不满足先验判据，如图2（a），与此同时辐射声功率预报值超过了等效辐射声功率的理论值（123.7 dB），后验判据也不满足，如图2（b）；而当k rs＜3.15时，ESM同时满足先验判据和后验判据，预报值与理论值吻合较好。

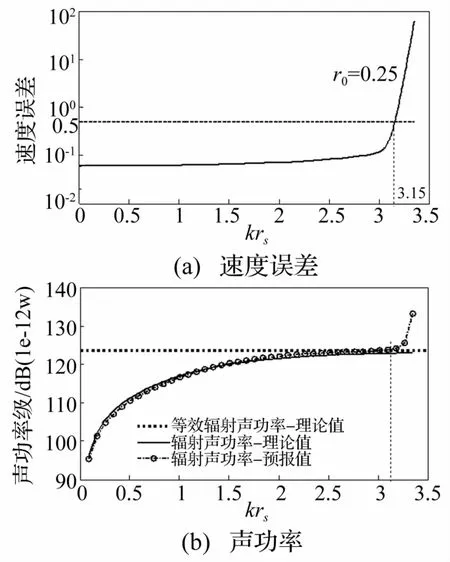
图2 活塞球源的速度误差及辐射声功率Fig.2 Velocity error（a）and sound power （b）of the piston source of the sphere

3 等效源的优化布置

3.1 单目标优化

等效源的位置对ESM的计算结果有较大影响，不同等效源位置所对应的截止频率也不同。因此在工程应用中就存在等效源位置的优化，以使截止频率尽可能的高。下面仍然以活塞球源为例，对给定某一频率下的等效声源位置进行寻优。假设简单等效源所在球面与活塞球源同心，优化变量为等效源所在的球面半径r0，其半径改变时，等效源的空间坐标等比例地改变，其中等效源的数量保持不变。为避免等效声源靠近辐射体边界而出现奇异积分，此处令0＜r0／rs＜0.9。

考虑优化问题：

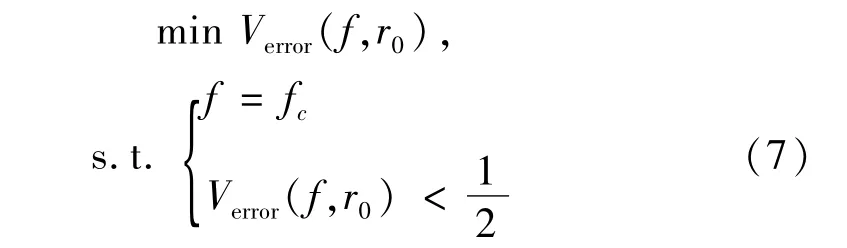
令fc＝800 Hz，对应无量纲频率krs＝3.35，通过变r0，得到不同r0对应的速度误差如图3所示。结果表明，当0.33＜r0／rs＜0.77时速度误差皆在1／2误差限制线以内，说明等效声源布置在此范围内时截止频率皆不低于3.35；当r0／rs＝0.75时，速度误差存在最小值，说明当等效声源布置在0.75rs的球面上时可实现振速的最佳匹配，经计算此时的无量纲截止频率为3.5，说明分析频率上限在截止频率之前，满足先验判据。为验证上述结论，分别取r0／rs为0.2、0.35、0.75、0.8，对活塞球源的辐射声功率进行预报如图4所示。当r0／rs取0.35（对应的无量纲截止频率为3.38）、0.75时，在分析频率0＜krs＜3.35范围内预报值与理论值皆吻合较好，其中r0／rs取0.75时预报精度最高；当r0／rs取0.2、0.8时，由于这两个位置对应的速度误差皆大于1／2，相应的无量纲截止频率分别为3.02、2.94，达不到3.35，因此预报值在频率范围3.1＜krs＜3.35内皆出现较大误差。

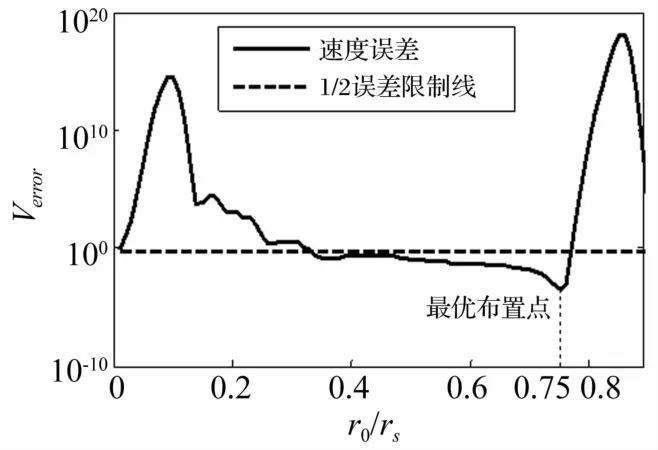
图3 krs＝3.35时单频优化结果Fig.3 Optimized result for single frequency krs＝3.35

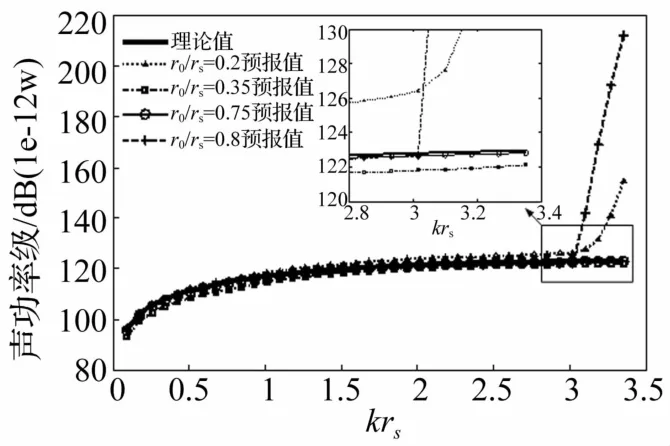
图4 不同等效源位置时的辐射声功率Fig.4 Sound power for various locations of the source

3.2 多目标优化

仍然以3.1节问题为例，考虑如下优化问题：

将该优化问题转化为单目标优化问题：

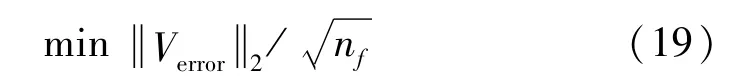
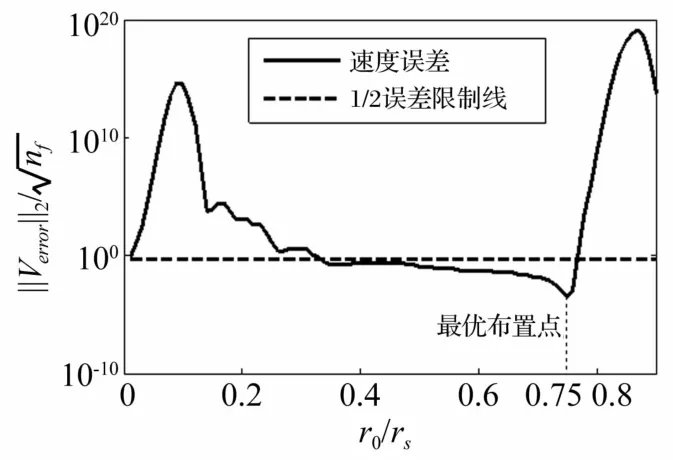
图5 多个频率点优化结果Fig.5 Optimized result formulti frequencies

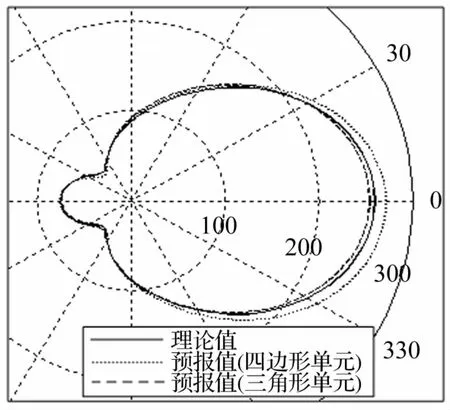
图6 krf＝8.38时的声指向性图Fig.6 Sound directivity at krf＝8.38

4 应用案例

4.1 具有声反射面的脉动球源的声辐射

脉动球源参数同2.1节中的脉动球源，分析频带0～800 Hz，反射面距离球心5 m，声反射系数为1，等效源位于与脉动球源同心、半径为0.01 m的球面上，辐射体采用三角形单元离散。经计算在分析频段内速度误差皆小于1／2，同时声辐射效率小于1，满足先验判据和后验判据。图7为空间场点P（5，0，5）处的声压预报值与理论值，吻合较好；图8为反射面在krs＝0.8时的声压分布，预报值与理论值也吻合较好，验证了方法的可信性。

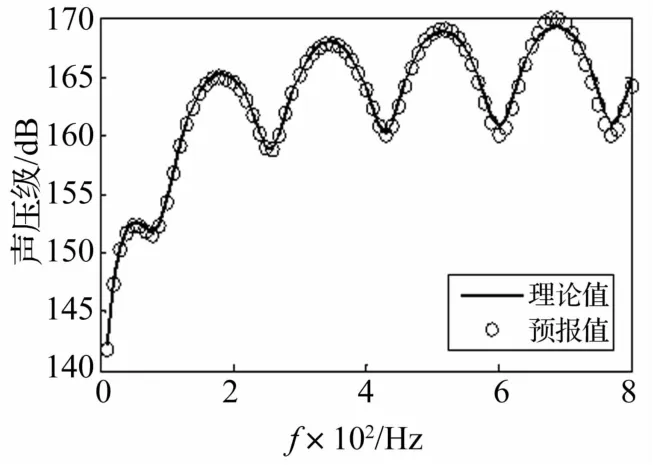
图7 P点处的声压曲线Fig.7 Sound pressure at point“P”

图8 krs＝0.8时声反射面上的声压分布Fig.8 Sound pressure at the reflecting plane at krs＝0.8

4.2 锥－柱组合结构的声辐射

图9所示结构由锥壳段与柱壳段组成，相关形状参数、材料参数及激励参数见文献［10］。此例中仍然将等效声源布置在球面上，其中球心限定在锥柱壳体的轴心线上，球面半径以使球面不超过组合壳体为限，优化变量为球面半径、球心位置。经计算，当等效源所在球面半径取0.15m，球心距离左端面0.3m时速度误差达到最小值，且同时满足先验判据和后验判据。分别采用ESM和BEM计算组合壳体的水下辐射声功率如图10所示，在整个分析频段范围内二者吻合较好，说明本文提出的等效源优化方法可用于水下辐射噪声的工程预报。

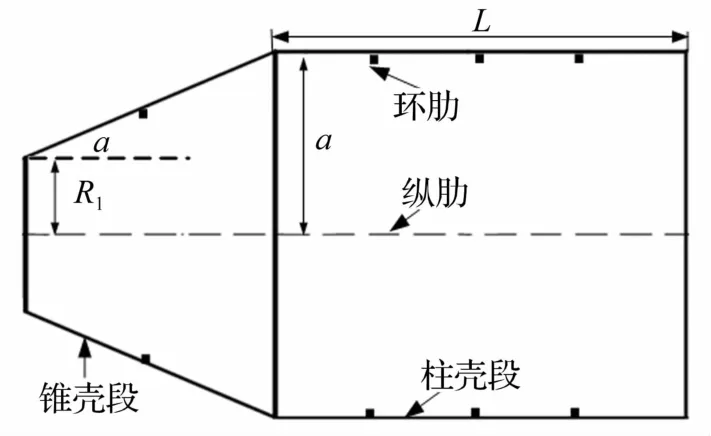
图9 组合结构示意图Fig.9 Scheme of the coupling structure

图10 水下辐射声功率Fig.10 Radiated underwater sound power

5 结 论

本文从基本的脉动球源、一阶球源、活塞球源声辐射问题中经验地提出了以1／2速度误差限制线作为ESM适用性的先验判据，以声辐射效率作为后验判据。最后通过两个案例对ESM的适用性进行了验证。得到如下结论：等效源位置对截止频率影响较大，对于某一频率（或频段）的声场计算，存在最优声源位置以满足辐射体表面法向振速的最佳匹配，此时ESM声场预报精度能够满足工程需要。

［1］Nishimura N.Fastmultipole accelerated boundary integral equationmethods［J］.Appl Mech Rev，2002，55（4）：299－324.

［2］Chen LH，Schweikert D G.Sound radiation from an arbitrary body［J］.The Journal of the Acoustical of Ameirca，1963，35（10）：1626－1632.

［3］Koopmann G H，Song L，Fahnline J.A Method for computing acoustic fields based on the principle of wave superposition［J］.The Journal of the Acoustical of Ameirca，1989，86 （5）：2433－2438.

［4］Song L，Koopmann G H，Fahnline J.Numerical errors associated with themethod of superposition for computing acoustic fields［J］.The Journal of the Acoustical of America，1991，89（6）：2625－2633.

［5］于飞，陈心昭，李卫兵.空间声场全息重建的波叠加方法研究［J］.物理学报，2004，53（8）：2607－2613.YU Fei，CHEN Xin-zhao，LIWei-bin.Investigatio on holographic reconstruction of sound field using wave superposition approach［J］.Acta Physica Sinica，2004，53（8）：2607－2613.

［6］李加庆，陈进，杨超.基于波束形成和波叠加法的复合声全息技术［J］.声学学报，2008，33（2）：152－158.

LI Jia-qing，CHEN Jin，YANG Chao.A hybrid acoustic holography technique based on beamforming and wave superposition algorithm［J］.Acta Acustica，2008，33（2）：152－158.

［7］吴绍维，向阳，夏雪宝.基于无单元声波叠加的自辐射近似解析表达研究［J］.振动与冲击，2014，33（7）：79－85.

WU Shao-wei，XIANG Yang，XIA Xue-bao.Approximate analytical expressions of self-radiation termsincluding acoustic pressure and velocity based on element free acoustic superposition［J］.Journal of Vibration and Shock，2014，33（7）：79－85.

［8］于飞.基于波叠加方法的声全息技术与声学灵敏度分析［D］.合肥：合肥工业大学，2005.

［9］朱之墀，李沛滋，王治国.管道声传播数值计算与实验结果比较［J］.声学学报，1988，13（1）：1－8.

ZHU Zhi-xi，LI Pei-zi，WANG Zhi-guo.Numerical solution compared with experimental result for sound propagation in ducts［J］.Acta Acustica，1988，13（1）：1－8.

［10］魏应三，王永生.锥－柱组合壳体声辐射影响因素研究［J］.振动与冲击.2012，31（22）：174－178.

WEIYing-san，WANG Yong-sheng.Study of the effect factors on acoustical characteristics of coupled cylindrical-conical shell［J］.Journal of Vibration and Shock，2012，31（22）：174－178.

Applicability criterion of equivalent sourcesmethod and locating optim ization of sources

WEIYing-san1，2，WANG Yong-sheng1，SHEN Yang2，JIN Shuan-bao2，JIANGGuo-jian3

（1.College of Marine Power，Naval University of Engineering，Wuhan 430033，China；2.National Key Laboratery of Science and Technology on Vessel Integrated Power System，Naval University of Engineering，Wuhan 430033，China；3.Institute of Acoustics，The Chinese Academy of Sciences，Qingdao 266023，China）

Based on the equivalent sourcemethod（ESM），the transfer function from the normal vibration velocity of a radiation body's surface to the sound pressure of a field point was built and the prediction of a sound field was realized.To evaluate the accuracy of ESM in prior，the relative velocity error indexwas used and a 1／2 restrict-line of the velocity error was given to determine the frequency range for which ESM is applicable.The rationality of the sound pressure calculation results were evaluated via the sound radiation efficiency index afterward.Then the locations of the equivalent sourceswere optimized for single frequency points andmulti-frequency points，respectively.The results showed that there is an optimal sound source location to satisfy the bestmatch of the normal vibration velocity of the radiation surface.Finally，the ESM optimization algorithm was applied to predict the radiation sound fields of a pulsating sphere with a sound reflection surface and a coupled conical-cylindrical shell，the prediction results agreed wellwith those of the analyticalmethod and BEM.The results indicated that the ESM is applicable for engineering problems.

equivalent source；optimization；sound radiation

TB553；U663

A

10.13465／j.cnki.jvs.2015.21.035

国家自然科学基金项目（51409256，51307177，51309229）；海军工程大学自然科学基金引导项目（HGDYDJJ13003）

2014－06－17 修改稿收到日期：2014－10－23

魏应三男，博士，讲师，1984年5月生

王永生男，博士，教授，1955年10月生邮箱：yongshengwang666＠126.com