复合材料层合板声功率及灵敏度研究

吴锦武，薛晓理，彭文辉

（南昌航空大学 飞行器工程学院，南昌 330063）

复合材料层合板声功率及灵敏度研究

吴锦武，薛晓理，彭文辉

（南昌航空大学 飞行器工程学院，南昌 330063）

采用分层理论结合有限元模型分析复合材料层合板结构的振动特性，并用声辐射模态理论进行结构声辐射分析。在此基础上，分析声功率关于设计参数的灵敏度，推导声功率灵敏度的表达公式。以四层复合材料层合板为例，着重对声功率关于层合板结构铺层角度和铺层厚度的灵敏度进行了分析研究。数值计算结果显示在层合板基频处，辐射声功率达到最大值，同时在该处灵敏度有明显的升降过程。另外，对于低噪声层合板应以±45°对称的铺设将是最为恰当的设计方案。

声学；声辐射；声功率灵敏度；层合板

研究结构声功率及其灵敏度，是结构低噪声设计重要内容之一。声功率灵敏度是指声功率关于设计参数的变化率，能够量化各设计参数对声功率的影响程度，以声功率灵敏度为指标，可通过定量修改设计参数，降低结构辐射噪声，是结构优化设计的重振动与声优化设计而言，如基于经典层合板理论，结要途径[1]。

近年来,对于一般振动板结构声功率灵敏度的研究越来越多。例如姜哲等[1，2]对薄板结构和阻尼板结构的声功率灵敏度进行了研究，杜向华等[3]分析了三类设计变量的声功率灵敏度，对于层合板结构有限元方法研究层合板振动特征值对铺设角度的灵敏度[4]以及层合板辐射声功率优化设计[5，6]。由于层合板结构参数众多，其对声功率的贡献不尽相同，即存在不同的声功率灵敏度。因此，有必要对复合材料层合板结构的声功率灵敏度进行分析。

本文主要基于分层理论结合有限元模型分析振动特性，通过声辐射模态计算结构声功率。着重就复合材料层合板的声功率及其关于铺设角度和铺层厚度的灵敏度展开分析研究。

1 声辐射模态模型

任意形状的振动结构表面S以圆频率ω振动，向无界空间V辐射声。在空间V中充满均匀介质，介质的密度为ρ，声速为c。设振动表面S上的法向振速为U，辐射声压为P。对于单频振动，结构的辐射声功率可表示为[2,7]

2 层合板动力学方程

通过分层理论，对每一层板在板厚方向采取二次插值，如图1所示。

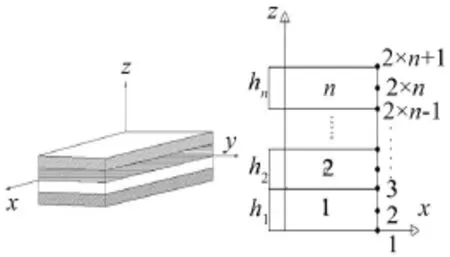
图1 层合板的物理模型和坐标关系

层合板位移场可表达为[7]

其中式（4）中U(x,y,z,t)，V(x,y,z,t)，W(x,y,z,t)分别为x,y,z方向位移，n为铺设层数，2n+1为插值面数，ui(x,y,t)，vi(x,y,t)，wi(x,y,t)为第i个插值平面内x,y,z方向位移，Ψi(z)为插值展开系数，其值见参考文献[7]。

根据有限元理论，式（6）中ui(x,y,t)，vi(x,y,t)，wi(x,y,t)表示为

式（5）中m为有限元单元节点数。Nk(x,y)为形函数表达式，uk,vk,wk为有限元节点k处的x,y,z坐标，T(t)为时间函数。根据有限元理论，本文采用四节点矩形单元，将式(5)和四节点形函数表达式代入式(4)，可得单元形函数矩阵N：

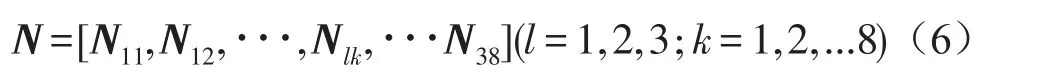
根据弹性力学位移－应变关系，可得到单元应变矩阵

其中元素Bij见参考文献[7]。

根据转轴公式，当M坐标系与材料正轴坐标存在偏轴角，即层合板存在铺设角度时，位移应变关系可表达为

其中式（8）中D为刚度矩阵，改变铺设角度，刚度矩阵会发生改变。得到矩阵B和D后，单元刚度矩阵K和单元质量矩阵M以及阻尼矩阵C可以表示为

其中α，β分别为质量和刚度的比例系数。此时结构总动力方程为

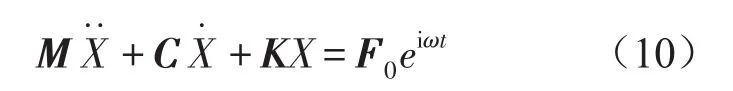
其中X为振动法向位移向量。F0为激励力幅值向量。层合板各阶固有频率可由行列式 |求得。

设在简谐力激励下结构法向位移响应形式为：X=X0eiωt，此时结构动力方程为

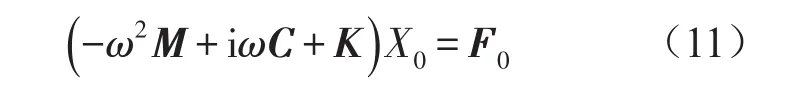
振动法向速度对设计参数h求偏导为

（11）两边对设计参数求偏导，结合式（12）可得

其中刚度矩阵K和质量矩阵M可直接对设计参数求偏导。已知振动速度对设计变量导数，可由式（2）得到声功率灵敏度。

由式（9）和（13）可知：改变层合板纤维铺设角度可改变层合板结构刚度；改变层合板结构厚度会影响结构质量。因此层合板结构纤维铺设角度和层合板厚度的改变会影响层合板结构的声功率。

3 算例及分析

3.1 不同铺设角度声功率及其灵敏度分析

四层四边固支复合材料层合板长、宽、厚度分别为a=0.3 m，b=0.3 m，t=0.002 m。弹性模量分别为E1=124 Gpa，E2=E3=10.3 Gpa；剪切模量为G12=G23=G31=7.17 Gpa；泊松比μ=0.28，层合板铺设角度取常见四种形式：[90°/0°]2，[±15°]2，[±30°]2，[±45°]2，在板中心施加单位激励力F0，最大激励频率为1 000 Hz。此时不同铺设角度下层合板结构固有频率如表1所示。

表1 不同铺设角度层合板前6阶固有频率

根据式（2）可得到不同铺设角度四层固支层合板声功率级与激励频率关系，所得结果如图2。

图2 不同铺设角度层合板辐射声功率级

由图2可知：在低频时，不同铺设角度时层合板结构声功率相差不大，而且在基频时声功率达到最大；在高频时，层合板以[±45°]2铺设时声功率较小，因此对于低噪声层合板结构设计应尽可能以[±45°]2铺设为佳。

从式(9)可知：改变铺层角度可改变单元刚度矩阵。因此，声功率关于铺层角度的灵敏度可转化成偏轴刚度矩阵对铺层角度求导问题。通过计算得到层合板声功率灵敏度与外激励频率的关系，所得结果如图3。

由图3可知：不同铺设角度时，层合板结构在基频处声功率灵敏度有明显的升降过程，因此在结构设计时应避免激励频率与基频接近。另外在低频时，[90°/0°]2铺设时层合板结构声功率灵敏度最大，在高频时，不同铺设角度下的声功率灵敏度随外界激励频率变化趋势基本保持一致。

图3 不同铺设角度层合板声功率灵敏度

3.2 不同铺层厚度声功率及其灵敏度分析

厚度影响层合板结构质量，从而影响层合板结构声功率。在相同铺设角度和层数的情况下，本文分两种情况来讨论结构声功率及其灵敏度：

1）总铺层厚度不同，每层皆为均匀分布；

2）总铺层厚度相同，但每层厚度不同。

当总铺层厚度不同，以四层厚度均匀分布的复合材料层合板为例，其材料性能参数同3.1所示，其中层合板铺设角度为[45°/-45°]2，总铺层厚度分别为h1=1.5 mm，h2=2 mm，h3=2.4 mm，h4=3 mm。计算四边固支边界条件下中点激励层合板辐射声功率及其灵敏度。

通过计算可得到总铺层厚度不同下层合板结构的前六阶固有频率，结果如表2所示。由表2可知：随着层合板结构厚度增加，对应的固有频率值增大。根据式（4）可得到不同总铺层厚度固支层合板声功率级与外激励频率的关系，所得结果如图4所示。

由图4可知：不同总铺层厚度的层合板都在基频时声功率达到最大，板厚为1.5 mm时声功率峰值最大，2.4 mm时峰值最小，即随着层合板结构厚度的增加，声功率的峰值逐渐减小。在高频时，不同总铺层厚度的层合板结构声功率变化不明显。

从单元刚度矩阵K表达式(9)可知：铺层厚度通过改变单元应变矩阵B来改变单元刚度矩阵。由参考文献8可知：插值函数的取值与铺层厚度直接相关。因此，声功率关于铺层厚度的灵敏度实际可以转化成插值函数取值对铺层厚度求导问题。通过计算得到不同总铺层厚度层合板声功率灵敏度与外激励频率的关系，所得结果如图5。

由图5可知：总铺层厚度不同时，层合板结构在基频处声功率灵敏度有明显的升降过程，因此在结构设计时应避免激励频率与基频接近。另外在低频时，铺层厚度为1.5 mm时层合板结构声功率灵敏度最大，2.4 mm时层合板结构声功率灵敏度最小，在高频时，不同总铺层厚度下的层合板声功率灵敏度随外界激励频率变化趋势基本保持一致。

表2 不同总铺层厚度层合板前六阶固有频率

图4 不同总铺层厚度层合板辐射声功率级

图5 不同总铺层厚度层合板声功率灵敏度

当层合板总铺层厚度相同，但每层厚度不同时，同样以四层复合材料层合板为例，其材料性能参数见3.1节所示，层合板铺设角度为[45°/-45°]2，板的总厚度都等于2 mm的情况下，各铺层厚度采用等厚度和不等厚度两种分布方式。等厚分布为[0.5/0.5/0.5/0.5]mm，不等厚分布取3种中心对称分布情况分别为：[0.2/0.8/0.8/0.2]mm、[0.4/0.6/0.6/0.4]mm和[0.8/0.2/0.2/0.8]mm。

通过计算可得到单层铺层厚度不同下层合板结构的前6阶固有频率，结果如表3所示。由表3可知：总厚度相同的情况下，不同单层铺层厚度对层合板结构基频影响不大。

表3 不同单层铺层厚度层合板前六阶固有频率

根据式（5）可得到不同单层铺层厚度固支层合板声功率级与外激励频率的关系，所得结果如图6所示。由图6可知：在低频时，不同单层铺层厚度时结构声功率相差不大，而且在基频时声功率达到最大；在中频时[0.8/0.2/0.2/0.8]mm铺层的层合板声功率最先出现衰减，[0.2/0.8/0.8/0.2]mm铺层的层合板声功率最后出现衰减，说明外面两层铺层厚度较大可以优先降低声功率；在高频时，不同单层铺层厚度的层合板结构声功率基本保持一致。

通过计算得到不同单层铺层厚度层合板声功率灵敏度与外激励频率的关系，所得结果如图7。

由图7可知：单层铺层厚度不同时，层合板结构在基频处声功率灵敏度有明显的升降过程，因此在结构设计时应避免激励频率与基频接近。在高频时，不同单层铺层厚度的层合板结构声功率灵敏度基本保持一致。

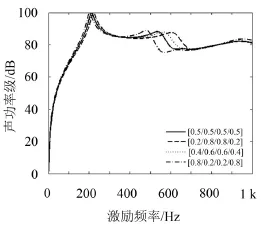
图6 不同单层铺层厚度层合板辐射声功率级

4 结语

本文利用有限元与声辐射模态对复合材料层合板结构的辐射声功率及其关于设计参数的灵敏度进行了研究，重点推导了辐射声功率对铺设角度和铺层厚度的灵敏度分析过程。以四边固支层合板为例，数值计算结果表明：1）对于低噪声层合板结构设计应尽可能以[45°/-45°]2铺设为佳；2）在层合板基频处，辐射声功率达到最大值，同时在该处灵敏度有明显的升降过程。即低噪声设计时，应尽可能避免接近基频附近。

Analysis of Sound Power and Sensitivity of Composite Laminate Plates

WU Jin-wu,XUE Xiao-li,PENG WEN-hui
(School ofAircraft Engineering,Nanchang HangKong University,Nanchang 330063,China)

The vibration characteristic of a composite laminate plate was studied by using FEM and laminate plate theory,and the sound radiation mode method was used to analyze the structural sound radiation of the plate.Then,the sound radiation sensitivity to design parameters was analyzed by using the sound radiation power and its expression was formulated.A four-layer composite plate was used as an example,and the sound power sensitivities to the ply angles and thickness of the plate were investigated.The numerical simulations show that the 45°symmetric ply angle is the best for the laminate plate, and the noise of the plate can be reduced significantly.In addition,the acoustic power reaches the maximum at the fundamental frequency of the laminate plate.Meanwhile,the acoustic power sensitivity has a peak value also at this frequency.

acoustic;sound radiation;sound power sensitivity;laminate plate

TB132

：A

10.3969/j.issn.1006-1335.2015.01.024

1006-1355(2015)01-0119-04+126

2014－06－25

国家自然科学基金项目(51265038)

吴锦武(1976－)，男，博士，硕士生导师，主要研究方向：振动与声研究。E-mail:jinwu.w@hotmail.com