压电晶体在纵波声场中三维模型的建立与研究

薛婷婷

（ 辽宁何氏医学院，辽宁 沈阳110163）

1 超声探头发射声场的研究

1.1 波源轴线上的声压分布

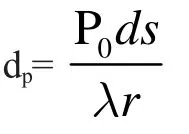
根据波源叠加原理， 将圆盘形活塞换能器上每一个点波源在轴线上P 点引起的声压进行线性叠加， 便可得到P 点的声压。故将整个波源面积积分便可得到波源轴线上任意一点声压，其表达式为：

当x≥2Rs时，

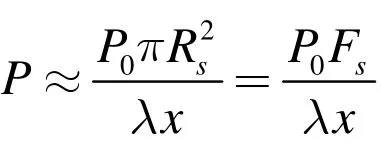
由该式可以看出，当x≥3Rs/λ（ πRs2/2λx≤π/6）时，圆形压电晶片的声压分布与波源面积成正比，与距离成反比。

1.2 声轴横截面上声场的声压分布

点波源ds 在距波源充分远处任意一点P（ r，θ） 处的声压为：

整个圆形活塞换能器在点P（ r，θ）处辐射的总声压为：

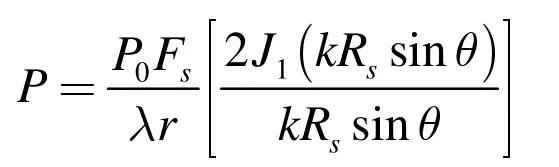
可将球面坐标表达式转化为笛卡尔坐标系下的函数表达式：

2 声场的模拟及可视化

2.1 应用平台Matlab

通过编写Matlab M 语言，用形象、具体的图形来显示出抽象的超声波声场的分布情况，从而更准确地分析其特征。

2.2 三维声场的声压分布

图1 和图2 为对于半径R 为12 毫米，波长λ 为1.5 毫米的圆形晶片，波源起始声压P0为常数，介质为液体时，整个空间的声压分布。

如图1 所示，在XOY、YOZ 以及XOZ 平面内做切片，得到声场声压分布情况。 由于各切片之间会出现相互遮挡的情况，这里采取透明处理方法解决。 但是由于切片过多， 透明处理后会使图像虚化，因此采用等值面抽取技术，抽取声压幅值分别为两个、三个和四个大气压的情况，并进行透明处理，得到图2。

图1 圆形声源整个声场声压分布

图2 圆形声源声场声压等值面分布

3 结果讨论

3.1 半径大小对声压分布的影响

以液体为超声波的传播介质，在波源的起始声压P0为常数、发射频率为定值的情况下，对不同半径大小的圆形压电晶片进行模拟。

图3 圆形晶片不同半径大小的声压分布

从图中可以看出，在波长为定值时，随着圆盘形压电晶片的半径增大：a.半扩散角减小、近场区长度增加；其主瓣越来越窄，能量更集中，但同时旁瓣的数量也增多。 b.波源轴线上声压值越来越高，声场范围越来越集中。 由于波长是固定的，所以超声波的穿透距离是一定的，这样近场区的长度将决定实际的检测距离。 近场区长度越小，实际的有效检测距离也就越大，这时所需要的探头半径就比较小。 然而较小的探头半径将导致超声场的声束主瓣不集中， 造成仪器的检测精度下降，对医用诊断与治疗很不利。 因此，在针对不同要求的检测或诊断时，应该合理选择换能器的半径大小。

3.2 波长大小对声压分布的影响

同样以液体为超声波的传播介质，在波源的起始声压P0为常数的情况下， 对不同波长大小的圆盘形活塞换能器进行模拟。

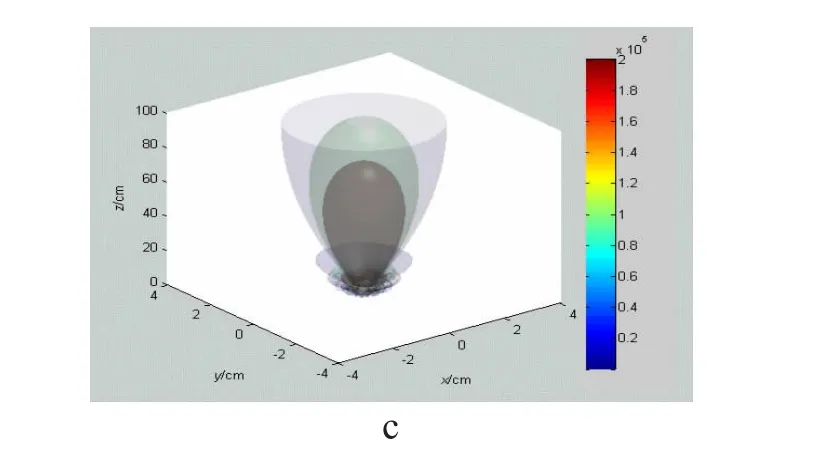
图4 圆形活塞换能器不同波长大小的声压分布

由图可以看出， 在圆盘换能器半径为定值时， 随着波长增大：a.半扩散角增大、近场区长度减小；其声束主瓣越来越宽，超声波能量变得扩散，但同时旁瓣的数量减少。b.轴线上的声压幅值越来越低，声场范围越来越扩散。 由于半径大小是固定的，所以超声波的穿透距离随着波长的增加而增加， 即检测深度增加。 近场区长度随着波长的增加而减少，所以有效的检测距离会增加。 但随着波长的增加，声束主瓣的聚集程度下降，导致检测的精度下降。 例如检测距离较深的诊断，如腹腔诊断等，就需要牺牲一部分精确度，选用波长相对较长的探头。

4 结论

应用超声波基本理论，在大量数学定律的支持下，对超声声压的分布表达式进行推导，应用Matlab 仿真软件对圆形压电晶体进行三维模型的建立。 从多个角度、 多个方面讨论分析圆形压电晶片所发射的声场，了解其分布特征。 并讨论不同参数的变化对声场分布情况的影响，可为不同环境下超声探头的选用作为参考依据。