基于多重分形理论与神经网络的齿轮故障诊断

褚青青，肖 涵，吕 勇，杨志武

（武汉科技大学机械自动化学院冶金装备及其控制教育部重点实验室，武汉 430081）

基于多重分形理论与神经网络的齿轮故障诊断

褚青青，肖 涵，吕 勇，杨志武

（武汉科技大学机械自动化学院冶金装备及其控制教育部重点实验室，武汉 430081）

针对齿轮故障振动信号具有多重分形特征，提出多重分形与神经网络相结合的机械故障诊断方法。采用多重分形理论计算出振动时间序列的多分形谱f（α）和广义分形维数D（q），并将多分形谱能和广义分形维数谱能作为特征量，构成二维特征向量。将该特征向量作为概率神经网络的输入参量，对采自齿轮故障台的振动信号进行故障分类。作为对比，将关联维数作为特征量输入同样参数的概率神经网络并进行故障识别，结果表明，所提出的方法具有更高的识别率。

多重分形理论；神经网络；多分形谱；广义分形维数

广泛应用于各种机械设备中的齿轮一旦出现故障，会引起机械设备无法正常工作，造成严重的经济损失甚至威胁到人的生命安全。齿轮振动信号的故障诊断方法已经有很多［1－2］，如常见的时频域分析，谱分析，傅里叶变换等。但齿轮振动信号所具有的非平稳、非线性特征往往导致在提取其频谱中的特征频率时出现困难［3］，无法准确反映信号的非线性特征。分形理论被证明是刻画非平稳时间序列的长程相关性的可靠方法之一［4］，研究表明，齿轮振动信号具有分形特性，这种分形特征为齿轮的故障诊断提供了一种有效的特征描述方法，利用分形方法可以较准确地提取非线性振动信号的特征。很多学者应用单分形理论提取振动信号特征并用于故障诊断，但单分形分析只能反映振动时间序列的整体信息，对信号的局部特征刻画不足。多分形不仅反映序列的整体信息，而且能够清楚地展示出其局部信息，进而对复杂的振动信号进行准确描述［5－6］。

对于大多数客观存在的分形物体而言，仅用一个分形维数并不能完全刻画其结构。Grassberger系统提出多重分形理论，用广义分形维数和多重分形谱来描述分形客体，考虑了分形客体在分形支集的空间奇异性分布，因而在湍流、地震、图像处理等几乎所有涉及分形的领域迅速发展，并得到广泛应用［4－5，7］。多重分形谱能够反映整个分形结构上概率测度分布的比例、不均匀程度，能够全面描述振动信号的波动程度以及振动剧烈程度［8］。

多分形谱参数［5，9］，形态学分形维［10］，广义分形维数［11－13］等可以清晰地反映出振动信号的故障特征，洪时中等［7－8］指出多重分形谱参数和广义分形维数可以表征故障特征，但这些研究仅指出齿轮振动信号具有多分形特征，并未针对这一特征提出对应的诊断方法。由于实测信号中的噪声对分形维数的影响较大，为得到精确可靠的分形维数，必须先对实测的齿轮振动信号进行降噪处理［3，10］。首先将信号进行EMD降噪处理，然后采用多分形理论与神经网络相结合的方法对齿轮故障状态进行分类，并用实验来证实提出方法的可行性和有效性。

1 多重分形谱算法

多重分形奇异谱最先由Halsey等［4］给出，经过刻画定义于分形集上的归一化测度的奇异特性来研究其标度性。分布的奇异性由两个指数来刻画：奇异性强度α及对应的分布密度f（α）。分形奇异谱则是由α值的取值范围和函数f（α）确定。计算步骤如下：

（1）将时间序列｛xi｝，（i＝1，2，3，…，N）依次划分成尺度为λ（λ＜1）的一维小盒子，令ai（λ）为盒子尺度为λ的第i个小盒子内振动信号的所有幅值之和，振动信号的所有幅值之和为∑ai（λ），则定义概率测度为：

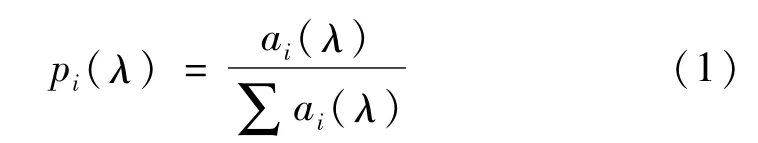
（2）由概率测度pi（λ）定义配分函数χq（λ），

其中，q为一个实参数，q的值可以取（－∞，+∞）之间的值，式（2）中pi（λ）＝0的情况除外，为避免pi（λ）＝0的情况，在计算之前先对序列进行归一化处理。当q达到一定值，q对多重分形谱已没有影响，q取值范围选取的标准为：当q改变1时，奇异指数的改变率Δα（q）＜0.2%［9，12］。

（3）配分函数χq（λ）与尺度λ之间存在幂指数关系：

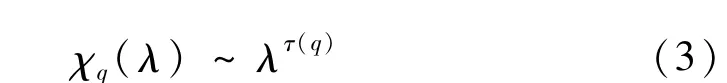
幂指数称为质量指数。对式（3）两边取对数得：

式中质量指数τ（q）即为配分函数与尺度的双对数曲线的斜率。

（4）由勒让德变换求得奇异指数α（q），计算公式为：

进而求得多分形谱f（α），其计算公式为：

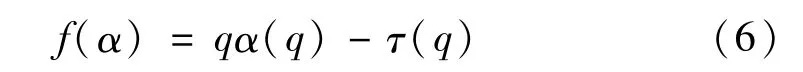
由质量指数τ（q）计算广义分形维数D（q），公式为：

当q＝2时，得到关联维数［13］D（2）。

2 齿轮振动信号的多重分形性与特征提取

2.1 齿轮振动信号采集

实验信号采自齿轮故障实验装置，齿轮传动实验台传动简图及实验装置的结构与测点示意图如图1所示。实验装置为单级齿轮传动，小齿轮安装在输入轴上，其齿数Z1＝20，大齿轮齿数Z2＝37，齿轮模数为3。负载由磁粉加载器产生。振动加速度传感器安装在输入端轴承座的垂直方向。点击转速为285 r／min，负载为0 N·m～20 N·m之间的随机状态。分别采集齿轮状态为正常、断齿、磨损和周节误差四种故障的振动信号。采样时间为2 s，采样频率2 048 Hz。

图1 齿轮传动实验台传动简图Fig.1 Transmission diagram of the gear transmission test bench

2.2 齿轮振动信号的多重分形特性

共采集齿轮四种故障状态（正常、磨损、断齿、周节误差）振动信号，每种状态采集20组数据。

为了提高结果的准确性和计算的高效性，首先用EMD方法对原始数据进行分解，将原始信号分为10层［10，14］，对齿轮正常和磨损状态信号取前两层，断齿状态信号取前三层，周节误差状态信号取前四层。然后对分解后的信号按式（8）进行归一化处理［15］。

式中xi为时间序列｛xi｝（i＝1，2，3，…，N）中的元素，xmin为时间序列元素中的最小值，xmax为时间序列元素中的最大值。根据前文q值范围选取标准，q的取值范围［－60，60］，取值间隔为3。通过式（1）和（2）计算得到齿轮振动信号的配分函数χq（λ）。以正常齿轮振动信号为例，其配分函数与尺度λ的双对数图如图2所示。

由图2看出配分函数χq（λ）与尺度λ的双对数曲线呈现很好的线性关系，表现出标度不变性［9］，表明齿轮振动信号具有多重分形性。

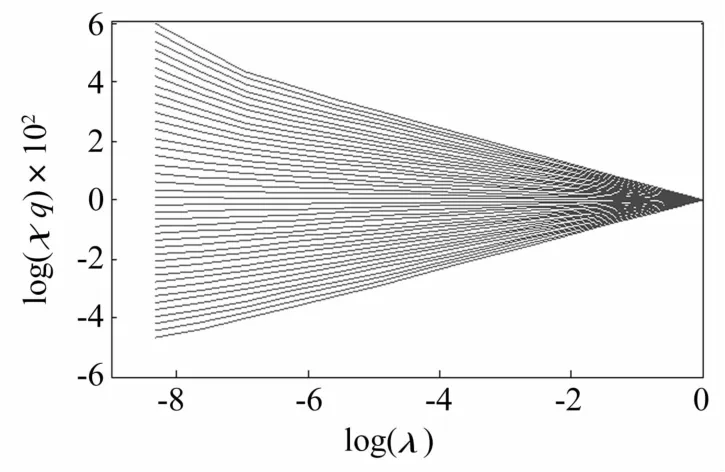
图2 正常齿轮振动信号对应的配分函数与尺度的双对数图Fig.2 The log-log graphs of the corresponding partition function and the size of normal gear state

由式（3）和式（4）计算得到质量指数τ（q），以正常齿轮振动信号为例，其质量指数与实参数q的关系曲线如图3所示。图中实线为过两个端点的直线，由图3看出τ（q）与q之间呈现非线性关系，也表明齿轮振动信号具有多重分形特征［4］。

图3 正常齿轮振动信号的质量指数与q的关系曲线Fig.3 The curves of the quality index and q of normal gear state

由式（5）、（6）计算得到多分形谱f（α）和奇异指数α，图4为多分形谱与奇异指数的关系曲线图。

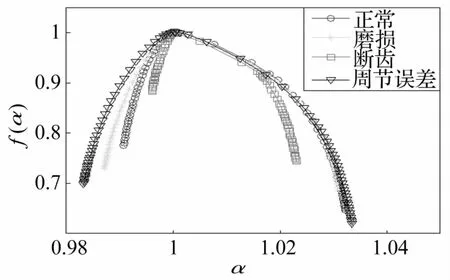
图4 齿轮的四种故障状态的多分形谱图Fig.4 Multifractal spectras of four types of gear fault states

由图4看出齿轮振动信号的多分形谱f（α）均为单峰函数，再次说明齿轮四种振动信号的多重分形性，但四种故障状态的奇异性又有不同。多分形谱f（α）是对分形结构上的复杂程度、不规则程度以及不均匀程度的一种度量。

由式（7）计算得到广义分形维数D（q），以正常齿轮为例，其广义分形维数与实参数q的关系曲线如图5所示。

由图5看出广义分形维数D（q）与q之间的关系，广义分形维数是随q增大而单调递减的函数，进一步表明齿轮振动信号的多重分形性。

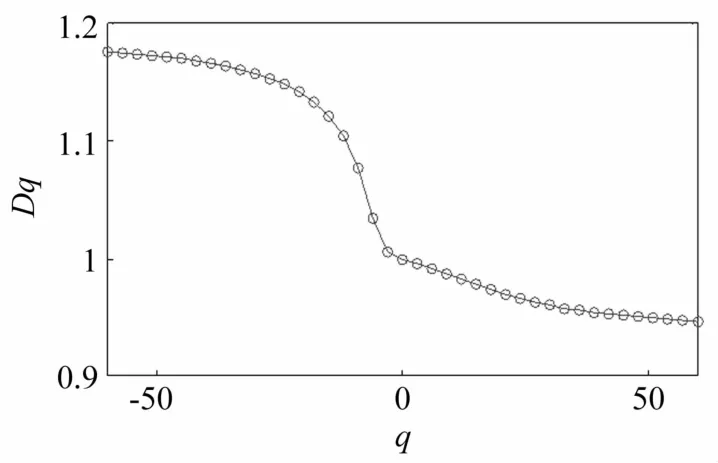
图5 正常齿轮振动信号的广义分形维数与实参数q的关系曲线Fig.5 The curves of the generalized fractal dimensions and q of normal gear state

2.3 齿轮振动信号的特征参数提取

从能量理论的角度出发，系统发生故障时故障状态的能量大小和空间分布也会发生变化，且各个故障状态的能量大小是不同的。因此，本论文采用多分形谱f（α）的二阶矩和广义分形维数D（q）谱的二阶矩作为特征量，构成二维特征向量。由式（7）计算得到广义分形维数D（q）的值。两个特征量的计算公式如下：

朱云博等［16］以多个多重分形谱参数及广义分形维数作为特征量，计算量大，本论文中利用多重分形谱和广义分形维数的二阶矩作为特征量，能有效提高计算速度。

3 PNN神经网络分析方法进行分类及结果分析

概率神经网络具有较强的对非线性问题处理和分类能力。其实质是基于贝叶斯最小风险准则发展而来的，PNN训练时间短，且分类正确率较高［17］。

通过研究分析多重分形谱能和广义维数谱能具有明确的物理意义，表达了时间序列内部的动力学机制，对机械系统状态的变化非常敏感，因此，适合作为表征系统状态的特征量。本实验研究中，每种故障状态采集20组振动信号，每种故障状态振动信号中的10组作为训练数据，利用概率神经网络首先对提取的训练样本进行学习训练，另外10组用作检验数据。所得结果见表1与表2。

表1 多分形与神经网络结合的机械故障诊断识别率Tab.1 Recognition rates ofm achinery fault diagnosis ofmultifractal com bined w ith neural network

表2 基于关联维数与神经网络的机械故障诊断结果Tab.2 M echanical fault diagnosis result based on the correlation dim ension and neural network

由表1、表2分类结果可以看出，运用多分形与神经网络结合的机械故障诊断方法对实验台的故障数据进行分类，其识别率更高。

4 结 论

本文提出将多分形理论与神经网络相结合的方法，然后应用于齿轮故障诊断，并用实验证实提出方法的可行性和有效性。不足之处是选择某一个无标度区计算，可能丢失一些振动信号信息，可以考虑基于多个无标度区间的多分形分析方法，以期得到振动信号的全部信息。

［1］林近山，陈前.基于多重分形去趋势波动分析的齿轮箱故障特征提取方法［J］.振动与冲击，2013，32（2）：97－101.

LIN Jin-shan，CHEN Qian.Gear box fault feature extraction methods based on multifractal detrended fluctuation analysis ［J］.Journal of Vibration and Shock，2013，32（2）：97－101.

［2］于功志，关德林，段树林，等.基于多重分形的齿轮故障特征提取方法［J］.大连海事大学学报，2009，35（1）：111－114.

YU Gong-zhi，GUAN De-lin，DUAN Shu-lin，et al.Gear fault feature extraction method based on multifractal［J］.Journal of Dalian Maritime University，2009，35（1）：111－114.

［3］李琳，张永祥，明廷涛.EMD降噪的关联维数在齿轮故障诊断中的应用研究［J］.振动与冲击，2009，28（4）：145－148.

LI Lin，ZHANG Yong-xiang，MING Ting-tao.Gear fault diagnosis based on correlation dimension preprocessed with EMD［J］.Journal of Vibration and Shock，2009，28（4）：145－148.

［4］蒲小勤.基于多重分形的图像识别研究［D］.西安：西北大学，2009：1－57.

［5］钟明寿，龙源，谢全民，等.基于分形盒维数和多重分形的爆破地震波信号分析［J］.振动与冲击，2010，29（1）：7－11.

ZHONG Ming-shou，LONG Yuan，XIE Quan-Min，et al.Analysis of the blasting seismic wave signals based on the fractal box dimension and multifractal［J］.Vibration and Shock，2010，29（1）：7－11.

［6］李彤，商朋见.多重分形在掌纹识别中的研究［J］.物理学报，2007，56（8）：4393－4400.

LI Tong，SHANG Peng-jian.Multifractal research in palmprint recognition［J］.Journal of Physics，2007，56（8）：4393－4400.

［7］洪时中，黄登仕.多重分形与地震［J］.四川地震，1991，1（1）：8－18.

HONG Shi-zhong，HUANG Deng-shi.Multifractal and earthquake［J］.The Earthquake in Sichuan，1991，1（1）：8－18.

［8］李国宾，关德林.振动信号多重分形分析改进算法［J］.测试技术学报，2006，20（6）：543－548.

LI Guo-bin，GUAN De-lin.Vibration signals multifractal analysis improved algorithm［J］.Journal of Testing Technology，2006，20（6）：543－548.

［9］孙霞，傅竹西，吴自勤.薄膜生长的多重分形谱的计算［J］.计算物理，2001，18（3）：247－252.

SUN Xia，Fu Zhu-xi，WU Zi-qin.The calculation of multifractal spectrum of thin film growth［J］.Computational Physics，2001，18（3）：247－252.

［10］张亢，程军圣，杨宇.基于局部均值分解与形态学分形维数的滚动轴承故障诊断方法［J］.振动与冲击，2013，32（9）：90－94.

ZHANG Kang，CHENG Jun-sheng，YANG Yu.Roller bearing faultdiagnosis based on localmean decomposition and morphological fractal dimension［J］.Journal of Vibration and Shock，2013，32（9）：90－94.

［11］张锴锋，袁惠群，聂鹏.基于广义分形维数的刀具磨损状态监测［J］.振动与冲击，2014，33（1）：162－166.

ZHANG Kai-feng，YUAN Hui-qun，NIE Peng.Based on the generalized fractal dimension of toolwear conditionmonitoring ［J］.Journal of Vibration and Shock.2014，33（1）：162－166.

［12］李兆飞，柴毅，李华锋.多重分形的振动信号故障特征提取方法［J］.数据采集与处理，2013，28（1）：34－40.

LI Zhao-fei，CHAI Yi，LI Hua-feng.The multifractal fault feature extraction method of the vibration signals［J］.Data Acquisition and Processing，2013，28（1）：34－40.

［13］臧保将.一维信号序列的多重分形研究［D］.北京：北京交通大学，2006.1－48.

［14］周宇欢，张雄伟，付强，等.多分形谱簇研究及其在说话人识别中的应用［J］.信号处理，2011，27（12）：1914－1920.

ZHOU Yu-huan，ZHANG Xiong-wei，Fu Qiang al.Points form spectrum cluster research and its application in speaker recognition［J］.Signal Processing，2011，27（12）：1914－1920.

［15］李建毅，石林锁，滕明春，等.基于EMD和分形的齿轮箱故障特征提取［J］.陕西科技大学学报，2013，31（1）：115－121.

LI Jian-yi，SHI Lin-suo，TENG Ming-chun al.Based on EMD and fractal gearbox fault feature extraction［J］.Journal of shan xi University of Science and Technology of Signal Processing，2013，31（1）：115－121.

［16］朱云博，冯广斌，孙华刚，等.基于多重分形与SVM的齿轮箱故障诊断研究［J］.机械传动，2012，36（6）：99－102.

ZHU Yun-bo，FENG Guang-bin，SUN Hua-gang，et al.Gearbox fault diagnosis research based on multifractal and SVM［J］.Mechanical Transmission，2012，36（6）：99－102.

［17］李铁军，朱成实，吕营，等.基于概率神经网络的风机故障诊断［J］.煤矿机械，2007，28（10）：1－3.

LITie-jun，ZHU Cheng-shi，LÜYing，et al.The fan fault diagnosis based on probabilistic neural network［J］.Coal Mine Machinery，2007，28（10）：1－3.

Gear fault diagnosis based on multifractal theory and neural network

CHU Qing-qing，XIAO Han，LÜYong，YANG Zhi-wu
（MOE Key Laboratory of Metallurgical Equipment and Its Control，College of Machinery and Automation，Wuhan University of Science and Technology，Wuhan 430081，China）

Themechanical fault diagnosismethod based on themultifractal theory combined with the neural network was proposed according to multifractal characteristics of gear fault vibration signals.Themultifractal theory was used to calculatemultifractal spectra f（α）and generalized fractal dimensions D（q）of vibration time series.Taking the multifractal dimension spectral energy and the generalized fractal dimension spectral energy as characteristics，a twodimensional characteristic vector was formed，itwas taken as input parameters of a probabilistic neural network，and with it the fault classification for vibration signals collected from a gear fault platform was done.Experimental results showed that the proposed method can effectively be used in gear fault diagnosis，and it has a higher recognition rate.

multifractal theory；neural network；multifractal spectrum；generalized fractal dimension

TH133

A

10.13465／j.cnki.jvs.2015.21.003

国家自然科学基金项目（51105284）

2014－08－22 修改稿收到日期：2014－11－06

褚青青女，硕士生，1987年生

肖涵男，副教授，1979年生