主轴－刀柄联结性能有限元接触分析

蔡力钢，魏晓君，赵永胜，宋晓磊，杨 靖

（北京工业大学机械工程与应用电子技术学院，北京 100124）

主轴－刀柄联结性能有限元接触分析

蔡力钢，魏晓君，赵永胜，宋晓磊，杨 靖

（北京工业大学机械工程与应用电子技术学院，北京 100124）

主轴－刀柄联接系统是机床中最薄弱的环节之一，其联结性能是影响切削加工稳定性的关键因素。基于接触理论，考虑结合面间的法向作用和切向作用，建立了主轴－刀柄联结性能分析模型。分析了不同转速下刀柄锥面与主轴孔锥面的接触分离情况、刀柄锥面承受的接触压力和刀柄锥面的应力分布情况，得出了转速对主轴－刀柄结合面联接性能的影响规律。低转速时其联接性能稳定，而高转速时刀柄锥面与主轴孔锥面发生明显分离，刀柄接触压力下降到静止时的一半，刀柄应力显著增大，此时已无法保证两锥面紧密接触，主轴－刀柄联接性能丧失。最后通过高转速下主轴－刀柄系统径向加载试验验证了有限元接触分析的有效性与可行性，从而为进一步分析主轴－刀柄连接性能打下基础。

主轴－刀柄系统；接触分离；接触压力；刀柄应力

刀柄与主轴联结系统是机床中最薄弱的环节之一，联接性能直接影响和制约着加工的质量和效率。这方面的研究受到国内外学者的高度关注。在使用传统的非线性有限元方法研究中，Tsutsumi等［1－2］以实验和有限元仿真的方法，分析评估了HSK刀具系统的联接特性，Aoyama等［3］应用有限元仿真方法对比分析不同转速、不同径向力对HSK和BT刀柄结合部的径向刚度的影响，张松等［4］引入板接触单元分析刀柄－主轴结合面间的应力分布情况，董广强等［5］应用Ansys接触对单元对高转速下HSK工具系统的接触面压力进行了分析，李光辉等［6］分析了不同参数对刀柄－主轴联结性能的影响，路广等［7］分析了在过盈量、夹紧力、转速改变下对刀柄－主轴结合面的接触压力影响。

现有的应用有限元法进行刀柄－主轴联结性能的分析中，往往只考虑材料非线性和几何非线性，处理成一般的非线性有限元问题，而刀柄－主轴系统的关键在于相接触的两个锥面之间的结合效果。除了上述非线性外，还有边界条件非线性，即两个面的初始接触区域和状态是不确定的，并且随时间变化而变化，转速越高，这种非线性越强［8］。因此，一般的非线性有限元方法不能准确地反映接触面之间的实际情况，为此将接触理论应用于刀柄－主轴结合部的分析中。Hanna等［9］在分析HSK刀柄－主轴锥形结合部时引入了边界条件非线性，定义了刀柄－主轴锥面接触对以及接触面间的法向和切向相互作用，研究了锥形结合部的接触应力及锥面间隙量、连接刚度、最小夹紧力和刀柄内部应力分布情况。本文以7／24锥度的BT40刀柄为研究对象，基于接触理论建立了刀柄－主轴结合面的有限元模型，分析刀柄－主轴接触区域的接触压力分布、接触分离情况和刀柄应力分布，并进行分析比较，获得不同转速对刀柄－主轴联接性能的影响规律。

1 主轴－刀柄锥形面有限元接触建模

主轴－刀柄系统模型由刀柄和主轴组成，如图1所示。刀柄的锥面通过拉刀力实现与主轴孔锥面的紧密连接，主轴－刀柄锥形接触面是分析研究主轴－刀柄联结性能的关键。当刀柄通过拉刀力固定在主轴上时，主轴－刀柄结合面的初始接触区域和状态是不确定的，随着转速的不同，接触区域与接触状态会发生变化，即边界条件非线性，且转速越高，非线性越强。

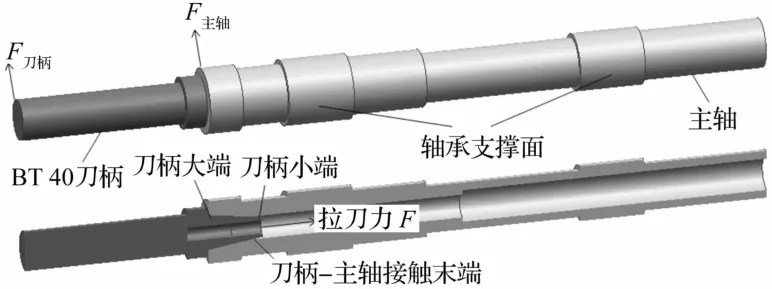
图1 BT40主轴－刀柄系统几何模型Fig.1 Geometricmodel of the spindle-toolholder system

根据接触理论，刀柄和主轴接触面之间的相互作用可以假设由两部分组成：一部分是接触面间的法向作用，另一部分是接触面间的切向作用。刀柄和主轴的材质同为20CrMo，刀柄锥面与主轴孔锥面之间不会彼此穿透，因此接触面间的法向作用可以不作任何限制，即采用“硬”接触模拟。对于切向作用，当主轴－刀柄接触表面发生接触时，在接触面之间会传递切向力和法向力。这样，在分析中就要考虑阻止两锥面之间相对滑动的摩擦力。应用库仑摩擦可以有效地描述接触面之间相互作用的摩擦模型，该模型应用摩擦因数μ来表征在两个表面之间的摩擦行为。库仑摩擦的计算公式为

式中，τ是临界切向力，μ是摩擦因数，p是法向接触压强。在切向力达到临界切应力时，接触面之间才会发生相对滑动［10］。只有当摩擦力对模型的响应有显著影响时才应该在模型中包含摩擦。主轴－刀柄系统在实际工作中两接触面是呈7∶24锥度的，在旋转过程中两接触面不仅有法向的相互作用，也会有切向相互作用，即产生摩擦力，因而定义一个恰当的摩擦因数是必要的。根据工程经验，摩擦系数一般取0.05～0.2。本模型中使用一个允许“弹性滑动”的罚摩擦公式并设定摩擦因数0.1。

由于两接触面间的接触状态在高速转动过程中不断地变化，需要在接触计算过程中不断地判定从面节点和主面的哪一部分发生接触，因而用有限滑移来描述两接触面间的相对滑动特性。此外由于在建模过程中尺寸误差的影响，需要定义一个0.1mm的位置误差限度，确保主轴－刀柄锥面在仿真开始时保持接触，如图2所示。

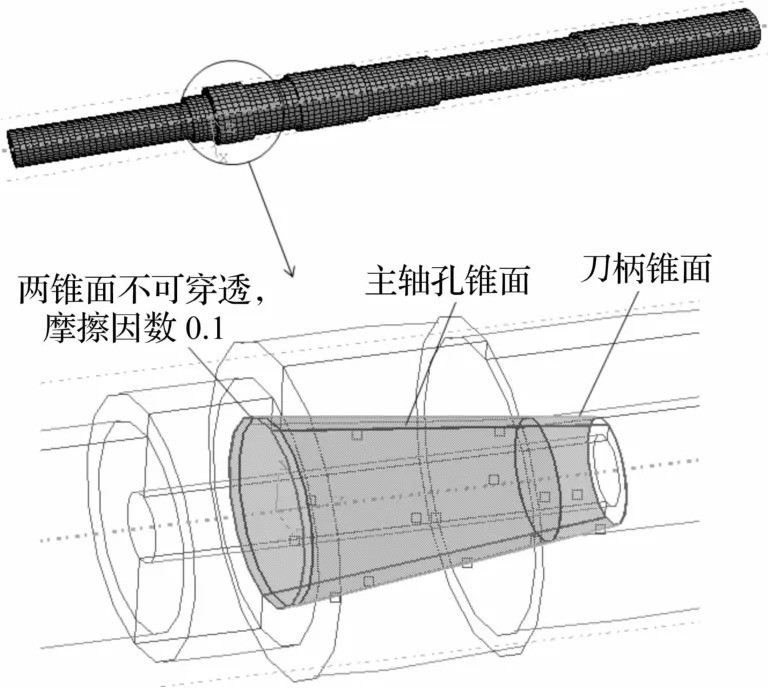
图2 BT40主轴－刀柄系统有限元模型及锥面接触对Fig.2 Finite elementmodel of BT40 spindle-toolholder system and the taper-to-taper contacts

主轴－刀柄系统中，装配后质心与回转中心并不一致，即不平衡量。不平衡量可用克×毫米（g·mm）表示。平衡等级G允许的不平衡量U的计算公式为：

式中，m为回转物体的质量（kg），n为主轴转速（r／min）。其中平衡等级G取决于加工要求。主轴的平衡等级取高速加工机床的平衡等级2.5，普通BT40刀柄的平衡等级为2.5。以25 000转时为例，刀柄允许的不平衡量为：

2 接触仿真分析

在刀柄－主轴系统模型中，将主轴拉刀力设置为工程中推荐的12 kN，分析从静止到30×103r／min时刀柄－主轴锥面接触分离情况、刀柄锥面接触压力分布和刀柄应力分布情况以及刀柄受力径向变形量。

2.1 刀柄－主轴锥面接触分离分析

图3所示为0～30×103r／min转速下刀柄－主轴锥面接触间隙，图中横坐标表示沿刀柄锥面从大端到小端的距离。由分析结果可知：25×103r／min为临界转速，小于该转速时锥面接触间隙始终为负值，表明刀柄锥面与主轴孔锥面之间始终是保持接触状态。当转速达到30×103r／min时，10 mm、14 mm和17 mm处接触间隙量分别为0.05μm、0.032μm和0.04μm，即两锥面在这一区域分离。以上分析说明转速在25×103r／min以下时刀柄－主轴锥面可以保证接触，当转速达到25×103r／min时即有分离趋势，达到30×103r／min时出现较明显分离，且分离出现在锥面大端到锥面20 mm范围内。值得注意的是，25×103r／min以下虽然可以保证锥面接触，但锥面间承受的接触压力不足以保证锥面紧密接触，2.2节将通过分析刀柄－主轴锥面接触压力，判断保证锥面紧密接触的临界转速。

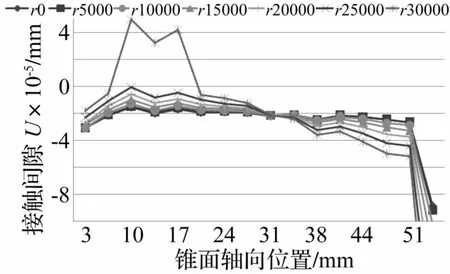
图3 静止及六种转速下刀柄－主轴锥面接触间隙曲线Fig.3 Curves of the taper-to-taper contact gaps at static and six kinds of rotational speeds

2.2 刀柄锥面接触压力分析

刀柄在静止及六种转速情况下锥面接触压力分布规律相似，即沿刀柄轴向呈区域圆环状分布。接触压力从接触末端沿着轴向方向向刀柄大端逐渐减小，其中最大接触压力出现在刀柄锥面与主轴孔锥面接触的末端。

由于现有实验方法无法获得高转速情况下结合部的真实接触状态，因而仿真分析得到越来越多的应用。图4反映了锥面接触压力在静止及低速（5×103r／min 和10×103r／min）和高速（15×103r／min及以上）时的仿真分布情况，可以看出10 mm、14 mm和17 mm三点处是整个刀柄锥面上接触压力最小的区域。结合2.1节的分析可知，刀柄－主轴锥面在10mm、14mm和17 mm三点处的接触间隙最大，即这一区域发生接触分离的可能性最高，因而需要重点分析这一区域的接触压力。而这一结果与之前学者获得的结合部大端出现“喇叭口”现象十分吻合，也反应了仿真结果的真实与可靠性。

从表1可以看出，零转速时这三点的接触压力分别为5.96 MPa、6.7 MPa和6.21 MPa，此时可以保证锥面紧密接触（拉刀力使刀柄紧紧连接到主轴上）。5× 103r／min和10×103r／min时，这一区域的接触压力始终保持在5 MPa以上，下降幅度最大的是10×103r／min时10 mm处，为14.5%。当转速达到15×103r／min时，10 mm处下降了31.9%，20×103r／min时这一区域的接触压力下降了一半左右，25×103r／min和30×103r／min时锥面已基本分离。从图4还可以看出，在锥面接触末端位置（55 mm），随着转速的提高，接触压力在不断地增大，15×103r／min时已达到34MPa，而30 000转时则达到62 MPa。刀柄－主轴系统在高速转动状态下结合部大端的径向变形明显高于小端，因而刀柄与主轴接触部位更加靠近刀柄小端，接触压力相应增加。接触末端位置的接触压力过高会导致即使刀尖承受很小的外力，也会造成结合部接触面积减小，刀柄会产生很大的振动，进而影响了接触性能和切削质量。

刀柄－主轴系统联接是靠两锥面紧密接触实现的，当锥面接触压力下降过大时就无法保证锥面可靠联接。当转速达到20×103r／min时，锥面大端位置（10 mm、14 mm和17 mm三点处）接触压力下降一半，因而已无法保证两锥面紧密接触，转速高于20 000转时则已基本丧失联接。

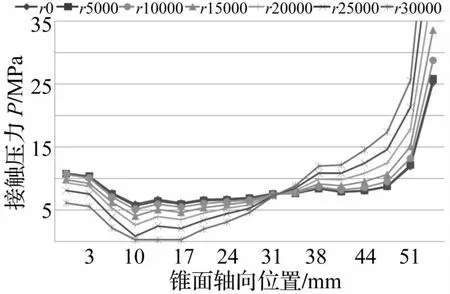
图4 静止及六种转速下刀柄锥面接触压力曲线Fig.4 Curves of taper-to-taper contact pressures in the toolholder at static and six kinds of rotational speeds

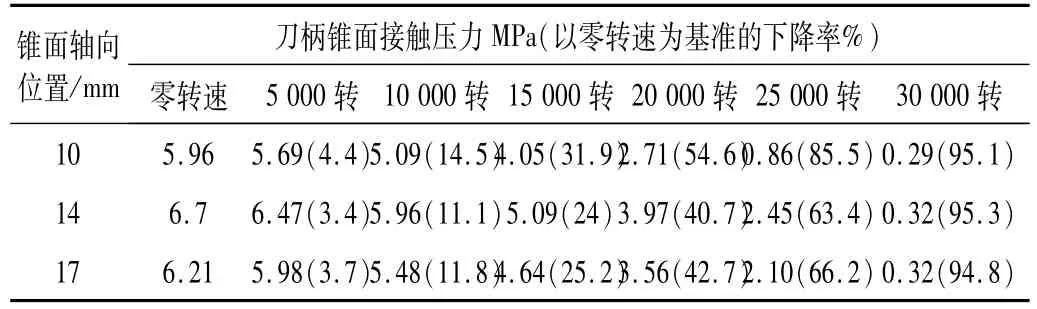
表1 BT40刀柄锥面10mm、14mm 和17mm三点处接触压力值及下降率Tab.1 Taper-to-taper contact pressures and rates of decline for three points in BT40 toolholder（10mm，14mm，17mm）

2.3 刀柄应力分析

应力分布可以反映出刀柄在工作时各个位置应力大小以及最大最小应力区域，得出刀柄在实际使用中最脆弱的位置。BT40刀柄静止及六种转速下应力分布曲线如图5所示。由图可知，静止时刀柄应力从大端开始逐渐增大，在锥面接触末端位置应力值达到最大，接着应力值略微下降，在拉刀力施加处应力又有所增大。5×103r／min和10×103r／min时应力曲线与静止时基本保持一致。15×103r／min时应力曲线发生改变，在10mm处出现了应力最小值，然后才逐步增大。因此，可以得出15×103r／min是刀柄－主轴系统的一个关键转速，同时也反映出转速对结合部的重要影响。随着转速的继续提高，应力最小值出现的位置向刀柄小端移动，20×103r／min时出现在14 mm处，25×103r／min时出现在20mm处，30×103r／min时出现在28 mm处。

从以上分析可以发现，静止及低速（5×103r／min 和10×103r／min）时应力分布呈现一种规律，但在高速时分布规律发生改变，应力最小值出现的位置不断向刀柄小端移动，这说明刀柄应力分布受转速影响较大，高速时呈现出新的规律，需要不断深入研究。

另一方面，静止及低速时刀柄最大应力区域为锥面接触末端和拉刀力施加位置，高速时锥面接触末端的应力不断增高，拉刀力施加位置应力略微降低。因此，在静止及低速时锥面接触末端与拉刀力施加位置出现应力集中，随着转速的提高，锥面接触末端的应力集中更为明显，在实际使用中需要注意。

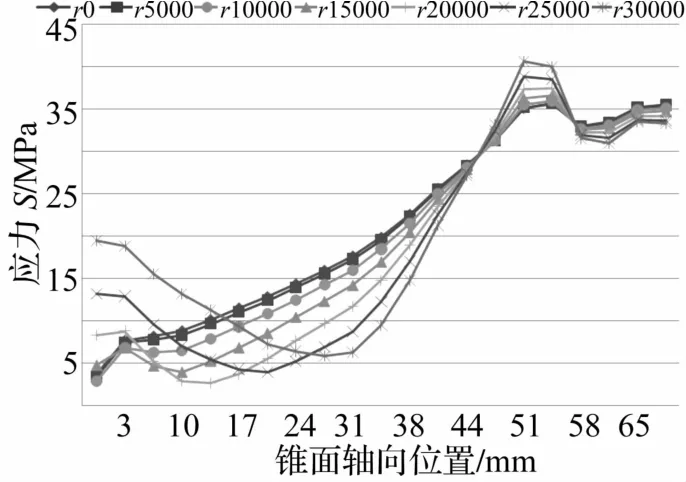
图5 BT40刀柄静止及六种转速下应力对比图Tab.5 Comparison ofstresses in BT40 toolholder at static and six kinds of rotational speeds

2.4 刀柄受力时径向变形分析

基于上述BT40刀柄－主轴有限元接触模型，在刀柄外圆柱面末端处施加45N的径向力，模拟刀柄实际加工时的切削力，计算了六种转速下刀柄的径向变形量，结果列于表2。表2反映出随着转速的提高，刀柄径向变形量逐渐增大。

表2 刀柄径向变形仿真值Tab.2 Simulation values of the toolholder's radial deformation

锥面接触分离和接触压力是反映刀柄－主轴锥形结合部联接性能的关键因素。这两个因素是相互关联的：当接触未分离时，接触压力为正；当接触分离时，接触压力为零或略大于零。刀柄应力是反映刀柄实际使用性能的重要参数，刀柄锥面区域的应力分布与锥面接触压力分布规律相似。

静止及低速时刀柄－主轴锥面未分离，接触压力比较大，从而保证两锥面可靠联接；由于其结构特点，在锥面接触末端及拉刀力施加位置均出现应力集中现象。当转速达到20×103r／min以上时两锥面发生大面积分离，接触压力下降到接近于零的水平，锥面联接明显失效；而锥面接触末端及拉刀力施加位置的应力集中更加剧烈，极易发生疲劳磨损。对比静止及低速时与高速时的结果可知，高速时刀柄－主轴锥形结合部的联接性能急剧下降。普通BT刀柄应该尽量避免高速高精的加工场合。

3 实验验证

研究BT40刀柄在安装模拟偏心刀具的情况下，以不同转速旋转时刀柄受力变形。具体实施方式为：将一根长49 mm，直径6 mm的刀杆插到模拟偏载板的φ6圆孔中，焊接形成模拟偏载刀具，如图6所示。其中模拟偏载板为对称结构，除了中间安装刀杆的圆孔外，左右各有9个M3的螺纹孔，用来安装螺钉。通过螺钉的不同组合，可以模拟旋转时不同大小的径向力（离心力）。

每根螺钉的质量约为0.8 g。根据模拟刀具板上螺纹孔的位置以及螺钉安装个数的不同，模拟偏载可模拟不同大小的离心力。将模拟偏载刀具安装到BT40刀柄上，在高速旋转时可通过不同的偏心位置、质量计算出旋转状态下所受的偏心力，并利用激光测振仪以及LMS工具测量刀柄的振动量。图7所示为旋转状态下刀柄径向变形测量图。

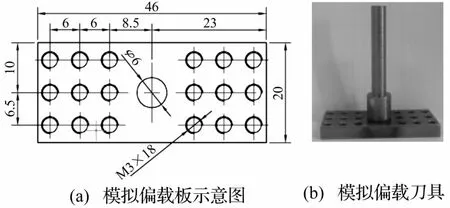
图6 模拟偏载板示意图与模拟偏载刀具Fig.6 Sketch of the board used to simulate unbalance load and the tool used to simulate unbalance load

图7 旋转状态下刀柄径向变形测量图Fig.7Way ofmeasuring radial deformation of the toolholder inthe state of spindle's rotating

在实验验证刀柄受力变形的过程中，当转速超过20×103r／min时机床已出现明显振动，这对刀柄变形量的测量具有很大影响，因而实验测量了5×103r／min 到20×103r／min四种转速下刀柄的径向变形量。通过调整螺钉的位置，设定模拟偏载力为45N，实验结果列于表3，实验值与仿真值无量纲对比如图8所示。

图8 刀柄径向变形量实验值与仿真值无量纲对比Fig.8 Comparison of dimensionless experimental results andsimulation values of the toolholder's radial deformation

5×103r／min时实验值为3.38μm，仿真值为2.62 μm，偏差22.5%；10×103r／min时实验值3.51μm，仿真值2.71μm，偏差22.8%；15×103r／min时实验值3.85μm，仿真值2.86μm，偏差25.7%；20×103r／min时实验值4.3μm，仿真值3.06μm，偏差28.8%。偏差30%以内。产生这种结果的原因可能是低速时机床本身的振动量较小，对激光测振仪测得的数据影响较小，而当转速提高时，实验测量的刀柄变形量包括了较多机床振动量，加上由于计算产生的误差，致使实验值与仿真值的偏差变大。

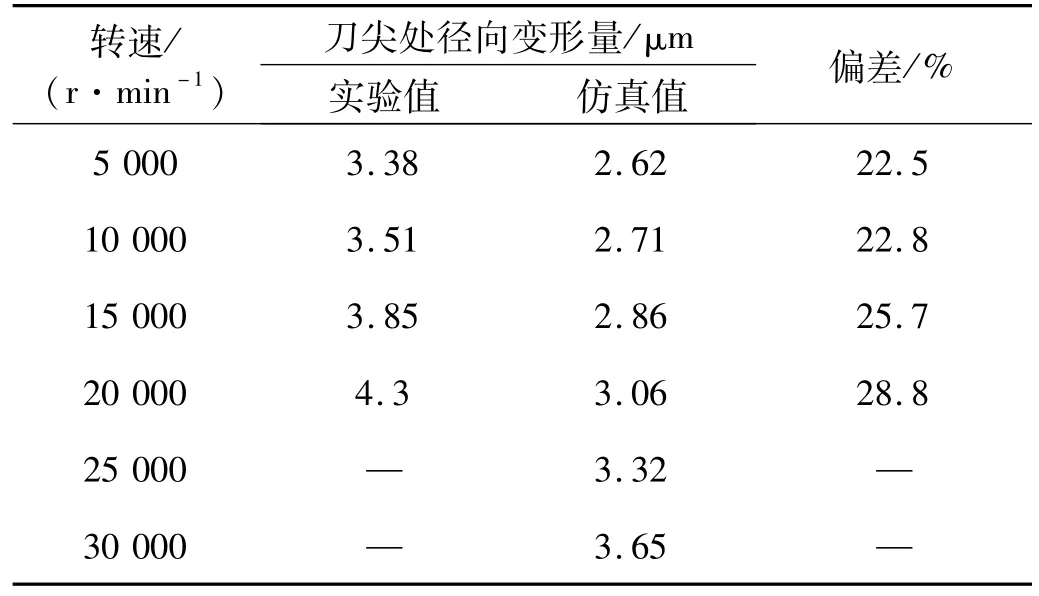
表3 刀柄径向变形量Tab.3 Radial deformation of the toolholder

为了更加清楚地比较实验与仿真的结果，对两者分别进行了无量纲化，即实验值与仿真值分别除以5× 103r／min时的数值，得到的图形如图8所示。从图中可以看出实验值与仿真值是有差别的，两者的差值可能是机床本身振动造成的，但从总体规律来看，两者都随转速的提高而增大，并且呈现相同的增长规律，这验证了仿真结果与实验结果相吻合。

4 结 论

（1）BT刀柄－主轴系统在低转速情况下，其锥面结合情况较好；而在转速达到20×103r／min时，尽管刀柄锥面与主轴孔锥面还未发生分离，但接触压力已经下降了一半，已不能保证锥面紧密接触；当转速继续提高，接触分离范围扩大，接触失效。

（2）刀柄应力分布也受转速的影响。低转速情况下，从刀柄大端到小端应力值逐渐增加；但是在高速情况下，结合部的性能完全不同于低速，应力分布呈现出新的规律，即应力最小值出现的位置不断向刀柄小端移动，说明转速对结合部接触性能的影响十分明显。

（3）通过对刀柄受力径向变形的实验测量，验证了有限元分析的可靠性。

［1］Tsutsumi M，Ohya M，Aoyama T，et al.Deformation and interface pressure distribution of 1－10 tapered joints at high rotation speed［J］.Journal of Japan Society for Precision Engineering，1996，30（1）：23－28.

［2］TsutsumiM，Kuwada T，Shimizu S，etal.Static and dynamic stiffness of 1－10 tapered joints for automatic changing［J］.Journal of Japan Society for Precision Engineering，1995，29 （4）：301－306.

［3］Aoyama T，Inasaki I.Performances of HSK tool interfaces under high rotational speed［J］.Annals of the CIRP，2001，50（1）：281－284.

［4］张松，艾兴，刘战强，等.7∶24主轴／刀柄联接非均匀应力场的有限元分析［J］.工具技术，2003，7：25－27.ZHANG Song，AIXing，LIU Zhan-qiang，etal.FEA of nonuniform stress fields on 7∶24 spindle／toolh older interfaces ［J］.Tool Engineering，2003，7：25－27.

［5］董广强，王贵成，王树林，等.高速加工中HSK工具系统精度的研究［J］.中国机械工程，2005，16（24）：2179－2183.DONG Guang-qiang，WANG Gui-cheng，WANG Shu-lin，et al.Research on precision of HSK tool systems in high speed machining［J］.Chinese Journal of Mechanical Engineering，2005，16（24）：2179－2183.

［6］李光辉，冯平法.HSK刀柄与主轴联结性能的有限元分析［J］.工具技术，2005，39（9）：27－30.LIGuang-hui，FENGPing-fa.Finite elementanalysis of HSK toolholder and spindle interface［J］.Tool Engineering，2005，39（9）：27－30.

［7］路广，吴勇中，桂贵生，等.HSK刀柄／主轴联接性能分析［J］.制造技术与机床，2009（2）：37－40.

LU Guang，WU Yong-zhong，GUIGui-sheng，et al.Analysis on HSK tool-holder／spindle interface［J］.Manufacturing Technology＆Machine Tool，2009（2）：37－40.

［8］程强，宋晓磊，蔡力钢，等.刀柄－主轴系统联结性能有限元接触分析［J］.计算机集成制造系统，2012，18（4）：775－780.

CHENG Qiang，SONG Xiao-lei，CAILi-gang，et al.Contact finite element analysis on performances of spindle／toolholder connection［J］.Computer Integrated Manufacturing System，2012，18（4）：775－780.

［9］Hanna IM，Agapiou J S，Stephenson D A.Modeling the HSK toolholder-spindle interface［J］.ASME Journal of Manufacturing Science and Engineering，2002，124（8）：734 －744.

［10］庄茁，由小川，等.基于ABAQUS的有限元分析和应用［M］.北京：清华大学出版社，2009：287－290.

Contact finite element simulation for Spind le／toolholder connection performances

CAILi-gang，WEIXiao-jun，ZHAO Yong-sheng，SONG Xiao-lei，YANG Jing

（College of Mechanical Engineering and Applied Electronic Technology，Beijing University of Technology，Beijing 100124，China）

A spindle／toolholder connection system is one of the weakest sections in amachine tool.The quality of machining is related to its connection performance.Here，amodel of the spindle／toolholder system was established based on the contact finite element theory.Normal direction and tangential one actions between interfaceswere considered.The taper-to-taper clearances，the taper-to-taper contact pressure and the stress of the toolholder at different rotating speeds were analyzed.Itwas shown that under static and low speed conditions，its connection performances are stable；however，when the rotating speed is high，the tapers of the tool holder and the spindle hole are departed，and their contact pressure is only half of that under the static condition，and the stress of the toolholder grows significantly at the same time，the connection performances getworse.Finally，tests verified the reliability of the analysis.

spindle／toolholder connection；clearances；contact pressures；stress

TG506

A

10.13465／j.cnki.jvs.2015.21.002

国家自然科学基金（51375025）

2014－07－17 修改稿收到日期：2014－09－16

蔡力钢男，博士，教授，博士生导师，1958年6月生

魏晓君男，硕士生，1987年5月生