看最新高考试题 谈数列求和方法

石家庄二中实验学校 李姗姗

数列是高中数学比较重要的一个知识版块，课程标准中要求教师用大约12课时进行教学；在每年的高考试题中，不论是选择或填空对基础知识、基本解题方法的考查，还是解答题中与其他知识交汇命题综合考查都会涉及数列的知识，由此可见数列在高考中的地位实在是不一般。本文就解答题中最常见的一类问题——求数列的前n项和问题，结合最新高考试题对其常用解法加以分析。

一、公式法

公式法，指的是在已知数列是特殊的等差（等比）数列时，可以直接利用所学的等差（等比）数列的求和公式求解前n项和。

例1（2014年浙江卷·文）已知等差数列{an}的公差d>0，设{an}的前n项和为

（1）求 d及 Sn；

（2）求 m，k（m，k∈N*）的值，使得

（a1+a2）（a1+a2+a3）=36，

即（2+d）（3+3d）=36，

化为d2+3d-10=0，

解得d=2或-5，

又公差d>0，则d=2，

（2）由（1）得，an=1+2（n-1）=2n-1，

由am+am+1+am+2+…+am+k=65得，

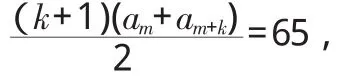
即（k+1）（2m+k-1）=65.

又 m，k∈N*，则（k+1）（2m+k-1）=5×13，或（k+1）（2m+k-1）=1×65，

下面分类求解：

当 k+1=5时，2m+k-1=13，

解得 k=4，m=5；

当 k+1=13时，2m+k-1=5，

解得 k=12，m=-3，故舍去；

当k+1=1时，2m+k-1=65，

解得k=0，故舍去；

当k+1=65时，2m+k-1=1，

解得 k=64，m=-31，故舍去；

综上得，k=4，m=5.

二、倒序相加法

在推导等差数列前n项和公式时用到的就是“倒序相加法”，这种方法适用的数列要具有以下特点：数列的首末两端等“距离”的两项的和相等。

三、错位相减法

该方法是推导等比数列前n项和时用到的方法，也是高考中考查频率最高的一种求和方法。这种方法适用于所求数列的各项是一个等差数列和一个等比数列的对应项之积的情况。使用该方法时一定要注意在两端同时除以某项时，前提条件是该项永远不为0，在直接利用等比数列的前n项和公式时也要特别注意。

例2（2014年江西卷·理）已知首项都是 1的两个数列 {an}，{bn}（bn≠0，n∈N+），满足 anbn+1-an+1bn+2bn+1bn=0.

（1）令，求数列{cn}的通项公式；

（2）若 bn=3n-1，求数列{an}的前 n 项和 Sn.

解：（1）因为 anbn＋1－an＋1bn＋2bn＋1bn＝0，bn≠0(n∈N*)，

即 cn＋1－cn＝2，

所以数列{cn}是以c1＝1为首项，d＝2为公差的等差数列，故cn＝2n－1.

（2）由 bn＝3n－1，知 an＝(2n－1)3n－1，

于是数列{an}的前n项和

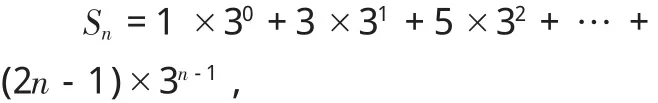
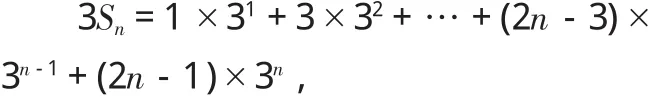
将两式相减得：

所以 Sn＝(n－1)3n＋1.

四、分组求和法

当一个数列的通项是由明显的等差与等比构成的时候，可以采用此种方法，将数列的项重新分组，分别利用等差（等比）数列的前n项和公式求和后再相加。

例3（2014年湖南卷·文）已知数列{an}的前n项和

（1）求数列{an}的通项公式；

（2）设 bn=2an+（-1）nan，求数列{bn}的前2n项和.

解：（1）当 n＝1时，a1＝S1＝1；

当n≥2时，

故数列{an}的通项公式为an＝n.

（2）由(1)知，bn＝2n＋(－1)nn.

记数列{bn}的前2n项和为T2n，

则 T2n＝(21＋22＋…＋22n)＋(－1＋2－3＋4－…＋2n)．

记 A＝21＋22＋…＋22n，

故数列{bn}的前2n项和：

数列求和问题一般出现在解答题的后一问，在求出数列的通项公式之后，设置利用通项公式构造的新数列的求和问题，形式虽然各有不同，但是求和方法不外乎以上几种。只要认真领会上述几种求和方法的要领，认真分析数列前n项和形式的特点，“对症下药”，选对方法，解决这类问题不在话下。