基于线性调整的运筹统计量算法

李长国，索文莉，钟 敏，刘艳娜

(军事交通学院基础部，天津300161)

存货问题(也称为报童问题)是指在面临未来不确定的需求时，如何确定存储货物的数量问题。如果现有的存货小于未来的需求，就会发生供不应求的遗憾损失;相反，如果现有的存货大于未来需求，则发生供大于求的剩余损失。所以要在其中确定基于某种法则的最优存货量，使得发生损失的数量尽可能小。

存货问题已经得到大量研究，一般是用概率分布来描述未来的需求。在分布完全已知时，不难得到最优的存储策略。但由于分布往往未知，或者形式已知但存在未知参数，所以要由过去的数据估计。而由估计参数确定的最优存储策略，存在评价目标函数的调整，以及由此带来的优化问题。文献［1］给出一个指数分布、样本数量相对较少条件下，常规估计量对应的目标函数并非最优的问题。本文假设需求服从某个分布族，借助文献［1］的思想将参数估计和收益最大的目标结合起来，给出了一种新的估计思路，该方法能够适应更一般的需求分布。

1 存货问题的优化模型

在报童问题中，设商品的买进价格为c，卖出价格为s，剩余商品没有回收价值。在需求量为d、进货量为x时的收益为Φ(x，d)=s min{d，x}－cx。实际问题中，往往设需求量d为一个随机变量，设其分布函数为Fd(d;θ)，则期望收益为

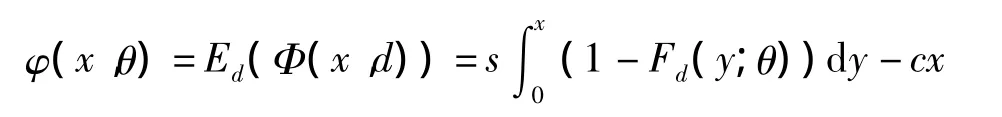
存货控制的目标是确定存货量x，使得期望收益 φ(x，θ)最 大。在 φ(x，θ)可微 条 件 下，φ＇(x，θ)=s(1 － Fd(x;θ))－ c。考虑 φ＇(x，θ)的零点所在的位置，最优存货量(optimal order quantity，OOQ)为

将 x(θ)代入 φ(x，θ)得到期望最优收益(optimal expected profit，OEP)为

当需求d服从单参数指数分布时，其具有分布函数 F(x，θ)=1 －e－x/θ，算得 OOQ 和 OEP 分别为

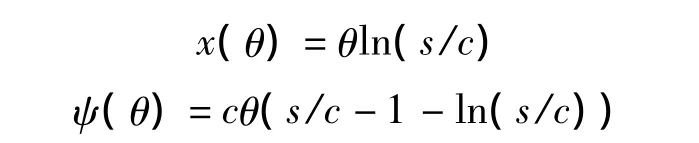
当参数θ未知时，往往借助观测样本˜d=(d1，d2，…，dn)估计θ。设估计量为^θ，则OOQ的一个自然的估计量为x(^θ)。然而这种替代思想得到的估计量并非使期望收益函数(a priori expected profit，APEP)最大的存货量。例如文献［1］指出，在指数需求分布条件下，OOQ的估计量为x(^θ)=(s/c)≐^xsm，对应的APEP为

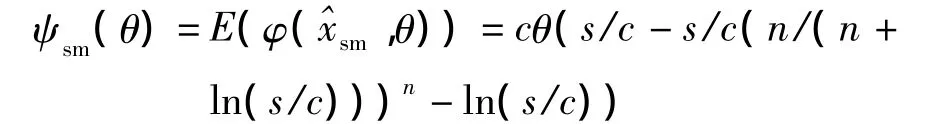
而订货量为 ^xos=n((s/c)1/(n+1)－1)¯d，对应的APEP为容易验证 ψsm(θ)＜ ψos(θ)＜ ψ(θ)。

2 未知需求分布条件下最优存货量的求解

在设计最优存货量时，文献［1］引进了控制变量z，并调整存货估计量x(^θ)为^x(z)=zx(^θ)，以此作为最优存货量的备选量。这样由原来极大化E(φ(x(^θ)，θ))的函数优化问题，简化为极大化Ε(φ(^x(z)，θ))的参量优化问题。当需求服从指数分布时，最优解恰为=n((s/c)1/(n+1)－1)而对于其他分布，由于没有存货量的解析表达式，要涉及到数值计算，文献［1］没有进一步讨论这个问题。

文献［2］从贝叶斯角度，理论上给出任意分布条件下最优解的表达式:

利用这个结果，文献［2］不但证明了文献［1］的结果为最优存货量，而且在均匀分布时的最优存货量的表达式:

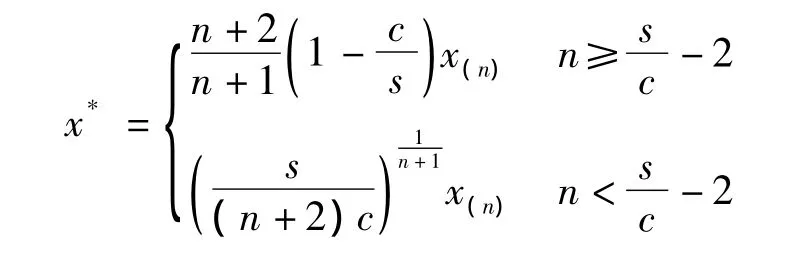
但利用式(1)很难计算其他分布的存货量。尽管文献［2］也给出两个参数的需求分布情况下的存货量的理论计算公式，但由于计算上的困难而很难计算其他分布的最优存货量。

针对一般分布下，最优存货量大多采用数值计算方式获得，文献［3］考虑了线性纠偏的计算思路:首先确定未知参数的可能参考区间{θi:i=1，2，…，r}(r称为空间容量)，这主要通过经验或者样本估计得到;再由这些参考参数得到最优存货量列{xi=x(θi):i=1，2，…，r}，进而得到 APEP 列{φ(xi，θi):i=1，2，…，r};从参考参数 θi出发模拟来自分布F(x;θi)的样本，构造参数的估计量^θi，得到订货量^xi=^x(^θi);最后，线性纠偏为β^xi，得到相应收益列φ(β^xi，^θi)，再最小化目标:

这个调整的目标是寻找β使得φ(βx(^θ)，^θ)尽可能接近真实的φ(x(θ)，θ)，但这个最优解并非使Ε(φ(βx(^θ)，θ))最大的订货量。所以目标函数可以调整为

另一方面，最优参数c不但和样本量n有关，也是空间容量r的函数，所以最终的参数应表示为

具体执行时，对于每个θi，采用蒙特卡洛法模拟m组来自分布F(d，θi)的样本，从而得到m个θi估计量^θij，j=1，2，…，m，从而得到优化函数为

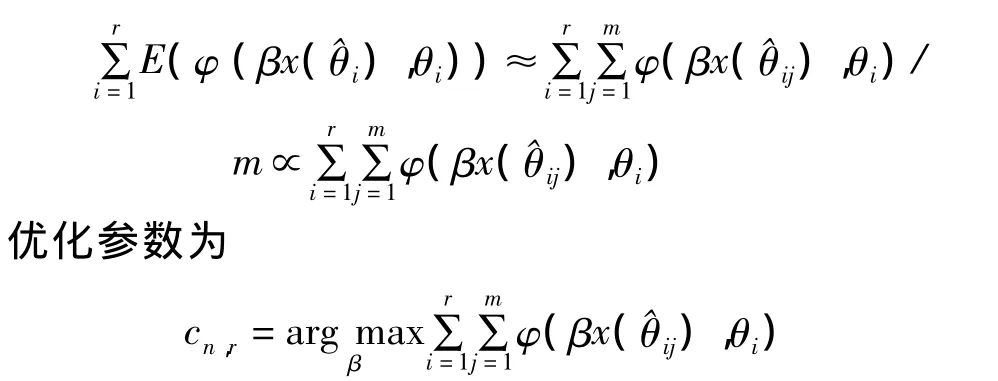
模拟中取较大 r，直到 cn，r稳定为止。实践中可以尝试不同的空间容量r导致的最优调整系数cn，r，通过两两比较方法确定参数 r。具体地，对于需求分布为指数分布，当进货价格和零售价分别为 c=1、s=1.2 时，样本容量为 n=4，调整系数假设可能的调整范围为0.5～1.5。以 r=40为基准，模拟30次得到一列最优调整系数，将空间容量取5～40，得到的各列调整系数分别与基准r=40得到的最优系数做两两比较，得到一列检验p值。查看这些p值的散点图，寻找比较稳定p值，其对应的空间容量r作为合适的容量。如图1所示，检验p值在参数空间容量r(大于10之后)没有显著的变化趋势，所以我们模拟中采用的容量为r=10。

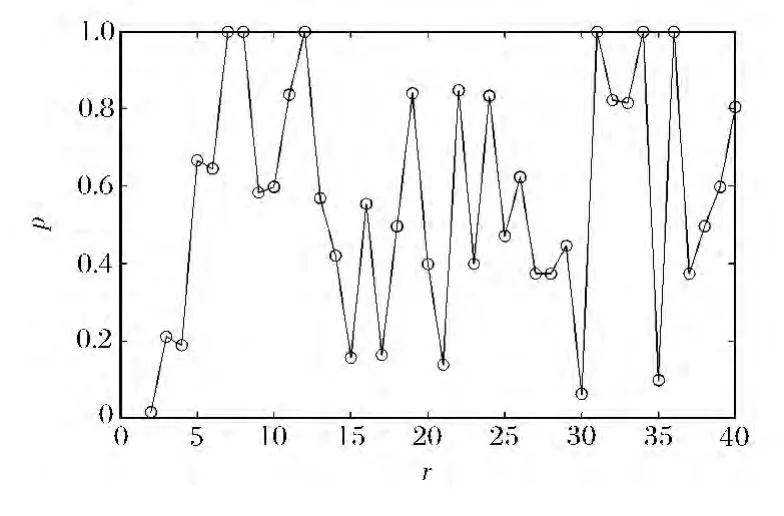
图1 指数分布中参数空间的p值散点

因此，在需求分布F(d;θ)参数θ未知、但有样本 ˜d=(d1，d2，…，dn)条件下，确定调整系数和最优订货量的线性调整算法(linear correction，LC)的步骤如下。

(1)确定期望收益函数和最优存货量。根据需求分布F(x;θ)、成本c和售价s，确定期望收益函数:

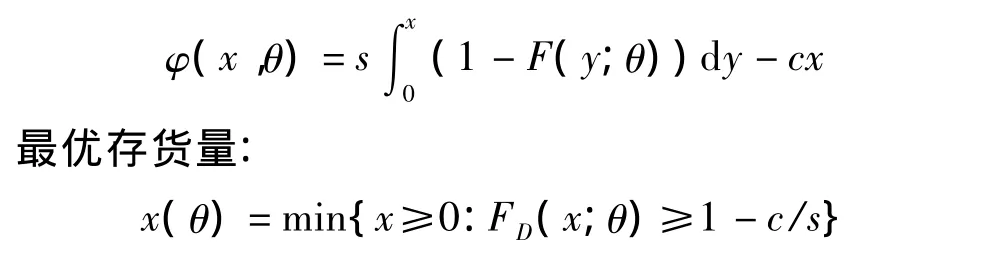
如果没有解析式，给出数值解。

(2)模拟存货量和期望收益列。根据历史观测或者经验，确定参数θ的可能范围，确立参考向量 θa=(θi:i=1，2，…，r)。对于每个 θi，模拟 m 组来自分布F(d，θi)的样本，从而得到 m个估计量”^θij，j=1，2，…，m，以及m个存货量的“估计量”x(^θij)。再将x(^θij)调整为βx(^θij)，进而形成m个期望收益列φ(βx(^θij)，j=1，2，…，m)。

从而得到最优存货量cnx(^θ)，其中^θ为θ的估计量。

3 算法验证

3.1 指数需求分布

当需求为指数分布，即F(x;θ)=1－exp(－x/θ)时，期望收益和最优存货量分别为

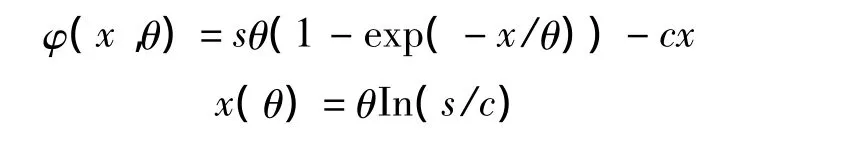
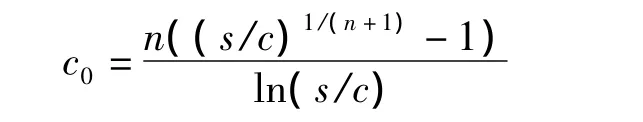
这是检验LC算法合理性的依据。表1为文献［3］和LC方法的模拟对比结果。结果说明在指数需求时，由LC方法确定的存货量是合理的，而文献［3］的纠偏方法不但偏差大，而且不稳定。

表1 指数分布两种调整方法对应的调整值

3.2 均匀需求分布

需求分布为均匀分布时，即 F(x;θ)=x/θ，x∈(0，θ)期望收益为

最优存货量为 x(θ)=(s－c)θ/s。当参数 θ未知时，最优存货量的估计量^x=cnx(^θ)=cn(s－c)×x(n)/s。文献［2］给出的存货量为

这是检验算法合理性的依据。均匀分布时文献［3］和LC方法的模拟对比结果见表2。

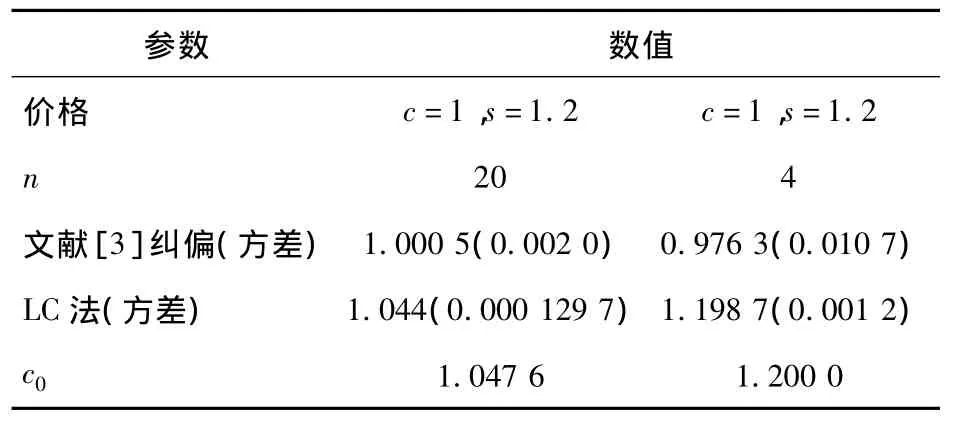
表2 均匀分布两种调整方法对应的调整值

4 案例分析

以某一报亭为例，经验知道该报亭的某报纸每天销量服从指数分布(参数为50份)。该报纸每份进价为c=0.1元，售价为s=0.5元。订货策略为根据上个周期的4个数据 d1、d2、d3、d4确定下个周期的库存量。我们分别使用替代法和纠偏法计算平均利润，比较两个利润的大小。其中替代法对应的订货量为x(^θ)=¯dln(s/c)，纠偏法对应的订货量为^x=cn¯dln(s/c)，其中 cn=0.943 9。通过随机模拟，得到两个进货对应的每周利润差为0.043 元。

5 结语

使用线性纠偏的方法计算得到的最优存货量方法，不但得到覆盖了现有文献的结果，也适用于较为复杂的分布情形。对于离散分布和高维分布的需求情况，考虑到篇幅原因，本文没有给出具体的计算过程，留待进一步研究。

［1］ Liyanage L H，Shanthikumar J G.A practical inventory control policy using operational statistics［J］.Operational Research Letter，2005(33):341-348.

［2］ Chu L Y，Shanthikumar J G，Shen Z M.Solving operational statistics via a bayesian analysis［J］.Operational Research Letter，2008(36):110-116.

［3］ Ramamurthy V，Shanthikumar J G.Inventory policy with parametric demand:operational statistics，linear correction，and regression［J］.Production and Operations Management Society，2012(21):291-308.