大规模作战物流配送VRP模型及求解

张 锦，聂 伟，沈 军，谢小平

(镇江船艇学院动力指挥系，江苏镇江212003)

随着以信息化为核心的新军事变革的深入推进，基于信息系统体系作战的战斗力生成模式正在加速转型。作为军队作战“生命线”和后勤保障中心环节的军交运输，在战争中的地位和作用将更显突出，甚至直接制约着战争的进程和结局。配送是军事物流的重要环节，是将后勤保障物资转化为作战能力的纽带，肩负着将作战物资交付到作战部队的重要任务，其路径的优化选择对军交运输效率有着重要影响。交战双方的较量，不仅是武器装备的较量，也是军事物流配送力量的较量，哪一方能得到高质量的军事物流支持和保障，哪一方便获得了军事行动的主动权［1］。

按照运输任务样式的不同，大规模作战物流配送问题可分为多式联运问题和车辆路径问题:由后方物流中心或战略仓库向前方配送中心或部队用户的配送一般属于长距离运输，需要综合运用多种运输方式，属于多式联运;由前方配送中心向各部队用户的配送一般属于车辆路径问题。这里的车辆是广义概念，可以是汽车、船艇、飞机等。大规模作战需要保障的部队用户众多，配送方案决策复杂，需要通过建立数学模型，运用计算机求解的方法来制订快速、精确、安全、高效的配送方案。车辆路径问题(vehicle routing problem，VRP)最先由Dantzig和Ramser于1959年提出，经过半个多世纪的深化和扩展，国内外学者针对不同领域应用衍生出不同类型的VRP:按照信息(包括客户需求、车辆信息和路况信息等)是否确定可大致分为不确定性VRP和确定性VRP［2－4］。根据军事物流配送中VRP的特点，本文将重点针对确定VRP中的单/多配送中心、单/多车型、装卸一体、带时间窗的VRP开展研究。

1 问题描述及约束条件

车辆路径问题是车辆装载物资由前方配送中心出发，对配送网中的部队用户进行保障，然后返回配送中心的过程。配送网 G(V，E，S，T，C，P)中:V为点集，总数为n，vi∈V为配送网中的点，包括配送中心和部队用户;E为边集，eij∈E为能找到连通vi和vj的路径(不要求直接连通);S为E的距离属性矩阵，sij∈S为eij的里程;T为E的时间属性矩阵，tij∈T为在eij上行驶的时间;C为E的费用属性矩阵，cij∈C为在eij上行驶的经济成本;P为E的安全属性矩阵，pij∈P为eij的安全概率。配送中心向部队用户配送物资时，每个部队用户的位置和物资需求量已知，要求合理安排车辆和配送路线，以制订配送时间短、配送费用低、配送安全性高的配送方案，并满足以下约束条件:①任何时刻车辆的装载量不超过其最大装载限制;②车辆配送距离不超过其最大行驶距离限制;③部队用户的需求必须满足，且只能由一辆配送车送货，对需求量大于车辆最大载量的部队用户考虑另外单独配送;④车辆必须在规定时间窗内到达部队用户。

2 模型的设计思路

考虑到VRP与推销员回路问题(traveling salesman problem，TSP)的内在联系，本文提出虚设配送中心的思想实现VRP向约束性TSP的转化。

(1)VRP与TSP的相关性概述。TSP是指有一名推销员，从城市1出发，要遍访城市2，3，…，n各一次，最后返回城市1，他应按怎样的次序访问这些城市，才能使总费用最少。而军交运输VRP作为TSP的拓展和延伸，是一个约束性多回路的TSP问题。VRP的多回路特性比TSP具有更复杂的特性，因此，本文提出虚设配送中心的构想，以消除VRP的多回路特性［5］。

(2)虚设配送中心构想的提出。VRP和TSP最本质的差异是前者具有多回路特性，后者只是单环路问题。本文提出的虚设配送中心的构想能够很好地消除这一差异(如图1所示)。具体描述为:在满足给定约束条件的前提下，配送中心出动m辆车向n个部队用户输送物资的VRP是一个节点数为n+1，具有m条回路的约束性TSP。虚设与原配送中心位置重合的m－1个配送中心(原配送中心编号为1;虚拟配送中心编号分别为2，3，…，m;部队用户编号为 m+1，m+2，…，m+n)。规定第1辆车装载一定的物资从1#配送中心出发，完成对若干部队的补给任务后以空车状态回到2#配送中心，第2辆车装载一定物资从2#配送中心出发，对未被补给的若干部队用户进行补给后以空车状态回到3#配送中心，依次类推，第m辆车装载一定物资从m#配送中心出发，对剩下的部队用户进行补给后再回到1#配送中心，这m辆车的m条路径贯穿起来实际上就是一条推销员回路。这样，原本n+1个节点的约束性m条回路的TSP转化成了n+m个城市的约束性单回路TSP问题。规定所有(虚拟)配送中心之间的距离sij为0，安全概率pij为1，其他节点之间的距离sij可以通过Floyd算法求得，进而易求得时间tij和费用cij。

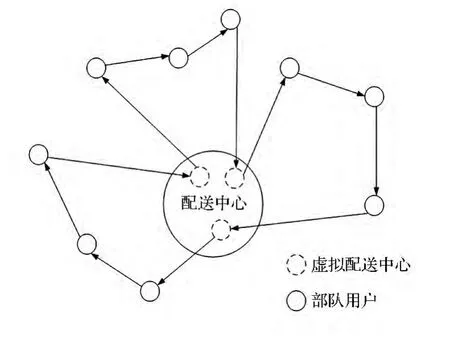
图1 单配送中心VRP虚设配送中心示意

(3)与传统模型的优劣分析。传统VRP模型一般将决策变量设置为三维下标的形式，如用0－1变量xijk表示第k辆车依次对vi和vj进行补给，对于节点规模为20，动用5辆车进行配送的案例，决策变量数为20×20×5。而采用本文的建模思想，只需采用二维下标的决策变量xij即可对问题进行描述，决策变量数为24×24。显然，本文的建模思路将大幅减少决策变量和约束条件数量，大大降低模型复杂度，有效提高求解效率。

3 单配送中心单车型带时间窗装卸一体VRP优化模型

(虚拟)配送中心 vi(i=1，2，…，m)计划派出m辆车(最大载质量为G，最大行驶距离为L)对需求量为gi的n个部队用户 vi(i=m+1，m+2，…，m+n)进行物资配送，同时将需要后送的物品及装备hi带回配送中心，要求制订快速、精确、安全、低成本的配送方案。不同战场环境下，配送任务的优化目标不同，分别以部队用户的平均等待时间TIME、总费用 COST和总安全概率的对数值 ln(SAFETY)为目标函数，建立多目标 VRP优化模型:

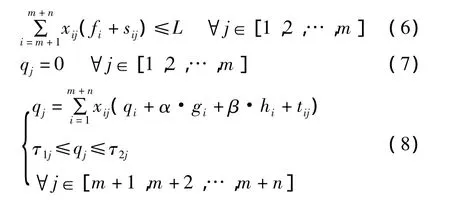
式中:qj为车辆到达vj的时刻;Oj为离开vj时的载质量与出发时相比减少的量;sij为车辆由vi至vj的里程;gj、hj分别为 vj的需求量、后送量;fj为车辆到达vj时行驶的距离;α、β分别为装、卸载速度;τ1j为到达vj的最早时刻;τ2j为到达 vj的最晚时刻;xij为决策变量。

该模型属于0－1非线性规划模型，考虑到对数函数的单调性，取安全概率(SAFETY=∏pijxij)的对数值为优化目标，不影响决策结果。式(1)构成了可行解必须是一条遍历所有节点的回路，且除此不包括其他任意路段的充分必要条件［6］;式(2)、式(3)描述了车辆在运行过程中的装卸货情况及最大载质量约束;式(4)—(6)描述了车辆的运行距离及受到的最大行驶距离约束;式(7)、式(8)描述了车辆到达每个部队用户的时刻及受到的时间窗约束。

4 多配送中心多车型带时间窗装卸一体VRP优化模型

该模型以两个配送中心，两种车型为例说明。假设两个配送中心分别计划派出m辆车和M辆车，对n个部队用户进行物资补给。虚设配送中心后，在1#配送中心的位置共有m+1个(虚拟)配送中心 vi(i=1，2，…，m+1)，在 2#配送中心的位置共有M+1个配送中心vi(i=m+2，m+3，…，m+M+2)，如图2所示。规定任意两个(虚拟)配送中心之间的距离和运输耗时均为0，安全概率为1，其他距离按实际距离计算。

已知1#配送中心和2#配送中心所配备车辆的最大载质量分别为G1和G2，最大行驶距离分别为L1和L2，待补给的n个部队用户vi(i=m+M+3，m+M+4，…，m+M+n+2)的需求量为 gi，后送量为hi，要求制订快速、精确、安全、低成本的配送方案。不同战场环境下，配送任务的优化目标不同，分别以部队用户的平均等待时间TIME、总费用COST和总安全概率的对数值ln(SAFETY)为目标函数，建立多目标VRP优化模型:

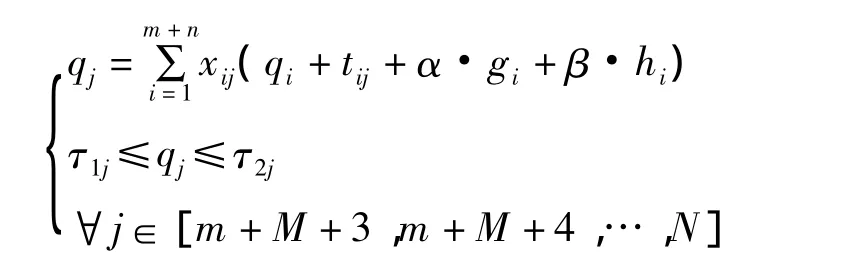
该模型属于0－1非线性规划模型。式(9)构成了可行解必须是一条遍历所有节点的回路，且除此不包括其他任意路段的充分必要条件［6］;式(10)、式(11)对1#配送中心和2#配送中心的车辆的最大载重进行限制;式(12)、式(13)对1#配送中心和2#配送中心车辆的最大行驶距离进行限制;其他变量和约束条件的含义同单配送中心模型。

图2 多配送中心VRP虚设配送中心示意

5 模型求解分析

大规模作战军交运输路径优化问题可以归结为规划问题，其中VRP属于0－1非线性规划问题，多路径多式联运和车辆路径问题属于非线性规划。这些规划问题涉及变量多，约束条件表达式比较复杂，用手工计算求解几乎是不可能的，运用各种元启发式算法编程计算虽然可行，但工作量大、程序长而繁琐，选择参数和终止条件对求解有一定影响，且往往难以求得全局最优解。所以，本文选择专用的求解非线性规划软件——LINGO进行编程求解。

6 想定案例分析

前方配送中心接到战略物流中心补给的物资后，最多可以派出5辆载质量为8 t的车，向8个部队用户进行物资配送，要求5 h内必须全部送达。其中，一对一配送方案优化相对简单(适用于需求量大于车辆载质量的情况)，因此本想定案例中考虑的是一对多的情况。考虑到前方配送中心的给养物资大多情况是由上级调拨来的，可以不考虑其来源和量的限制，因此在这里只考虑物资不受限情况下的一对多配送，这种配送方式在当前配送中心为部队用户配送给养物资的活动中具有代表性［7］。

由于上级调拨的时间限制，以及卸货、装车等原因，汽车只能在早上7:00从前方配送中心出发，受路况影响途中平均速度为50 km/h，车辆最大行驶距离为400 km，平均卸货速度为0.1 t/min，已知配送中心和各部队用户的距离，以及各部队 用户需求量见表1。

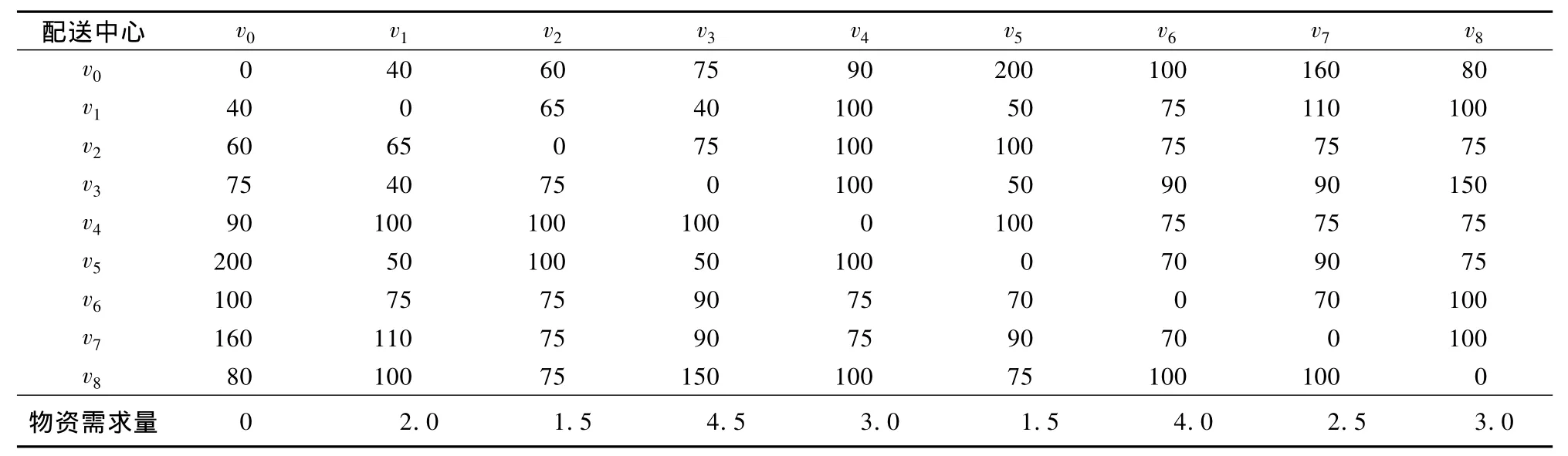
表1 部队用户与配送中心距离及物资需求量

运用单配送中心单车型带时间窗的VRP优化模型，选定优化目标(以平均等待时间最短为例)，通过LINGO软件进行求解仿真，求得全局最优解，制订出两套预案(见表2)。结果表明:出动3辆车能以最短的里程完成任务，车辆最晚到达部队用户(v6)的时刻为11:51，平均等待时间为2.6 h;出动4辆车时总里程增加170 km，最晚到达的部队用户(v7)的时刻为10:48，平均等待时间为2.21 h。对于紧急物资的配送，可选择出动4辆车的方案，一般物资的配送可选择派出3辆车即可。

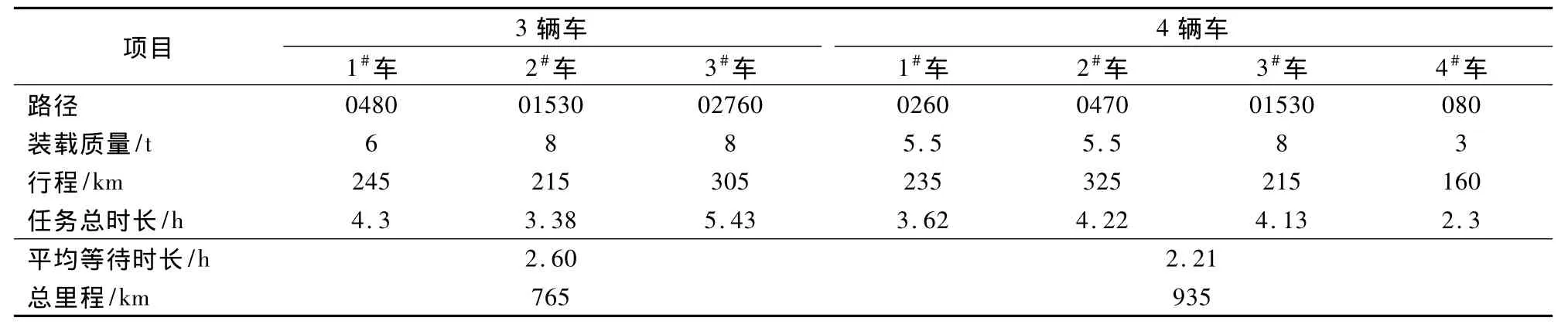
表2 车辆路径问题仿真结果

7 结语

随着全面建设现代后勤的深入推进，军事物流信息化建设加速发展，可视化技术和射频识别技术等物流技术广泛应用，如何更好地运用计算机辅助决策来制订高效的军事物流配送方案，实现资源和运力的优化配置，是从管理学视角提高军交运输保障能力和决策科学化水平的重要途径，对于实现快速保障、精确保障、高效保障意义重大。

［1］ 潘小霞.应急作战军事物流配送方案优化研究［D］.镇江:江苏大学，2010.

［2］ Dantzig G B，Ramser J H.The truck dispatching problem［J］.Management Science，1959，6(1):80-91.

［3］ Rajmohan M，Shahabudeen P.Genetic algorithm based approach for vehicle routing problem with time windows［J］.International Journal of Logistics Systems and Management，2008，4(3):338-365.

［4］ Bazgan C，Hassin R，Monnot M.Approximation algorithms for some vehicle routing problems［J］.Discrete Applied Mathematics，2005，164(1):27-42.

［5］ 张锦，宋业新，李芳，等.基于TSP的军交VRP优化模型及其求解［J］.数学的实践与认识，2011，41(22):162-166.

［6］ 袁新生，卲大宏，郁时炼.LINGO和EXCEL在数学建模中的应用［M］.北京:科学出版社，2006:75-77.

［7］ 周峰.部队给养物资配送方案优化模型及其应用研究［D］.长沙:国防科学技术大学，2008.