二级供应链系统的三阶段协同订货模型

熊 浩，鄢慧丽

（1.海南大学经济与管理学院，海南海口 570228；2.中南大学交通运输工程学院，湖南长沙 410083；3.海南大学旅游学院，海南海口 570228）

二级供应链系统的三阶段协同订货模型

熊 浩1，2，鄢慧丽3

（1.海南大学经济与管理学院，海南海口 570228；2.中南大学交通运输工程学院，湖南长沙 410083；3.海南大学旅游学院，海南海口 570228）

生产商-销售商联合生产库存系统是供应链的一个重要组成部分。但是目前协同条件下的相关订货策略具有明显的局限性，容易丢失真正的最优策略。本文利用边际分析法，通过改变销售商相邻两次订货量的大小来分析生产商和销售商库存费用的变化，发现销售商的订货量与系统库存费用变化量的确存在一定的规律。并且，进一步可以推导出该类系统的最优订货策略的订货量必须符合“三阶段”规律。根据该特点，只需设置各个阶段的初始订货量和订货次数等6个决策变量就可以构建订货策略的数学模型。该模型与直接求解的数学模型相比，不仅变量减少，而且其求解也相对简单。最后，利用各个文献中常用的两个实例仿真进行对比分析，验证了该策略确实能够找出其他策略丢失的最优解。

二级供应链；生产商-销售商；联合系统；三阶段协同订货

1 引言

生产商-销售商联合生产库存（Vendor-Buyer integrated Production-Inventory，VBPI）问题较早由Banerjee［1］于1986年提出，越来越受到关注和重视，并逐渐延伸到多种复杂的情况：一方面是对不确定情况下的库存控制策略研究，如：随机前置期和随机需求［2］；另一方面是对不同的买卖双方合作关系下库存控制策略研究，如：寄售托销关系［3］、有数量折扣条件［4］、商业信用条件［5］、主从关系［6］等。

但是，对于确定需求协同条件下的库存控制策略仍然具有改进空间。Banerjee对于协同策略率先给出了批对批（Lot-for-Lot）的联合经济批量JELS（Joint Economic-lot Size）供货模型。后来，Goyal［7-10］对联合经济批量模型进行了多次改进，提出了供货周期“n次等量订货”的订货策略，接着又提出“按比例P/D多次递增订货量”的订货策略，后来又提出“第一次小批量订货，后面的等批量订货”的订货策略，最后还提出“等比例修正订货量”的订货策略；Hill［11］认为如果VBPI系统按固定比例递增订货量的订货策略，则该比例应该在1到P/D之间。以上这些研究都在试图探寻在VBPI系统中周期内订货量之间的关系，但是在研究这种关系时都假设先生产后供货，而实际上企业运营也存在一边生产一边供货的情况。

因此，Lu Lu［12］对VBPI系统库存问题的前提假设进行了改进，由“先生产后供货”变成了更接近现实的“边生产边供货”。这时VBPI系统的订货策略可能就会更加复杂一些。学者王圣东［13］和周永务［14］都认为这种条件下的VBPI系统中，其最优订货策略中不一定存在订货比例关系，而是需要直接应用数学算法进行求解。本文作者在最近的研究中也给出了更一般化的策略研究［15-16］。

并且，当在一个周期内订货次数增加时，其数学模型中的变量数将会成倍增加。因此，有必要研究VBPI系统中最优订货策略的一些规律，来减少模型的复杂性。本文通过对销售商的边际订货量与系统库存费用变化关系的分析，发现系统销售商订货量与系统库存变化存在一定的机理，并利用该机理推导出系统库存费用变化机理，从而得到了VBPI最优订货策略的“三阶段”规律，然后利用该规律构建“三阶段”订货策略及其数学模型。另外，本文还分析了“三阶段”订货策略与其他策略之间的关系，表明“三阶段”订货策略相比其他策略具有更加广泛的应用范围。最后，利用两个具有代表性的实例对这些订货策略进行了验证，结果证明了“三阶段”策略确实能够找到被其他策略丢失的最优解。

2 问题描述

本文的二级供应链系统是指由生产商和销售商构成的系统。其中，销售商依据其面临的顾客需求向生产商订货；生产商负责产品的生产，并按照销售商的订货进行发货；系统运行时，要求销售商的订货策略在满足顾客需求条件下使整体库存成本最低。该系统一般假定：（1）销售商面临的是确定性需求；（2）系统运行在无限时间水平上且不允许缺货，所以一般假定生产率大于销售率；（3）前置期为零，且不单独考虑运输费用（可以包含在订货费之中）；（4）系统策略具有周期性，且供货商在策略周期只生产一次，即生产商在供货期间可能存在两种状态：生产阶段和停产阶段。

该类问题的基本参数设置如下：P表示生产商的生产率；D销售商的需求率；A1、A2分别表示生产商的生产调整费用、销售商的订货费；h1、h2分别表示生产商的库存费率、销售商的库存费率；qj、qj+1表示销售商相邻两次订货的订货量；Δqj、Δqj+1表示销售商相邻两次订货量的变化量；ΔQb、ΔQv销售商、生产商的库存变化量；HB分别表示销售商平均库存。

3 订货策略对系统库存费用的影响分析

3.1 分析的原理及步骤

在VBPI系统中，对于销售商自身而言，各次的订货量相等时其库存费用最少；而对于生产商来说，此时其库存费用并不是最优。所以，对整个系统而言，有必要分析销售商订货量不相等时销售商和生产商的库存费用变化情况。具体的分析步骤为：

首先，在任意给定的初始策略中，随机抽取相邻的前后2次订货。

然后，在保持这2次订货的订货量之和不变的前提下，对2次订货的订货量进行改变。前后2次订货的订货量之和不变，是为了不改变原订货策略的订货次数。所以，当一次订货增加时，则另一次订货就减少相同的量。

接着，根据这种增加和减少来分析生产商的库存时间量变化情况。

最后，根据销售商的库存时间量和生产商的库存时间量来分析系统的库存费用变化。库存时间量是指库存量与其相应的库存时间的乘积。因此，库存成本可以由库存时间量与库存费率的乘积表示。

需要注意，销售商相邻两次订货的订货时间，可能都处于生产商的生产阶段或停产阶段，也有可能前次订货处于生产阶段而后次订货处于停产阶段。这两种情况下生产商的库存时间量随订货量的变化所发生的变化不一样，下面将分别对其进行分析。

3.2 相邻2次订货同时发生在生产阶段或停产阶段

首先，从原始订货策略中选中销售商的2次订货为第j和j+1次订货，其订货量分别为的关系为qj和qj+1。为了分析的方便，假设qj＜qj+1。然后，对这2次订货的订货量进行调整：前次订货增加量Δqj，后次订货量减少Δqj。则此时销售商的库存时间量（库存量乘以时间）的增加值为（如图1所示，点纹阴影面积减去横纹阴影面积）：

若销售商的这2次订货发生的时间都在生产商的生产期间或停产期间时，生产商的库存时间量的减少值为（如图2、图3所示，点纹阴影面积减去横纹阴影面积）：

由式（1）和式（2）可得ΔQv=ΔQb，说明销售商的库存变化与生产商的变化方向相反，且数量相等。这表明，在生产商的生产期间或停产期间，订货策略的改变对系统总的库存时间量没有影响。但是，如果生产商和销售商的单位库存费用不同，则订货策略应该使库存更多的存放到单位库存费用较少的一方。比如：如果生产商处的单位库存费更低，则销售商尽可能采用等量订货，这时产品库存将更多的偏向生产商一方，虽然整体库存不变，但是库存费用降低了。

3.3 相邻2次订货的前次在生产阶段后次在停产阶段

对于VBPI系统，其订货策略可能出现这样一个种情况：销售商的前次订货发生在生产商的生产阶段而后次订货发生在生产商的停产阶段（如图4）。在这种情况下，生产商的库存时间量增加值ΔQ+和库存时间量减少值ΔQ-分别如图4中的点阴影区和横线阴影区所示，可以推导出：ΔQ+＞（qj+1-。则生产商库存时间量的减少值为：

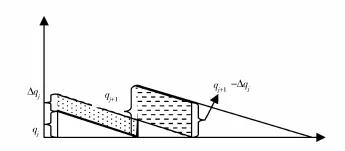
图1 销售商的库存变化

图2 生产期间生产商的库存变化

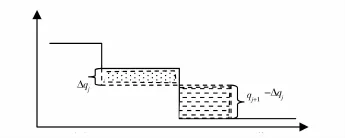
图3 停产期间生产商的库存变化

图4 交界期间生产商的库存变化

式（3）结合式（1）可推导出不等式：ΔQv＞ΔQb，即生产商的库存时间量减少值大于销售商的库存时间量增加值。由此可知，当销售商采用非等量订货策略时，销售商库存时间量会增加，而生产商的库存时间量会减少，且减少量比增加量大，所以系统的库存时间量也会减少；反之，当销售商等量订货时，系统的库存时间量会增大。但是，需要注意，虽然库存时间量变化情况弄清楚了，但库存费用的变化还与生产商和销售商的库存费率有关。

4 “三阶段”订货策略

4.1 “三阶段”订货策略的推导

为了分析的方便，假设生产商单位库存费率低于销售商单位库存费率。随机给定一个销售商订货量递增的初始订货策略，然后对该策略进行调整来减少库存成本。调整的方法就是根据第2节的分析，尽可能的缩小前后两次订货量差距，使销售商库存减少、生产商的库存增加，从而减少总体库存成本。调整后的策略不仅降低了库存成本，而且呈现出具有三个不同阶段的订货量规律。

（1）生产阶段。对于初始策略中，在生产商生产阶段选取销售商的第j次和j+1次订货。Ij是生产商在订货点j的库存剩余量，不能为负。所以Ij是可以对销售商第j次订货量的最大增加量，即Δqj≤Ij。

①当两次订货量的差距大于2Ij，即：（qj+1-qj）＞Ij。为了缩小第j次和第j+1次的订货量差距，第j次订货的订货量能够增加的最大量为Ij，第j+1次减少同样的量。此时，第j次仍然小于或等于第j+1次订货量，即：

②当两次订货量的差距小于2Ij，即：（qj+1-qj）＞Ij。此时，通过调整可以使前后的两次订货量达到相等，从而使库存发生最大偏移（销售商库存降最低，生产商库存增加）。

（2）停产阶段。如果第j次订货时，生产商已经停止生产，此时第j次订货后的库存剩余量能用来满足所有后面的订货，所以一定有：Ij≥qj+1＞qj+1-qj≥2Δqj，满足（qj+1-qj）≤Ij，则前次的订货量最多能增加（qj+1-qj），此时是本次和其相邻的下次订货量相等。

由以上分析可知，由于在生产商处于生产阶段的时候库存量较少，此时若要减少两次订货的差距只有使前几次订货的订货量尽可能的大，即前几次订货后的生产商剩余库存为零；而这之后就可能等量订货了。所以，订货量随着生产的进行会不断增加，增加到一定程度之后不能再增加，进行等量订货。等量订货的过程中生产商的剩余库存会增加（因为生产率大于需求率），这时候可以实现较长时间的等量订货；但是由于生产时间的因素使得订货策略可能存在交界阶段，交界阶段的前后两次订货的订货量大小对库存偏移（使更多的库存存放到生产商处）具有不确定性，所以销售商在生产商生产阶段的订货量与在生产商停产之后的订货量不一定相等。

综上所述，供货周期开始时的生产商的初始库存q0量给定时，可以将生产商-销售商联合库存模型的订货策略分成三个不同的阶段构成：（1）第一个阶段：使生产商库存为零的递增订货，可以计算出这时的递增比例为生产率和需求率之比P/D；（2）第二阶段：按照相等的订货量订货。（3）第三阶段：停产之后的订货，采用相等的订货策略。

4.2 “三阶段”订货策略的数学模型

依据前面的“三阶段”订货策略，进一步构建数学模型来确定具体的订货方案。构建数学模型需要的参数设置如下：k1、k2分别表示生产阶段按P/D增量订货的订货次数、生产阶段等量订货的订货次数；k3表示停产阶段等量订货的订货次数；q0表示周期开始时生产商的初始库存；q3表示第3阶段（停产期内的等量订货阶段）的单次订货量；λ1表示第一阶段增量订货的递增比例，λ=P/D；λ2表示第二阶段的各次订货的订货量与第一阶段的最后一次订货的订货量比例；Q表示销售商在整个供货周期的订货量之和。

综合上节的论述，可以将VBPI系统订货策略的数学模型［10］简化为仅包含6个变量。简化的数学模型如下：

其中：

上述公式中，式（4）表示系统订货相关的总平均费用；式（5）表示销售商在供货周期内的订货量；式（6）表示销售商的平均库存量；式（7）表示了第三阶段订货与其前面的各次订货之间的关系：供货周期的长度不小于前两个阶段订货时间之和；停产之后的订货量总和应该小于第二阶段结束时生产商库存量的最大值；式（8）是基本的约束条件。

可见，无论订货次数是多少，“三阶段”订货数学模型只需要6个变量，从而降低了求解的难度，更容易获得最优解。

5 策略的对比分析及实例演算

5.1 策略的对比分析

“三阶段”策略与目前已有文献中的相关策略相比较，“三阶段”策略适用范围更广，更具有一般性（见表1）。

（1）当k1≠0，k2=0，k3=0时，只有第一阶段时的订货策略就是Goyal的P/D比例递增订货策略；

（2）当k1=0，k2≠0，k3≠0时，没有第一阶段订货，如果第二段和第三阶段的订货批量如果刚好相等，则构成了Lu的等量订货策略；

（3）当k1=0，k2=0，k3≠0时，没有第一阶段和第二阶段时，就出现了Lu关于VBPI模型的分类的第一种，即先生产再供货。

表1 “三阶段”策略和其他策略之间的关系

5.2 实例计算验证

例1：我们考虑Goyal［8］的例子1：A1=400，A2=25，h1=4，h2=5，P=3200，D=1000。本文利用“三阶段”订货策略进行求解，得到的最优解为：q0=7.39、k1=2、k2=1、k3=1、q3=228、λ2=3，因此，周期开始时的原始库存为7.39，然后按λ1= P/D=3.2的比例递增订货2次（第一阶段订货量：24、76），然后按照等量λ2qk1=3×76=228订货1次（第二阶段订货量：229），最后按照229订货1次（第三阶段订货：229），总成本为1792。

与其它模型得到的订货策略的系统平均成本相比，本文的订货策略的平均成本最低（见表2）。

表2 例1中不同策略的结果比较

表3 例2中不同策略的结果比较

例2：我们考虑Goyal［8］的例子2：A1=400，A2=25，h1=4，h2=7，P=3200，D=1000。本文利用“三阶段”订货策略进行求解，得到的最优解为：q0=9.72、k1=2、k2=1、k3=2、q3=134、λ2= 1.38，因此，周期开始时的原始库存为9.72，然后按λ1=P/D=3.2的比例递增订货2次（第一阶段订货量：31、99），然后按照等量λ2qk1=1.38×99= 137订货1次（第二阶段订货量：137），最后按照13订货2次（第三阶段订货：137、137），总成本为193。

与其它模型得到的订货策略的系统平均成本相比，本文的订货策略的平均成本最低（见表3）。

以上两个实例中，“三阶段”订货模型不仅使求解变得相对容易，而且能得到了使成本更低的订货策略，说明VBPI系统中的“三阶段”订货策略确实具有较好的效果。

6 结语

本文通过对销售商订货量与系统库存时间量的变化关系进行分析，利用订货量与库存费用变化的机理，推导出了生产商-销售商联合生产库存管理最优订货策略的“三阶段”规律，并依据该规律简化了VBPI系统的订货策略数学模型。与其他策略的相比，“三阶段”策略不仅相对简单，而且适用范围更广。最后，通过实例计算的对比分析，验证了该策略的优化效果。

［1］Banerjee A.A joint economic-lot-size model for purchaser and vendor［J］.Decision sciences，1986，17（3）：292-311.

［2］Glock C H.Lead time reduction strategies in a singlevendor-single-buyer integrated inventory model with lot size-dependent lead times and stochastic demand［J］.International Journal of Production Economics，2012，136（1）：37-44.

［3］Hariga M，Gumus M，Ben-Daya M，et al.Scheduling and lot sizing models for the single-vendor multi-buyer problem under consignment stock partnership［J］.Journal of the Operational Research Society，2012，64（7）：995-1009.

［4］Giri B C，Roy B.A vendor-buyer integrated productioninventory model with quantity discount and unequal sized shipments［J］.International Journal of Operational Research，2013，16（1）：1-13.

［5］Teng J，Chang C，Chern M.Vendor-buyer inventory models with trade credit financing under both non-cooperative and integrated environments［J］.International Journal of Systems Science，2012，43（11）：2050-2061.

［6］Giri B C，Bhattacharjee R.An optimal policy for a single-vendor single-buyer integrated inventory system based on vendor's strategy of shipments to buyer［J］.International Journal of Services and Operations Management，2012，13（2）：267-278.

［7］Goyal S K.A joint economic-lot-size model for purchaser and vendor：A comment［J］.Decision Sciences，1988，19（1）：236-241.

［8］Goyal S K.A one-vendor multi-buyer integrated inventory model：A comment［J］.European Journal of Operational Research，1995，82（1）：209-210.

［9］Goyal S K，Nebebe F.Determination of economic production-shipment policy for a single-vendor-single-buyer system［J］.European Journal of Operational Research，2000，121（1）：175-178.

［10］Goyal S K.On improving the single-vendor single-buyer integrated production inventory model with a generalized policy［J］.European Journal of Operational Research，2000，125（2）：429-430.

［11］Hill R M.The single-vendor single-buyer integrated production-inventory model with a generalized policy［J］.European Journal of Operational Research，1997，97：493-499.

［12］Lu Lu.A one-vendor multi-buyer integrated inventory model［J］.European Journal of Operational Research，1995，81（2）：312-323.

［13］王圣东，单供货商多销售商联合生产库存模型［J］.系统工程学报，2006，21：92-95.

［14］Zhou Yongwu.Optimal production and shipment models for a single-vendor-single-buyer integrated system［J］.European Journal of Operational Research，2007，180（1）：309-328.

［15］熊浩，孙有望.生产商-销售商联合生产库存问题的一般数学模型［J］.同济大学学报（自然科学版），2012，（2）：315-319.

［16］熊浩.单生产商-多销售商多生产阶段协同订货模型［J］.上海交通大学学报，2011，（12）：1760-1764.

A Three-Phase Synchronized Shipment Model of Two-Echelon Supply Chain System

XIONG Hao1，2，YAN Hui-li3
（1.School of Economics and Management，Hainan University，Haikou 570228，China；2.School of Traffic and Transportation Engineering，Central South University，Changsha 410083，China；3.Tounism College，Hainan University，Haikou 570228，China）

The vendor-buyer integrated production-inventory system is an important component of the supply chain operation.So far，more and more literatures have been interested on this theme.However，all the shipment policies hitherto been presented have obviously defects which will lose the optimal order scheme.In this paper，the marginal analysis method is used to analyzed the relationship between the change of order quantity and system inventory cost.Firstly，the buyer's quantities of the twice adjacent orders are adjusted while keeping their whole quantity unchanged.Then，both the producer's and the buyer's inventory and their inventory cost are recalculated.Finally，a＂three phase＂rule of the best order strategy of this system can be deduced.First stage is the increase ordering stage during the first part of the producer's production.And the buyer needs to increase the ordering quantity according to the ratio of the productivity and the demand rate.The second stage is the equal ordering stage during the second part of the producer's production.And the buyer will make several ordering with certain equal ordering quantity in this stage.The third stage is the equal ordering stage after the vendor's production，which means the buyer will make several ordering with equal ordering quantity after production.According to this characteristic，the corresponding mathematical model of ordering strategy can be constructed by only six variables，which include the quantity and the times of ordering during the various stages.Compared with the other direct mathematical model with every possible number of the order and their ordering quantities，not only the variables of the model are reduced，but also the solution process is become relatively simple.Finally，two simulation examples commonly used in many literatures are analyzed.And the result shows that this strategy can actually find the optimal solution while other strategies lost.

two-echelon supply chain；vendor-buyer；integrated system；three-phase synchronized shipment

N945；F406

：A

1003-207（2014）05-0069-06

2012-04-16；

2013-09-02

国家自然科学基金资助项目（71271220，71061005）；中南大学博士后基金资助项目（126227）；中西部高校综合能力提升计划项目资助

熊浩（1981-），男（汉族），湖北石首人，海南大学经济与管理学院，讲师，中南大学交通运输工程学院博士后，研究方向：物流工程、交通运输规划与管理.