基于NSGA-II的维修器材仓库多目标货位分配规划

于战果，邓 威，张 尧，杨冰峰

(1.军事交通学院后勤装备勤务保障中心，天津300161;2.军事交通学院 研究生管理大队，天津300161)

存储是仓库的一项主要功能，缩短出入库的 搬运距离，提高作业效率，提升器材保管水平的关键就在于科学合理的货位管理，也就是将各种器材依据一定的原则安排在货架的指定位置，以实现器材搬运的低成本、高效率［1－2］。

1 多目标货位分配模型

1.1 问题描述

在一个包含a排b列c层的货架存储区，存储区货架布置如图1所示，共有n个货位，需要存储m种器材，每种器材需要Ni个货位，其中

图1 货架区简单立体示意

现在需要按照一定的原则将这m种器材合理地存放到货架上。最靠近出口的排为第一排，最靠近出口的列为第一列，最低层为第一层。位于i排 j列 k 层的货位坐标为(xijk，yijk，zijk)，坐标(0，0，0)为该存储区的出口，记为I/O口，货位的长、宽、高分别为货位沿X、Y、Z轴的长度。根据问题的实际进行如下限定:存储区只有一个出入口，每个货格只存放一种器材，器材的尺寸能够放入货位。

1.2 目标分析

根据维修器材的管理要求和仓库的实际情况，针对器材存储规划时能够进行量化分析的原则，在进行存储货位分配规划时主要考虑以下3个目标。

(1)目标一:搬运距离最短。就是器材存储到货架上后，在分拣搬运出库时减少作业人员行走的总路程。解决此目标的基本思想是将出库数量大且出库次数多的器材放在离出入口较近的货位上。定义Ki为顺序编号为i的器材的年平均出库量，则Ki越高i器材所存货位离出入库距离越小。定义Fi为顺序编号为i的器材的年平均出库频次，即指i器材一年的平均出库次数，Fi越高i器材所存货位离出入库距离也应该越小。

若要使总的搬运距离最小，得到目标函数:

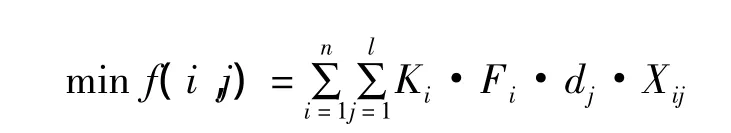
式中:n为需要存放在货架上的器材种类数，若一种器材需要多个货位，则看成是多种器材;l为货架区货位数量，一般有n≤l，即保证每种器材都有位置进行存放;dj为编号为j的货位到出入口的距离;Xij=0或1，Xij=1为i种器材存放在编号为j的货位上，反之Xij=0。

(2)目标二:货架总质心最低。若将较重器材放在货架的上层，而相对较轻的器材放在货架的下层，上重下轻的结构会导致货架发生倾覆的可能性，而且在人工拣选系统中，较重器材存放位置较高也不便于从货架上取出，因此降低货架总质心，器材存放上轻下重也是必须考虑的目标。假设有 n 种器材，质量分别为 m1，m2，…，mn，且分别位于h1，h2，…，hn高度，则此n种器材的总质心 h可以使用如下公式计算:

货位 j的位置坐标为(xj，yj，zj)，则货架的总质心为

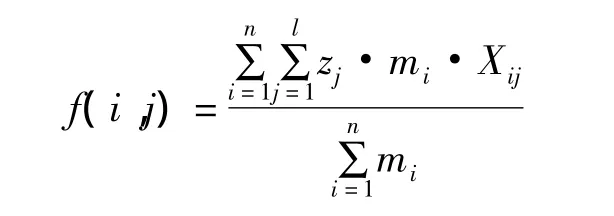
式中:mi为第i种器材的质量，若同种器材只需要一个货位，则为器材的入库质量，若需求多个货位，则为该种器材单个货位最大存储质量。由于这里的目标是提高货架的稳定性，器材存放上轻下重，因此只需考虑竖直方向上的中心坐标最小，水平方向上无需考虑。

(3)目标三:同种装备维修器材距离近。同一装备的多种周转维修器材经常会同时出库，存储于相邻货位能够方便拣选。假设某一专业共有k种装备，第i种装备共有Ni种周转维修器材，每种维修器材货位的空间位置坐标为(x，y，z)，则Ni种维修器材的位置组合向量为

定义rj为第j种器材和该类器材中心的偏离距离，则

1.3 模型建立

针对以上货位分配规划的3个目标，建立如下多目标数学规划模型:

式中Rg为第g种装备维修器材的总偏离距离。

以上通过建立一个多目标数学规划模型对货位分配规划的优劣性进行数学描述，此数学模型能够有效地反映出货位分配的3个指标要求，实现从“现实问题”向“抽象数学空间”的转变。

2 算法设计

本文建立的是一个多目标规划问题，求解多目标问题主要有两种基本思路:一是先决策再优化，最为代表的是权重系数法;二是先优化再决策，常用的是多目标进化算法。由于先决策的方法需要掌握问题的先验信息，而通常获得这些信息是比较困难的，这里采用先优化再决策的方法。算法分为两个阶段:第一阶段通过NSGA－II进化算法得到多目标问题的Pareto解集，即得到多个货位分配方案;第二阶段运用Topsis方法对多个方案进行优选。

2.1 NSGA-II进化算法

目前多目标进化算法有很多，Kalyanmoy Deb的带精英策略的快速非支配排序遗传算法［3］(nondominated sorting genetic algorithm II，NSGAII)是应用最广泛、求解效果最好的一种。NSGA-II是一种求解多目标问题的遗传算法，由Deb等人在2002年在对NSGA算法改进的基础上提出。NSGA-II算法采用个体的非支配层次作为适应度，适应度是通过快速非支配排序得到的。在维护种群的多样性方面，NSGA-II首次引入了拥挤距离的方法，还使用了(μ+λ)的精英保留策略。NSGA-II中两个最重要的函数是快速非支配排序函数和拥挤距离计算函数，具体计算方法可参见文献［4］。

2.2 基于Topsis的方案优选

Topsis法是 C.L.Hwang和 K.Yoon于1981 年提出，是依据各方案到理想解的距离进行排序选优的方法，适用于解决多属性决策问题。在本文中，多目标进化算法求得的非劣解集作为待决策方案，3个目标作为各方案的属性，目标值是各属性的取值，属性权值是决策者的偏好信息，因此运用Topsis方法是可行的。具体计算方法可参见文献［5］。

3 算例分析

3.1 基础数据

应用上述建立的模型和求解方法对某装备维修器材仓库仓储区初始货位分配进行规划。每排货架为10列5层，单个货格的长宽高均为一个单位，巷道宽度为两个单位。这里以两排货架共100个货位入库100种器材为例进行规划。各种器材的基础信息见表1。

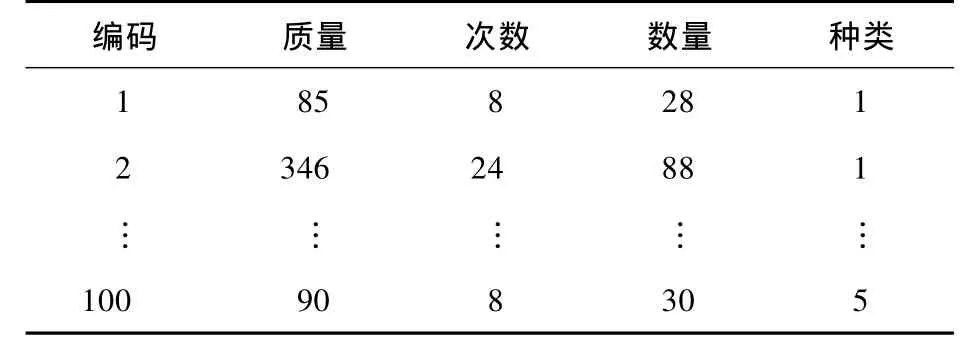
表1 器材基础信息

为便于使用遗传算法求解，对货位采用如下方式的顺序编码，以b列c层为例，若有多排，顺序号依次顺延(如图2所示)。

3.2 求解结果

编码是建立问题空间和模型空间联系的枢纽，针对问题特点，本文采用符号编码方式。器材编码顺序不变，通过变换货位编码的不同顺序，可以得到不同的染色体(编码示例见表2，遗传算法控制参数见表3)。

图2 顺序编码示意

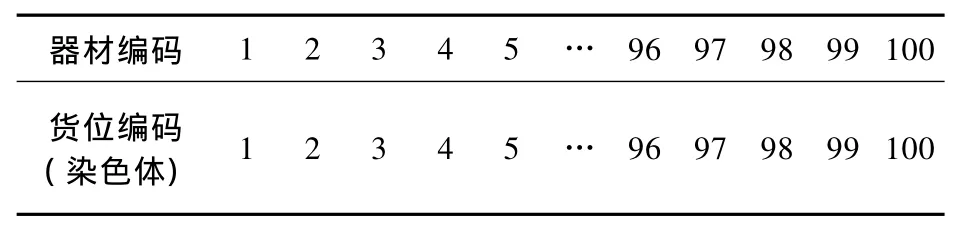
表2 编码示例

表3 遗传算法控制参数

通过在Matlab 7.5平台上编写程序实现上述算法。其中选择、交叉、变异等遗传操作同基本遗传算法，具体可参见文献［6］。结果如图3—6所示。

图3 第一目标函数性能迭代

通过3个目标函数的性能迭代图可以发现，随着迭代次数的增加，3个目标值均出现了明显的下降，到1 000代之后逐渐趋于稳定，相对于初始随机生成的货位分配方案，最终方案的目标值显然较好，说明本文方法具有较好的优化效果。

通过上文的计算，得到的Pareto最优解集以Excel的形式输出。由于问题的规模较大，得到的最优解集中解的数量较多，考虑到本文3个目标中更倾向于使第一目标达到最优，通过对第一目标函数值进行升序排列，从中选取前30个，每个解都对应一种货位分配方案(见表4)。

图4 第二目标函数性能迭代

图5 第三目标函数性能迭代

根据2.2节中的Topsis方法，把求解到的30个解作为决策方案，把3个目标作为方案的属性，属性权值为［0.5，0.3，0.2］，通过编程分析，得到最佳协调解为序号20。

通过表5对比可以看出，在多目标模型作用下，最优结果中3个目标函数值相对于初始货位分配方案均明显降低，证明了本文求解方法的可行性。

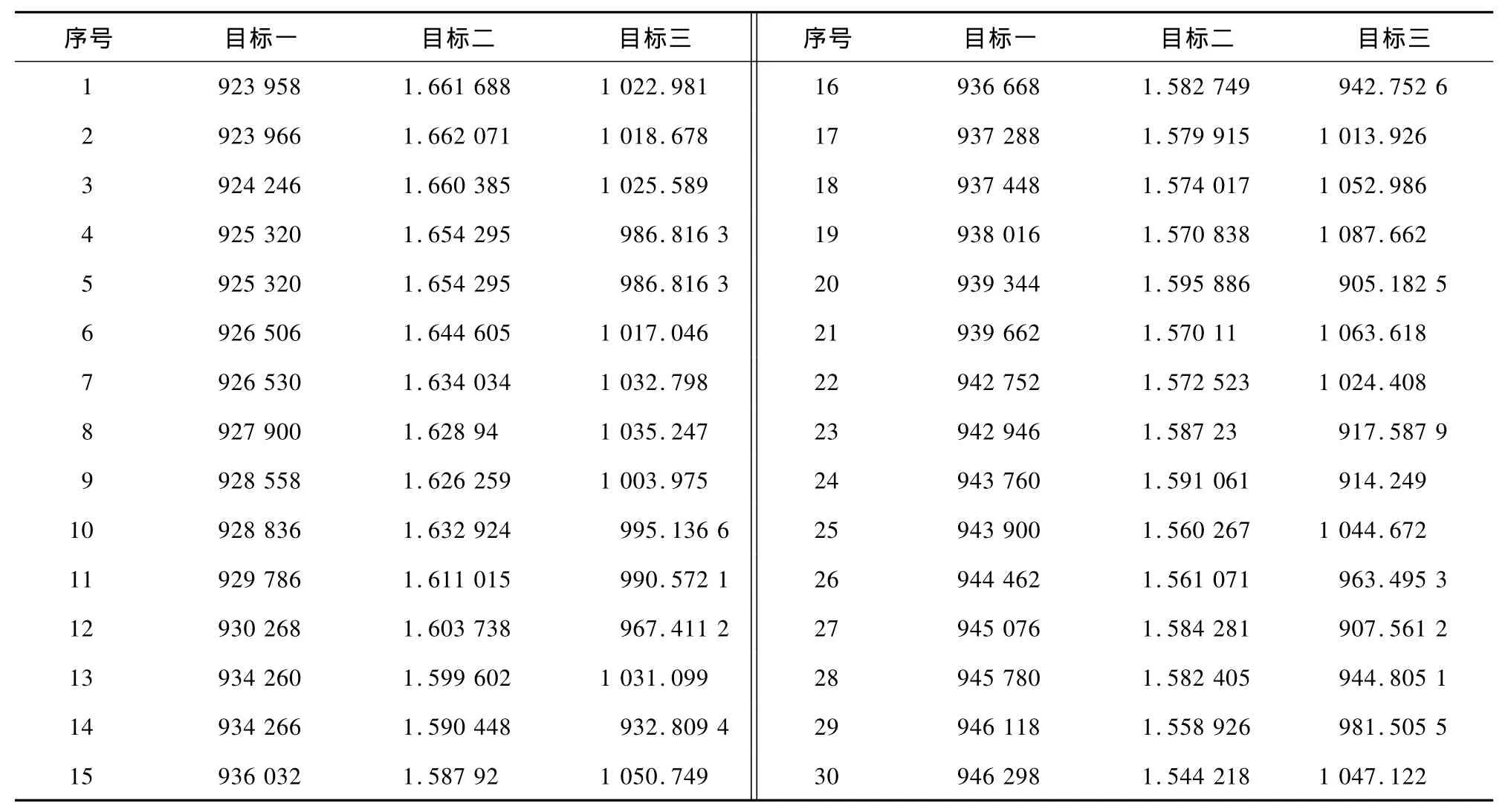
表4 最优方案目标函数值

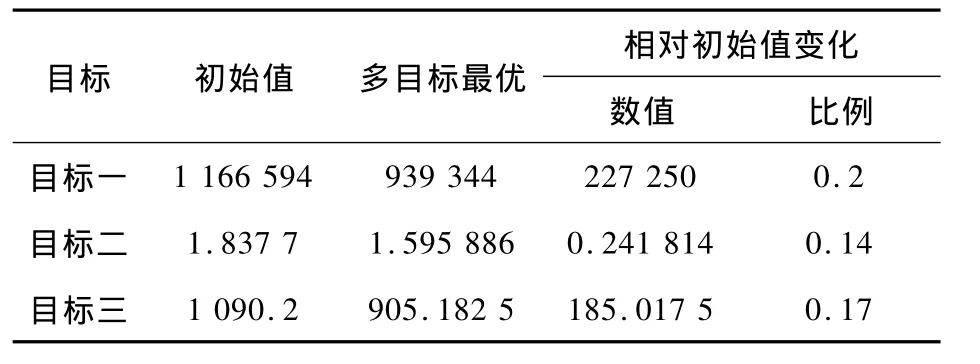
表5 目标函数值对比

对货位分配最优结果对应染色体进行解码，得到货位分配方案如图7、图8所示。

图7 第一排货架器材位置分布

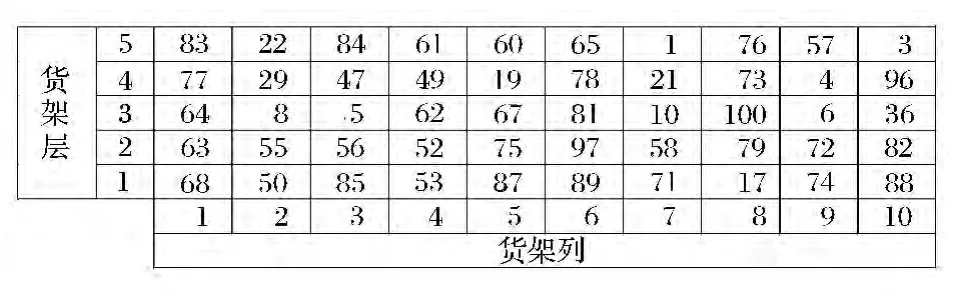
图8 第二排货架器材位置分布

4 结语

本文通过对某器材仓库货位管理中的多个要求进行量化分析，建立了货位分配的多目标规划模型。运用NSGA-II算法得到多目标问题的Pareto解集，即多个货位分配方案，可供决策者选择。根据决策者偏好信息应用Topsis方法得到带附加条件的最优解。经验证本方法能够较好的解决多目标货位分配问题。本文中遗传算法的控制参数是依据经验设定的，可能产生早熟情况，并不能保证收敛于最优Pareto前端。通过设置不同的参数进行求解结果的对比来确定最佳的参数将是下一步研究的方向。

［1］ 郑凌莺.医药物流中心仓库货位优化系统的研究［D］.上海:上海交通大学，2005.

［2］ 程书强.论配送中心的储位规划管理［J］.中国储运，2003(3):50-53.

［3］ Deb K，Pratap A，Agawal S，et al.A fast and elitist multiobjective genetic algorithm NSGA － II［J］.IEEE Transaction on Evolutionary Computation，2002，6(2):182-197.

［4］ 高媛.非支配排序遗传算法(NSGA)的研究与应用［D］.杭州:浙江大学，2006.

［5］ 石黎明，张雄，李少华.基于熵权的TOPSIS法在舰载飞机抢修决策中的运用［J］.系统仿真技术，2013，9(4):350-354.

［6］ 雷英杰.MATLAB遗传算法工具箱及其应用［M］.西安:西安电子科技大学出版社，2005:62-94.