培养学生有序观察能力 促进数学高层次思维发展

刘杰

【摘要】本文所指的有序观察能力就是在数学学习过程中，学生根据观察对象的特点，遵循现实生活或问题情境中的时空、性质及特征之序等进行有效观察，捕捉并提取进行思维的数学信息，触发思维认识规律，形成数学问题解决的能力。为培养学生有序观察能力，促进数学高层次思维发展，笔者在教学实际中采取以下措施开展实践与研究：注重时间与空间顺序，积累有序观察的活动经验；运用细致流畅的语言描述，促进和提高有序观察能力；遵循几何直观规律，有序观察培养空间观念；把握整体与部分关系，有序观察激发创新思维。

【关键词】时空顺序 有序观察 几何直观 创新思维

【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2015）01-0114-02

一、注重时间与空间顺序，积累有序观察的活动经验

一年级学生的数学学习，由于学生的年龄特点，有序观察缺乏活动经验，动作协调能力也很弱，要求他们在杂乱的信息中准确收集数学信息有一定难度，但同时小学生具有较强的模仿学习能力，这对培养有序观察能力也是优势。低段学生学习以形象直观为主，对观察的要求不高，应主要立足于生生、师生间互动交流，借助示范的作用，在改进与模仿中培养按时空、方位顺序，即按照从上到下或从左到右的等空间顺序和事情发生与发展的先后顺序及条理性进行有序观察。

如在一年级下册的减法（一）中，教材目的是初步发展学生从具体情境中通过观察提取数学信息、提出数学问题并进行解答的能力。在教学中，先请学生独立有序观察，老师引导说明：有序观察就是按照从上到下或从左到右的顺序，数出每种动物的只数，然后独立尝试问题解决。在随后的学习反馈中，笔者发现发生计数错误的学生占10—20%，为了了解学生的错误原因，有意识地请发生计数错误的学生在多媒体屏幕或黑板上进行操作再演，全班学生从中观察到该生在从上到下或从左到右数数操作上的问题与不足，吸取经验教训。接着又请数数正确的学生作有序的观察与操作展示，最后老师作进一步的标准示范。这样通过层次分明的互动交流，在演示与模仿中强化了有序观察的方法指导，促进了学生有序观察能力的发展。

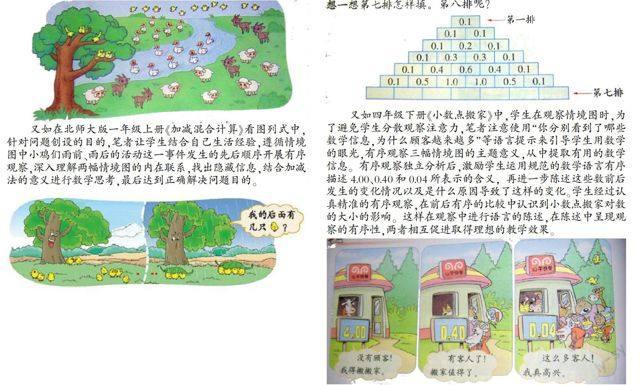
又如在北师大版一年级上册《加减混合计算》看图列式中，针对问题创设的目的，笔者让学生结合自己生活经验，遵循情境图中小鸡们雨前、雨后的活动这一事件发生的先后顺序开展有序观察，深入理解两幅情境图的内在联系，找出隐藏信息，结合加减法的意义进行数学思考，最后达到正确解决问题目的。

二、运用细致流畅的语言描述，促进和提高有序观察能力

言为心声，语言是心灵的再现。观察是主观的知觉行为，要了解学生是否进行有序、有效的观察，是否收集到有用的数学信息，是否有利于进行数学思考，需要学生用语言、文字、符号或式子来描述再现观察的过程与结果，便于教者进行有序观察效果的诊断与矫正，以有利于有序观察能力的形成。

教学实际中，给予学生充分的时间与空间进行有序观察和独立思考，在尝试完成之后，创设宽松的交流汇报环境，让多名学生从不同方法、不同侧面进行思考陈述。通过语言描述，让听众明白了他的观察的顺序：有的看出了左右两端都是0.1，有的看出了每一横排的对称性，有的看出了中间上下两排的加减关系。通过学生清晰而富有逻辑的讲述，学生的不同的观察顺序与思考方式得到充分的呈现，创新的火花得以迸发，数学高层次思维得以展现。

又如四年级下册《小数点搬家》中，学生在观察情境图时，为了避免学生分散观察注意力，笔者注意使用“你分别看到了哪些数学信息，为什么顾客越来越多”等语言提示来引导学生用数学的眼光，有序观察三幅情境图的主题意义，从中提取有用的数学信息。有序观察独立分析后，激励学生运用规范的数学语言有序描述4.00、0.40和0.04所表示的含义，再进一步陈述这些数前后发生的变化情况以及是什么原因导致了这样的变化。学生经过认真精准的有序观察，在前后有序的比较中认识到小数点搬家对数的大小的影响。这样在观察中进行语言的陈述，在陈述中呈现观察的有序性，两者相互促进取得理想的教学效果。

三、遵循几何直观规律，有序观察培养空间观念

遵循空间观念形成规律，对图形形体特征的充分感知是学生开展图形与几何学习的重要手段，而有序观察就是感知的主要手段之一。

在图形与几何学习中，根据几何直观形成规律，首先应直观观察具体的实物，通过物体的直观观察来帮助学生形成对有关物体形状特征的整体认识；其次是观察物体经过抽象呈现的几何视图，通过视图的观察来帮助学生形成对有关物体性质特征的认识；最后通过观察物体及模型的操作及演示，分析有关物体的多种组成要素之间的联系帮助学生构建对物体本质属性的理解与运用。

四、把握整体与部分关系 有序观察激发创新思维

（一）运用部分—整体—部分的观察顺序，发展创新能力

有序观察可以根据部分与整体之间的联系，通过对局部特征分析，找准关键联想点，以小见大，触类旁通，通过积极想象，探究对象本质或对象间的性质关系，促进创新思维的发展。

如圆锥体积学习中，学生最困难的是怎样才能将圆锥有意识的与已学的圆柱间产生联想。教材呈现直白、简单，留给学生猜想的空间比较狭窄，学生创新的思维没能得到有效的锻炼。笔者认为：学生感知圆锥实物特征和底与高后，让学生猜想根据圆锥的特征要做出一个圆锥你会怎样做？（有些同学可能根据已有的经验想到用圆柱来削成一个圆锥）。再进一步引导学生大胆猜测：圆锥的体积与自己的什么有关？它的體积可能与谁的体积关系更为密切？说说你的理由。经过层层推理与猜想，再经历圆锥与等底、等高圆柱的装沙实验后，验证得到圆锥与圆柱体积之间的关系，从而完成了圆锥（部分）—圆柱（整体）—圆锥（部分）的有序观察和慎密思考的探索过程。

（二）运用整体—部分—整体的观察顺序，培养探究策略

心理学认为：人的知觉有一种趋向稳定性、完整性和对称性的倾向，这就是观察的主观性。观察的主观性有时会干扰我们观察的真实与正确性，要保证观察的客观性，就需要掌握一定的观察方法保持观察的本真。在实际的观察中我们根据观察对象的具体情况可以采取整体——部分——整体的顺序，即先观察了解对象整体概况，经过化整为零，从小处着手，借助操作探究，观察分析对象性质，最后回归整体概括得到规律，有如我们常用的化归和列举问题解决策略。

参考文献：

[1]义务教育数学课程标准（2011年版）解读 北师大出版社

[2]《小学数学课程与教学》 主编：杨庆余 中国人民大学出版社