摆线齿准双曲面齿轮齿面主动设计*

杜进辅，方宗德，张永振，李建华

(1. 西北工业大学 机电学院， 陕西 西安　710072; 2. 西安理工大学 机仪学院， 陕西 西安　710048)



摆线齿准双曲面齿轮齿面主动设计*

杜进辅1，2，方宗德1，张永振1，李建华1

(1. 西北工业大学 机电学院， 陕西 西安710072; 2. 西安理工大学 机仪学院， 陕西 西安710048)

摘要：为预控双面法加工的摆线齿准双曲面齿轮的啮合性能，用大轮理论齿面展成与之共轭的小轮共轭齿面，将小轮共轭齿面沿啮合线方向和接触迹线方向分别进行修形，得到满足预置传动误差曲线以及接触印痕的目标齿面，计算出目标齿面与小轮理论齿面的法向偏差。建立以小轮加工参数调整量为变量，小轮两侧齿面与目标齿面法向偏差平方和最小为目标的优化模型，并采用序列二次规划算法求解该模型。以某高速车桥齿轮副为例进行验证，结果表明：加工参数调整后小轮两侧齿面与各自目标齿面的最大法向偏差分别为-4.7μm和-4.67μm，两侧啮合转换点传动误差与预置值分别相差6.67%和4%，两侧接触迹线最大偏差分别为0.275mm和0.177mm，基本符合预置条件。

关键词：双面法；摆线齿；主动设计；修形；序列二次规划算法

采用端面滚齿法加工的摆线齿准双曲面齿轮具有承载能力高、传动平稳、噪声小以及生产效率高、所需设备少等一系列优点，近年来，在轿车、卡车以及客车车桥齿轮中应用越来越广泛，因此研究并改善这类齿轮的啮合性能具有重要的工程应用意义。

齿轮齿面主动设计技术根据齿轮传动的功能需求来设计齿面形状，首先预置配对齿面的传动误差曲线以及最佳接触印痕，然后设计出能够精确满足以上预置条件的齿面及其加工方法，达到主动设计的目的。国内外学者在这方面做了大量工作[1-6]，Litvin提出的局部综合法[1-3]可以预控参考点附近的啮合性能，但远离参考点的齿面性质无法控制，可能导致啮合迹线严重弯曲，齿面接触区畸变。曹雪梅等通过设计并控制弧齿锥齿轮齿面上三个啮合点以实现对齿面啮合性能的全程控制[4-5]。吴训成等提出的齿面主动设计方法[6]，给定传动误差的方程以及齿面印痕的轨迹进行齿面一阶、二阶参数设计，可直接设计配对齿面的接触迹线、接触椭圆长轴的大小，并可设计高阶加速度。但上述文献都只针对格里森制单面法加工，而针对双面法加工的摆线齿准双曲面齿轮齿面主动设计的报道则较少。苏进展等[7]、Shih[8]提出了基于ease-off和敏感度矩阵的弧齿锥齿轮及准双曲面齿轮的齿面优化设计方法，但对如何同时保证双侧齿面啮合效果并未进行讨论。并且机床调整参数对齿面的影响并非都是线性关系[9]，由敏感度矩阵进行齿面加工参数反求，存在一定误差。

1预置的啮合性能

1.1　预置的传动误差曲线

传动误差是引起振动和噪声的重要原因，大量研究[1-5,7]表明抛物线形传动误差曲线能够吸收由安装误差引起的线性误差，并保持传动误差曲线形状不变。因此，预置传动误差曲线为抛物线形，如图1所示，横坐标φ1为小轮转角，纵坐标Δφ2为传动误差，φ1N,φ1M,φ1P分别为啮入点N、参考点M和啮出点P的小轮转角，δTE为啮合转换点的传动误差，z1为小轮齿数，2π/z1为小轮单个啮合周期的转角。

图1　抛物线形传动误差曲线Fig.1　Parabolic transmission error curve

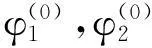
(1)

1.2　预置的接触印痕

齿面接触印痕的形状、大小及位置直接影响齿轮副的运动、润滑特性以及传动效率和承载能力。接触印痕的设计在大轮齿面的旋转投影面上完成，如图2所示，为减小齿面对安装误差的敏感性，将接触迹线设计为直线[10]，η为预置的接触迹线方向角，瞬时接触椭圆长轴大小按照接触区大小确定，一般将接触区选择在齿宽方向约40%～60%的位置。

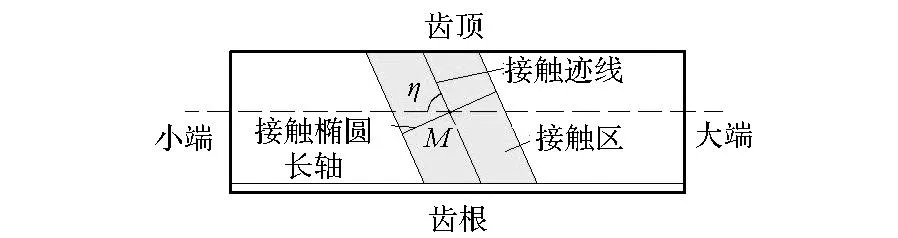
图2　接触印痕Fig.2　Contact pattern

2齿面主动设计

2.1　理论齿面

将运用调整卡初次计算得到的齿轮加工参数称为理论加工参数，由之加工的齿面称之为理论齿面，理论加工参数的获得可参考文献[11]。以展成法加工左旋小轮为例，如图3所示。

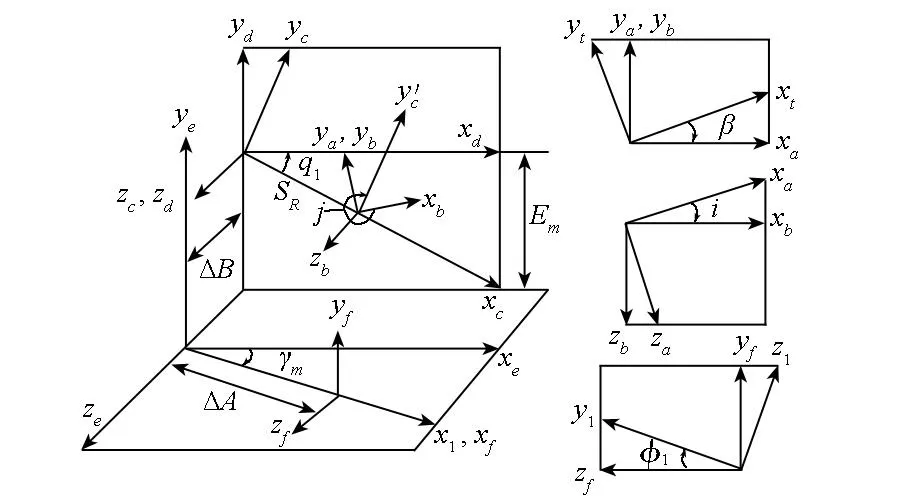
图3　左旋小轮加工坐标系Fig.3　Cutting coordinate systems of the left handed pinion

图3中,SR为刀位，i为刀倾角，j为刀转角，φ1为轮坯转角，β为刀盘转角，Em为垂直轮位，ΔB,ΔA分别表示床位和轮位修正量，γm为机床根锥角,q1=θc+φc,θc为初始摇台角,φc=φc2-φc1为摇台转角，φc2=φ1/Ra为展成运动对应的摇台转角，Ra为滚比，φc1=βz0/zp为摆线运动对应的摇台转角，z0和zp分别为刀齿组数和产形轮齿数。坐标系S1(x1,y1,z1)和St(xt,yt,zt)分别与小轮和刀盘固联，Sa,Sb,Sc,Sd,Se,Sf均为辅助坐标系。假设刀盘坐标系St中的刀刃方程rt(u)已知[12]：

rt(u)=rt(α0,rc,δ0,r0:u)

其中，u为刀具参数，α0为刀具齿形角，rc为刀刃圆弧半径，δ0为刀齿方向角，r0为刀齿半径。则小轮理论齿面的位矢rL和法矢nL可以表示为：

(2)

其中：

M1t=M1f(φ1)Mfa(ζ)Mat(β)

(3)

c11=cosγm[sin(θc+φc-j)cosicosβ-

cos(θc+φc-j)sinβ]-sinγmsinicosβ,

c12=cosγm[-sin(θc+φc-j)cosisinβ-

cos(θc+φc-j)cosβ]-sinγmsinisinβ,

c13=cosγmsinisin(θc+φc-j)+sinγmcosi,

c14=SRcosγmcos(θc+φc)-ΔA-sinγmΔB,

c21=sinφ1sinγm[sin(θc+φc-j)cosicosβ-

cos(θc+φc-j)sinβ]+cosφ1[cos(θc+φc-

j)cosicosβ+sin(θc+φc-j)sinβ]+

sinφ1cosγmsinicosβ,

c22=sinφ1sinγm[-sin(θc+φc-j)cosisinβ-

cos(θc+φc-j)cosβ]+cosφ1[-cos(θc+φc-

j)cosisinβ+sin(θc+φc-j)cosβ]-

sinφ1cosγmsinisinβ,

c23=sinφ1sinγmsinisin(θc+φc-j)+

cosφ1sinicos(θc+φc-j)-sinφ1cosγmcosi,

c24=SRsinφ1sinγmcos(θc+φc)-SRcosφ1sin(θc+

φc)+Emcosφ1+ΔBsinφ1cosγm，

c31=cosφ1sinγm[sin(θc+φc-j)cosicosβ-

cos(θc+φc-j)sinβ]+sinφ1[cos(θc+φc-

j)cosicosβ+sin(θc+φc-j)sinβ]-

cosφ1cosγmsinicosβ,

c32=cosφ1sinγm[-sin(θc+φc-j)cosisinβ-

cos(θc+φc-j)cosβ]+sinφ1[-cos(θc+φc-

j)cosisinβ+sin(θc+φc-j)cosβ]+

cosφ1cosγmsinisinβ,

c33=cosφ1sinγmsinisin(θc+φc-j)+

sinφ1sinicos(θc+φc-j)+cosφ1cosγmcosi,

c34=SRcosφ1sinγmcos(θc+φc)-SRsinφ1sin(θc+

φc)+Emsinφ1-ΔBcosφ1cosγm,

c41=c42=c43=0,c44=1；ζ=(i,j,θc,SR,Em,ΔA,ΔB,γm,Ra,α0,rc,δ0,r0)表示加工参数，包括机床设置以及刀盘参数。

对于展成法加工的小轮，理论齿面的获得还需借助于产形轮和被加工齿轮的啮合方程：

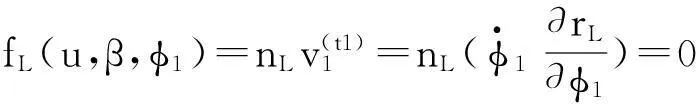
(4)

r2(u,β,φ2)=M2f(φ2)Mft(β)rt(u)

(5)

若大轮由展成法加工，则有：

(6)

若大轮由成形法加工，则有：

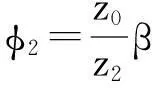
(7)

将式(6)或式(7)带入式(5)，得到化简后的大轮理论齿面为：

r2(u,β)=M2t(β)rt(u)

(8)

2.2　共轭齿面

在啮合坐标系中，以大轮理论齿面作为产形轮齿面展成小轮，如图4、图5所示。图4中H1,H2分别为小轮和大轮的齿顶距，V为偏置距，Σ为轴交角，S2(x2,y2,z2)固联于大轮坐标系，Sp,Sq,Sr,Ss为辅助坐标系。为获得与大轮理论齿面完全共轭的小轮共轭齿面，在展成过程中，应遵循式(9)所示的运动关系并满足啮合方程式(10)。

图4　啮合坐标系Fig.4　Mesh coordinate systems

图5　大轮展成小轮Fig.5　Pinion generated by gear

(9)

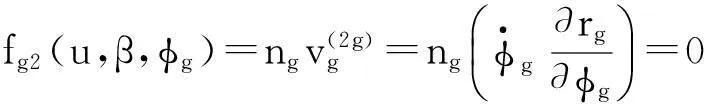
(10)

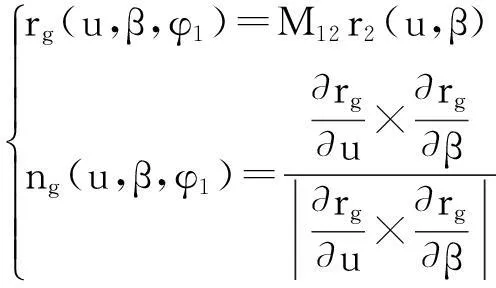
(11)

其中：

M12=M1s(V,Σ,H1,H2,φ1)Ms2(φ2)

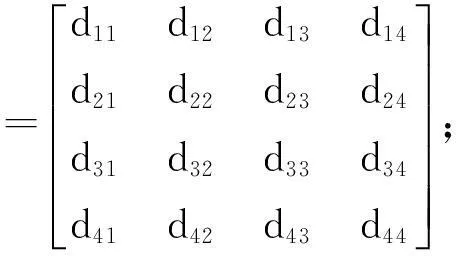
(12)

d11=cosΣ,d12=-sinφ2sinΣ,d13=cosφ2sinΣ,

d14=-H1-H2cosΣ,d21=sinφ1sinΣ,

d22=cosφ1cosφ2+cosΣsinφ1sinφ2,

d23=cosφ1sinφ2-cosΣcosφ2sinφ1,

d24=Vcosφ1-H2sinφ1sinΣ,d31=-cosφ1sinΣ,

d32=cosφ2sinφ1-cosΣcosφ1sinφ2,

d33=sinφ1sinφ2+cosΣcosφ1cosφ2,

d34=Vsinφ1+H2cosφ1sinΣ,

d41=d42=d43=0,d44=1。

联立式(8)、式(9)、式(10)、式(11)、式(12)，求解得到小轮共轭齿面Σg。

2.3　小轮目标齿面

完全共轭的配对齿面在各个啮合位置传动误差均为0，但这种齿面没有任何可调性, 制造和安装误差、承载变形都会造成齿面载荷集中而使轮齿破坏，因此实际应用中常常将配对齿面设计为点接触的具有二阶抛物线形或更高阶传动误差的齿面。由于小轮齿数较少，一般只针对小轮齿面进行设计。

为了使大小轮在啮合时满足预置的传动误差曲线，将大轮展成小轮共轭齿面时的运动关系式(9)用式(1)代替,则所得到的新齿面Σt与大轮线接触，且满足预置的传动误差函数Δφ2(φ1)，齿面Σt的位矢rt和法矢nt可表示为：

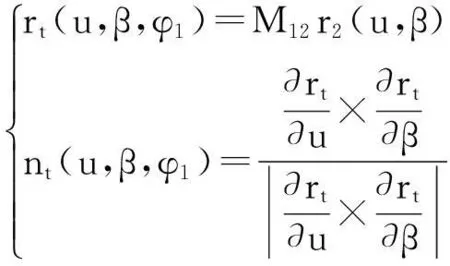
(13)

大轮旋转投影面上预置的接触迹线在大轮理论齿面、小轮共轭齿面Σg和齿面Σt上都对应唯一一条接触迹线，为了获得满足预置的接触区且与大轮在任意啮合位置点接触的齿面，首先根据配对齿面在啮合点处位矢的关系求得齿面Σt上的接触迹线NMP，如图6所示，Δφ2(φ1N),Δφ2(φ1M),Δφ2(φ1P)为对应点N,M,P处的传动误差，Δφ2(φ1M)=0。

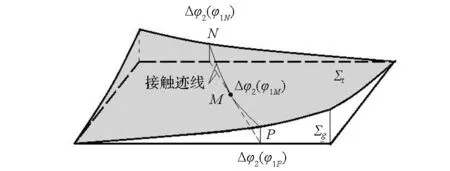
图6　齿面ΣtFig.6　Tooth surface Σt

然后将齿面Σt沿各个接触点的啮合线方向进行三段抛物线修形以控制接触区，修形曲线的顶点在曲线NMP上，如图7所示。在设计的接触区EFGH内，沿啮合线方向按照图8所示抛物线I进行修形，在啮合区外(AEHD和FBCG内)，沿啮合线方向按照抛物线II进行修形，即在啮合区外多去除一部分材料，最终得到小轮目标齿面Σ1。图8中：yI,yII方向为Σt面法线方向n1；x方向为指向轮齿大端的椭圆长轴方向。

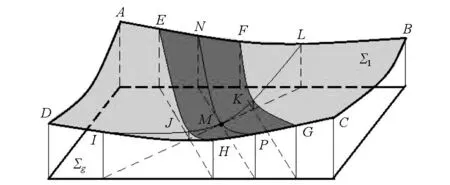
图7　小轮目标齿面Fig.7　Target tooth surface of pinion

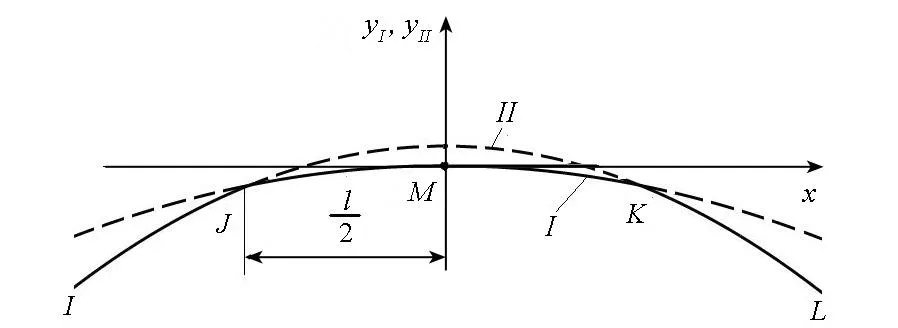
图8　接触线修形曲线Fig.8　Modification curves of contact line

啮合线方向修形所用抛物线I和II的方程为：

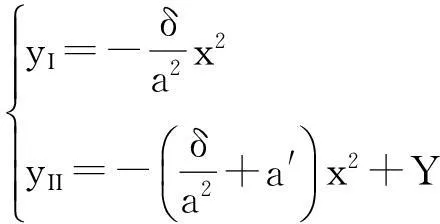
(14)

其中，a为预置的瞬时接触椭圆长半轴长度。δ为弹性变形量(一般取δ=0.006 35mm)，Y=a′l2/4为两抛物线顶点距离，l=2a，a′用来控制接触区外修形量。由于抛物线I与II在关于参考点M对称的点J和点K相交，则沿啮合线方向的法向修形量δy为：

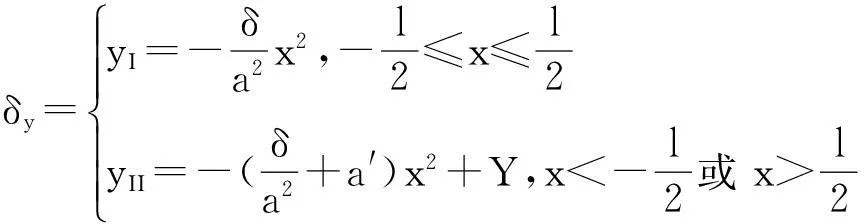
(15)

将齿面Σt离散为q个网格点(q=m×n，m,n分别表示沿齿高方向和齿宽方向的网格点数目，取m=n=15)，则对应的小轮目标齿面Σ1上网格点k(k=1,2,…,q)处的位矢r1和法矢n1可以表示为：

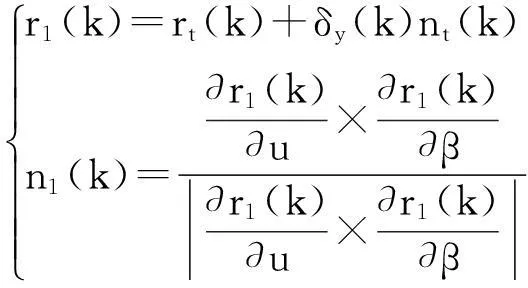
(16)

2.4　小轮理论齿面与目标齿面的偏差

小轮理论齿面ΣL、共轭齿面Σg与目标齿面Σ1在参考点M处相切，因此小轮理论齿面与目标齿面在网格点k处的法向偏差δ1L(k)为：

δ1L(k)=[r1(k)-rL(k)]nL(k)

(17)

3小轮加工参数反求

通过调整小轮理论齿面加工参数使其逼近目标齿面，由于预置的传动误差曲线为二次抛物线形，故引入3阶滚比修正运动，即将展成运动中的摇台转角φc2表示为关于小轮转角φ1的3阶多项式，如式(18)所示。

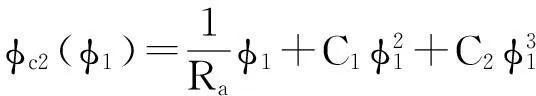
(18)

以小轮加工参数调整量Δζ(不含滚比Ra的机床设置参数、刀盘参数以及多项式系数C1,C2)为变量，以小轮齿面与目标齿面在各网格点法向偏差平方和最小为目标，由于摆线齿准双曲面齿轮采用双面法加工，因此机床设置的调整对两侧齿面都有影响，为同时兼顾两侧齿面的啮合性能，建立如式(19)所示的优化模型：

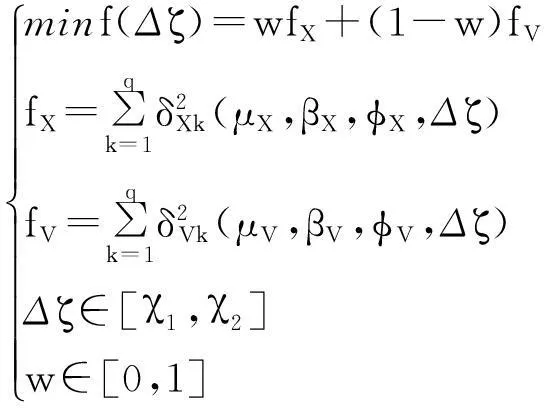
(19)

角标X和V分别表示凸面和凹面, χ1,χ2为各个加工参数调整量的上下限，均取[-1,1]。w为权重系数，可根据齿轮副实际工况中正转和反转工作时长比来确定。采用SQP法求解即可得到小轮加工参数调整量Δζ。

4算例验证

以某高速车桥齿轮副为例，大小轮基本参数、理论齿面机床设置、刀盘参数以及预置参数分别见表1、表2、表3和表4，工作面为小轮凹面和大轮凸面：

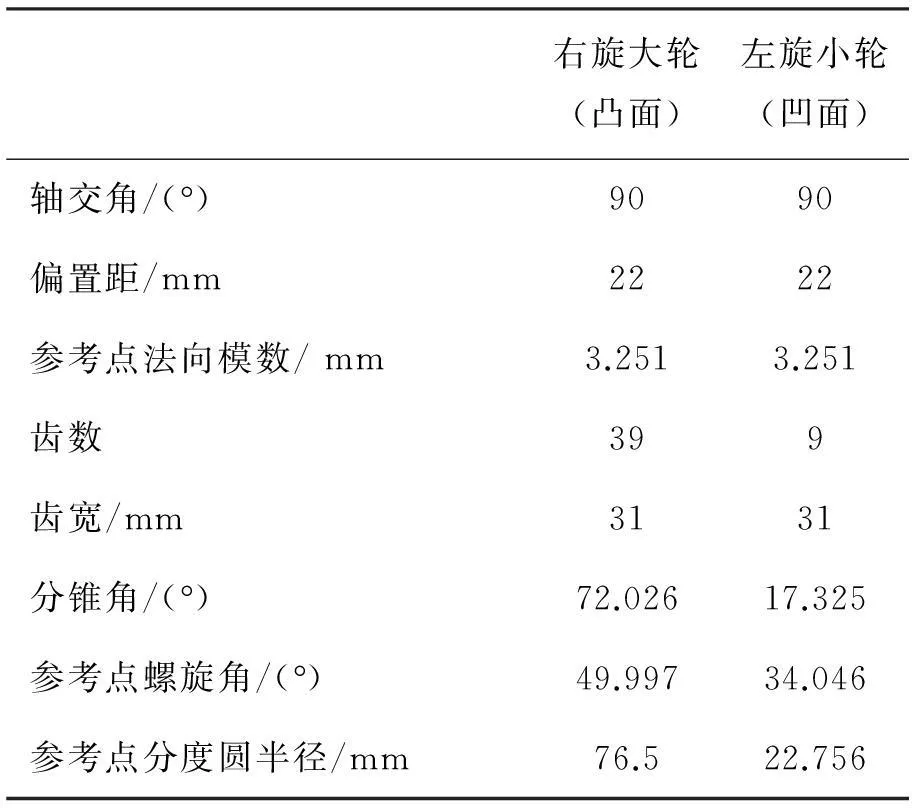
表1　基本参数

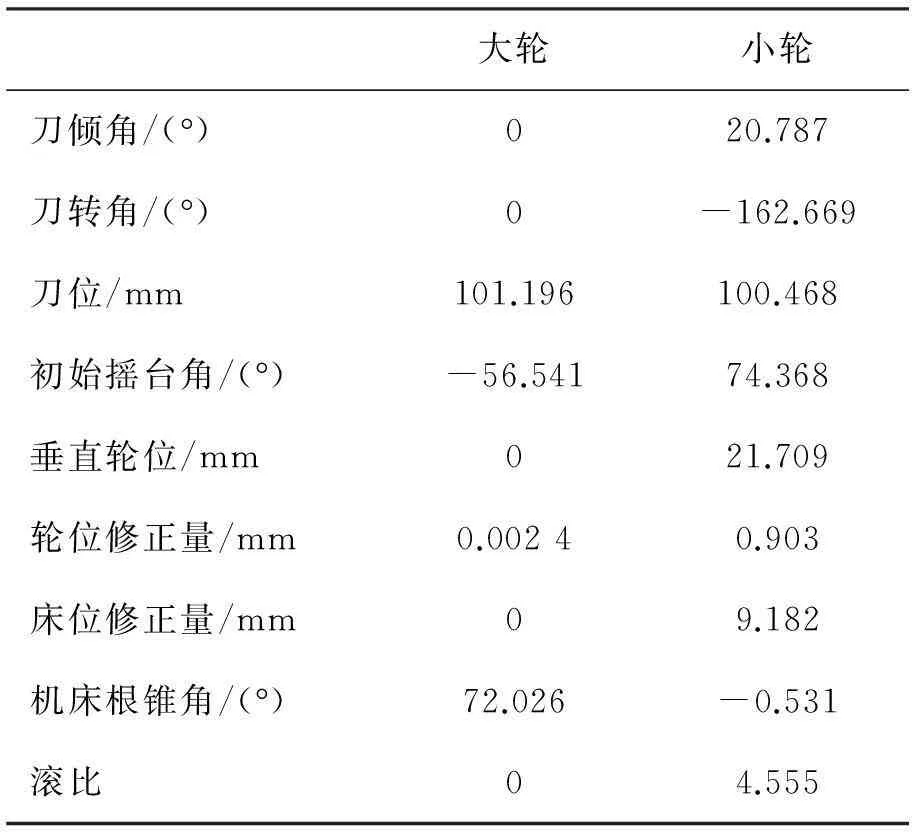
表2　机床设置

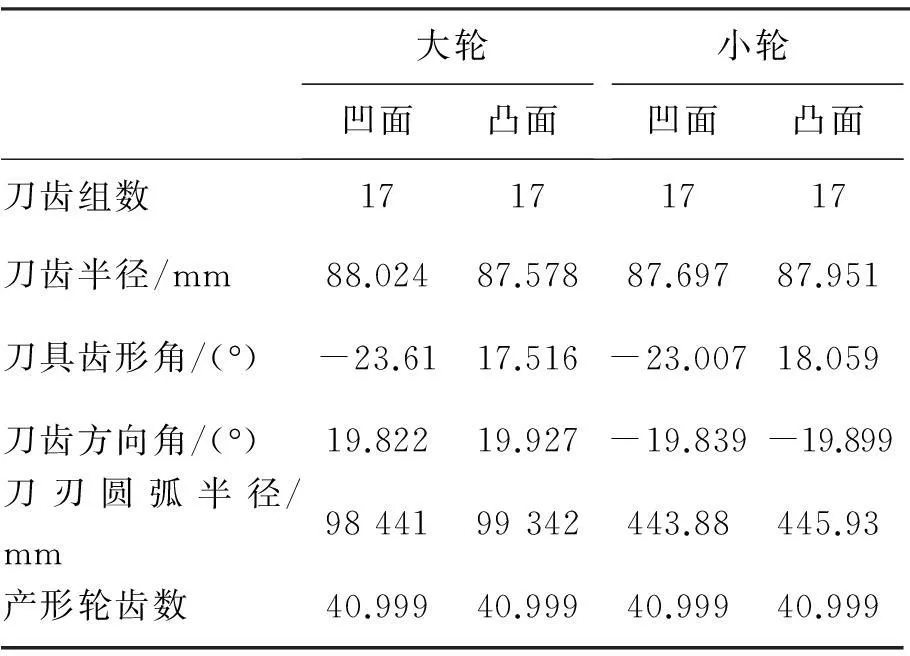
表3　刀盘参数

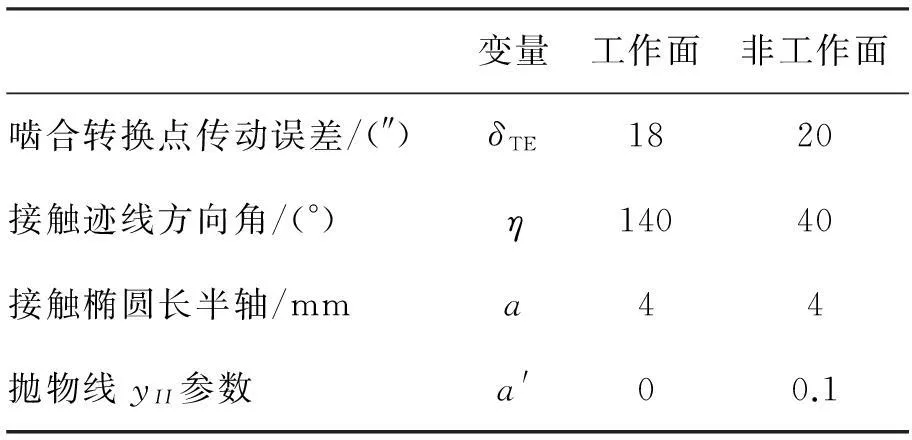
表4　预置参数

由理论加工参数得到的大小轮理论齿面如图9所示。

(a) 大轮　　　　　　　　　 (b) 小轮(a) Gear　　　　　　　　　(b) Pinion图9　大小轮理论齿面Fig.9　Theoretical tooth surfaces of gear and pinion

用大轮理论齿面展成小轮共轭齿面，并将其沿接触迹线方向和啮合线方向分别按照预置的抛物线曲线进行修形，得到的目标齿面相对于共轭齿面以及小轮理论齿面的偏差如图10和图11所示。

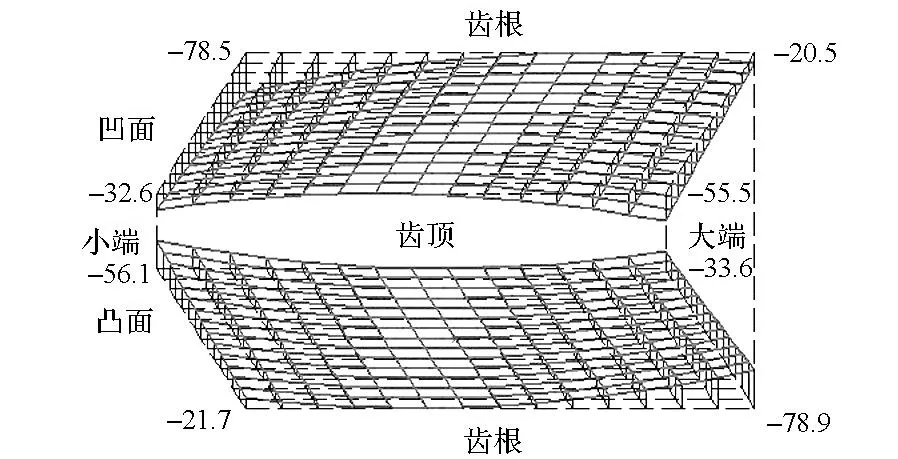
图10　小轮目标齿面与共轭齿面偏差Fig.10　Deviations between pinion target tooth 　　　surface and conjugate tooth surface

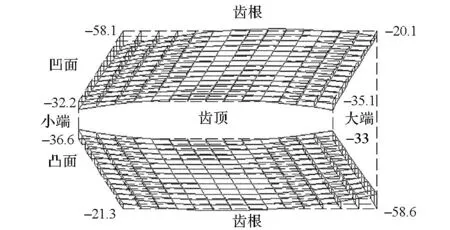
图11　小轮目标齿面与理论齿面偏差Fig.11　Deviations between pinion target tooth 　　　surface and theoretical tooth surface

当w取值分别为0.8，0.5，0.2时，求解式(19)优化模型得到对应的小轮加工参数调整量，见表5(篇幅所限，只列出w=0.5时的调整量)，加工参数调整后的小轮齿面与目标齿面的法向偏差如图12所示。

不同权重系数齿面逼近程度见表6。

比较可知，w=0.5时两侧偏差平方和最小，随着w增大，凸面最大偏差绝对值减小，凹面的则增大，反之亦然，即通过调整权重系数的大小，

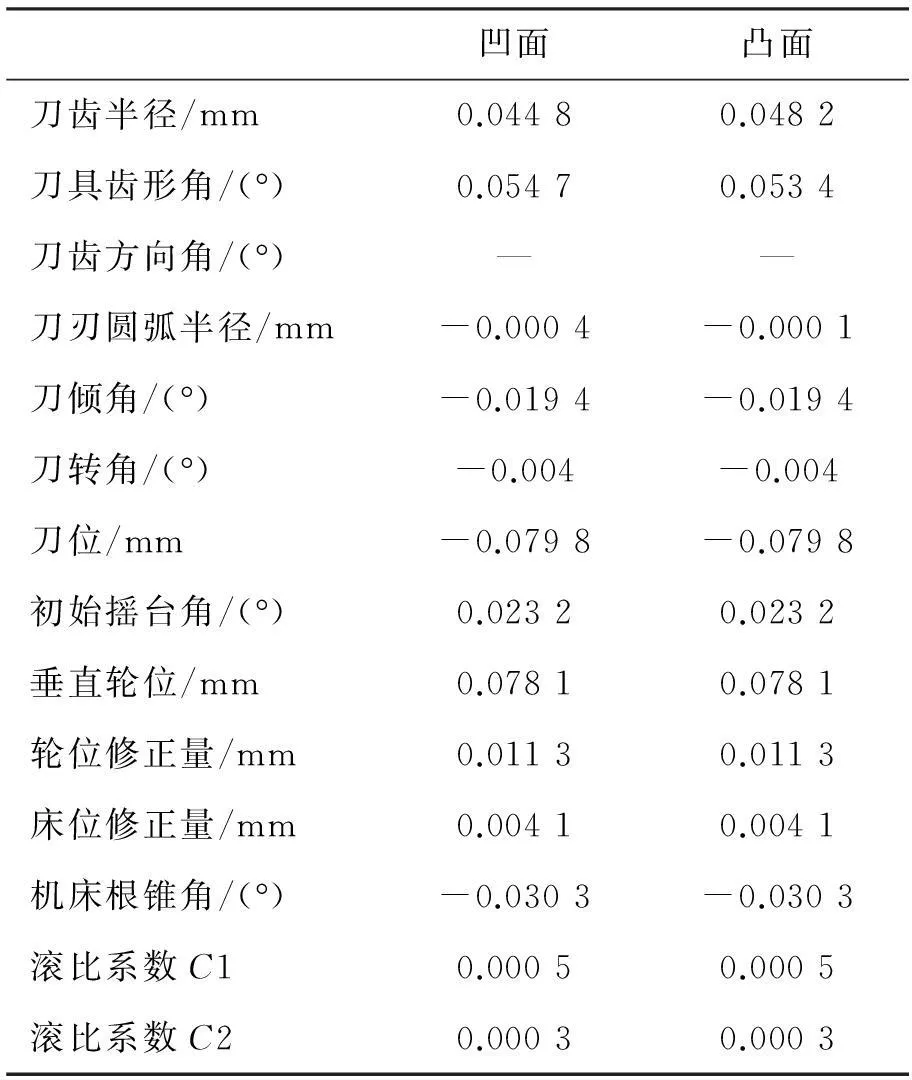
表5　小轮加工参数调整量

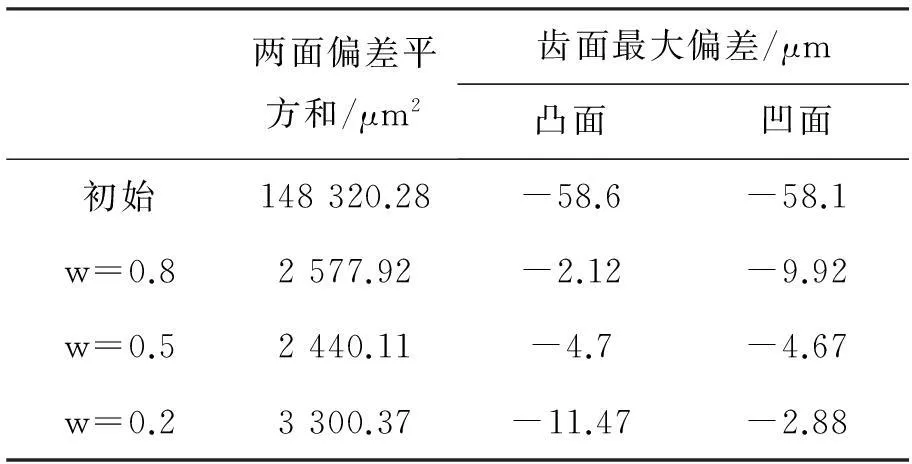
表6　不同权重系数比较

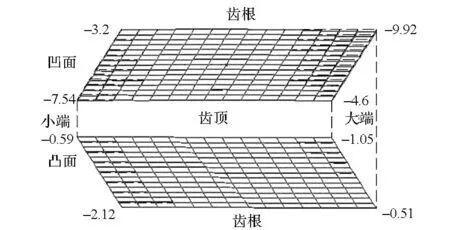
(a) w=0.8

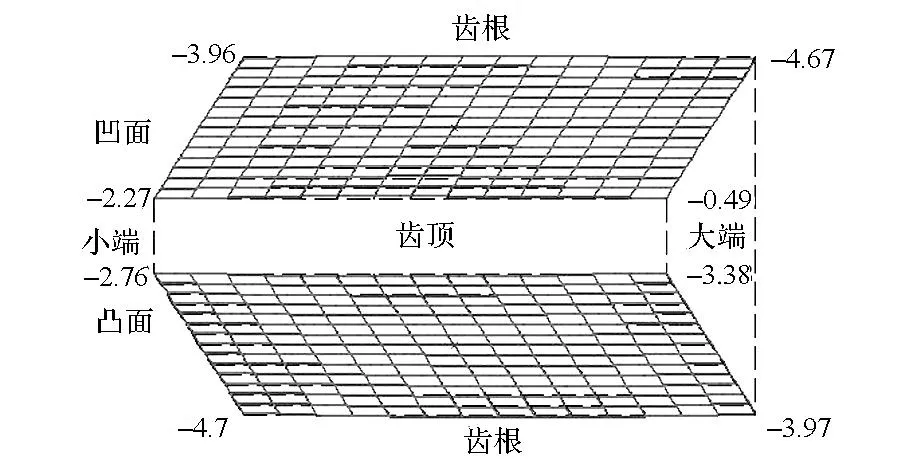
(b) w=0.5

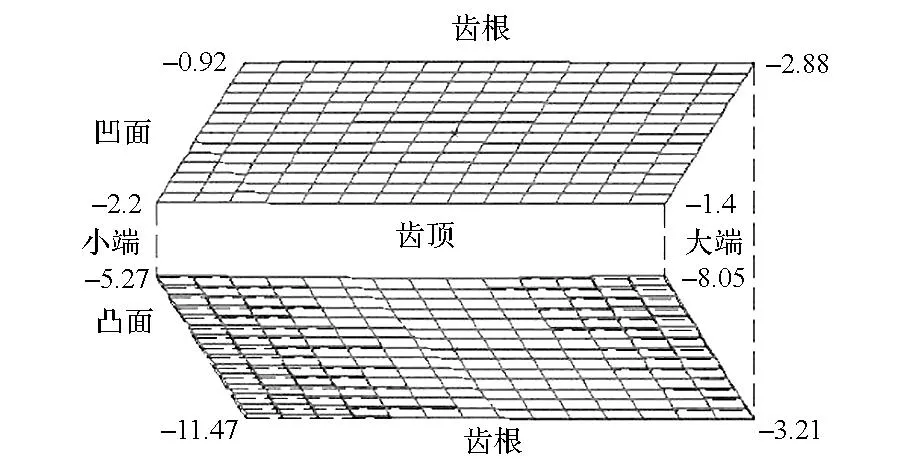
(c) w=0.2图12　小轮齿面与目标齿面的法向偏差Fig.12　Deviations between pinion tooth surface and target tooth surface

可以选择性地保证某一侧齿面与目标齿面的逼近程度，进而保证该侧啮合性能更加趋近预置条件。下面仅以w取0.5时为例，分析加工参数调整之后的小轮齿面与大轮理论齿面的啮合性能。TCA结果如图13所示，图13(a)和图13(c)中的虚线为预置的接触迹线。图14所示为两侧实际啮合点偏离预置接触迹线的距离,规定偏大端方向为正。啮合点序号按照进入啮合到退出啮合顺序排列。

经过比较，加工参数调整后大轮凸面和凹面的接触迹线偏离预置接触迹线最远距离分别为0.275mm和0.177mm，凸面接触印痕分布在齿宽方向36%～66.3%区域，凹面接触印痕分布在齿宽方向34.9%～72.1%区域，接触区未发生畸变。工作面和非工作面转换点处的传动误差值为19.2″和20.8″，分别与预置值相差6.67%和4%，基本达到了预置的啮合性能要求，故认为本方法可行。

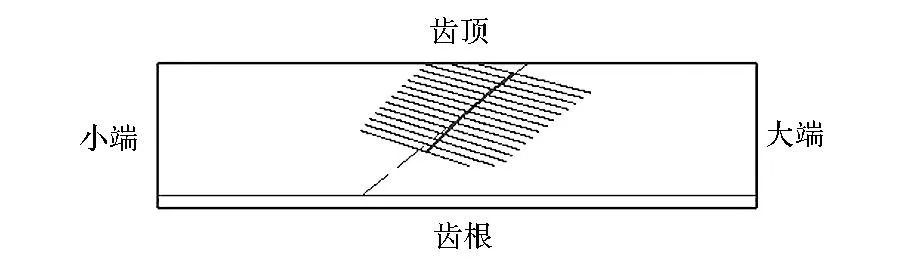
(a)大轮凸面接触印痕(a)Contact pattern for gear convex

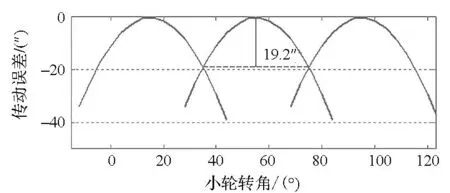
(b)工作面传动误差(b)Transmission error for drive side

(c)大轮凹面接触印痕(c)Contact pattern for gear concave

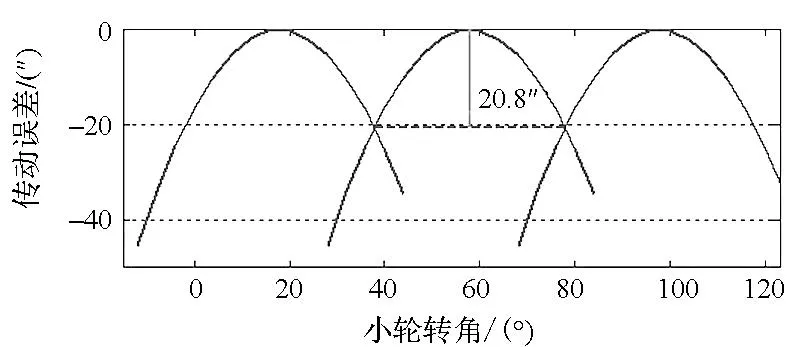
(d)非工作面传动误差(d) Transmission error for coast side图13　TCA结果Fig.13　TCA results

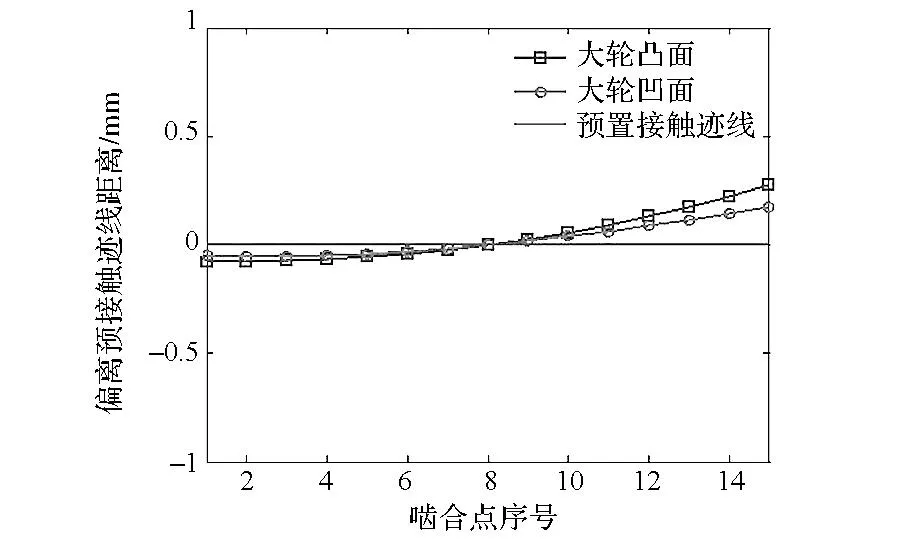
图14　偏离距离Fig.14　Deviations

5结论

对小轮共轭齿面沿接触迹线方向与啮合线方向进行双向修形获得了满足预置传动误差曲线以及接触印痕的小轮目标齿面；建立了小轮齿面与目标齿面法向偏差平方和最小优化模型，并运用SQP法求解得到高度逼近目标齿面的小轮齿面加工参数调整量；通过改变权重系数，可以选择性地保证某一侧齿面的啮合性能，如加装了缓速器的卡车，在设计时应该适当增加反车面权重系数，避免反车面过早失效；该设计方法使得设计人员能够按照齿轮传动的性能需求来设计齿面形状，经过推广，同样适用于其他类型齿轮传动；进一步研究方向应该为高阶传动误差设计。

参考文献(References)

[1]Litvin F L, Zhang Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears[R]. NASA CR4342, Chicago,USA: NASA Lewis Research Center, 1991.

[2]Litvin F L. Gear geometry and applied theory[M]. USA: Prentice Hall, 1994.

[3]赵宁,秋朋园,刘贵立.高重合度人字齿轮轮齿最佳修形优化设计[J].国防科技大学学报,2015,37(1): 165-170.

ZHAO Ning,QIU Pengyuan,LIU Guili.Modification optimization of double helical gears with high contact ratio[J]. Journal of National University of Defense Technology,2015,37(1):165-170.(in Chinese)

[4]Cao X M, Fang Z D, Xu H,et al. Design of pinion machine tool-settings for spiral bevel gears by controlling contact path and transmission errors[J].Chinese Journal of Aeronautics,2008,21(2): 179-186.

[5]曹雪梅,方宗德,张金良,等.弧齿锥齿轮的齿面主动设计[J].机械工程学报,2007,43(8): 155-158.

CAO Xuemei, FANG Zongde, ZHANG Jinliang, et al. Function-oriented active tooth surface design of spiral bevel gears[J].Journal of Mechanical Engineering,2007,43(8): 155-158.(in Chinese)

[6]吴训成,毛世民,吴序堂. 点啮合齿面主动设计研究[J]. 机械工程学报，2000, 36(4):70-72.

WU Xuncheng, MAO Shimin, WU Xutang. On function-oriented design of point contact tooth surfaces[J]. Journal of Mechanical Engineering, 2000, 36(4):70-72.(in Chinese)

[7]苏进展,贺朝霞.弧齿锥齿轮齿面的高精度修形方法[J].华南理工大学学报(自然科学版), 2014,42(4)： 91-96.

SU Jinzhan,HE Zhaoxia.High-precision modification of tooth surface for spiral bevel gears[J].Journal of South China University of Technology(Natural Science Edition), 2014, 42(4)： 91-96.(in Chinese)

[8]Shih Y P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears[J]. Mechanism and Machine Theory,2010, 45(8): 1108-1124.

[9]唐进元,曹康,李国顺,等. 机床调整参数误差对小轮齿面误差影响规律的理论研究[J]. 机械工程学报，2010, 46(17): 179-185.

TANG Jinyuan, CAO Kang, LI Guoshun, et al. Research on the effect law between machine setting parameter errors and hypoid gears surface errors[J]. Journal of Mechanical Engineering, 2010, 46(17) : 179-185.(in Chinese)

[10]Litvin F L,Fuentes A, Hayasaka K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J].Mechanism and Machine Theory, 2006, 41(1): 83-118.

[11]董学朱.摆线齿锥齿轮及准双曲面齿轮设计和制造[M].北京:机械工业出版社,2002:335-336.

DONG Xuezhu. Design and manufacturing of cycloid bevel gear and hypoid gear[M]. Beijing: China Machine Press, 2002 :335-336.(in Chinese)

[12]Vimercati M. Mathematical model for tooth surfaces representation of face-hobbed hypoid gears and its application to contact analysis and stress calculation[J]. Mechanism and Machine Theory, 2007, 42(6): 668-690.

http://journal.nudt.edu.cn

Active tooth surface design of cycloid hypoid gears

DUJinfu1,2,FANGZongde1,ZHANGYongzhen1,LIJianhua1

(1. College of Mechanical Engineering, Northwestern Polytechnical University, Xi′an 710072, China;

2. School of Mechanical and Precision Instrument Engineering, Xi′an University of Technology, Xi′an 710048, China)

Abstract：In order to pre-control the meshing performance of cycloid hypoid gears, a conjugate pinion tooth surface was generated by gear theoretical tooth surface. The pinion target tooth surface that meets the preconditions was obtained by modifying the conjugate tooth surface along the contact path and the contact line. The sum of tooth surface normal square errors between pinion theoretical and target tooth surface was calculated. The optimal model was built, setting the modifications of pinion machining parameters as variables and the least sum of square errors between pinion tooth surface and pinion target tooth surface on both sides as object. This optimization model was solved via sequence quadratic program. The validity of this modification method was demonstrated by using a numerical example of a high speed axle gear pair. The results show that the max normal errors on both sides are -4.7μm and -4.67μm, the transmission error deviations are 6.67% and 4%, the max contact path deviations are 0.275 mm and 0.177 mm, the results are found in line with the preconditions.

Key words：duplex; cycloid tooth; active design; modification; sequence quadratic program

中图分类号：TH132

文献标志码：A

文章编号：1001-2486(2015)06-167-08

作者简介：杜进辅(1984—)，男，甘肃白银人，博士研究生，E-mail：robin367@qq.com；万宗德(通信作者)，男，教授，博士，博士生导师，E-mail:fauto@nwpu.edu.cn

基金项目：国家自然科学基金资助项目(51175423，51375384)

收稿日期：*2015-01-06

doi:10.11887/j.cn.201506030