考虑实测载荷谱的斜齿轮减振修形设计

贾超，方宗德，姚立纲，张俊，卢宗兴

(1.福州大学机械工程及自动化学院，福建福州，350116；2.西北工业大学机电学院，陕西西安，710072)

大量研究和长期实践表明，齿面修形可以减小齿轮传动系统的振动和噪声、减小齿面载荷、降低齿面闪温，是改善齿轮传动性能的有效措施因此，齿面修形一直是齿轮传动研究领域的热点，在齿轮设计和制造中始终占有重要地位。

LITVIN 等[1]结合轮齿接触分析(tooth contact analysis，TCA)技术对齿轮进行了三维拓扑修形，并应用商用有限元软件研究了负载时的轮齿弯曲应力、接触应力和齿面载荷分布情况；WAGAJ等[2−3]分析了齿面修形对齿轮副接触应力和磨损的影响，认为通过合理的修形设计可以减小应力和磨损；BRUYÈRE 等[4]研究了传动误差最小的窄齿面圆柱齿轮的齿廓修形设计简化方法，并通过与解析法计算结果的对比验证了简化方法的合理性；李晓贞等[5]研究了面齿轮传动系统中的圆柱齿轮齿面修形技术，通过齿面修形设计改善了面齿轮传动系统的动态性能；贾超等[6]基于TCA和轮齿承载接触分析(loaded tooth contact analysis，LTCA)完成了高速内啮合人字齿轮的多目标优化修形；魏静等[7]研究了考虑修形的斜齿轮传动系统的非线性激励与动力学特性；WANG等[8]分析了齿面三维修形对风电传动系统动力学性能的影响；SHEN 等[9]通过改变刀具齿廓形状和预设几何传动误差完成了面齿轮的三维修形；林腾蛟等[10]以海洋平台升降齿轮箱为对象，研究了修形前后多级行星齿轮箱在复杂激励作用下的振动噪声；张俊等[11]为了抑制系统的振动和噪声，以动态传动误差波动量为指标，研究了斜齿行星轮系的修形策略；杨硕文等[12]构建了一种直齿轮复合修形设计方法，并通过算例验证了提出的复合修形设计方法的有效性；XU 等[13]建立了行星轮的齿面修形模型，并基于此分析了修形参数对行星轮系时变啮合刚度、传动误差、接触印痕和动态响应的影响；WANG 等[14]建立了考虑齿背接触特性的电动汽车行星轮系非线性振动模型，并在此基础上研究同时考虑齿面、齿背接触状态的齿面减振修形优化；HUANGFU等[15]研究了齿面磨损条件下修形对薄壁齿轮动态特性的影响；WANG 等[16]基于轮齿接触分析、轮齿承载接触分析和系统动态分析，研究了斜齿轮齿面三维修形对齿轮传动系统动态啮合性能的影响。

通常，齿轮所受载荷越大则变形越大，所需修形量越大，齿面修形参数的设计与齿轮所受载荷密切相关。上述文献研究大多基于某一载荷进行齿面修形设计，然而，在实际工况中，齿轮所受载荷复杂多变，如机车运行过程中需要提速、减速和紧急制动等[17]。齿面修形设计如何兼顾常用载荷和运转过程中的其他载荷是齿面修形设计研究中亟待解决的问题。本文基于载荷谱，设计一个当量载荷作为齿面修形的设计载荷进行齿面修形优化设计，兼顾了工作载荷范围中最常用载荷和其他载荷下的齿轮副啮合性能改进，为齿面修形设计在工程中的应用提供了一种新思路。

1 基于载荷谱的当量载荷设计

基于载荷谱中的载荷出现概率和载荷，设计当量载荷作为齿面修形的设计载荷。出现概率为频次与小轮总旋转转数的比值(频次为齿轮传动系统测试期间此转矩出现的小轮旋转转数)。出现概率最大的载荷为最常用载荷。

当量载荷被设计为

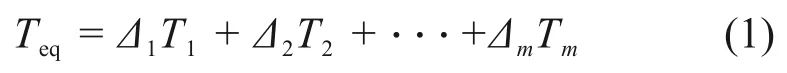
式中：Teq为设计当量载荷；Δi(i=1，…，m)为载荷的出现概率；Ti(i=1，2，…，m)为载荷谱中的载荷。

2 承载传动误差和啮入冲击力计算

齿轮减振降噪技术通过减少激励和降低响应来抑制齿轮传动中的振动，其中，减少激励是最根本措施。大量理论和试验研究表明，齿轮传动误差和啮合冲击是首要内激励源，齿面修形的直接目标就是减少传动误差和啮合冲击的激励作用。

本文通过TCA 和LTCA 得到轮齿法向位移等[18−19]，将轮齿法向位移转化为啮合线上位移，并用转角表示承载传动误差。承载传动误差(loaded transmission error，LTE)和承载传动误差幅值(amplitude of loaded transmission error，ALTE)表示如下：

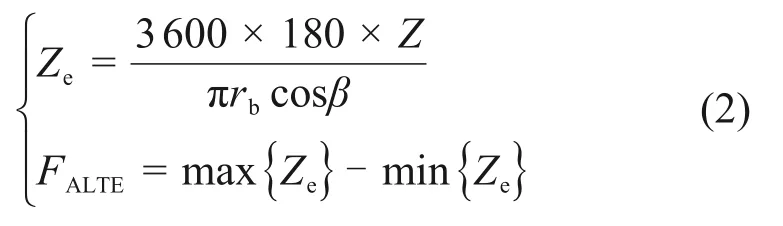
式中：Z为轮齿法向位移；Ze为承载传动误差；rb为大轮基圆半径；β为螺旋角；FALTE为承载传动误差幅值。

通过TCA 和LTCA 可以计算啮入点位置，基于转速和载荷可以进一步求得啮入冲击速度和冲击点啮合刚度，最后通过轮齿进入啮合瞬间的能量守恒原则计算啮入冲击力，具体啮入冲击力计算如下。

齿轮对的转动惯量和诱导质量分别为

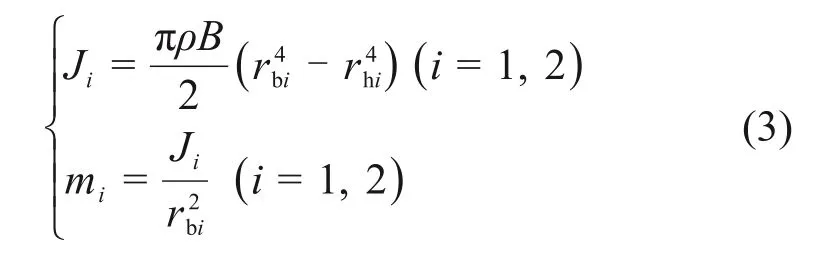
式中：J1和J2分别为小轮和大轮的转动惯量；ρ为齿轮材料密度；B为齿宽；rb1和rb2分别为小轮和大轮的基圆半径；rh1和rh2分别为小轮和大轮轮毂内孔半径；m1和m2分别为小轮和大轮的诱导质量。

齿轮进入啮合时，啮入点冲击动能为

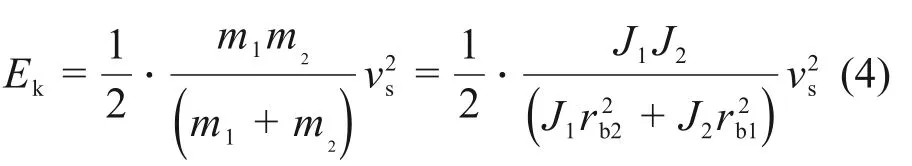
式中：Ek为啮入点冲击动能；vs为啮入冲击速度。

由于冲击作用，导致轮齿之间产生最大冲击变形量δs，与之相对应的冲击力Fs则为最大冲击力。根据冲击力学理论[20]，Fs可以表示为

式中：Ks为冲击点啮合刚度；δs为最大冲击变形量；n为变形系数，可通过数据拟合获得，本文取1.1。

弹性势能Ek可以表示为

根据能量守恒原则，冲击动能和弹性势能Ek有如下关系：

根据式(7)可以得到最大冲击变形量δs：

根据最大冲击变形量δs可以得到最大冲击力Fs：

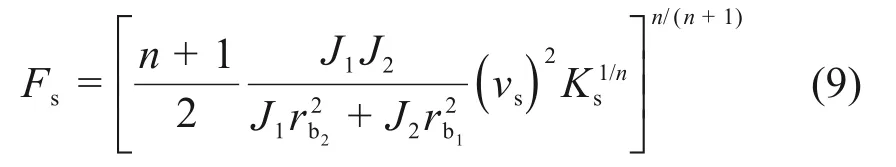
3 齿面优化修形

3.1 传统修形设计

图1所示为传统修形设计，由图1可见：齿廓和齿向修形曲线由2 段二阶抛物线和1 段直线组成。图中y1和y2分别为齿根和齿顶最大修形量，y3和y4分别为齿根和齿顶修形长度，y5和y6分别为齿向两端最大修形量和中间不修形区域长度。传统修形齿面可通过理论齿面与修形曲面叠加获得，详细构造方法可见文献[6]。

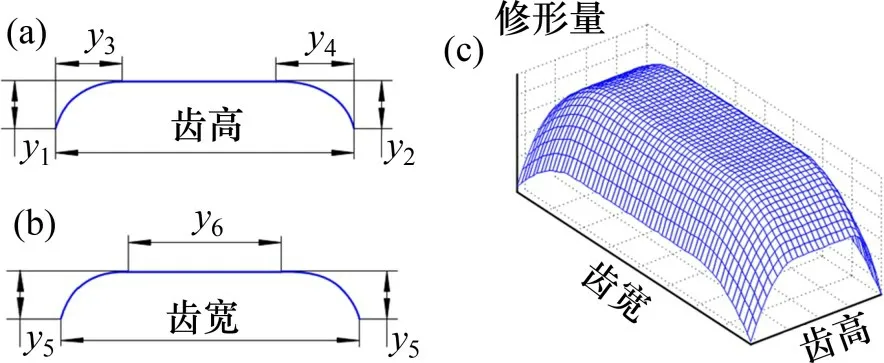
图1 传统修形设计Fig.1 Designation of traditional modification

3.2 基于重合度的改进修形设计

改进修形设计通过预设几何传动误差和齿向修形相结合的方式实现。图2所示为基于重合度的预设几何传动误差设计。由图2可见：预设的齿面几何传动误差与该对齿轮共轭齿面在设计载荷下的承载传动误差大小相等、方向相反。

预设几何传动误差可精确控制图2所示的“三齿”和“两齿”区域的修形量，实现ALTE的大幅下降。

图2 基于重合度的预设几何传动误差设计Fig.2 Designation of predesigned transmission error based on contact ratio

在常用修形类型中，齿向修形可以减小误差敏感性，避免偏载，减小齿端边缘效应，在齿面修形的实际应用中，齿向修形往往是必须的。在本研究中，加入齿向修形后可以减小啮入冲击力。图3所示为基于重合度的改进修形设计，由图3可见：基于预设几何传动误差修形的基础上，同时对齿轮齿面进行齿向修形，将同时减小ALTE和啮入冲击力。

图3 基于重合度的改进修形设计Fig.3 Designation of improved modification based on contact ratio

3.3 传统修形齿面优化模型及流程

优化变量：y1，y2，y3，y4，y5和y6。

目标函数：

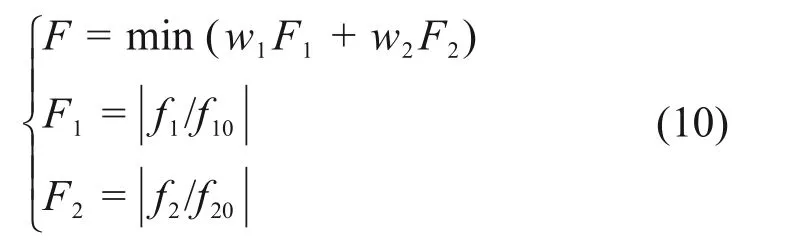
约束条件：

式中：f1和f10分别为修形齿轮和未修形齿轮的ALTE；f2和f20分别为修形齿轮和未修形齿轮的啮入冲击速度；w1和w2为权重因子，都取0.5；δmin和δmax分别为修形量的上界和下界；hmin和hmax分别为齿廓修形长度的上界和下界；lmin和lmax为齿向不修形长度的上界和下界。

3.4 改进修形齿面优化模型及流程

优化变量：ΔLi(i=1～k)，y5和y6。

目标函数：

约束条件：

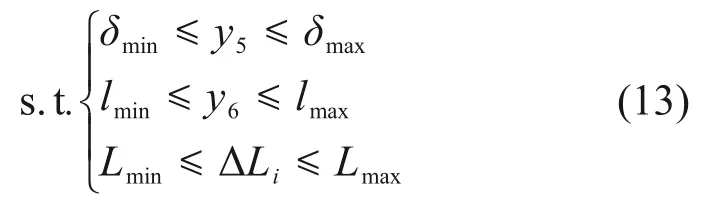
式中：k为将修形齿面连续加工过程离散后，刀具在走刀过程中的位置个数，其值等于TCA 计算中的接触线数量；Li(i=1～k)为刀具在每个位置的附加位移；w1和w2都取0.5。

图4(a)所示为传统修形的优化流程图。传统修形设计主要在齿根、齿顶以及齿向两侧区域进行修形，通过遗传算法获得优化的修形设计参数。图4(b)所示为改进修形的优化流程图。改进修形设计与传统修形设计不同，改进修形设计通过预设几何传动误差设计考虑了齿轮对重合度的影响，能够精确跟踪齿轮啮合传动中齿面上不同啮合区的修形需求，在齿根、齿顶、齿向两侧以及齿面中间区域都进行了修形，以此来实现ALTE的大幅下降，同时结合齿向修形的双向修形设计，实现ALTE和啮入冲击力的同时减小。

图4 齿面修形优化流程图Fig.4 Flowchart of optimization of tooth modification

4 算例与分析

本文算例只针对小齿轮修形。所用遗传优化算法的种群个数设置为50，进化代数设置为50，交叉概率设置为0.6，变异概率设置为0.1。表1所示为动车组所用齿轮箱斜齿轮副的基本参数[17]，其中小轮为左旋，大轮为右旋。表2所示为齿轮箱齿轮副的载荷谱。参考文献[17]中，作者采集了北京—上海运行区间动车组的实时运行速度信号，根据其采集到的信号，可知在运行区间内，小齿轮每趟约为1.1×106r，齿轮副的载荷谱有9 种工况，分别对应9种负载。

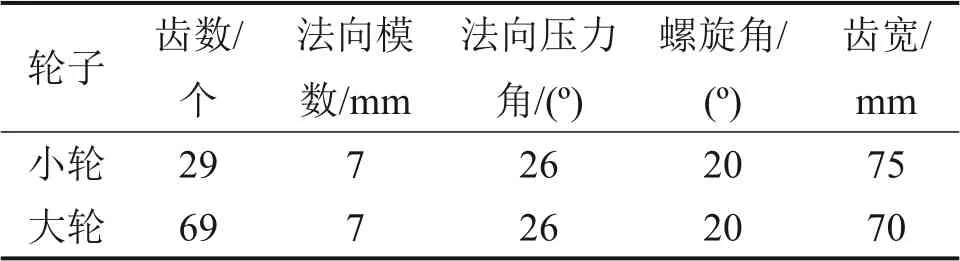
表1 齿轮副参数Table 1 Parameters of the gear-pair

根据式(1)和表2中的载荷谱，计算可得当量载荷为2 339 N·m。从表2可见：1 948 N·m为最常用载荷；1 884 N·m 和3 994 N·m 为最小荷载和最大载荷，也是出现概率较大的载荷。为了检验基于当量载荷的齿面修形是否兼顾到最常用载荷和其他载荷，下面考察修形齿轮副在2 339，1 948，1 884和3 994 N·m下的啮合性能。

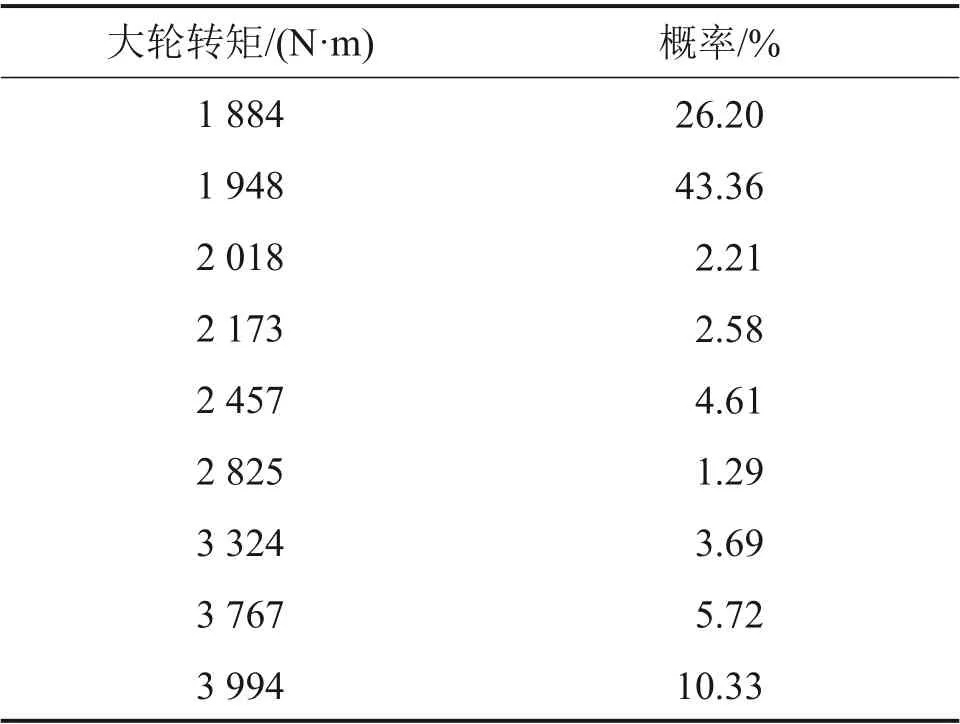
表2 载荷谱Table 2 Load spectrum

图5所示为设计载荷为2 339 N·m 时，传统修形和改进修形的修形量。图6所示为标准齿面和设计载荷为2 339 N·m时的传统修形和改进修形的接触印痕，从图5和图6可见：齿面修形后，齿面接触路径发生改变，避免边缘接触，这有助于改善齿轮副的啮合性能。

图5 设计载荷为2 339 N·m时的齿面修形量Fig.5 Tooth modification value at design load of 2 339 N·m

图6 标准齿面和设计载荷等于2 339 N·m时的修形齿面接触印痕Fig.6 Tooth contact pattern of standard tooth and modified tooth at design load of 2 339 N·m

图7所示为设计载荷等于2 339 N·m 时，当量载荷、最常用载荷以及2种较常用载荷下的标准齿面、传统修形和改进修形的ALTE 对比。由图7可见：传统修形和改进修形都可实现最常用载荷和较常用载荷下的ALTE 下降。表3所示为设计载荷等于2 339 N·m时，在不同载荷下，传统修形和改进修形的ALTE 下降比例。由表3可见：传统修形可在最常用载荷和较常用载荷下使ALTE下降30%以上；改进修形可在最常用载荷和较常用载荷下使ALTE下降40%以上。

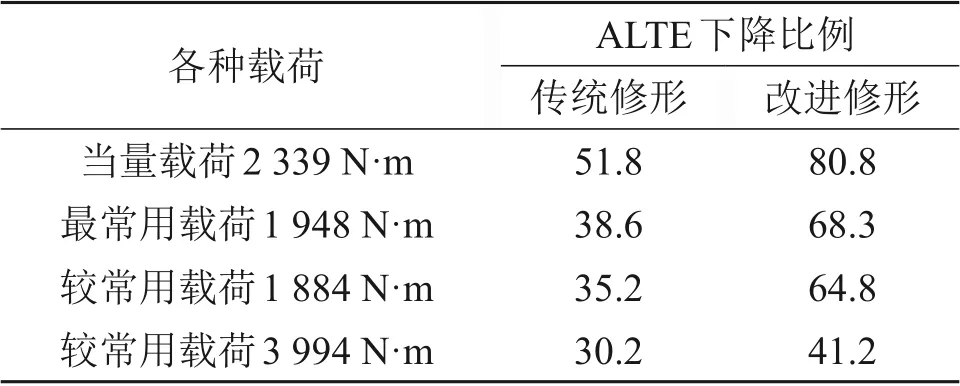
表3 设计载荷等于2 339 N·m时，齿面修形后各种载荷下的ALTE下降特征Table 3 Comparison of reduction characteristics of ALTE under various loads at design load of 2 339 N·m%

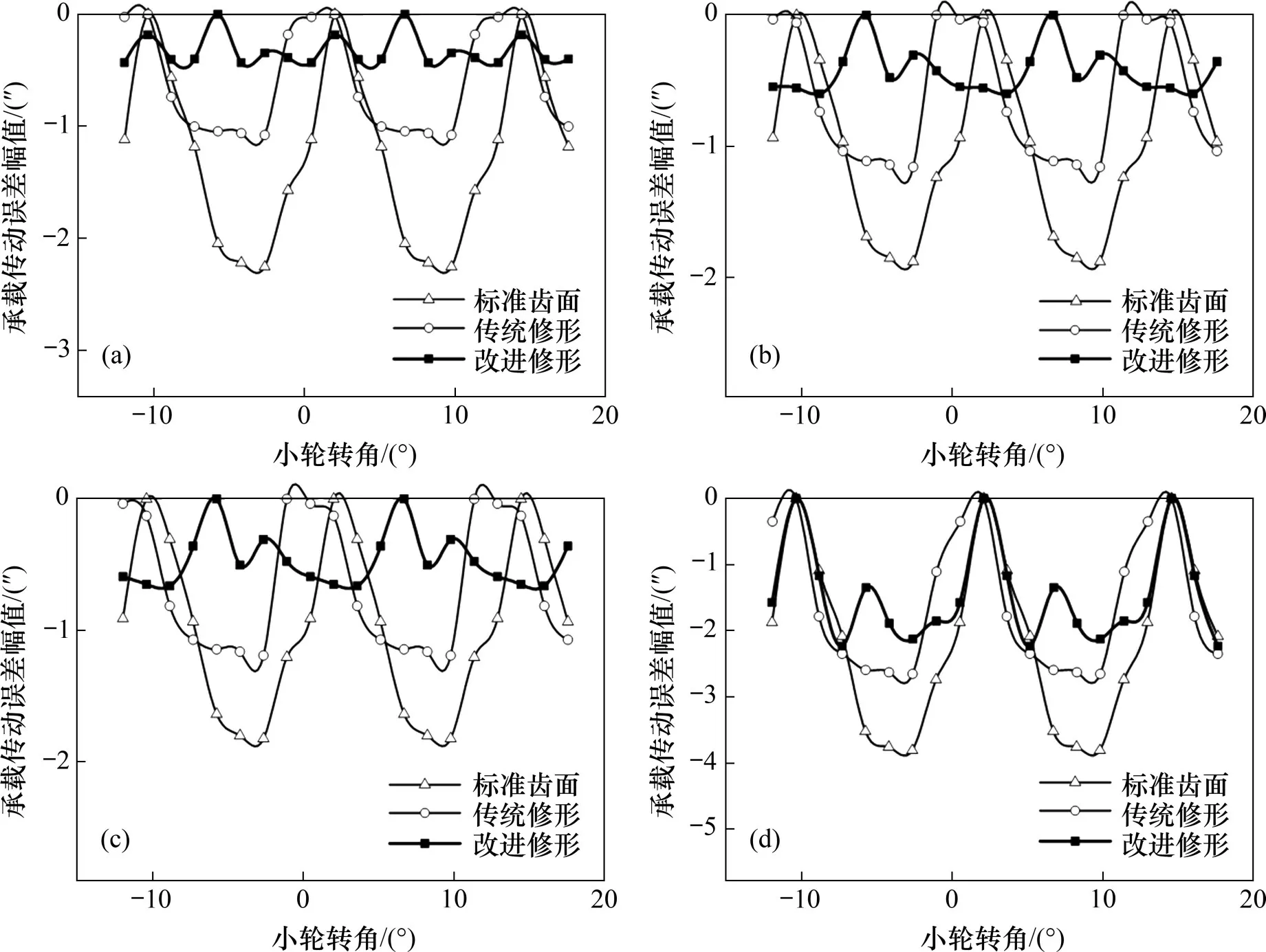
图7 设计载荷等于2 339 N·m时，当量载荷和工作载荷范围内其他载荷下的ALTE对比Fig.7 Comparison of ALTEs under equivalent load and other loads in working load range at design load of 2 339 N·m

图8所示为设计载荷等于2 339 N·m 时，标准齿面、传统修形和改进修形的ALTE 随载荷的变化。由图8可见：随负载增加，传统修形和改进修形的计算结果都呈现先减小后增大趋势；载荷等于当量载荷时，ALTE最小，载荷等于载荷谱中最常用载荷时，ALTE大幅下降；齿轮副在整个工作载荷范围的载荷下ALTE都出现较大幅度下降。与传统修形相比，改进修形显示了更大优势。

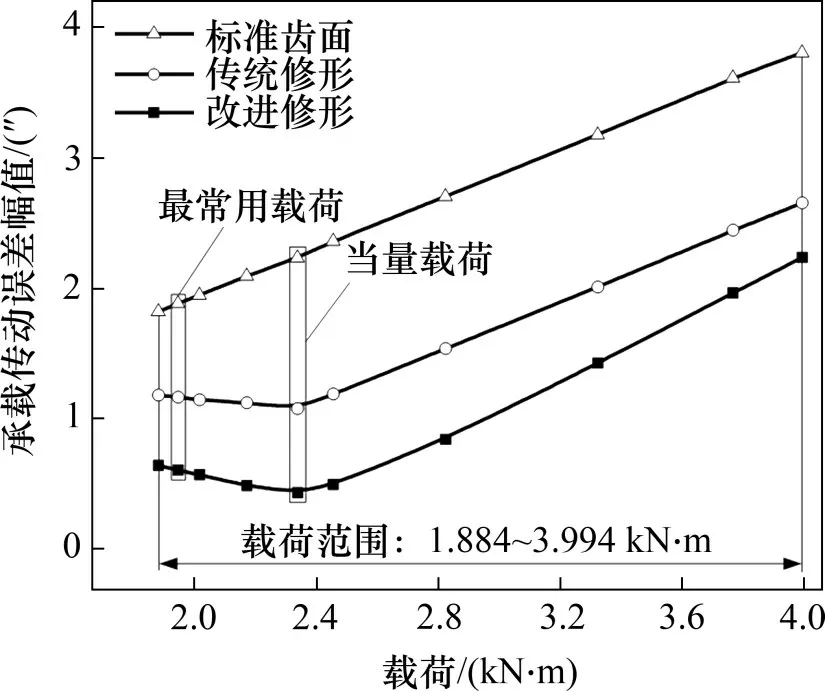
图8 设计载荷等于2 339 N·m时，3种齿面的ALTE随载荷的变化Fig.8 Variation of ALTEs of three types of tooth surfaces with load at design load of 2 339 N·m

图9所示为设计载荷等于2 339 N·m，小轮转速等于3 000 r/min时，当量载荷、最常用载荷以及工作载荷范围内其他较常用载荷下的标准齿面、传统修形和改进修形的啮入冲击力对比。由图9可见：传统修形和改进修形都可实现最常用载荷和较常用载荷下的啮入冲击力下降。表4所示为设计载荷等于2 339 N·m时，在不同载荷下，传统修形和改进修形的啮入冲击力下降比例。由表4可见：传统修形可在最常用载荷和较常用载荷下的使啮入冲击力下降40%以上，改进修形可在最常用载荷和较常用载荷下使啮入冲击力下降50%以上。

图9 设计载荷等于2 339 N·m时，当量载荷和工作载荷范围内其他载荷下的啮入冲击力对比Fig.9 Comparison of mesh-in impact forces under equivalent load and other loads in working load range at design load of 2 339 N·m

表4 设计载荷等于2 339 N·m时，齿面修形后各种载荷下的啮入冲击力下降比例Table 4 Comparison of percentage reduction of meshin impact force under various loads at design load of 2 339 N·m %

图10所示为设计载荷等于2 339 N·m，小轮转速等于3 000 r/min时，标准齿面、传统修形和改进修形啮入冲击力随载荷的变化。由图10可见：工作载荷范围内，载荷等于最常用载荷、最小载荷和最大载荷时的啮入冲击力都出现了较大幅度下降。与传统修形相比，改进修形显示出一定优越性，其啮入冲击力小于传统修形齿面啮入冲击力。

综合图8和图10可以发现，基于当量载荷为2 339 N·m 的齿面优化修形设计，保证了在最常用载荷1 948 N·m 下的齿轮副ALTE 和啮入冲击力大幅下降，同时兼顾了工作载荷范围内其他载荷下的齿轮副ALTE和啮入冲击力下降。

图10 设计载荷等于2 339 N·m时，3种齿面的啮入冲击力随载荷的变化Fig.10 Variation of mesh-in impact forces of three types of tooth surfaces with load at design load of 2 339 N·m

5 结论

1)在载荷谱中最常用载荷下，基于当量载荷的修形齿面的齿轮副承载传动误差幅值和啮入冲击力出现了较大幅度下降。其中，传统修形的承载传动误差幅值和啮入冲击力下降比例分别为38.6%和47.7%；改进修形的承载传动误差和啮入冲击力的下降比例分别为68.3%和56.5%。

2)基于当量载荷的齿面修形设计保证了载荷谱中几种常用载荷下的齿轮副承载传动误差和啮入冲击力下降。其中，传统修形可保证在几种常用载荷下使承载传动误差下降30%以上，使啮入冲击力下降40%以上；改进修形可保证在几种常用载荷下使承载传动误差下降40%以上，使啮入冲击力下降50%以上。

3)考虑了实测载荷谱工况下的优化修形齿面，在当量载荷、最常用载荷以及工作载荷范围内的大部分载荷下，改进修形都能够比传统修形更好地改进齿轮副啮合性能，可以更有效地减振降噪。