推杆针轮活齿传动齿形修形分析及优化
2020-07-28费宇张世友姚进谢超李华
费宇,张世友,姚进,谢超,李华
(1.四川大学 机械工程学院,四川 成都 610065; 2.四川省机械研究设计院,四川 成都 610063)
活齿传动是一种兼具结构紧凑、传动比范围广、承载能力大、传动效率高等优点的高性能多齿啮合传动[1]。传统的活齿传动中,中心轮齿形多为具有复杂曲线的内轮廓,其加工难度大,加工精度不易保证,限制了活齿传动的应用[2-4]。推杆针轮活齿传动以针轮(简单曲线)为中心轮,而将复杂齿形转移到活齿外轮廓上,与传统的活齿传动相比,其加工难度减小且加工精度易于保证,是一种在精密传动领域很有应用潜力的活齿传动形式[5-7]。
对于推杆针轮活齿传动这样的多齿啮合传动而言,理论上有一半的活齿与针轮啮合参与传动,并且参加传动的所有啮合副之间的间隙为零。但是,在多齿啮合传动中,加工和装配中不可避免地会产生误差。为防止发生齿形干涉,并使啮合副获得合适的齿侧间隙以及改善传动性能,多齿啮合传动的啮合副齿形必须进行修形[8]。近年来,国内外学者对多齿啮合传动的啮合副修形进行了大量研究。Meng等[9]提出一种修形后摆线针轮传动初始间隙的计算方法,得出“负等距+正移距”的组合修形可以获得最小的回转误差,Guan等[10]对这种组合修形产生的齿形进行了受力分析方法的研究,并进一步研究了这种组合修形对承载能力的影响。曲继方[11]针对具有复杂内齿廓中心轮的活齿传动,提出了“转角等距移距齿廓修形法”,李剑锋等[12]针对这一类型的活齿传动推导了中心轮的齿形通用方程式,并进行了初步的修形研究。李剑锋等[13-14]研究了凸轮激波滚动活齿传动的修形方法,提出顶根复合和转角-顶根复合修形2种方法,并对相应的修形齿形进行了受力分析。这些研究极大地推动了各种多齿啮合传动修形的应用和发展,但针对推杆针轮活齿传动修形的研究仍然较少。
本文对推杆针轮活齿传动的修形方法和修形量的优化进行了研究。通过分析使用等距、移距、转角等修形方法获得的活齿的修形齿形特点,提出“等距+移距”的组合修形适用于推杆针轮活齿传动的活齿修形。进一步,以回差大小作为修形齿形的评价标准,建立了修形齿形的回差数学模型,并分析了“等距+移距”组合修形不同组合方式的回差,得到针对推杆针轮活齿传动的齿形修形最佳组合方式。在此基础上,建立了以回差最小为目标函数的组合修形最佳修形量的优化模型,并结合实例验证了该优化方法的可行性。
1 推杆针轮活齿传动的结构和齿形修形方法
1.1 推杆针轮活齿传动的结构及工作原理
如图1所示,推杆针轮活齿传动由激波器H、活齿架G、针轮K和一组推杆活齿T构成,针轮K圆周上均布有一组圆柱形针齿P。活齿齿形是由针齿的运动包络形成的整条外轮廓曲线,每个活齿分别与激波器和针轮接触形成平面高副。若活齿数为zG,针轮上的针齿数为zK,则zK-zG=±1。

图1 推杆针轮活齿传动Fig.1 Push-rods oscillatory transmission with a needle gear
以激波器H作为输入件、活齿架G固定、针轮K作为输出件,当激波器以等角速度ωH绕机架中心O顺时针转动时,由于激波器具有偏心距,激波器将推动与其接触的推杆活齿沿活齿架上的活齿槽纵向移动,在它们的综合作用下,将推动针轮K绕机架O以等角速度ωK顺时针转动,实现了活齿传动的速度转换和功率传递。其传动比为:
(1)
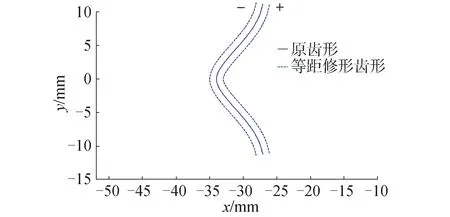
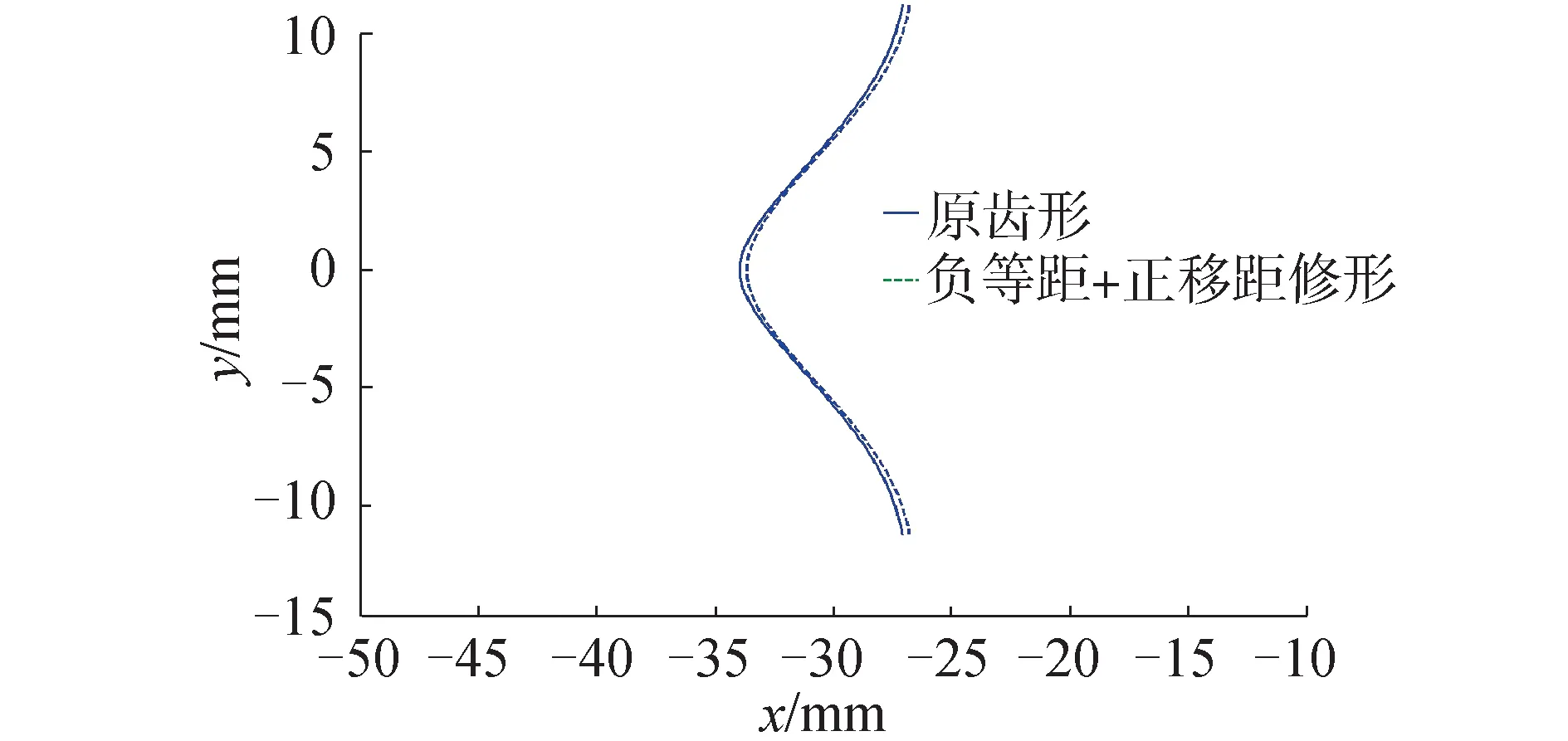
当zK>zG时,输入与输出转向相同;当zK 1.2.1 现有齿形修形方法及特点 齿形修形方法有很多[8],分为直接修形(等距修形、移距修形和转角修形)和间接修形。间接修形的方法在实际操作中由于具有加工装置互换性差的问题,一般不常使用。本文只对直接修形方法进行介绍。 1)等距修形(设等距修形量为Δrrp)。在活齿齿形加工装置上加工活齿时,刀具的半径(相当于啮合时的针齿半径)相对于标准的针齿半径rp有一个增量Δrrp,便可以加工得到如图2所示的原活齿齿形的等距修形曲线,规定刀具半径相对于标准针齿半径增大时修形量为正,反之为负。 图2 活齿齿形的等距修形Fig.2 Isometric modification of tooth profile 图2中实线为活齿的理论齿形曲线,虚线为等距修形过后的实际齿形曲线,其为活齿理论齿形的等距线。当等距修形量Δrrp为正时会在全齿廓上形成均匀的间隙,而当Δrrp为负时则会在全齿廓上形成均匀的过盈。 2)移距修形(假设移距修形量为Δrp)。在活齿齿形加工装置上加工活齿时,刀具的几何中心位置的实际向径相对于理论向径即针轮半径RK有一个增量Δrp,便可以加工得到如图3所示的原活齿齿形的移距修形曲线,规定刀具几何中心靠近针轮中心时修形量为正,反之为负。 图3 活齿齿形的移距修形Fig.3 Move modification of tooth profile 图3中实线为活齿的理论齿形曲线,虚线为移距修形过后的实际齿形曲线,其为活齿理论齿形的等向径曲线。当移距修形量Δrp为正时会在全齿廓上形成均匀的间隙,而当Δrp为负时则会在全齿廓上形成均匀的过盈。 3)转角修形。在活齿齿形加工装置上加工活齿理论齿形时,当理论齿形加工完成后,给加工完成的活齿工件附加一个转角,以微量磨削活齿理论齿形的一侧齿廓,得到如图4所示的原活齿齿形的转角修形曲线。 图4 活齿齿形的转角修形Fig.4 Angle modification of tooth profile 图4中转角修形曲线仅仅改变了活齿理论曲线在圆周方向上的位置,并使得活齿变薄,从而使共轭齿形在圆周方向上形成齿侧间隙,但在齿根和齿顶处不会形成间隙,因此转角修形在实际修形中不会单独使用。 1.2.2 推杆针轮活齿传动齿形修形方法的确定 由1.2.1小节所述可以看到转角修形不会单独使用,等距修形和移距修形方法单独使用时得到的齿形间隙或是过盈都是均匀的,这样的齿形除了能提供润滑间隙外,并不能达到调整各对共轭齿形间载荷分配和实现共轭齿形合理的啮合部位的目的。本文考虑“等距+移距”的组合修形方法。 在推杆针轮活齿传动的活齿修形中,考虑等距修形和移距修形的组合修形,是在保证共轭齿形齿顶和齿根径向间隙Δ=Δrp+Δrrp不变(本文取0.02 mm)的前提下,采用组合方法来获得比较理想的活齿齿形,即齿形中部的间隙较小,齿形两端的间隙略大,大部分的工作齿廓集中在齿形中部的活齿齿形。 “等距+移距”的组合修形可以得到以下4种组合:“正等距+正移距”、“负等距+负移距”、“正等距+负移距”以及“负等距+正移距”。由于“负等距+负移距”的组合修形产生的间隙为负间隙,装配和传动过程中会发生齿形干涉,因而无法采用。以“负等距+正移距”的组合修形便可以加工得到如图5所示的修形曲线。 图5 “负等距+正移距”组合修形Fig.5 Combination of “negative isometric modification+positive move modification” 图5中可以看到,修形形成的活齿齿形特征是活齿齿形中部到齿根和齿顶形成了逐渐增大的间隙,这样的齿形会在活齿传动中使得啮入的活齿承受的载荷量逐渐增加,啮出的活齿承受的载荷量逐渐释放,延缓了啮出卸载和啮入承载的过程,减轻了啮入啮出的冲击。“负等距+正移距”的组合修形利用合理的齿侧间隙不仅提高了活齿传动的传动性能,还解决了活齿齿顶和齿根部分参与到啮合时受力状态恶劣的难题。因而本文选择“等距+移距”的组合修形方法来对推杆针轮活齿传动的齿形进行修形。 活齿采用“等距+移距”组合修形后,变小的活齿在与针齿啮合时,相对于理论的标准位置,激波器需要转过一个角度,推动活齿沿活齿架上的径向导槽移动,才能和针齿接触,激波器相对于理论位置转过的这一角度叫做激波器相对转角。空载时,只有一个活齿与针轮上的针齿啮合,其他活齿与针轮上的针齿之间都存在一定的间隙,加载后,只有克服了间隙,其他的活齿才能参与到啮合中去,并且载荷越大,同时参与啮合的活齿数越多。同时,当输入轴反向转动时,齿侧间隙会导致输出轴上的输出滞后,即产生回差,并且间隙越大,回差越大。在机器人关节减速器中,回差是一个很重要的性能指标,本文以修形产生的回差大小为修形齿形优劣的评价标准。 以激波器H为输入构件,针齿为输出构件,固定活齿架G,建立图6所示的等距修形产生的激波器相对转角示意图。图中,O2为针齿中心,OH为激波器H中心,O为机架中心,也是针轮和激波器的旋转中心,以O为原点建立直角坐标系xOy。OOH=e为激波器的偏心距,φH为激波器相对于机架的转角,φK为针齿(针轮)相对于机架的转角,粗实线所示为未经过修形的活齿齿形,细实线所示为等距修形过后活齿的齿形。 图6 等距修形产生的激波器相对转角Fig.6 Relative angle of the surge wheel caused by isometric modification (2) 考虑△OO1OH和△OO'1O'H,由余弦定理可以得到: (3) 式中: 解得等距修形产生的激波器相对转角为: (4) 图7 移距修形产生的激波器相对转角Fig.7 Relative angle of the surge wheel caused by move modification Δrp·cosθ·cos (θ-φK) (5) 同理可得到移距修形产生的相对转角为: (6) 考虑“等距+移距”组合修形产生的激波器相对转角ΔφH,假设组合修形时激波器推动活齿沿x轴负方向移动的距离为Δx,则: Δx=Δx1+Δx2 (7) 则“等距+移距”组合修形产生的激波器相对转角为: (8) 当以针轮作为输出时,组合修形后产生的针轮相对转角可以表示为: ΔφK=ΔφH/i (9) 式中i为推杆针轮活齿传动的传动比。 由于“等距+移距”组合修形后的齿形相对于活齿的理论位置左右对称,且多齿啮合时最小齿隙的地方总是最先接触,组合修形导致的回差γ可以用针轮相对转角最小值的2倍来表示,即: γ=2ΔφK min (10) 1.2节的研究表明,“等距+移距”的组合修形只有3种组合方式是适合活齿修形使用的,即“正等距+正移距”,“正等距+负移距”和“负等距+正移距”。本文以实例来分析这3种组合修形方式的回差,从而确定修形的最佳组合方式。确定一组推杆针轮活齿传动的结构参数,如表1所示。 表1 推杆针轮活齿传动结构参数Table 1 Structural parameters of the push-rods oscillatory transmission with a needle gear 在保证修形后活齿齿顶和齿根形成0.02 mm径向间隙的条件下,参照式(9)和式(10)来研究。由于修形后的齿形是左右对称的,因而下面只研究修形活齿一半的齿形,即研究在激波器旋转0°~180°的范围内针轮的相对转角。 图8为采用“等距+移距”组合修形后产生的针轮相对转角。初步设计“负等距+正移距”组合修形的修形量为Δrrp=-0.01 mm、Δrp=0.03 mm,“正等距+负移距”组合修形的修形量为Δrrp=0.03 mm、Δrp=-0.01 mm,“正等距+正移距”组合修形的修形量为Δrrp=0.01 mm、Δrp=0.01 mm。 图8 组合修形产生的针轮相对转角Fig.8 Relative angle of the needle gear caused by combination modification 由图8可以看到,采用“负等距+正移距”的组合修形方式在齿形工作区段产生的针轮相对转角,无论是最小相对转角还是平均相对转角,在3种组合修形方式中都是最小的,因而对推杆针轮活齿传动而言,“负等距+正移距”组合修形方式更优,当推杆针轮活齿传动的结构参数改变时,结果与该实例一致。在本实例中,“负等距+正移距”产生的最小针轮相对转角ΔφK min=0.01°,将其代入式(10)可以得到实例中产生的回差γ=0.02°。 要满足精密传动的要求,修行产生的回差要尽可能小。通过优化设计方法可以求得“负等距+正移距”组合修形的最佳的修形量,使得在满足一定条件的情况下,修形产生的回差最小。 本文在满足齿顶和齿根径向间隙为0.02 mm,即Δrrp+Δrp=0.02的条件下,以针轮相对转角ΔφK最小为目标函数,以φH、Δrrp、Δrp为自变量进行优化求解。由式(8)和式(9)得目标函数为: (11) 结合式(2)、(5)、(7)进行分析。 采用“负等距+正移距”组合修形,所以有Δrrp≤0,Δrp≥0;修形后的齿形是左右对称的,所以可以限制激波器转角φH的范围为0°~180°;为了减小优化分析的范围,限定Δrrp≥-0.1,Δrp≤0.1。其具体的约束条件如下: (12) 保持结构参数不变,利用Matlab的多维非线性优化求解函数fconmin可以求得采用“负等距+正移距”组合修形时使得针轮相对转角ΔφK最小的激波器转角以及最佳修形量分别为φH=91.67°,Δrrp=-0.061 mm,Δrp=0.081 mm。此时修形产生的针轮相对转角如图9所示。 和图8相比,图9针轮平均相对转角和最小相对转角都有所减小,其中最小相对转角ΔφK min=0.003°,相应地,修形导致的回差γ=0.006°,满足机器人关节减速器的传动精度要求。 图9 优化修形产生的针轮相对转角Fig.9 Relative angle of the needle gear caused by optimized modification 优化修形后得到的修形齿形如图10所示。可以看到优化后的修形齿形的齿形中部的间隙较小,从齿形中部到齿根和齿顶的间隙则逐渐增大,所以大部分的工作齿廓集中在齿形中部(15°~165°)。 图10 组合修形优化齿形Fig.10 The optimized tooth profile with combination modification 1)“等距+移距”的组合修形利用合理的齿侧间隙不仅提高了活齿传动的传动性能,还解决了活齿齿顶和齿根部分参与到啮合时受力状态恶劣的难题,适合推杆针轮活齿传动的齿形修形。 2)分析了“等距+移距”组合修形不同组合方式的回差,结果表明,“负等距+正移距”的组合修形方式较其他两种组合方式,修形产生的回差最小,是最适合推杆针轮活齿修形的组合方式。 3)实例中最佳修形量的优化结果表明,采用等距修形量Δrrp=-0.061 mm和移距修形量Δrp=0.081 mm的组合修形,在激波器转角为φH=91.67°时产生的回差仅为0.006°,满足机器人关节减速器的精度要求,证明了优化方法的可行性。1.2 推杆针轮活齿传动齿形修形方法


2 活齿齿形修形的回差数学建模与最佳组合方式
2.1 等距修形产生的相对转角


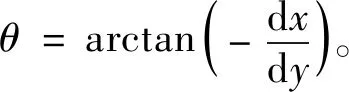
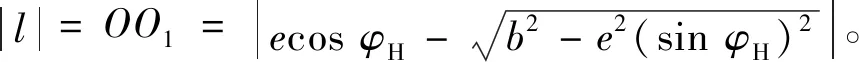
2.2 移距修形产生的相对转角
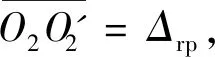


2.3 组合修形产生的回差
2.4 “等距+移距”组合修形的最佳组合方式

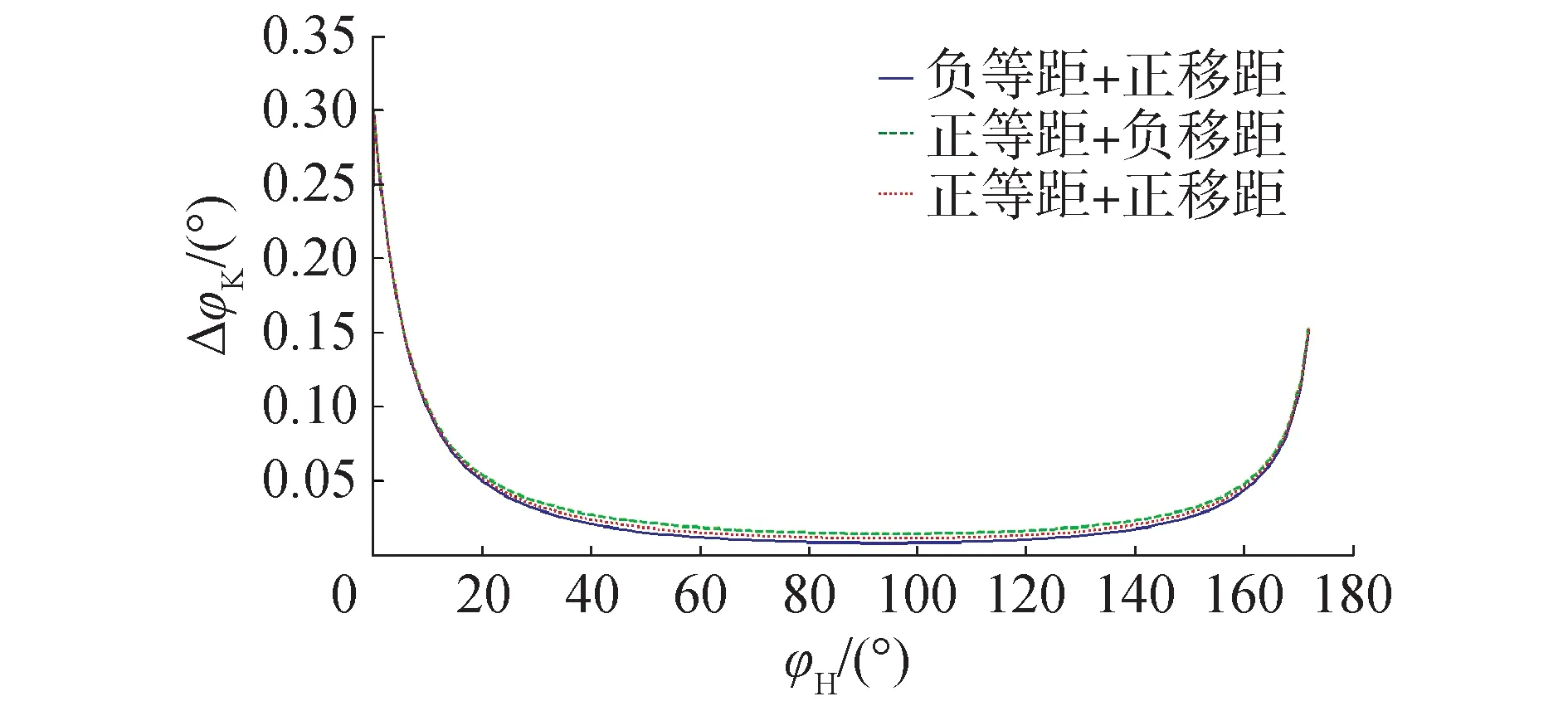
3 推杆针轮活齿传动的活齿齿形修形量优化
3.1 优化模型
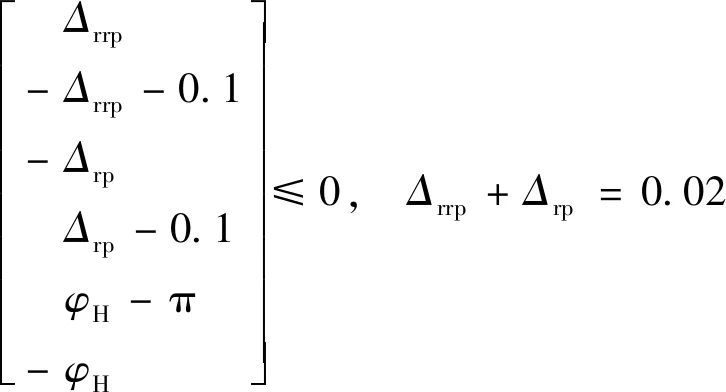
3.2 结果与分析
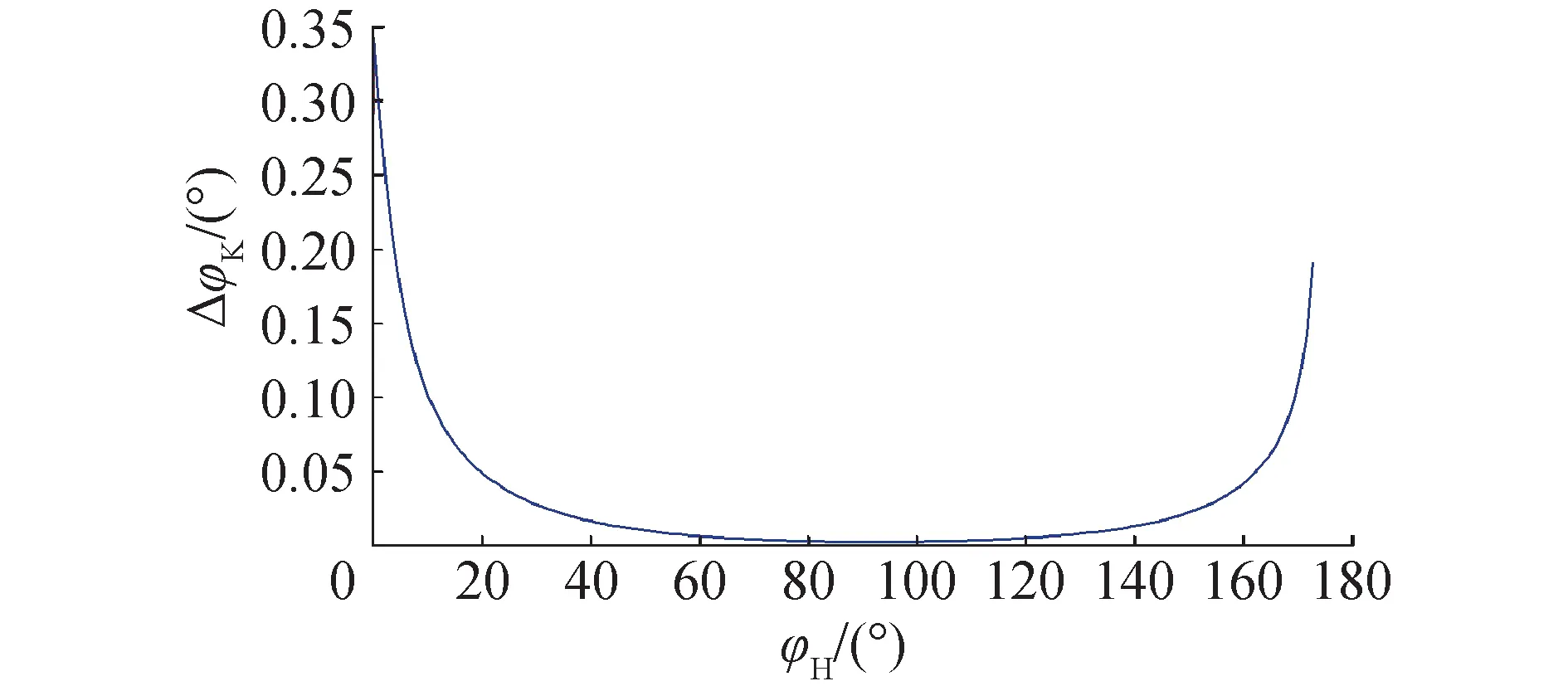

4 结论
