Linex损失下两种信用评分模型的比较

刘延喜

(长春大学 理学院，长春 130022)

0 引言

目前，有很多方法可以用于信用评分，如K近邻法、Bayes决策模型、决策树、支持向量机、投影寻踪学习网络和神经网络等方法［1－5］。信用评分中高估和低估客户信用产生的损失不一样，有学者把非对称损失引入到信用评分模型中，经实验证明确实有效。本文介绍Linex损失下投影寻踪学习网络和BP神经网络这两种同类的模型，并对其进行了实验比较。

1 算法

1.1 Linex 损失［6］

定义1 设用d估计y时所引起的损失为

该损失函数称做Linex损失。

1.2 基于Linex损失的BP神经网络改进算法

考虑一个三层前馈神经网络，其输入层、隐层和输出层的神经元个数分别为 p，q和1，记 w0=(w01，w02，…，w0q)T∈Rq为隐层与输出层之间的权向量，wi=(wi1，wi2，…，wip)T∈Rp为输入层与隐层第i个节点之间的连接权向量，其中 i=1，2，…，q。记。隐层、输出层的激活函数为 g:R→ R。对任意x=(x1，x2，…，xq)∈Rq，记 G(x)=(g(x1)，g(x2)，…，g(xq))T:Rq→Rq。对输入样本ξ∈RP，隐层的输出为G(Vξ)，网络输出层的输出为ζ=g(w0·G(Vξ))。给定一个ξj为输入样本，Oj为目标输出的训练样本集{ξj，Oj}Jj=1，Linex损失的误差函数为

其中gj(t)=exp(α(Oj－g(t))－α(Oj－g(t))－1。

E(W)的梯度为

从某一初始权值W0开始，批处理算法的权值更新规则如下:

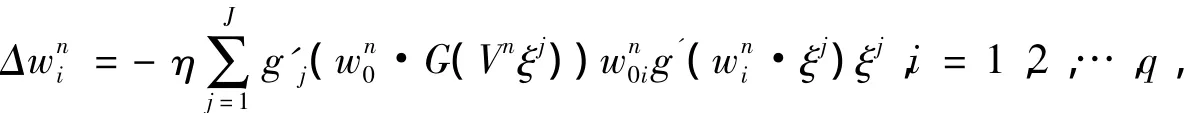
这里学习率η＞0为一个常数。

1.3 Linex 损失下投影寻踪学习网络［7－9］

设X=(x1，x2…xp)T为投影寻踪学习网络的输入，y1，y2，…，yq为期望输出是输入层和隐层的连接权向量，k=1，2，…，m，gk(·)是隐层的激活函数，k=1，2，…，m，βik为隐层第k格激活函数和输出层第i个元yi的连接权为网络的实际输出，输入和输出满足如下关系:

投影寻踪学习网络的三类参数估计由最小化学习准则求得:

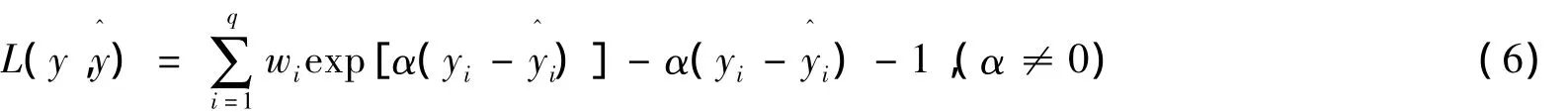
其中wi，1≤i≤q是学习速率。

投影寻踪学习网络采取交替优化方法来确定输入层权值、隐层激活函数和输出层权值这三类参数，做法是以隐层激活函数gk(·)为主，将与gk(·)有关的参数设为一组，全体参数分成m组。除其中一组以外，都给定初值，然后对留下的一组求最优，求得结果后，把这一组参数作初值，另选一组参数做优化。多次重复直道误差精度满足要求为止。

1)权值 βik的估计可得到参数βik的最小二乘估计，βik的估计可直接求得

2)隐层激活函数gk(·)的估计)。固定投影方向和输出权值βik，可以求得

还可以用Hermit或其它标准正交多项式逼近隐层激活函数。

3)权值αk的估计。通常采用Gauss-Newton等无约束最优化方法求解，在无法求导数，可采用差分拟牛顿等。

2 实验及结果

UCI中汉堡大学Hans Hofmann教授提供了德国一家银行的1000个观测数，数据集含7个数值型、13个分类型和一个标志型信用字段，共21个字段。研究者假设将信用差的客户评为信用一流客户时的损失为5，而将信用一流客户评为不良客户时损失为1，这是合理的假设。使用对称性损失函数构造的投影寻踪学习网络等算法进行信用评分，忽视了上述损失的不同，使用本文讨论的Linex损失投影寻踪学习网络LPPLN和BP神经网络LBP，对客户进行信用评分更合适。

分别采用3层LPPLN和LBP进行信用评分，输入节点数为20，输出节点数为1，隐层节点选取3和4个两种。将1000个样本随机等分为4个互不相交的子集，训练时使用其中一部分为测试集，其它子集作为训练集。分别进行4次实验，相对误差阈值设为0.005，分类截取阈值取0.5。采用Linex损失函数的的重点是找出不良信用客户，将不良信用客户估计为信用好的客户称为第Ⅰ类错误，实验结果见表1。

表1 信用评分实验结果

3 结语

实验结果表明，3个隐层节点和4个隐层节点的网络，无论第Ⅰ类错误率还是总错误率，基于Linex损失下改进的投影寻踪学习网络优于BP神经网络。投影寻踪学习网络和BP神经网络成长于统计学和人工智能两个不同领域，但都基于本质上相同的模型。或许因为上世纪八十年代投影寻踪学习网络出现的时候，它对计算的要求超出了当时计算机的能力，它没有广泛的应用于统计学领域，其中很多问题值得探讨。

［1］Thomas L C.A survey of credit and behavioural scoring:Forecasting financial risk of lending to consumers［J］.International Journal of Forecasting，2000，16(2):149－172.

［2］West D.Neural network credit scoring models［J］.Computers and Operations Research，2000，27(11－12):1131－1152.

［3］Hand D J，Henley W E.Statistical classification methods in consumer credit scoring:A review［J］.Journal of the Royal Statistical Society，Series A(Statistics in Society)，1997:160(3):523－541.

［4］Baesens B，Van Gestel T，Viaene S，et al.Benchmarking state-of-the-art classification algorithms for credit scoring［J］.Journal of the Operational Research Society，2003，54(6):627－635.

［5］Ligang Zhou，Kin Keung Lai and Lean Yu.redit scoring using support vector machines with direct search for parameters selection［J］Soft Computing-A Fusion of Foundations，Methodologies and Applications，2009，13(2):149－155

［6］Zellner A.Bayesian Estimation and Prediction Using Asymmetric Loss Function［J］.JAmer Statist Assoc，1986，81(1):446－451.

［7］Jones L.K.A Simple Lemma on Greedy Approximation in Hilbert Space and Convergence Rates for Projection Pursuit Regression and Neural Network Training［J］.The Annals of Statistics，1992，20(1):608－613.

［8］严勇，李清泉，等.投影寻踪学习网络的遥感影像分类［J］.武汉大学学报:信息科学版，2007，32(10):876－879.

［9］李颖，陈兴林.投影寻踪网络用于光纤陀螺噪声消除的研究［J］.光子学报，2009，38(1):94－98.