复杂轮胎钢帘线双尺度结构分析

危银涛 罗亦文 缪一鸣 柴德龙 冯希金

1.清华大学汽车安全与节能国家重点实验室，北京，100084

2.贝卡尔特钢丝帘线亚洲技术中心，江阴，214434

3.杭州朝阳橡胶有限公司，杭州，310008

0 引言

有限元方法在轮胎研究中的应用始于20世纪70年代［1－7］。目前已发展到用有限元方法分析轮胎 滚 动 损 失［8－10］、断 裂［11－15］和 轮 胎 动 力 学［16－23］等方面。为了研究子午线轮胎钢丝帘线的受力与变形规律，在建立轮胎整体模型的过程中，采用rebar（加强筋）单元［24］模拟钢帘线。rebar单元本质上是一维杆单元，只能承受轴向拉压变形，而实际钢帘线是由若干单丝捻合成股后，再由股捻合而成的三维空间结构，在轮胎结构中除受拉外，还有弯曲变形，而现有的整体模型不足以全面细致地揭示帘线的力学性能。

笔者基于已有的轮胎整体建模理论，提出一种研究帘线内部应力和应变的局部分层建模新方法。在局部尺度建模过程中，将帘线的设计变量（帘线捻角、捻距、帘线中心半径）作为建模输入参数建立含单丝信息的有限元模型，将从整体模型中获得的钢丝帘线典型变形和应力作为载荷边界条件。

1 全钢载重子午线轮胎的整体建模

基于rebar技术［24］，在充气压力为840kPa、负荷为3675kg的条件下，对某全钢载重子午线轮胎进行整体建模。图1a显示的是轮胎整体模型中的材料分布状况；图1b是钢丝帘线的分布示意图。

1.1 帘线张力

对于载重子午线轮胎，钢丝帘线是承载的主要部件。钢丝的分布不仅影响自身受力，还影响胶料的剪应力和剪应变，最终影响到轮胎的耐磨性、刚性、生热性和滚动阻力等。充气压力条件下，第二带束层帘线的张力大小沿帘线呈抛物线形状，帘线中心位置（冠部）为抛物线顶点，此处的张力最大，为372N；帘线两端张力最小，为4N。对于胎体帘线，中间（冠部）区域的受力要小于两胎侧区域的受力，从上胎侧到下胎侧，帘线受力几乎不变，胎圈部位帘线张力有所增加，但到达峰值之后帘线张力开始下降，到帘线端点张力下降到零。

图2 第二带束层帘线受力分布

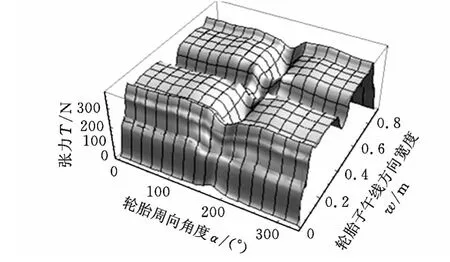
图3 胎体帘线受力分布

在充气载荷和垂直载荷的共同作用下，轮胎帘线的受力状况不同于纯充气状态的受力状况，主要表现为对接地区域的影响。图2、图3分别为第二带束层帘线与胎体帘线的受力分布三维图，底面上两个互相垂直的坐标轴分别表示沿子午方向的宽度（沿胎体帘线长度）和轮胎的周向角度（轮胎最高点为0°，最低点为180°），纵轴表示轮胎帘线张力。从图2可知，第二层带束层帘线为主要承载层，承受大部分的充气压力和外部负荷，带束帘线受力具有3个特点：①帘线的受力与圆周的胎面中心线呈反对称；②在接触区域，帘线受力在冠部区域减小而在带束层的末端增大；③帘线受力的最大值转移到胎肩区域的带束末端，最小值转移到冠部中心区域，即接触使带束帘线受力在冠部区域松弛，在胎肩区域增加。从图3可知，胎体帘线应力分布的一个重要特点是：在轮胎与地面的接触区域，帘线应力有所减小；在接触区域以外，胎体帘线应力基本不变。

1.2 胎体弯曲应力

如果胎体曲率已知，那么帘线的应力［25－27］：

式中，r为单丝半径，r＝0.11mm；E为帘线材料的弹性模量，E≈200MPa；Δκ为胎体曲率。

式（1）表明帘线中的单丝均独立弯曲，且曲率相同。因此，一根单丝的曲率可以从的胎体整体变形中获得

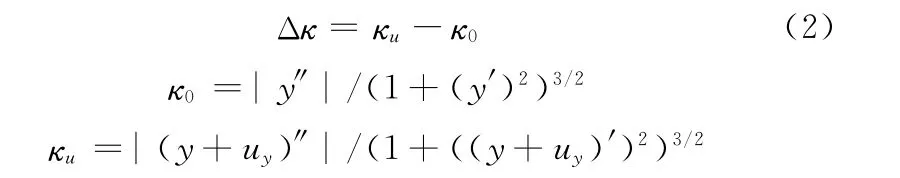
式中，κu为胎体变形后的曲率；κ0为原始曲率；uy为y方向的位移，由整体分析得到。

变形前后y的二阶偏导数可用差分求得

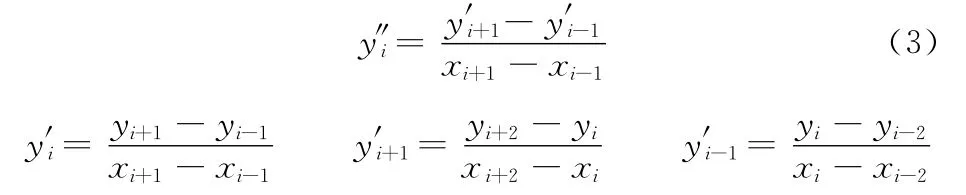
由式（2）、式（3）分别可以得到弯曲应力和弯曲曲率，为进一步分析帘线的局部变形提供了载荷边界条件。帘线的局部变形包括丝与丝之间接触应力需要更精细的局部模型。

2 复杂多股钢丝帘线的有限元建模

为了全面细致地揭示帘线的变形机制，创建帘线局部分层有限元模型。在局部建模中采用的胎体弯曲曲率为25m－1（或曲率半径为40mm），同时，对帘线施加从50～300N的张力。

2.1 复杂钢帘线双螺旋结构的几何描述

为了给复杂的多股钢丝帘线划分网格，首先要精确地描述其几何变形特征。图4所示是一种3＋9＋15×0.22＋0.15的三层钢丝帘线结构，其内层为3根单丝，中间层为9根单丝，外层为15根单丝，单丝直径均为0.22mm，外绕丝直径为0.15mm。图5所示帘线为一种双螺旋结构钢帘线，帘线由3股钢丝螺旋捻合组成，每股又由4根单丝螺旋捻合组成，单丝直径均为0.22mm，其表述形式为3×4×0.22。钢丝帘线指定层的单螺旋中心线均可由以下参数方程描述：

式中，Rs为单螺旋中心线的半径；αs为捻角；θs为旋转角；θs0为初相角。

对于三层钢丝帘线，单一螺旋线结构足以描述其几何形状。对于双螺旋结构帘线，以局部坐标轴为基础的数学方程能更方便描述钢丝的几何特性。对于图6所示的螺旋结构，定义局部Frenet－Serret轴t、n、b（分别为沿着螺旋线的切线、法线和副法线的单位向量）［28-29］：

图4 三层结构钢丝帘线

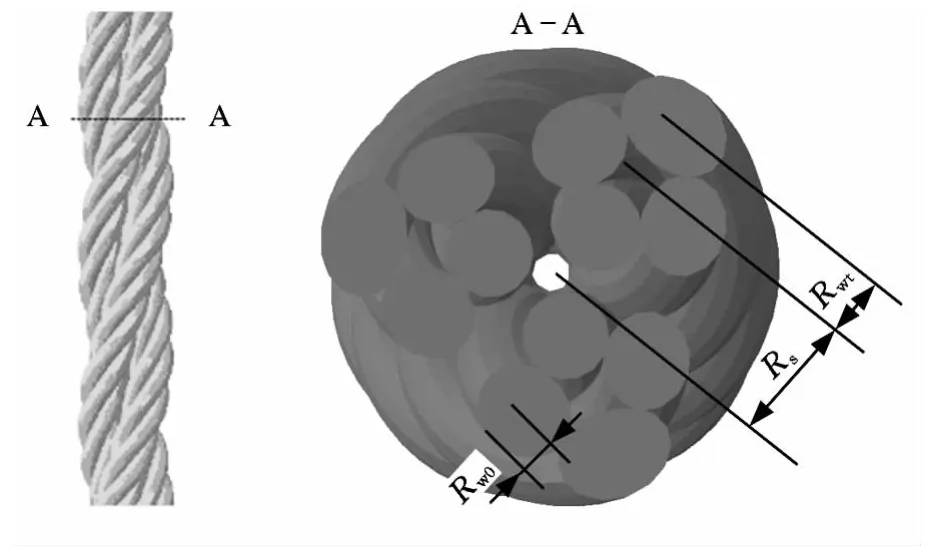
图5 双螺旋结构多股钢丝帘线

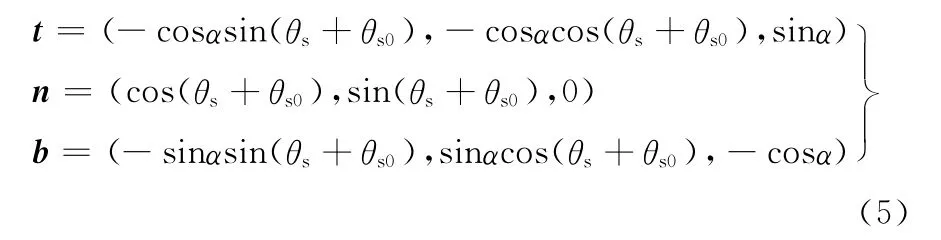
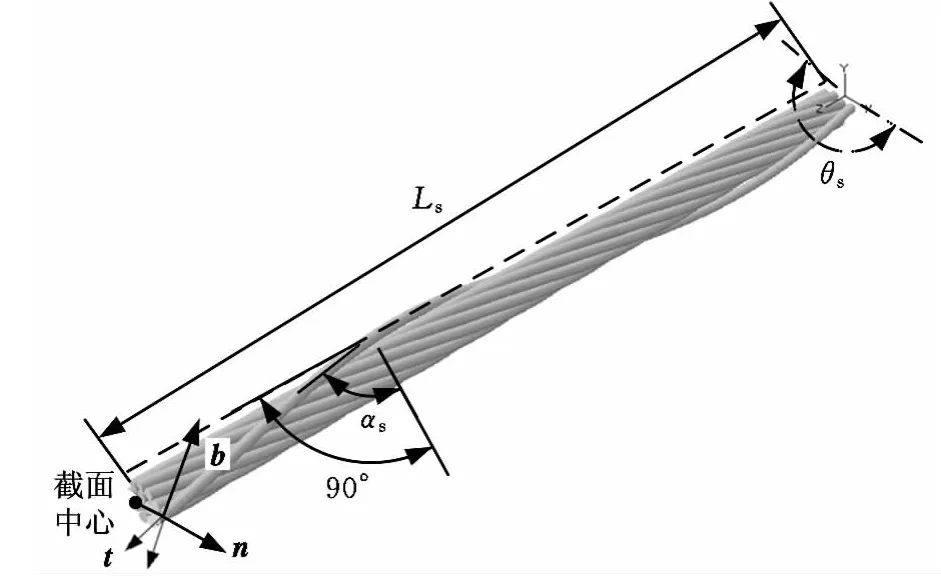
图6 螺旋结构的几何特性描述

整体坐标系到局部Frenet－Serret坐标系的坐标转换矩阵可以根据帘线参数写为

则局部Frenet－Serret坐标系到整体坐标系的坐标转换矩阵对a求逆即可：

局部坐标系中，矢量r转化为整体坐标系：

不同层旋转角度关系如下：

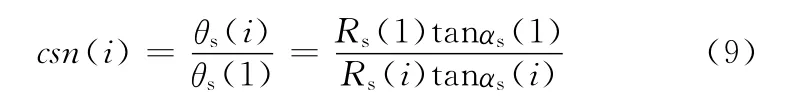
式中，αs（i）为第i层的捻角；θs（i）为第i层的旋转角度；Rs（i）为第i层的单螺旋曲线的中心线半径。

双螺旋中，股的旋转角度和单丝旋转角度之间的关系为

式中，θw（i，j）为第i层的第j子层的旋转角度；αwt（i，j）为第i层的第j子层的捻角。

基于上述双螺旋帘线结构的数学描述，设计一个递归程序来获得复杂帘线的几何形状，其算法如下：

（1）每个股层中股的初相角由下式决定：

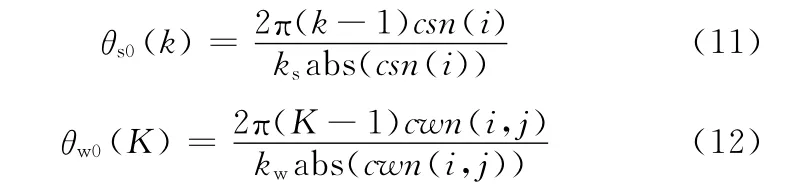
式中，θs0（k）为第i层第k（k＝1，2，…，ks）根单丝的初相角；ks是第i层中的单丝总数；θw0（K）为在第i层的第j子层的第K（K＝1，2，…，kw）线的初相角；kw为在第i层的第j子层的钢丝总数。

（2）层和子层的旋转角度增量。第k层股的增量旋转角度为

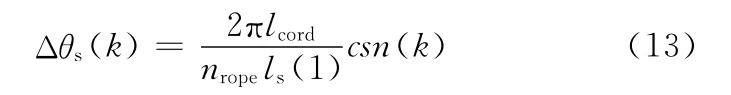
式中，ls（1）为第1层股的长度；lcord为模型中帘线的长度；nrope为沿帘线中心线方向的节点数量。

单丝旋转角度为

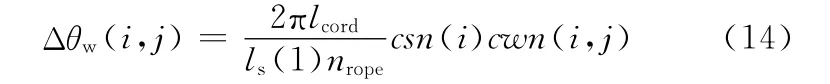
式中，Δθw（i，j）为第i层的第j子层的增量旋转角度。

（3）单螺旋中心线上点的坐标可以用式（4）进行计算。

（4）单螺旋表面点的计算方法如下：

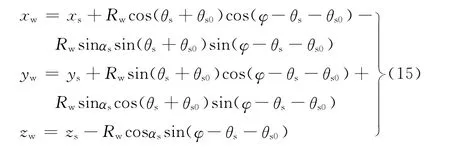
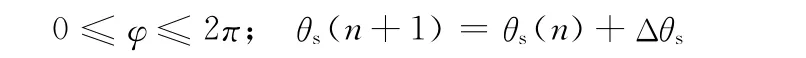
为了推导式（15），首先将从单螺旋中心线到表面点矢量写成

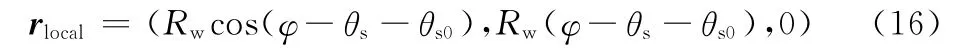
将式（8）的坐标转换关系应用到式（16）就可以推导出式（15），得到单螺旋表面点坐标的解析描述。

（5）对双螺旋结构，坐标变换公式必须使用两次。

双螺旋结构的中心线可描述为

式中，Rwt为股中心到单丝中心的距离。

双螺旋结构的表面节点的计算方法如下：

重复上述步骤（1）～步骤（5）（式（11）～式（19）），可以得到任意复杂的多股帘线精确数学描述。

2.2 有限元网格划分

基于上述工作，笔者开发了专用程序Cablemesh来建立多股钢帘线有限元模型，输入参数包括帘线设计变量（捻距、捻角、螺旋中心线半径）和网格参数（帘线模型长度，沿轴向、径向和圆周方向的网格密度）。建模过程中，所有的单丝表面将产生接触。图7所示为典型的双螺旋钢帘线有限元模型。

图7 双螺旋钢丝帘线有限元模型

3 帘线拉力仿真

研究了上述两种型号钢帘线（帘线长度均为20mm）。仿真中，钢丝本体材料采用弹塑性本构模型，材料模型参数用拉伸试验方法得到，试验在Zwick材料试验机上进行。为正确仿真单丝的受力，有限元模型的单元必须保证精确，一个基本的准则是在单丝的径向至少划分3个单元，而在单丝的周向至少划分20个单元。根据这一准则三层钢帘线模型被划分为168 000个单元，而双螺旋模型被划分为72 000个单元，模型考虑了所有可能接触的单丝对，计算在32核CPU并行机上进行。

图8、图9分别给出了两种帘线的测试与有限元仿真应力－应变曲线。曲线表明：有限元仿真和试验数据吻合得很好；双螺旋帘线是一种高伸长帘线，仿真和试验都可以清楚地观察到在拉伸过程中分别产生结构变形、弹性变形和弹塑性变形（图8）。三层钢帘线是一种高强度钢帘线，其结构变形阶段不明显（图9）。产生差异的主要原因在于两种帘线的结构设计不同，相比于三层钢帘线，双螺旋帘线有相对较小的捻距和捻角，在拉伸过程中要经历较大的结构变形后，才能在丝与丝之间形成稳定的接触平衡；两种型号帘线的基本特征都能够用有限元来模拟，从而证明了模型的有效性和合理性。

图8 双螺旋帘线的拉力－应变曲线

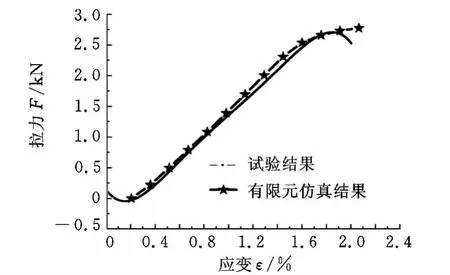
图9 三层帘线的拉力－应变曲线

4 拉伸与弯曲组合分析

对长为20mm的三层钢丝帘线进行拉弯组合变形仿真。在帘线末端截面中心施加Δθ转角和张力，产生拉伸－弯曲组合变形，使帘线紧贴在半径为40mm滚筒上，张力大小分别为50、100、200、300N。

旋转角度Δθ为圆筒上变形帘线的角度跨度，可表示为

式中，L为帘线长度，L＝20mm；ε为等效拉伸应变；r为圆筒半径，r＝40mm；Rs为钢帘线半径，Rs＝0.11mm。

假设单丝独立弯曲，帘线中钢丝的应力水平为［25-27］

式中，Ew为钢丝的弹性模量；Rw为单丝半径。

根据式（21），计算得出三层中单丝的弯曲应力水平为523MPa；采用有限元仿真，三层模型中单丝最大拉伸应力为470MPa，最大压缩应力为484MPa。图10给出了离加载末端10mm处截面上的Von Mises应力分布，从中可以得出以下结论：①单丝在拉伸与弯曲组合载荷作用下均独立弯曲。②弯曲中性轴的几何位置取决于帘线所在层的位置和拉力水平。最内层单丝中性轴偏移到压缩区，最外层单丝中性轴几乎仍在几何中轴。③单丝之间的接触显着地改变了局部的应力状态，单丝之间接触面的增加极大地提高了单丝局部压力。

5 轮胎钢帘线应变的测量

5.1 应变计系统设计

考虑到 1／4桥式传感器法［30－31］与钢条法［31］均有不足，笔者提出一种测量全钢载重子午线轮胎帘线受力的新方法——焊接法。如图11所示，该方法在帘线特定的位置上焊锡，再将焊料磨成方形柱状，然后在方柱的表面粘合应变计。帘线直径约为1.7mm，轮胎制造过程中的最高温度约为185℃，故选用QFLK－1－11－1LE应变计及60通道静态应变仪。

5.2 拉伸曲线标定

钢帘线埋胶硫化后的试样如图12所示。比较用Zwick试验机测量埋胶硫化试样得到的拉伸力－应变曲线和从应变计得到的拉伸力－应变曲线，可以发现二者之间有一定的差别（图13）。所以在应用应变计的数据之前，要对其进行标定，即用Zwick测量数据对应变计测量得到的曲线特性进行标定。

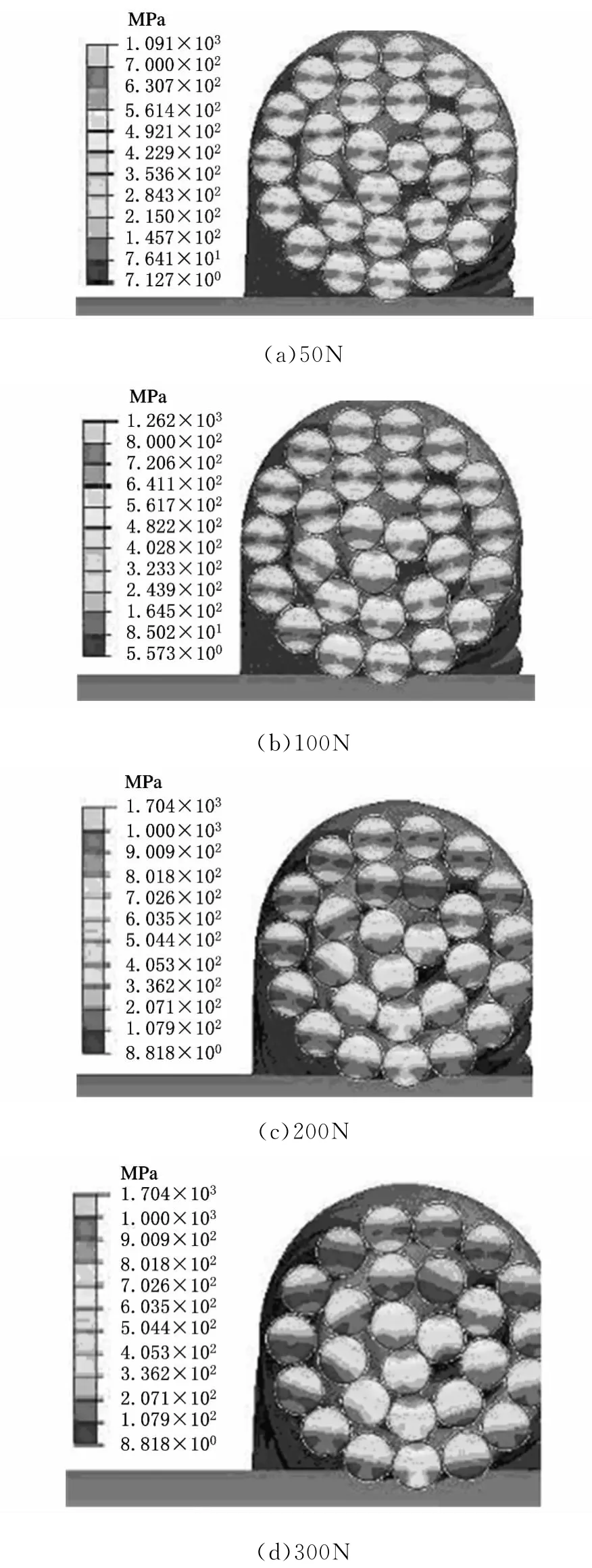
图10 不同拉力下三层帘线离末端10mm处截面的Mises应力分布

图11 帘线应变测量实验中试样的焊接方法

图12 钢帘线埋胶硫化后的试样

5.3 样胎制备与帘线受力测量

用粘贴好应变片的帘线替换带束层、胎体层等骨架材料中选定位置的帘线，在成形鼓上完成轮胎制造并硫化成形，得到测试用样胎。测量轮胎内帘线的受力时，充气压力为840kPa，将埋于轮胎浅表层的导线引出，与试验台、应变仪一起搭建帘线受力测量平台，见图14。

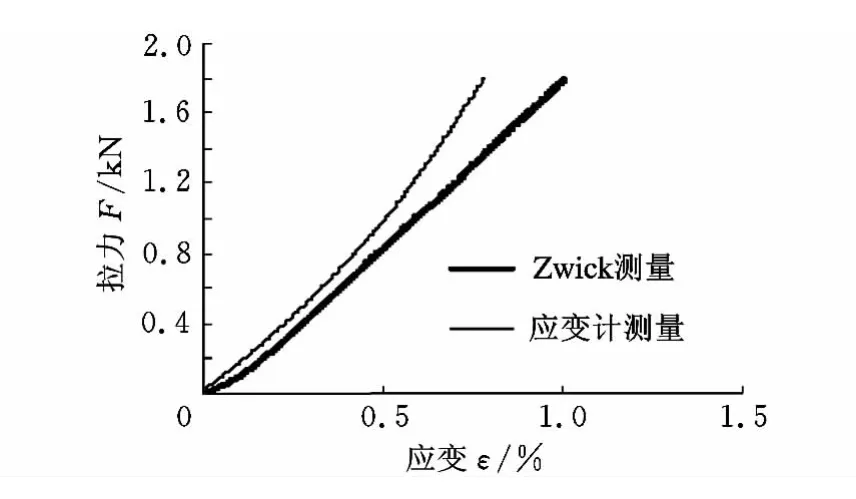
图13 埋胶硫化后试样的拉力－应变曲线

图14 TBR帘线应变的测量平台

5.4 测量结果与讨论

如图15所示，帘线上的字母a～k表示在该点的应变计能够测到实验数据，有少量的应变计无法测到试验数据。图16显示的是已测的试验数据和有限元分析结果，可以发现试验和仿真较一致。

图15 有效应变计的位置

图16 充气状态下轮胎帘线受力试验与有限元仿真的结果

6 结语

结合已有的整体尺度模型，笔者提出了一种全面细致分析载重子午轮胎钢丝帘线变形和应力的双尺度建模方法。开发的局部尺度模型须以整体尺度模型得到的帘线典型弯曲变形和拉力分布为输入。研究结果表明：对于双螺旋（高伸长率）帘线，在拉伸仿真和实验中能清楚地观察到结构变形、弹性变形及弹塑性变形阶段，而对三层（高强度）帘线，在拉伸仿真和实验中发现其结构变形阶段不明显、弹性阶段的刚度更大、塑性变形比较小；拉弯组合仿真中，单丝均独立弯曲，最内层单丝中性轴偏移到压缩区，最外层单丝中性轴几乎仍在几何中轴，单丝之间接触面的增大极大地提高了单丝局部压力；与试验结果的比较验证了有限元分析方法的正确性。

［1］Zorowski C F.Mathematical Prediction of Dynamic Tire Behavior［J］.Tire Science and Technology，1973，1（1）：99－117.

［2］De Eskinazi J，Soedel W，Yang T Y.Contact of an Inflated Toroidal Membrane with a Flat Surface as an Approach to the Tire Deflection Problem［J］.Tire Science and Technology，1975，3（1）：43－61.

［3］Kaga H，Okamoto K，Tozawa Y.Stress Analysis of a Tire under Vertical Load by a Finite Element Method［J］.Tire Science and Technology，1977，5（2）：102－118.

［4］De Eskinazi J，Yang T Y，Soedel W.Displacements and Stresses Resulting from Contact of a Steel Belted Radial Tire with a Flat Surface［J］.Tire Science and Technology，1978，6（1）：48－70.

［5］Watanabe Y.Finite Element Model for Analysis of Deformations of Bias－ply Motorcycle Tires Subject to Inflation Pressure［J］.Vehicle System Dynamics，1984，13（3）：113－128.

［6］Kung L E，Soedel W，Yang T Y.Free Vibration of a Pneumatic Tire－wheel Unit Using a Ring on an Elastic Foundation and a Finite Element Model［J］.Journal of Sound and Vibration，1986，107（2）：181－194.

［7］Gall R，Tabaddor F，Robbins D，et al.Some Notes on the Finite Element Analysis of Tires［J］.Tire Science and Technology，1995，23（3）：175－188.

［8］Tan H F，Du X W，Wei Y T，et al.Mechanical Properties of Cord－rubber Composites and Tire Finite Element Analysis［J］.Vehicle System Dynamics，2004，40（S）：161－174.

［9］Shida Z，Koishi M，Kogure T，et al.Rolling Resistance Simulation of Tires Using Static Finite Element Analysis［J］.Tire Science and Technology，1999，27（2）：84－105.

［10］Wei Y T，Nasdala L，Rothert H.Analysis of Tire Rolling Contact Response by REF Model［J］.Tire Science and Technology，2004，32（4）：214－235.

［11］HanY H，Becker E B，Fahrenthold E P，et al.Fatigue Life Prediction for Cord－rubber Composite Tires Using a Global－lcal Finite Element Method［J］.Tire Science and Technology，2004，32（1）：23－40.

［12］Wei Y T，Tian Z H，Du X W.Finite Element Model for The Rolling Loss Prediction and Fracture A－nalysis of Radial Tires［J］.Tire Science and Technology，1999，27（4）：250－276.

［13］Pek O S，Becker E B.Finite Element Method for the Study of Belt Edge Delaminations in Truck Tires［J］.Rubber Chemistry and Technology，2005，78（4）：557－571.

［14］Feng X，Yan X，Wei Y，et al.Analysis of Extension Propagation Process of Interface Crack between Belts of a Radial Tire Using a Finite Element Method［J］.Applied Mathematical Modeling，2004，28（2）：145－162.

［15］Feng X，Yan X，Wei Y，et al.Nonlinear Finite Element Modeling of Delamination Crack Growth Process between Belts of a Radial Tire［J］.Journal of Reinforced Plastics and Composites，2004，23（4）：373－388.

［16］ZhangY，Hazard C.Effects of Tire Properties and Their Interaction with the Ground and Suspension on Vehicle Dynamic Behavior－a Finite Element Approach［J］.Tire Science and Technology，1999，27（4）：227－249.

［17］Rao K，Kumar R，Bohara P.Transient Finite Element Analysis of Tire Dynamic Behavior［J］.Tire Science and Technology，1998，31（2）：104－127.

［18］Kerchman V.Tire－suspension－chassis Dynamics in Rolling over Obstacles for Ride and Harshness Analysis［J］.Tire Science and Technology，2008，36（3）：158－191.

［19］Brinkmeier M，Nackenhorst U.An Approach for Large－scale Gyroscopic Eigenvalue Problems with Application to High－frequency Response of Rolling Tires［J］.Computational Mechanics，2008，41（4）：503－515.

［20］Brinkmeler M，Nackenhorst U，Petersen S，et al.A Finite Element Approach for the Simulation of Tire Rolling Noise［J］.Journal of Sound and Vibration，2008，309（1／2）：20－39.

［21］Mousseau C W，Hulbert G M.An Efficient Tire Model for the Analysis of Spindle Forces Produced by a Tire Impacting Large Obstacles［J］.Computer Methods in Applied Mechanics and Engineering，1996，135（1／2）：15－34.

［22］Mousseau C W，Hulbert G M.The Dynamic Response of Spindle Forces Produced by a Tire Impacting Large Obstacles in a Plane［J］.Journal of Sound and Vibration，1996，195（5）：775－796.

［23］Mousseau C W，Laursen T A，Lidberg M，et al.Vehicle Dynamics Simulations with Coupled Multibody and Finite Element Models［J］.Finite Elements in Analysis and Design，1999，31（4）：295－315.

［24］HKS Corporation.ABAQUS Theory and User Manual V.6.8［M］.Waltham，MA，USA：Dassault Systems，2008.

［25］Bourgois L.Belt Test for the Evaluation of the Fretting Fatigue and Adhesion Behavior of Steel Cord in Rubber［J］ASTM Special Technical Publication，1979（694）：103－109.

［26］Bourgois L.Survey of Mechanical Properties of Steel Cord and Related Test Methods［J］ASTM Special Technical Publication，1979（694）：19－46.

［27］Zhang Z.Estimate of Endurance Limits of Steel Cord under Different Bending Fatigue Conditions［J］.Wire Journal International，2000，33（10）：116－119.

［28］Usabiaga H，Pagalday J M.Analytical Procedure for Modeling Recursively and Wire by Wire Stranded Ropes Subjected to Traction and Torsion Loads［J］.International Journal of Solids and Structures，2008，45（21）：5503－5520.

［29］Ghoreishi S R，Davies P，Cartraud P，et al.Analytical Modeling of Synthetic Fiber Ropes.Part II：A Linear Elastic Model for 1＋6Fibrous Structures［J］.International Journal of Solids and Structures，2007，44（9）：2943－2960.

［30］Lou A Y C，Walter J D.Interlaminar Shear Strain Measurements in Cord－rubber Composites［J］.Rubber Chemistry and Technology，1979，52（4）：792－804.

［31］Cernik B M.Method of Preparing a Steel Cord for the Measurement of Stress Therein：US，3930918［P］.1976－06－01.