轮毂电机独立驱动电动汽车差速转向路感控制研究

赵万忠 王春燕 张宗强 于蕾艳 赵 婷

1.南京航空航天大学，南京，210016 2.中国石油大学，青岛，266580

0 引言

电动轮汽车采用轮毂电机独立驱动技术，通过控制左右车轮差速转矩，可实现新型差速转向。在电动轮汽车基础上，发展一种新型差速转向系统，使其同时融合主动转向和助力转向功能，不仅能实现汽车轻便转向和驾驶员满意路感的完美融合，还能使汽车的安全性与灵活性协调统一，是一种理想的动力转向技术，具有广阔的应用前景［1－3］。

目前，国内外有关电动轮汽车的研究主要集中在动力学建模与驱动转矩控制方面。文献［4］建立了电动轮汽车整车模型、驾驶员模型和道路模型，对低附着路面和极限概况下的电动轮汽车进行了动力学仿真，并将其与纯电动汽车进行了对比分析。结果表明，电动轮汽车具有更好的操纵稳定性。道路试验也验证了电动轮汽车在极限工况和低附着路面下的稳定性和可靠性。文献［5］根据电动轮汽车驱动／制动力矩独立可控的特点，采用层次化结构的控制分配方法，对电动轮汽车驱动／制动扭矩进行了优化控制来提高车辆的操纵稳定性。

对电动轮汽车的研究目前主要集中在电动轮驱动技术上，对差速助力转向技术的研究还较少，有限的几篇文献主要探讨差速转向原理［6－7］。文献［8］对电动轮汽车差速技术进行了实验研究，验证了电动轮汽车差速系统在各工况下的实际性能，但未针对转向路感等转向性能指标进行优化设计或提出具体控制策略。文献［9］设计了一种自适应模拟退火算法来对差速转向系统的转向路感进行系统参数优化，但并未对转向路感进行实时控制。文献［10］建立了差速转向动力学模型，提出了差速转向驱动转矩控制（包括驱动转矩分配控制和横摆角速度反馈控制）策略，其仿真结果表明，该控制策略能让汽车在不同工况下实现差速转向。文献所涉及的差速转向系统虽具有差速功能，但未涉及动力转向系统的功能，如电动助力转向和主动转向功能。新型差速转向不仅在结构上能实现差速转向功能，还可以通过控制系统的力与位移传递特性，使系统同时融合助力转向和主动转向功能，实现驾驶员路感和汽车操纵稳定性的协调统一，拓展传统动力转向系统的功能。

本文建立了新型差速转向及整车系统的动力学模型，以鲁棒控制理论为基础，设计了新型差速转向H∞－PID鲁棒控制器，研究了新型差速转向路感控制机理。

1 新型差速转向动力学建模

1.1 整车三自由度模型

根据汽车转向特性，汽车三自由度方程为［11］

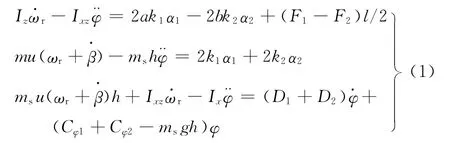
式中，g为重力加速度；u为车速；ωr为横摆角速度；m为整车质量；ms为簧载质量；δ为前轮转向角；α1为前轮侧偏角；α2为后轮侧偏角；φ为车身侧倾角；β为质心侧偏角；l为两前轮之间的距离；a为汽车质心至前轴的距离；b为汽车质心至后轴的距离；h为侧倾力臂；Ix为悬挂质量对X轴的转动惯量；Iz为汽车质量对Z轴的转动惯量；Ixz为悬挂质量对X、Z轴的惯性积；E1为前侧倾转向系数；E2为后侧倾转向系数；Cφ1为前悬架侧倾角刚度；Cφ2为后悬架侧倾角刚度；D1为前悬架侧倾角阻尼；D2为后悬架侧倾角阻尼；k1为前轮侧偏刚度；k2为后轮侧偏刚度；F1、F2为左右车轮的驱动力。

1.2 轮毂电机模型

将三相永磁无刷直流轮毂电机作为电动轮驱动电机，则电机电磁转矩可表示为

式中，Ka为电机转矩系数；iA为电机电流。

左右轮毂电机电磁转矩可分别表示为

式中，T1、T2分别为左右转向轮的驱动转矩。

1.3 输出轴子模型

对转向柱输出轴及电机输出轴进行动力学分析，得到：

对左右转向轮进行动力学分析，可得

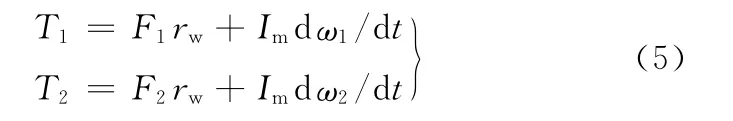
式中，rw为车轮滚动半径；Im为考虑轮毂电机转动惯量的电动轮等效质量；ω1、ω2分别为左右转向轮的转动角速度。

车轮在牵引力控制的作用下，滑转率较小，车轮转动角加速度也可以忽略，则ΔTm可进一步表示为

式中，d为轮胎拖距。

1.4 输入轴子模型

对转向盘和转向输入轴进行动力学分析，得到：

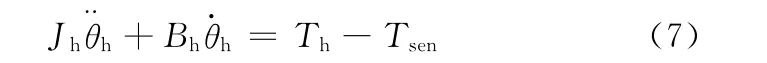
转矩传感器依靠扭杆的相对转动产生扭转变形，扭杆受到的转矩与扭杆的扭转角度成正比：

式中，Ks为与输入轴相连的扭杆的刚性系数；θh为输入轴的转角；θε为输出轴的旋转角。

1.5 齿轮齿条子模型

对齿条和小齿轮进行动力学分析，可得

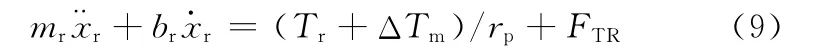
1.6 轮胎模型

假设轮胎的特性是线性的，并忽略转向引起的侧偏刚度变化，可得动力学方程：

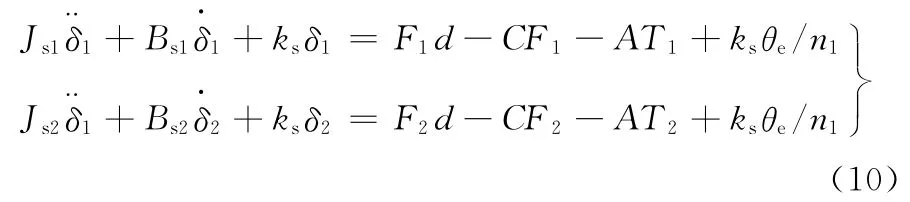
式中，Js1、Js2分别为左右转向轮绕其主销转动惯量；Bs1、Bs2分别为左右转向轮的黏性阻尼系数；δ1、δ2分别为左右转向轮的转向角；A为左右转向轮绕主销的回正阻尼系数；C为左右转向轮绕主销干摩擦因数。

2 路感控制策略

2.1 转向路感

本文采用固定方向盘的方法来分析转向路感：一方面，它能把路面干扰信息完全传递给驾驶员；另一方面，固定方向盘后，转向盘和转向输入轴连为一体，减少了一个自由度，便于分析。

从输出轴转角到输出轴所受阻力矩的传递函数：

式中，Km为左右轮毂电机转矩差增益。

由转向盘固定，可得

联立式（11）、式（12），得到从输出轴所受阻力矩到转向盘输入转矩Th的传递函数（定义为转向路感）：

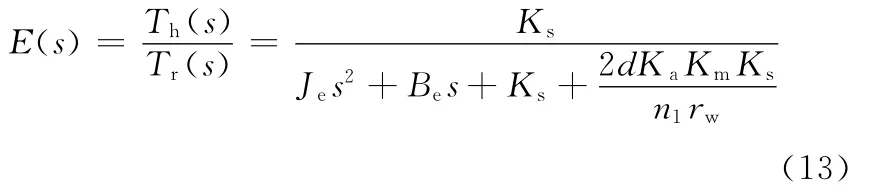
2.2 LMI线性矩阵不等式

从理论上讲，H∞控制理论可以在保证控制系统稳定的前提下，抑制外界干扰对被控对象的影响。该控制方法在转子系统的主动控制中得到了广泛的应用，可以很好地满足系统的跟踪性能和鲁棒稳定性的要求。

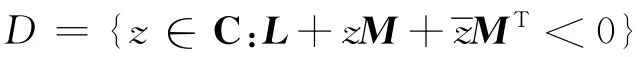
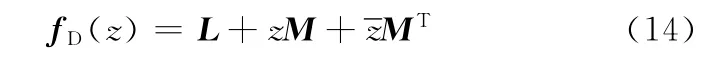
对于扇形区域（顶点在原点，扇角为2θ），矩阵值函数fD（z）满足：

因而，实数矩阵A在扇形区域稳定的充分必要条件是存在一个正定矩阵Xi（i＝1，2，3），使得下列LMI成立［13］：

系统的暂态响应与其极点分布有很大的关系，系统能够稳定的充分必要条件是它的极点分布在复平面的左半平面。当极点分布在一些特定的区域时，能够刻画系统一定的指标S（α，γ，θ），如图1所示。

位于这个区域的点z＝x＋j y，x＜－α＜0，｜x＋j y｜＜r，xtanθ＜－｜y｜。把极点配置在这个区能够确保系统有很小的衰减度α，有最小的阻尼ζ＝cosθ，有最大的阻尼振荡频率ωd＝rsinθ。

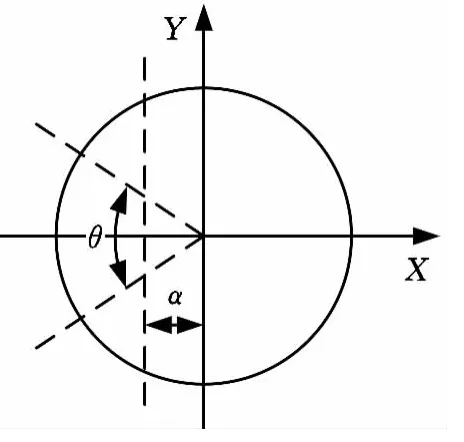
图1 扇形区域图

2.3 H∞性能指标

考虑线性时不变的连续时间系统［14］：

式中，x（t）表示系统的状态，x（t）∈ Rn；w（t）表示外部扰动输入，w（t）∈ Rq；z（t）为系统期望输出，z（t）∈ Rr。

由式（17）可得系统从ω到z的传递函数T（s）＝C（sI－A）－1B＋D，T（s）的H∞范数定义为其频率响应的最大奇异值的峰值，即

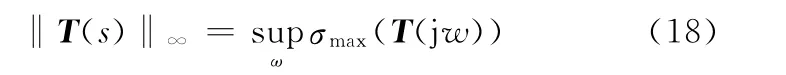
对于上述系统，设γ＞0是一个给定的常数，则以下条件是等价的：①系统渐进稳定且‖T（s）‖＜γ；②存在一个对称矩阵P＞0，使得

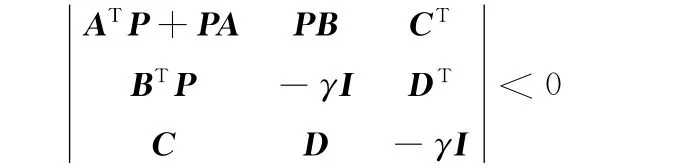
2.4 基于LMI的H∞鲁棒PID路感控制

以路感函数为控制对象，对路感设计基于LMI的H∞鲁棒PID控制器，其结构如图2所示。其中，r为输入；e为偏差量；u为控制输入；w为零均值高斯白噪声，其强度W ＞0，初始状态x（0）与w 不相关；y为输出；C（s）为PID控制器；E（s）为转向路感的传递函数，本转向系统的路感函数是可观的，其形式为

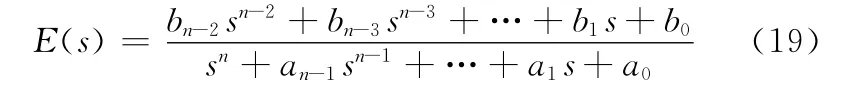
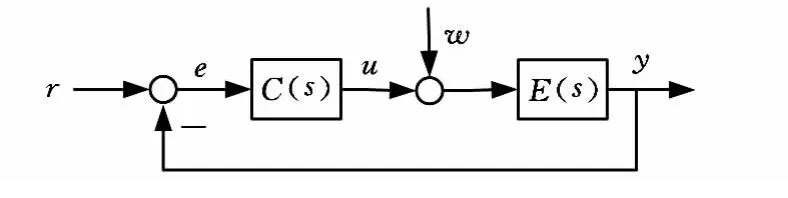
图2 系统结构图

PID控制器参数K＝［KPKIKD］对于系统满足：①系统的闭环极点落在图1所示的扇形区域内，并且存在正定矩阵Xi（i＝1，2，3），使得系统稳定性条件（式（16））成立；②从扰动w到被控输出的传递函数矩阵满足‖H（s）‖∞＜γ。

如果存在正定矩阵Q使以下线性矩阵不等式组有解

则PID控制器的参数为

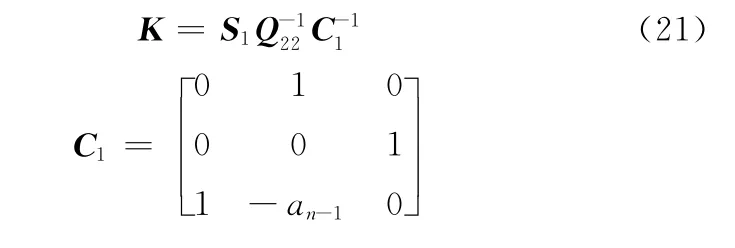
3 仿真分析

转向路感是转向系统的一个重要的评价指标，满意的转向路感可以令驾驶员准确接收来自于路面的信息，从而作出准确的判断，避免事故的发生。为了能有效地分析转向系统的动态特性，采用固定转向盘的方法，研究转向盘固定时作用在扭杆上的转向盘把持转矩，该把持转矩实质上是转向轮来自地面的干扰。

对于本路感系统，要求其极点处于LMI区域左半平面内，取α＝0，θ＝45°。取H∞范数γ＝0.1，取扇形区域D的半径r＝3000。代入式（20），得到 PID 控 制 器 的 参 数 KP＝133.5752，KI＝0.0001，KD＝0.0058。则路感控制后效果如图3所示。

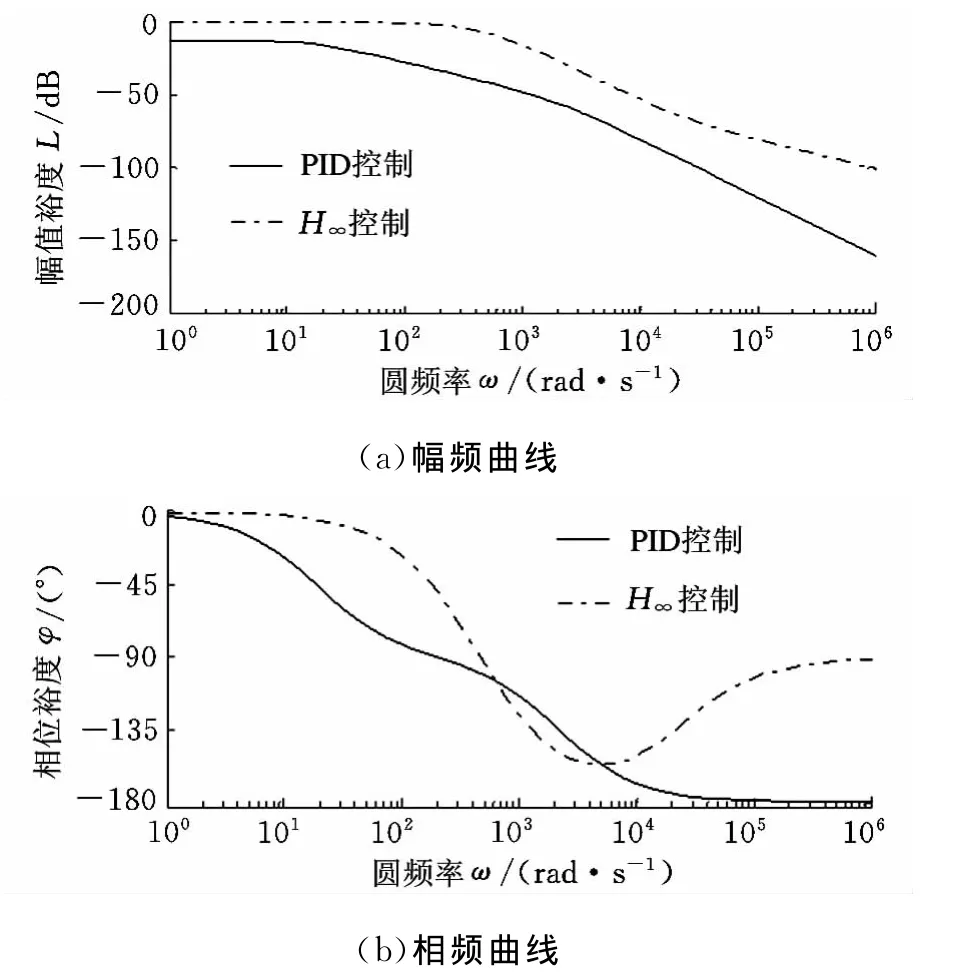
图3 控制后路感闭环bode图

对比不同控制下的转向盘把持转矩幅频特性和相频特性可知：控制后，新型差速转向系统的静态误差进一步减小，响应进一步变快，频带进一步变宽，相频带较优化前变宽，系统响应速度加快，零频幅比增大，系统精度进一步增大。由图3还可以看出，低频情况下，转向盘把持转矩的幅值几乎维持不变，且H∞－PID控制时的频带更宽、幅值更大，可保证驾驶员获得更好的低频有效信息；高频情况下，H∞－PID控制对高频的路面噪声和干扰抑制较快，有利于驾驶员获得较为满意的路面感觉。

由此可知，基于LMI的H∞－PID路感控制器可使新型差速转向获得：①更小的静态误差；②更好的低频有效信息；③更好地抑制路面噪声和干扰，从而有效优化系统的转向路感。

4 结语

为了改善电动轮汽车差速转向系统的转向路感，构建了汽车三自由度模型及差速转向系统模型。基于LMI矩阵不等式，设计了鲁棒PID路感控制器，并进行了转向路感仿真试验。仿真结果表明，基于LMI的H∞－PID控制器能够较好地优化电动轮差速转向系统的转向路感，既使系统具有理想的转向灵敏度和转向稳定性，又实现了驾驶员路感和汽车主动安全性的完美结合。

［1］陈勇，陈中奎，周秋丽.两后轮驱动的电动轮汽车的动力学建模与仿真分析［J］.汽车安全与节能学报，2010，1（2）：158－162.Chen Yong，Chen Zhongkui，Zhou Qiuli.Dynamic Modeling and Simulation Analysis of an Electric Vehicle with Two Rear Hub－motors［J］.Journal of Automotive Safety and Energy，2010，1（2）：158－162.

［2］赵万忠，孙培坤，刘顺.力与位移耦合控制的主动转向系统协同优化［J］.机械工程学报，2012，48（18）：112－116.Zhao Wanzhong，Sun Peikun，Liu Shun.Collaborative Optimization of Active Steering System with Force and Displacement Coupled Control［J］.Chinese Journal of Mechanical Engineering，2012，48（18）：112－116.

［3］Kim J H，Song J B.Control Logic for an Electric Power Steering System Using Assist Motor［J］.Mechatronics，2002，12（3）：447－459.

［4］Mutoh N，Nakano Y.Dynamics of Front－andrear－wheel－independent－drive－type Electric Vehicles at the Time of Failure［J］.IEEE Transactions on Industrial Electronics，2012，59（3）：1488－1499.

［5］余卓平，姜炜，张立军.四轮轮毂电机驱动电动汽车扭矩分配控制［J］.同济大学学报（自然科学版），2008，36（8）：1115－1119.Yu Zhuoping，Jiang Wei，Zhang Lijun.Torque Distribution Control for Four Wheel In－wheel－motor Electric Vehicle［J］.Journal of Tongji University（Natural Science），2008，36（8）：1115－1119.

［6］Kim W，Yi K，Lee J.Drive Control Algorithm for an Independent 8In－wheel Motor Drive Vehicle［J］.Journal of Mechanical Science and Technology，2011，25（6）：1573－1581.

［7］Kang J，Yoo J，Yi K.Driving Control Algorithm for Maneuverability，Lateral Stability，and Rollover Prevention of 4WD Electric Vehicles with Independently Driven Front and Rear Wheels［J］.IEEE Transactions on Vehicular Technology，2011，60（7）：2987－3001.

［8］靳立强，王庆年，张缓缓.电动轮驱动汽车差速性能试验研究［J］.中国机械工程，2007，18（21）：2632－2636.Jin Liqiang，Wang Qingnian，Zhang Huanhuan.Experimental Study on the Differential Capability of Motorized Wheels Driving Vehicles［J］.China Mechanical Engineering，2007，18（21）：2632－2636.

［9］王春燕，赵万忠，赵婷，等.电动轮汽车差速助力转向系统路感优化［J］.中国机械工程，2012，23（1）：122－125.Wang Chunyan，Zhao Wanzhong，Zhao Ting，et al.Road Feel Optimization of Differential Steering of E－lectric Vehicle with Motorized Wheels［J］.China Mechanical Engineering，2012，23（1）：122－125.

［10］Wang J，Wang Q，Jin L，et al.Independent Wheel Torque Control of 4WD Electric Vehicle for Differential Drive Assisted Steering［J］.Mechatronics，2011，21（1）：63－76.

［11］Zhao W Z，Wang C Y，Sun P K，et al.Primary Studies on Integration Optimization of Differential Steering of Electric Vehicle with Motorized Wheels Based on Quality Engineering［J］.Science China Technological Sciences，2011，54（11）：3047－3053.

［12］Fang C H，Liu Y S.A New LMI－based Approach to Relaxed Quadratic Stabilization of T－S Fuzzy Control Systems［J］.IEEE Transactions on Fuzzy System，2006，14（3）：120－124.

［13］Gao J F，Yu L，Wang C P.An LMI－based Nonlinear Attitude Control Approach ［J］.IEEE Transactions on Control Systems Technology，2003，11（1）：73－83.

［14］Chen X Q.Optimal Control for Electrical Powerassisted Steering System［D］.Windsor：University of Windsor，2005.