细菌群觅食优化算法及PID参数优化应用

陈东宁 张国峰 姚成玉 张瑞星

1.燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，066004

2.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

3.燕山大学河北省工业计算机控制工程重点实验室，秦皇岛，066004

0 引言

近年来，人们模拟自然界生物群体行为发展出一系列群体智能仿生算法，其中，粒子群优化（particle swarm optimization，PSO）算法和细菌觅食（bacterial foraging，BF）算法已在诸多领域展现了良好的应用前景。

PSO算法具有概念简明、实现方便、收敛速度快等优点，在很多优化问题中得到成功应用。文献［1］将PSO算法应用于可靠性优化，并通过串－并联、桥式系统等可靠性优化实例验证了方法的可行性。文献［2］将混沌粒子群优化的神经网络应用于旋转机械故障诊断，取得了良好效果。然而，PSO算法在求解优化问题时，容易陷入局部 最 优，引 起 早 熟 收 敛［3］。BF 算 法 是 由Passino［4］提出的一种新型仿生类算法，具有并行搜索、易跳出局部极小值等优点，在不同领域得到了广泛应用。文献［5］将变邻域BF算法用于求解作业车间调度问题，为车间调度问题提供了有效方法。文献［6］将BF算法应用于公交调度优化，实现了交通系统的优化配置，但该算法存在收敛速度慢的缺点。

近几年有学者将PSO算法和BF算法融合，如Biswas等［7］提出了一种混合PSO细菌觅食算法——BSO算法，即在细菌趋化操作后对细菌执行了一个仅使用全局最佳粒子的趋化前进操作，该算法优于BF算法和标准PSO算法。然而，BSO算法趋化前进操作中没有考虑个体最佳粒子这一因素。

为此，本文提出一种细菌群觅食优化（bacterial swarm foraging optimization，BSFO）算法，利用PSO算法中粒子的速度更新公式来替代BF算法位置公式中的方向向量，并通过测试函数和控制系统仿真验证其优化效果。

1 细菌群觅食优化算法

1.1 PSO算法

PSO算法将系统初始化为一组随机解，通过迭代搜寻最优值，粒子在解空间追随最优的粒子进行搜索。每一次迭代中，粒子通过跟踪2个“极值”来进行自我调整，一个极值是粒子本身所经历过的最优解，称为个体最佳位置pbest，另一个极值是整个种群目前找到的最优解，称为全局最佳位置gbest。粒子在第k代的速度和位置更新过程如下［8］：

式中，vk、xk分别为第k代更新中粒子的速度和位置；vk＋1、xk＋1分别为第k＋1代更新中粒子的速度和位置；r1、r2为［0，1］区间内的随机数；c1、c2为加速常数，代表将每个粒子推向pbest和gbest位置的统计加速项的权重，通常取为常数2；w为惯性权重。

式（1）、式（2）中的位置和速度不同于物理学中的含义，具有相同量纲，可以直接相加，下同。

惯性权重w表征上一代的速度对当前代速度的影响程度。随着迭代次数的增加，粒子离最优点越来越近，为了减小振荡，希望速度越来越小。为此，通常采用如下方式来调整惯性权重w：

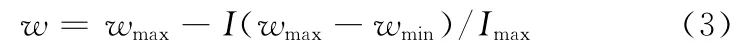
式中，I为当前迭代次数；Imax为最大迭代次数；wmax、wmin分别为惯性权重的最大值和最小值［9］。

1.2 BF算法

细菌群的觅食行为可以看作是不断优化的过程，优化问题的解对应搜索空间内细菌的状态，即优化函数适应度值。BF算法包括趋化、繁殖、驱散三个步骤。

1.2.1趋化

趋化是细菌朝含有营养的区域聚集的行为。趋化过程中，细菌运动模式包括翻转和前进。翻转是细菌向随机方向移动单位步长，每当细菌完成一次翻转后，检查适应度值是否改善，若是，则细菌将沿同一方向继续前进Ns步。趋化的位置更新公式为

式中，Pi（j，k，l）为第i个细菌在第j次趋化、第k次繁殖和第l次驱散中的位置；Δ（i）为随机产生的方向向量；C（i）为细菌在任意方向被指定的步长大小。

1.2.2繁殖

所有细菌完成趋化后，进入繁殖阶段。采用健康度作为评定各细菌优劣的准则，计算公式为

式中，Jh，i为第i个细菌的健康度；ji（j，k，l）为第i个细菌在第j次趋化、第k次繁殖和第l次驱散操作中的适应度值；Nc为趋化步骤的最大次数。

将全部S个细菌根据健康度进行升序排序，淘汰健康度较差的Sr（Sr＝S／2）个细菌，保留健康度较好的Sr个细菌。将存活的Sr个细菌以一分为二的方式进行繁殖，产生的子细菌具有和母细菌相同的位置和趋化步长。

1.2.3驱散

细菌在Nre次繁殖结束后，将适应度值差的细菌驱散。为确保细菌总数的不变，以概率Ped驱散相同数目的细菌到其他位置，剩余细菌的位置保持不变。细菌驱散步骤的最大次数为Ned。

1.3 BSFO算法的提出

BF算法中，一个细菌代表一个解，细菌在寻找最优解时只依靠自己，群体间不存在信息共享机制。PSO算法中，一个粒子代表一个解，粒子在寻找最优解时，不仅依靠自身，也依靠其他的信息（个体历史最优解和全局最优解）。针对这种情况提出了BSFO算法，即通过借鉴PSO算法中粒子之间的信息共享机制，利用PSO算法中粒子的速度更新公式来代替细菌趋化中翻转操作的位置公式中的方向向量Δ（i），使细菌在更新自身运动位置时，不断感知周围同伴的位置信息及细菌群体的历史最优位置信息，进而克服PSO算法存在早熟收敛和BF算法收敛速度慢的缺陷。

将式（1）代入式（4），可得

为提高算法在优化前期的全局搜索能力和优化后期的局部搜索能力，趋化步长不再像BF算法中设为固定值，而改设为动态调整值：

式中，C（k，l）为第k次繁殖和第l次驱散的趋化步长；Lred为初始趋化步长；nk＋l－1为第k＋l－1次控制步长下降梯度的参数。

由于C（k，l）是随繁殖操作数k和驱散操作数l增加而下降的函数，当初期的k、l较小时，步长C（k，l）较大，以便在较大的空间内搜索解。进化的过程中，随着k、l逐渐增大，步长C（k，l）减小，使细菌在较好解的附近进一步搜索最优解，保证算法最终趋近全局最优点。

BSFO算法步骤如下：

（1）初始化细菌位置、速度。

（2）评价适应度值。

（3）三层循环。最内层步骤是趋化，其中，细菌的运动模式为翻转，以式（6）进行细菌位置更新；前进，更新个体最优和全局最优并用式（1）更新各细菌的速度。中间层步骤是繁殖。最外层步骤是驱散。

（4）输出最优解。

BSFO算法以BF算法为基础，在趋化时用PSO算法中粒子的速度更新公式（式（1））来代替细菌趋化公式（式（6））中随机产生的方向向量Δ（i）。有目的的方向操作加快了细菌的收敛，全局最优的引导作用提高了算法的精度。同时，舍去PSO算法中的式（2），直接用式（6）计算细菌位置更新历史最优值。

1.4 BSFO算法的Benchmark函数测试

为分析所提的BSFO算法搜索性能，以BF算法、μPSO 算 法［10］和 BSO 算 法［7］作 为 对 比 算法。其中，μPSO算法的原理是通过对一般粒子和当代最优粒子设置不同的速度、位置计算公式增强粒子的搜索能力，利用排斥项避免搜索进程陷入早熟状态，从而有效提高PSO算法的优化效率。

选择表1所示的8个Benchmark函数对上述4种算法进行数值试验，这些函数广泛应用于评价优化算法的性能。评价的标准包括优化结果的平均值和标准差，平均值反映了在给定迭代次数下算法所能达到的精度，标准差反映了算法的稳定性。

分别用BF算法、μPSO算法、BSO算法和BSFO算法优化上述8个测试函数，程序重复运行30次所得函数极值的平均值和标准差见表2。从表2可以看出，与其他三种算法相比，BSFO算法对大部分测试函数更接近所求极值，标准差较小，具有较高的精度和稳定性。

表1 8个测试函数

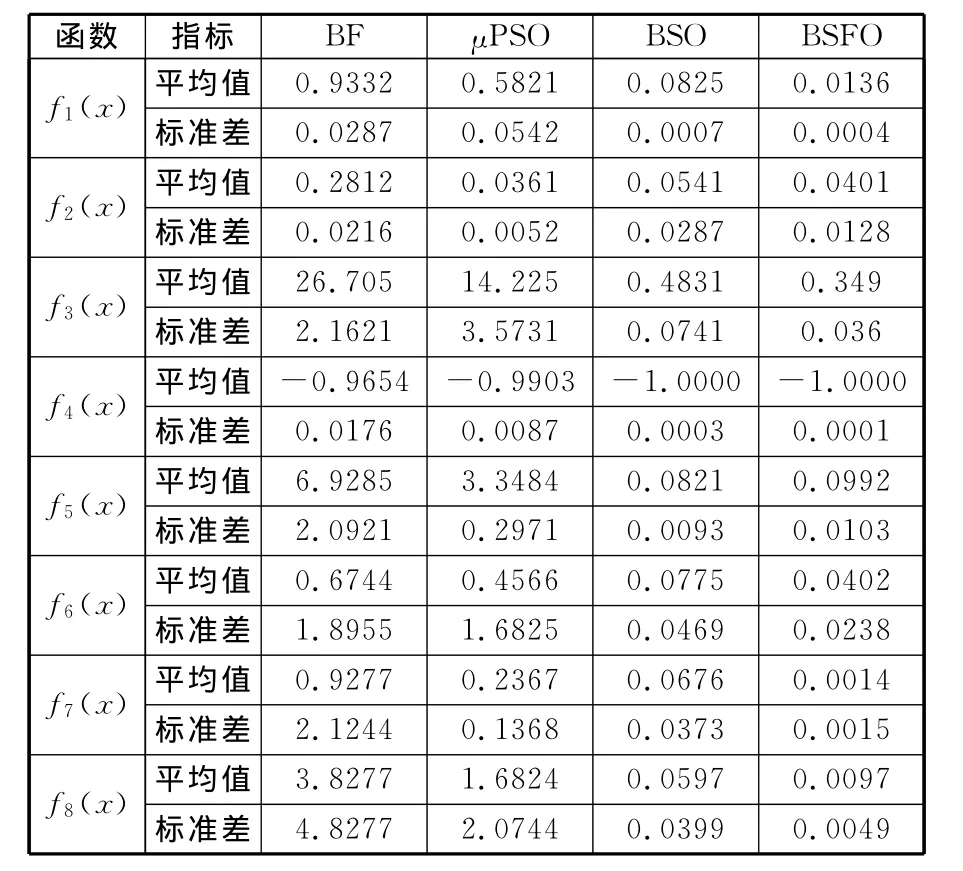
表2 4种算法所得优化结果

这4种算法运行30次的运行时间平均值和标准差见表3。

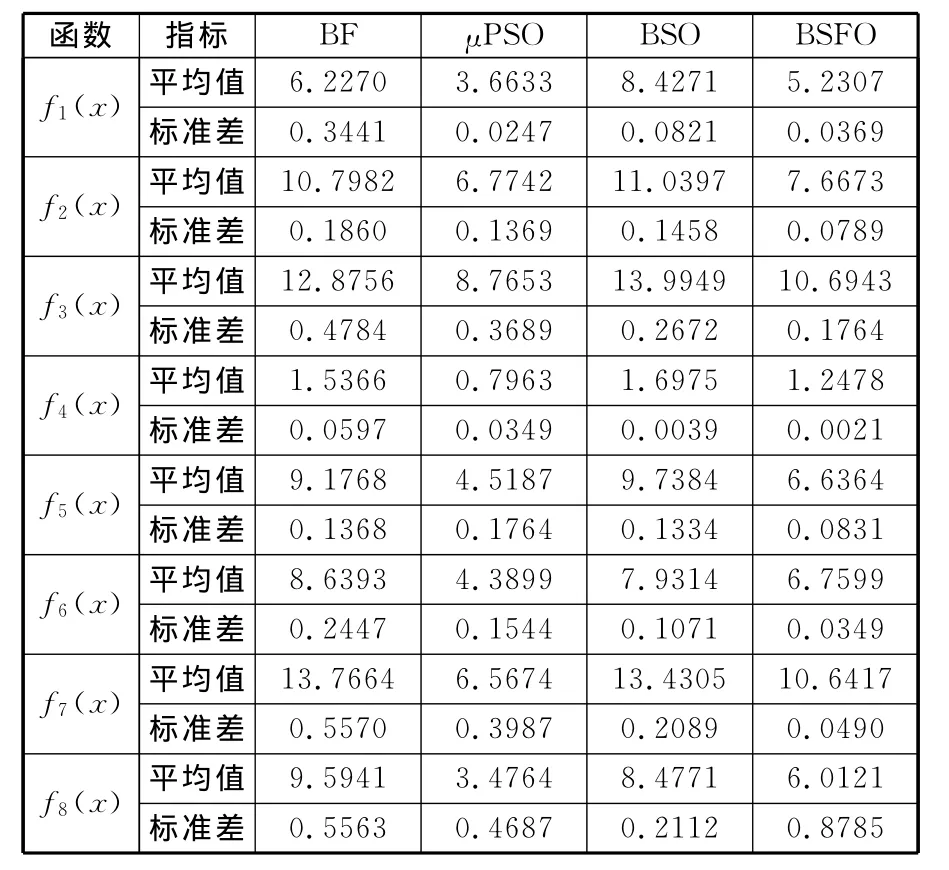
表3 4种算法运行时间的平均值和标准差 s

从表3可以看出：基本BF算法与BSO算法在时间消耗上是差不多的，BSFO算法比上述两种算法耗时更少，μPSO耗时最少。综合表2、表3可以看出，BSFO算法不仅具有较高求解精度，而且耗时较少。

2 材料试验机PID控制器参数优化

2.1 电液位置伺服系统数学建模

以材料试验机电液位置伺服系统为研究对象，运用BSFO算法对其PID控制器参数进行优化。材料试验机电液位置伺服系统原理如图1所示，图2为系统控制框图。

图1 材料试验机电液位置伺服系统示意图

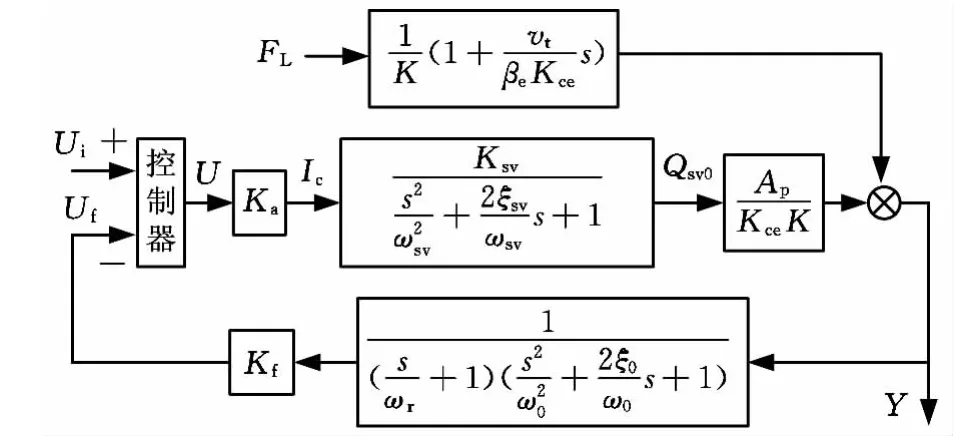
图2 电液位置伺服系统框图

忽略外力扰动FL，得到开环传递函数：

式中，Uf为传感器反馈电压；U为控制器输出电压；Ka为伺服放大器增益；Ksv为伺服阀流量增益系数；Ap为液压缸活塞有效面积；Kf为位移传感器增益；Kce为总流量－压力系数；K为负载弹簧刚度；ωsv为伺服阀固有频率；ξsv为伺服阀阻尼比；ωr为惯性环节转折频率；ω0为综合固有频率；ξ0为综合阻尼比。

将材料试验机电液位置伺服系统实际参数代入后得到开环传递函数：

作出系统的开环Bode图（图3），其幅值裕度为56dB，相位裕度为无穷大，可见该系统闭环稳定。

计算该系统在1V指令（10mm）下闭环阶跃响应，如图4所示。可以看出，该系统在未加任何补偿控制器之前，虽然系统闭环稳定，但是存在较大的静态误差，且响应很慢，远不能达到该材料试验机对准确性的要求，因此必须设计合理的控制器才能使得该系统到达一定的使用要求。

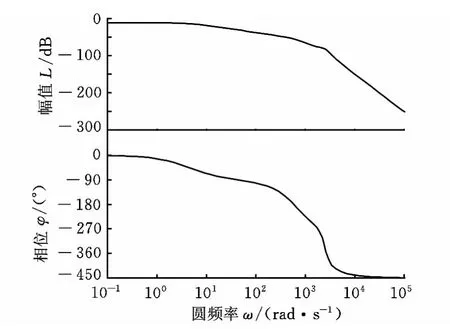
图3 系统的开环Bode图

图4 闭环系统的阶跃响应

2.2 数字PID控制器

数字计算需要对常规的PID算式通过采样进行离散化，离散化后的控制器即为数字PID控制器。数字PID控制器可分为位置式和增量式，增量式算法系统工作会更安全。一旦计算机出现故障，使控制信号Δu（kT）为零时，执行机构的位置仍能保持前一步的位置u（kT），从而对系统安全不会有大的影响。因此，采用增量式数字PID控制器，表达式如下：

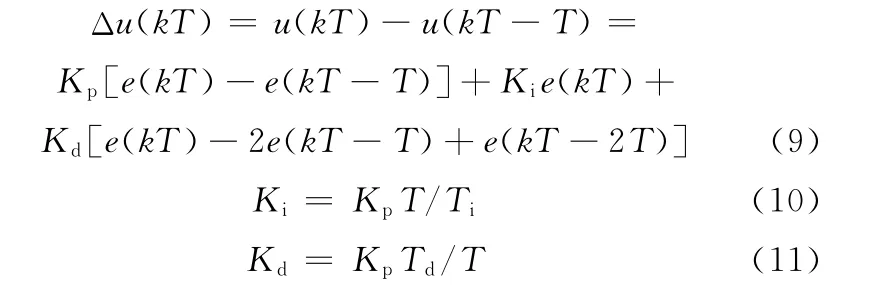
式中，u为控制输出；e为误差；Kp为比例系数；Ki为积分系数；Kd为微分系数；T为采样周期，T＝0.001s；Ti为积分时间常数；Td为微分时间常数。

2.3 基于BSFO算法的PID控制器参数优化

细菌位置量P（式（1）中的x）编码为［Kp，Ki，Kd］，即为PID控制器的3个调节参数。目标函数包括绝对误差、控制器输出平方、被控对象输出增量和调节时间等。构造目标函数：

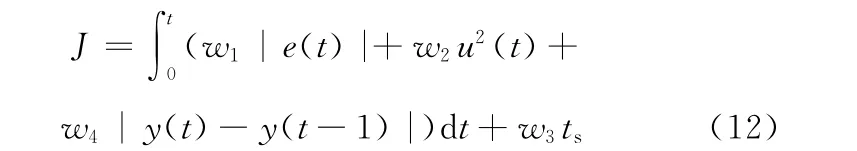
式中，e（t）为控制误差；u（t）为控制器输出；ts为调整时间；w1、w2、w3、w4为 权 值，w1＝ 0.999，w2＝ 0.001，w3＝2，w4＝100；y（t）为被控对象输出。

BSFO－PID算法流程如图5所示。

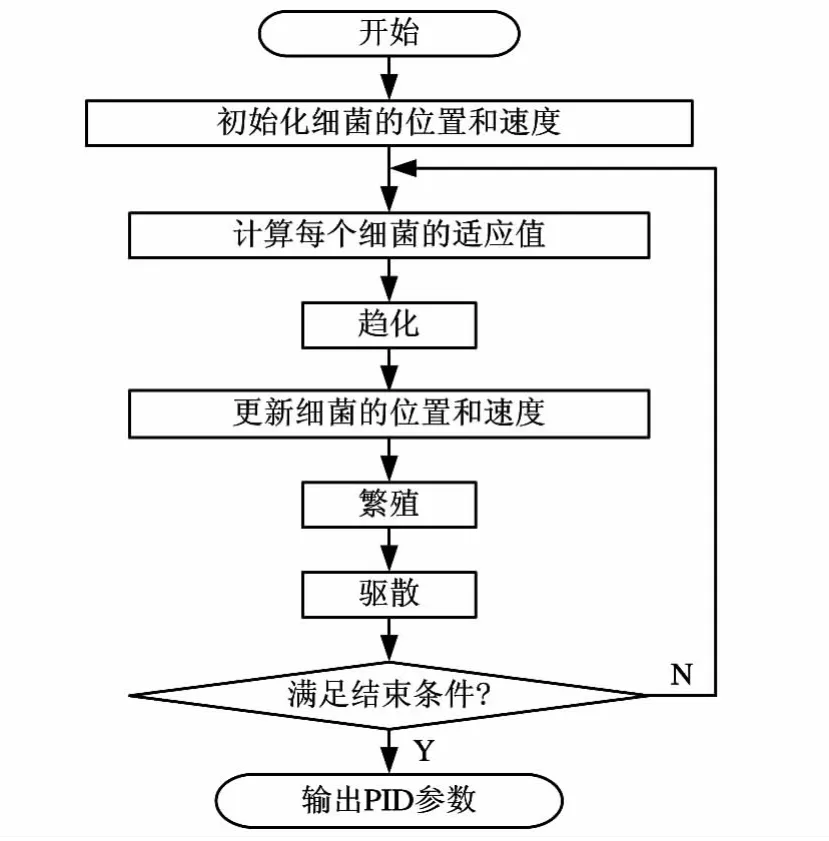
图5 BSFO－PID算法流程

3 仿真结果及分析

BSFO－PID的参数设置如表4所示。最后求得PID控制器的参数和目标函数值的优化结果，如表5所示。从表5可以看出，BSFO－PID控制器的目标函数值最小。

表4 BSFO算法参数设置

表5 不同算法参数优化结果

Z－N PID、BSO－PID、μPSO－PID、BFPID和BSFO－PID几种控制策略作用下控制器的输出量如图6所示。

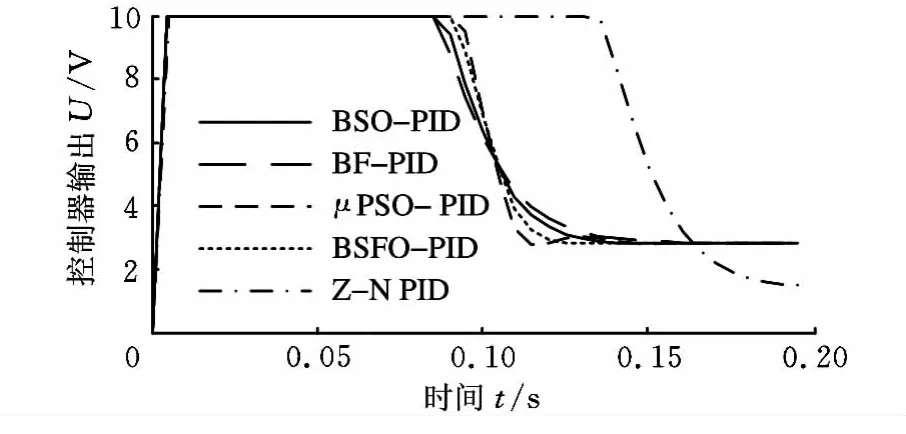
图6 不同控制策略下的控制器输出

材料试验机的电液位置伺服系统的单位阶跃响应（1V，10mm）如图7所示。

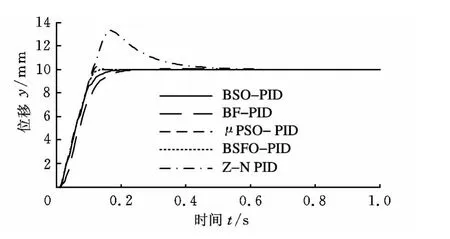
图7 不同控制策略的阶跃响应

系统动态性能指标如表6所示。

表6 阶跃响应动态性能指标

仿真结果表明：运用BSFO算法优化的材料试验机电液位置伺服系统PID控制器较其他4种算法设计的控制器在响应速度、收敛精度、超调量等方面具有更优良的综合控制性能。

4 结论

（1）Benchmark函数测试结果表明：BSFO算法比BF算法、μPSO算法及BSO算法在收敛速度和计算精度上更为理想，克服了PSO算法早熟易陷入局部最优和BF算法收敛速度慢的缺陷。

（2）将BSFO算法应用于材料试验机电液位置伺服系统的PID控制器参数的寻优，通过仿真可得：与Z－N整定算法、BF算法、μPSO算法和BSO算法相比，应用BSFO算法寻优后的PID控制系统具有更好的控制性能，满足了材料试验机的电液位置伺服系统控制性能要求。

［1］Zhao J H，Liu Z H，Dao M T.Reliability Optimization Using Multiobjective Ant Colony System Approaches［J］.Reliability Engineering and System Safety，2007，92（1）：109－120.

［2］仇国庆，唐贤伦，庄陵，等.基于混沌粒子群优化的神经网络在旋转机械故障诊断中的应用［J］.中国机械工程，2008，19（21）：2642－2645.Qiu Guoqing，Tang Xianlun，Zhuang Ling，et al.Application of Neural Network Trained by Chaos Particle Swarm Optimization to Fault Diagnosis for Rotating Machinery［J］.China Mechanical Engineering，2008，19（21）：2642－2645.

［3］魏峰涛，宋俐，李言，等.基于改进粒子群算法的四辊轧机机座结构优化设计［J］.中国机械工程，2012，23（19）：2361－2365.Wei Fengtao，Song Li，Li Yan，et al.Optimal Structural Design of 4－roller Rolling Mill Frame Based on an IPSO Algorithm［J］.China Mechanical Engineering，2012，23（19）：2361－2365.

［4］Passino K M.Biomimicry of Bacterial Foraging for Distributed Optimization and Control［J］.IEEE Control Systems Magazine，2002，22（3）：52－67.

［5］易军，李太福.求解作业车间调度的变邻域细菌觅食优化算法［J］.机械工程学报，2012，48（12）：178－183.Yi Jun，Li Taifu.Bacterial Foraging Optimization Algorithm Based on Variable Neighborhood for Job－shop Scheduling Problem［J］.Chinese Journal of Mechanical Engineering，2012，48（12）：178－183.

［6］高政威，庞哈利，汪定伟.基于菌群自适应觅食的公交调度建模仿真与优化［J］.系统仿真学报，2011，23（6）：1151－1155，1160.Gao Zhengwei，Pang Hali，Wang Dingwei.Adaptive Bacterial Foraging Optimization and Its Application for Bus Scheduling［J］.Journal of System Simulation，2011，23（6）：1151－1155，1160.

［7］Biswas A，Desgupta S，Das S，et al.Synergy of PSO and Bacterial Foraging Optimization－A Comparative Study on Numerical Benchmarks［J］.Innovations in Hybrid Intelligent Systems，Advances in Soft Computing.，2007，44：255－263.

［8］陈东宁，姜万录，王益群.基于粒子群算法的冷连轧机轧制负荷分配优化［J］.中国机械工程，2007，18（11）：1303－1306.Chen Dongning，Jiang Wanlu，Wang Yiqun.Load Distribution Optimization of Tandem Cold Mill Based on PSO Algorithm［J］.China Mechanical Engineering，2007，18（11）：1303－1306.

［9］Shi Y，Eberhart R.A Modified Particle Swarm Optimizer［C］／／IEEE International Conference on Evolutionary Computation.Anchorage，1998：69－73.

［10］Huang T，Mohan A S.Micro－particle Swarm Optimizer for Solving High Dimensional Optimization Problems（μPSO for High Dimensional Optimization Problems）［J］.Applied Mathematics and Computation，2006，181（2）：1148－1154.