两种自适应噪声抵消算法的性能仿真＊

（91917部队 北京 102100）

1 引言

传统滤波器如经典的维纳滤波器、卡尔曼滤波器，在进行噪声消除等一系列信号处理过程时，均要求已知信号和随机噪声的相关函数或功率谱密度等统计先验知识。而自适应滤波器可以跟随输入信号和噪声特性自动调整参数，不需要事先得知噪声统计特性，因此日益受到重视。各种自适应算法层出不穷，并在硬件平台上实现，其优异性能已经得以验证。自适应噪声抵消系统（Adaptive Noise Cancellation，ANC），就是将自适应滤波器应用于噪声消除的延伸和拓展。尤其对于强背景噪声中的弱信号检测与恢复，有着传统滤波方法所不能比拟的优越性［1～3］。

2 自适应噪声抵消的原理和算法

在自适应滤波器中，若x（n）、y（n）分别为n时刻的输入、输出信号，d（n）为期望响应，e（n）为误差信号，即e（n）＝d（n）-y（n），参数会根据事先确定的某种最佳准则和e（n）的值而自动调整，使输出信号y（n）更加接近d（n）。滤波器滤波效果的关键在于所采用自适应算法的优劣。LMS算法基于最小均方误差准则，收敛后的滤波器权系数向量满足使输出信号与期望响应之间的均方误差最小的要求。它采用梯度最陡下降法，在迭代的每一步根据实时数据估计梯度矢量，按照设定的步长更新权系数值，直到找到使输出信号和期望响应之间均方误差最小的权值为止［2～4］。

以权值为w（n）的横向滤波器为例，LMS算法的迭代公式为w（n＋1）＝w（n）＋2μe（n）x（n），其中μ＞0，称为收敛因子，即自适应迭代的步长。而为了降低输入信号功率对自适应滤波性能的影响，归一化LMS算法（或称NLMS算法）将步长或收敛因子μ除以输入信号的方差，相应的迭代公式［4～5］为w（n＋1）＝w（n）＋因此NLMS算法的流程与LMS算法基本相同，只是在更新权系数向量前要计算方差的估计值。

自适应噪声抵消系统的核心部分是自适应滤波器和合适的滤波算法。自适应滤波器有两路输入，一路为原始输入，另一路为参考输入，不存在期望响应信号。将被噪声污染的有用信号接到原始输入端，从噪声源提取的噪声接到参考输入端，这样自适应滤波器就根据参考输入的噪声估计出混合信号里的噪声，再和原始输入端的信号进行抵消，从而恢复出有用信号，达到滤除噪声的目的［6～10］。

3 LMS和NLMS算法的仿真分析

接下来在Matlab中编写程序，使用LMS算法和NLMS算法来进行噪声抑制的仿真分析对比，并探讨各种参数的变化对算法性能的影响。

首先，设定滤波器阶数为4，步长为0．01，有用信号是载波频率40Hz，幅度为1 的MSK 信号s（n），待抵消的噪声和参考输入均为同一路服从高斯分布的随机白噪声序列n0（n），功率为1。经过2000次迭代运算，仿真结果如图1所示。

图1 LMS算法的噪声抵消效果

图中曲线a为原始输入信号x（n）＝s（n）＋n0（n），b为噪声抵消器的输出信号y（n），c为有用信号s（n），d则为噪声抵消器的均方误差，即E｛［y（n）-s（n）］2｝。可以清楚地看出，已经被噪声严重污染的信号经过自适应噪声抵消系统后，有用信号被全部保留下来，而绝大部分噪声得到了有效的抑制。虽然与纯粹的MSK 信号相比，输出信号波形还有少许毛刺，说明少量残余噪声仍然没被消除，但是残余噪声功率很小，经过2000次迭代后，输出信号与有用信号的误差均方值基本趋于0。

图2 步长变化时的均方误差曲线

然后，可以通过修改LMS自适应算法的参数，讨论其对滤波器性能的影响。

1）输入信号和滤波器其他参数不变，步长因子分别为0．001、0．005和0．01时，均方误差曲线如图2所示，反映出步长的选择对自适应算法的各项性能影响很大，当步长因子从0．001 变到0．01后，达到稳定状态的迭代次数从1200次迅速降为200次，自适应算法的学习时间也大为降低，但是这种收敛速度的提高是以牺牲稳态时的均方误差为代价的。步长的加大造成滤波器最后失调系数的增加，滤波器消除噪声的效果也略有下降。

2）其他条件不变，步长因子为0．01，滤波器的阶数分别为4、8、16时，均方误差曲线如图3所示。当步长固定不变时，随着滤波器所采用阶数的增加，系统达到稳定收敛状态的均方误差也在提高，相应的自适应学习时间也不断拉长，使得滤波器的性能恶化。

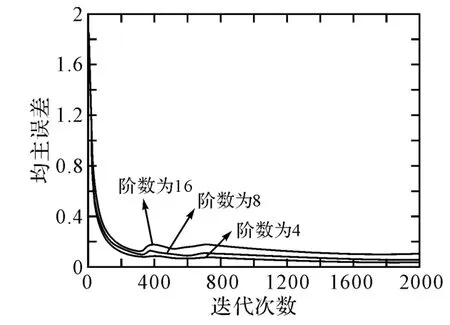
图3 均方误差与滤波器阶数之间的关系曲线

3）将参考输入噪声换成另外一路Matlab随机生成的高斯白噪声序列，其余条件不变，经过仿真，滤波效果如图4所示。

图4 两路输入噪声不相关时的系统性能

图4中的四个子图从上到下依次表示原始输入端、输出端信号、有用信号和滤波器均方误差曲线。可以发现，经过自适应噪声抵消系统，噪声不仅一点没有被清除或削弱，反而有增强的趋势。这是因为两路不相关的高斯白噪声实际上统计独立，参考输入端的信号和待抵消的噪声分量一点也不相关，自适应滤波器就不能够将其加工成待抵消的噪声来和原始输入信号相减。这个例子充分说明了自适应噪声抵消系统能正常工作的一个必要条件就是参考输入端信号一定要与原始输入信号中的噪声相关。相反，如果参考输入端的信号不仅与噪声相关，还和有用信号有一定的相关性，再次进行仿真，保持其余条件不变，只将原来的参考输入噪声再叠加cos（πt／2Ts），Ts是有用MSK 信号的码元持续时间，由于MSK 被认为可以分解成两路正弦加权的OQPSK 信号之和，cos（πt／2Ts）正是其加权函数。通过这样的方式，建立起与有用信号相关的参考输入噪声。最后抵消的结果如图5所示，虽然原始输入中的白噪声绝大部分已经清除掉，但是滤波器也削弱了有用信号，最后输出的波形与纯粹的MSK 相比，有很明显的失真，收敛后的均方误差值一直保持在0．5以上，并无递减趋于0的势头。因此参考噪声的选取是否恰当是影响系统消噪效果的一个关键问题。

图5 参考噪声与有用信号相关时的消噪效果

当原始输入为幅度均为1的MSK 信号和噪声n0＝cos（1．24t）的混合信号，参考输入噪声幅度是n0的5倍，但相位比n0领先π／4，即n1＝5cos（1．24t＋π／4），这样，输入信号的自相关矩阵就与白噪声时的对角线矩阵有一定差别，滤波器阶数为4，步长均为0．01，NLMS算法的φ值设定为0．001，经过2000次迭代，采用LMS 和NLMS 算法的自适应噪声抵消系统消噪效果分别如图6和7所示，两张图中四幅子图曲线所代表含义与图5相同。观察这两张图片，可以很明显地发现LMS算法的输出信号与有用信号相差很大，基本上被噪声完全破坏掉，根本无法从中检测出有用信号，而且均方误差在经过一定时间的迭代后，维持在0．5左右出现振荡，不能进一步收敛于某一固定值。相比之下，NLMS算法可以成功提取出有用信号，收敛速度很快，300次迭代后的输出信号与原始输入的MSK信号几乎毫无差别，均方误差的收敛性尤其出色，800次迭代后开始趋于0。这反映出NLMS 算法由于采用了变步长，自适应过程中随着输入信号的变化而控制步长，加快了收敛速度，降低了失调系数。

图6 LMS算法的噪声抵消效果

4 结语

1）由LMS算法的原理可知，影响其性能的因素主要有自适应步长和输入信号自相关矩阵的迹。自适应时间反比于步长，失调系数与步长成正比［3～7］。当参考输入信号确定时，其自相关矩阵的特征值就与滤波器的实现阶数有关。滤波器阶数越多，其自相关矩阵的迹就越大，失调系数越高，而权向量数目的增多也延缓了其平均收敛速度，使得自适应学习过程变长。所以当别的参数固定不变时，增大滤波器的阶数会造成滤波器性能的恶化。上面的仿真实验也充分说明了这一点。

2）当待抵消的噪声为白噪声时，LMS 和NLMS算法的滤波效果可能旗鼓相当，但是当输入噪声为有色噪声，且功率很大时，NLMS算法的优势很明显，LMS算法则存在梯度噪声被放大，失真度高的问题。

3）为使自适应噪声抵消系统性能达到最佳，选取合适的参考输入信号是关键，要求其与原始输入中的噪声有较大相关性，而与有用信号完全不相关。

［1］田玉静，左红伟．自适应噪声抵消的应用研究［J］．青岛建筑工程学院学报，2005，26（1）：77-80．

［2］邱天爽，魏东兴，唐洪，等．通信中的自适应信号处理［M］．北京：电子工业出版社，2005：1-47，156-162．

［3］龚耀寰．自适应滤波（第二版）—时域自适应滤波和智能天线［M］．北京：电子工业出版社，2003：89-133．

［4］曹斌芳．自适应噪声抵消技术的研究［D］．长沙：湖南大学，2007：30-34．

［5］何振亚．自适应信号处理［M］．北京：科学出版社，2002：15-23．

［6］赵春晖．自适应信号处理［M］．哈尔滨：哈尔滨工程大学出版社，2006：60-85．

［7］杨红，李德敏，林苍松，等．一种新的变步长LMS自适应滤波算法［J］．通信技术，2010，43（11）：153-156．

［8］田玉静，左红伟，朱周华．LMS与RLS算法仿真消噪对比研究［J］．通信技术，2009，42（12）：161-163．

［9］吴怡．基于LMS算法的语音增强系统的研究［D］．北京：北京邮电大学，2011：21-23．

［10］袁鹏飞．基于DSP 的自适应噪声抵消技术的研究［D］．成都：西华大学，2011：24-26．