基于信息融合技术的多阶段可靠性评估方法研究＊

2014-11-23

舰船电子工程 2014年2期

（海军航空工程学院飞行器工程系烟台 264001）

1 引言

信息融合技术是现代信息技术和多学科交叉、综合、延拓产生的新的系统科学，随着计算机科学、网络及通讯技术，微电子技术和控制技术的飞速发展，它也得到了迅猛的发展。尤其是近些年来，它的理论和方法已被应用到许多其他的研究领域。其中最早体现其优越性的是在20世纪70年代末期，军方将这种技术成功应用到了C4I和IW 系统中［1］。后来，随着信息时代的到来，尤其是20世纪90年代之后，信息融合技术在军事领域里的应用更加深入和广泛［2］。特别是在许多小子样评估问题中，信息融合技术的引入为评估方法提出了一条新的研究思路［3］。即对于存在多个数据来源的系统、设备和部件，综合利用多种可靠性数据，可以更精确地确定其可靠性水平［4］。因为对于许多由不同单元组成的复杂军事产品来说，例如导弹，一方面，由于导弹造价高昂，人力、资金、时间都受到限制，系统可靠性试验数量很少，甚至没有条件进行系统试验，企图通过大量现场试验获得可靠性数据极为不现实［5］；另一方面，在导弹设计、制造、试验和使用等过程中产生了大量的可靠性信息，甚至是相似导弹的可靠性信息也是可用的。所以在导弹可靠性评估问题上，基于导弹可靠性数据自身的特点，将信息融合技术引入可靠性数据分析领域进行可靠性数据的利用，一方面可以更精确地确定其可靠性水平，提高数据的可信性，降低模糊不确定性；另一方面这也是降低导弹研制成本、节约社会资源的重要手段。

2 导弹可靠性信息的特点与信息融合技术的应用结合

首先，在以往的导弹可靠性评估过程当中，所采用的数据主要为导弹可靠性试验的结果［6］。但是这种数据十分稀缺，有时并不能充分反映导弹的可靠性水平。信息融合技术可以扩大系统处理信息的空间包含范围，可以从多个不同的来源、环境、层次以及不同分辨率来观察同一个对象。这样多信息源的观察方法可以更充分地得到与对象相关的信息。在这种情况下，收集到的专家可靠性意见、分系统可靠性评估数据、相关（相似）系统可靠性数据以及不同场景下的可靠性数据等信息，都可以通过采用信息融合技术中提供的丰富的定性-定量融合方法（如专家系统、模糊集理论）得出可信结论［7］。这种方法有效地综合了多源信息，使得可靠性评估结果的可信度比起单纯的依靠可靠性试验结果来说要高许多。

其次，在导弹可靠性信息的收集过程中，还可以利用信息融合算法强大的时间延展能力。因为导弹从最初研究、设计、定型到后来投入生产并交付军方使用的整个过程中，产生了大量的数据。以时间为划分依据可以分为设计阶段数据、制造阶段数据、试验阶段数据和使用阶段数据［8］。它们为导弹改进工作提供了依据，有助于分析和更全面地了解导弹及其性能，最重要的是通过收集整理相关数据，可以对导弹可靠性进行预测和评估。而信息融合技术可以利用不同时间点的信息进行优化处理。亦即综合利用同一导弹寿命周期中导弹设计、制造、试验、使用和维护等各阶段的可靠性信息，配准历史数据与当时试验数据，使用合理的融合结构和算法，达到去除冗余、克服歧义的目的，得到优化的一致性准确判别［9］。这一优势与导弹可靠性数据的自身特点不谋而合。

从上述两个方面可以看出，研究以信息融合技术为基础的可靠性评估方法，可以充分利用各种时空条件下的多种信息，将这些零散的数据进行关联、处理和综合。可以得到导弹更完整、更准确的判断信息。为进一步可靠性预测或评估打下坚实的基础。下文则尝试针对导弹可靠性数据在获取过程中存在的阶段性特点，提出以信息融合技术为基础，分阶段综合可靠性信息的方法，并就其实现形式和途径加以探讨。

3 导弹多阶段可靠性数据融合模型

上述理论分析已经基本上证实了将信息融合技术应用在导弹可靠性评估问题中的可行性。在上述思想的基础上，选取信息融合算法中的Bayes方法为基本评估方法，按照同一导弹不同时期信息为思路可以建立以下的基本假设［10］：

1）在导弹研制的各个阶段中，导弹的试验环境没有发生大的变化。

2）在各阶段的试验结束后，都对导弹采取了改进措施。因而，后一阶段导弹的可靠性要高于第一阶段。

3）寿命服从指数分布，即导弹寿命的密度函数为

其中，λk为导弹在第k阶段的失效率。

4）相邻阶段间导弹可靠性的变化可以通过可靠性变化因子η联系起来［11］。

依据Bayes相继律的基本思想，通过将前一阶段的后验分布转换为后一阶段的先验分布，可以实现序化的多阶段可靠性数据的融合分析。由于Gamma分布适应性较好（通过改变两个分布参数可以以较高的精度接近其他分布），且是指数分布均值倒数的共轭先验分布。因此，选取Gamma分布作为第k阶段分布中参数k的先验分布。即第k阶段中，k的先验分布为

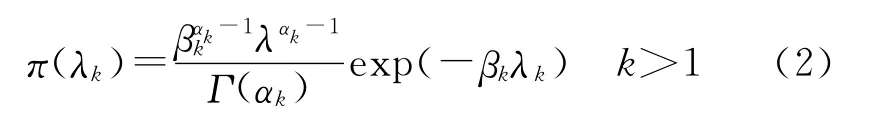
其中，λk，αk，βk＞0。

在第一阶段，如果没有其他先验信息，则选取无信息先验分布，即

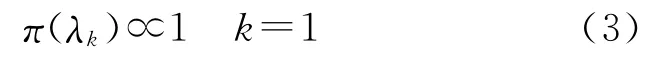
此时的先验分布可以看作是Gamma分布中α1＝0，β1＝0的情况。

后验分布为

然而一般来说，在阶段性试验之后都会对导弹进行质量改进，使得导弹可靠性得到大幅度提高。因此，如果直接使用上一阶段的后验分布作为下一阶段的先验分布，是不合适的。这时考虑引入可靠性变化因子来弥补这个缺陷。

假设第k-1阶段和第k阶段间的可靠性变化关系满足

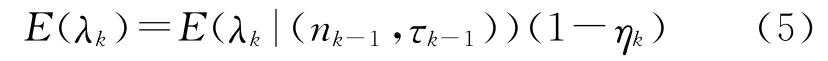
其中表示阶段间的可靠性变化因子，0＜ηk＜1。τk-1表示第k-1阶段的累积试验时间，nk-1表示累积失效次数。

因此

为了建立求解αk和的方程关系，假设阶段末的改进未影响上一阶段验后分布的方差。于是有

由式（6）～式（7）得

因此，将上一阶段后验分布转换为下一阶段先验分布的关键就是选取可靠性变化因子ηk。能否合理准确地选择变化因子则是可靠性评估精确度高低的直接影响因素。

4 可靠性变化因子的选取

1）经典统计方法

在第k阶段和k-1阶段分别求出失效率的估计值和。因为两阶段的估计值满足＝（1-ηk）。所以可以得到两阶段之间的变化因子公式为

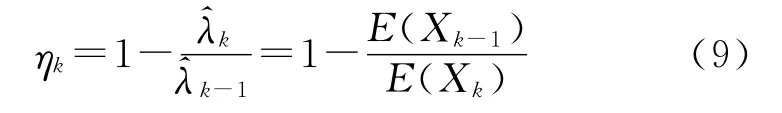
2）F分位点估计

由文献知，对于寿命服从指数分布的定时截尾试验，有

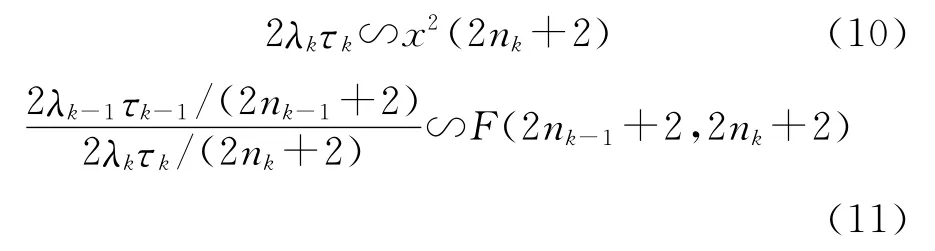
选定显著性水平γ，因而

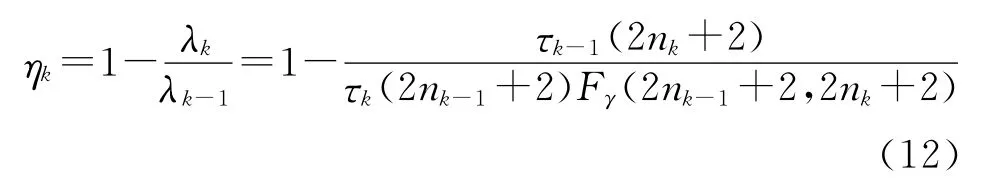
3）ML-Ⅱ方法

设第k阶段的试验信息为（nk，τk），根据第二类极大似然估计的思想，它为其边缘密度m（t）所产生的子样

结合式（2）有

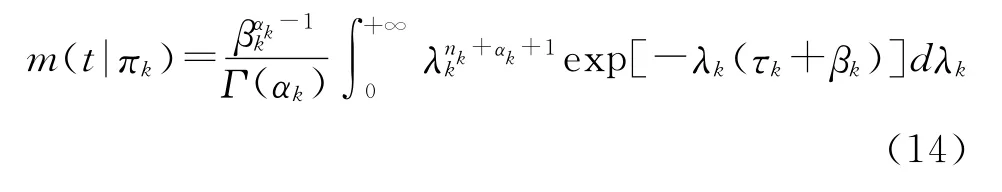
由Gamma函数的积分特性

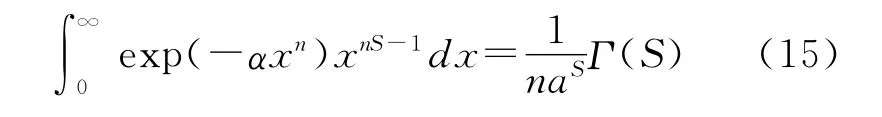
简化上式得

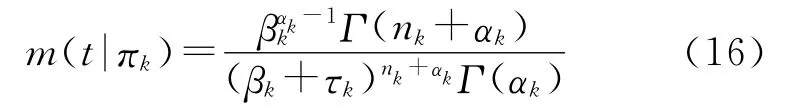
为求取ηk，将式（8）代入（16），则m（t｜πk）就只含有一个未知参数。令则有

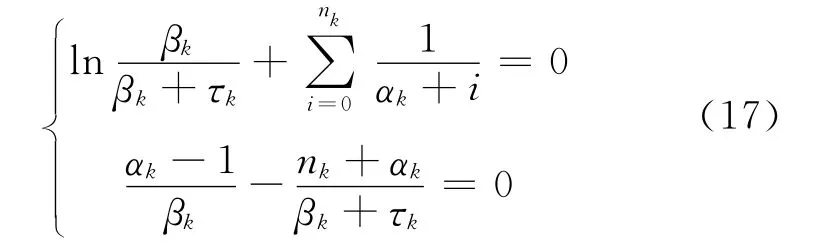
采用数值迭代的方法即可求出αk和βk。

5 实例分析

假设某型导弹的研制已经经历了三个阶段，试验数据如表1所示。可以通过本文中的推断方法对该型导弹进行可靠度评估。大体推断过程如下：

表1 某型导弹三阶段试验数据

导弹在这三个阶段内的寿命均值和方差分别为

第一阶段：E（X1）＝79．83，Var（X1）＝3089

第二阶段：E（X2）＝353．89，Var（X2）＝1398

第三阶段：E（X3）＝775．86，Var（X3）＝12570

因为Gamma分布的性质可以表示为E（Xk）＝由此可以得到三个阶段的估计值分别为通过本文提出的三种方法，对每两个阶段的可靠性变化因子进行估计，得到的估计值如表2所示。

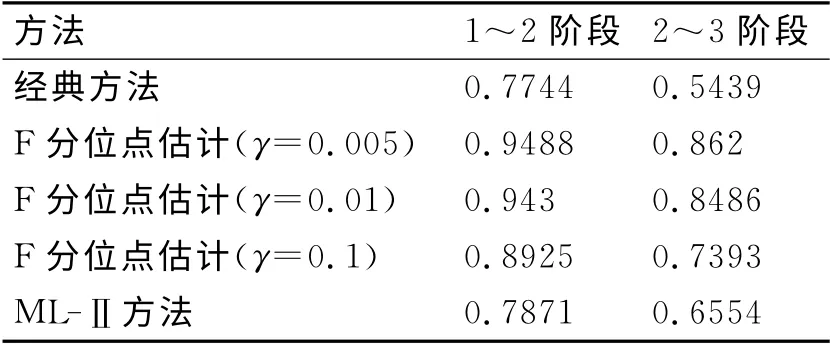
表2 三种方法对继承因子各阶段间的估计情况

由案例可以看出，各种方法都有其突出的方面。经典方法计算过程简便快捷易于操作；F 分布点估计方法得到的结果受置信水平影响较大；ML-Ⅱ方法由于考虑到了样本信息和前一阶段的信息，计算结果的可靠性则更高一些。最后结合经典的可靠性评估方法对导弹进行可靠性评估，可以发现，融入变化因子的可靠性评估方法具有更高的可信度，其得到的评估值更加精确。