RLS算法理论分析及研究＊

（海装装备采购中心 北京 100097）

1 引言

RLS（Recursive Least Square）算法，即递推最小二乘法，在信号处理领域有广泛的运用。此算法具有优异的未知参数跟踪能力和快速的收敛性能。图1是最小二乘算法（Least Square，LS）的 原理图，w［n］表示在第n时刻的权向量。假设在第n时刻，已经输入n＋1组信号x［0］，x［1］，…，x［n］，同时输入n＋1个比较信号d［0］，d［1］，…，d［n］，那么输出n＋1个误差信号是［1］：

图1 LS算法原理图

令

2 LS数学模型

这里，0＜λ≤1，称作遗忘因子（减少旧数据的影响）。为了求出最优权向量wopt，引入如下M×（n＋1）矩阵（M表示阵元数目）

和对角矩阵

那么

根据

得到

3 RLS算法

从wopt的表达式可以看出，如果直接计算wopt，不仅涉及到矩阵求逆，还随着时间的推移，各种矩阵的维数变得越来越大，最终导致计算量的急剧增加。针对这个问题，提出一种递推的计算方法就十分合理了。递推最小二乘算法（RLS）正是针对上述缺点提出的计算方法［3］。

基于RTDS与QualNet的电网和通信网半实物联合仿真系统//童和钦,倪明,李满礼,司庆华,缪源诚,龚鹏//(8):149

为了方便叙述，令

那么

那么根据矩阵求逆引理，

经过计算推导，RLS算法公式如下述：

4 RLS算法收敛性质

4．1 线性回归模型

设（Ω，F，P）是基本概率空间，F是事件域，P是概率测度。术语“Ω上的随机变量X”是指X：Ω→｛所有实数｝是Ω上的可测函数，即每个Borel集B的原像集X-1（B）∈F；术语“离散时间随机过程”就是由整数指定的随机变量序列｛Xn｝。当用随机变量来描述随机信号时，指标n通常是指时间［4］。

设Yn和υn是随机过程（注意υn是零均值的随机过程，即E（υn）＝0），Xn是随机过程向量，比如

如果存在常系数w1，…，wM，使得

那么这样的数学模型就称作线性回归模型（Linear Regression Model），常系数w1，…，wM就称作回归系数，υn称作误差过程。通常假定是白噪声过程。如果令

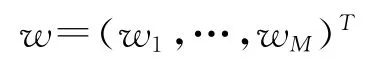
那么线性回归模型就可以用向量表示，即

4．2 滤波器系统模型

假定图2的滤波器系统比较信号d［n］和输入信号x［n］满足线性回归模型

式（12）中，eo［n］是误差随机过程，是白噪声，即［5］：

令

那么

所以

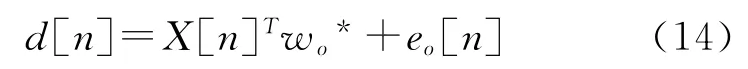
4．3 无偏估计

根据LS 算法数学模型，wopt［n］是随机过程。针对随机过程wopt［n］，通常首先考察它的期望E（wopt［n］）。注意到［6］：

那么

所以wopt［n］是wo的无偏估计（Unbiased Estimation）。

4．4 自协方差矩阵

由于wopt［n］是随机过程，那么不仅要保证它的期望是无偏估计，还要考察它在期望附近的波动情况，即要考察它的自协方差矩阵。为了研究自协方差矩阵，首先令［7］：

那么自协方差矩阵

那么

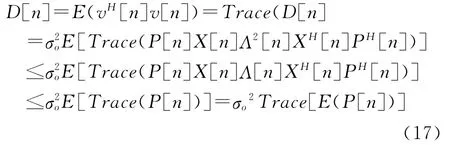
为了估计Trace（P［n］），假定输入信号x［n］是各态历经的平稳信号，那么可以证明当n足够大的时候

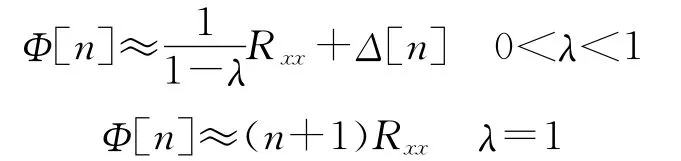
这里，Rxx是输入信号自相关矩阵，即［8］：

Δ［n］是零均值的Hermite可逆矩阵，即：

那么

可以得到

这里‖A‖表示矩阵A的某种范数。那么成立

所以相关矩阵的最小特征值越大，收敛性越好，并且λ越接近1，收敛性越好。

5 RLS算法仿真

图2 不同Lamda值对比图

利用RLS-Systolic模型来进行抗干扰仿真。分别对λ＝0．9、1、0．99三种情况进行仿真，仿真天线阵元数目M＝4，干扰数目L＝2。图2为仿真对比图［9］。

从图2可以看出，Lamda越接近1，收敛情况越好，表现出干扰抑制深度越好。

图3是RLS和LMS收敛速度对比图，从图中可以看出RLS收敛速度要比LMS收敛速度快很多。

图3 RLS和LMS收敛速度对比图

6 结语

综上所述，RLS算法具有优异的未知参数跟踪能力和快速的收敛性能。通过对RLS算法研究方法的进一步汇总，以及更深入的数学探讨，提出了相应性质的估计。这些性质估计表达式揭示了RLS算法的特性，可用来指导工程实践［10］。

［1］李飞，黄涛，刘永飘，等．基于QRD-RLS的数字预失真算法的研究［J］．光通信研究，2011，37（2）：64-66．

［2］Haykin S．自适应滤波器原理［M］．郑宝玉，等译．北京：电子工业出版社，2006．

［3］Manolakis D G．统计与自适应信号处理［M］．周正，译．北京：电子工业出版社，2002．

［4］张庆华，樊振方．基于RLS算法实现激光陀螺抖动信号剥除［J］．激光技术，2010，34（5）：673-675．

［5］曹华，刘建业，祝燕华，等．光纤陀螺组件误差标定ARLS算法［J］．光电工程，2008，35（6）：48-53．

［6］熊智，刘建业，林雪原，等．激光陀螺捷联惯性导航系统中惯性器件误差补偿技术［J］．上海交通大学学报，2003，37（11）：1795-1799．

［7］范胜林，孙永荣，袁信．捷联系统陀螺静态漂移参数标定［J］．中国惯性技术学报，2000，8（1）：42-46．

［8］王海．光纤陀螺温度影响与误差补偿［J］．北京航空航天大学学报，2007，33（5）：549-551．

［9］郭创，张宗麟，王金林，等．激光陀螺温度特征点选择及其补偿［J］．光电工程，2006，33（6）：130-134．

［10］陈凯亚，王敏锡．二阶伏特拉滤波器RLS 算法改进［J］．电子科技大学学报，2005，34（4）：467-469．