基于蒙特卡洛模拟的电压稳定评估方法

方延洪

（重庆大学 数学与统计学院，重庆 400030）

电力系统是一个复杂的大规模非线性动态系统，有关其稳定性与控制方面的研究一直是电力系统规划与运行的重要课题.长期以来，电力系统的功角稳定问题一直受到人们的关注；而电压的稳定作为电力系统稳定性的另一个重要方面，直到20 世纪80年代才引起了国际电工学界的广泛关注.

概率潮流方法在 20 世纪 70年代由B.Borkwaska［1］提出，目前国内外已经提出的概率潮流算法主要有：一次二阶矩法［2］，点估计法［3-4］等.文献［5］提出利用Gram-Charlier级数或半不变量法替代原先的离散卷积，经过这样的处理，运算速度得到了提升，同时数值计算的稳定性也得到了保证，但与此同时节点注入功率的相关性却很难处理［6］.

模拟法不要求对系统进行精确建模，虽然计算较为复杂，但却可以很好地处理随机性问题.蒙特卡洛方法［7-8］属于比较典型的模拟法，可较为准确地获得状态电压和支路潮流的概率描述.拉丁超立方采样方法可以有效地提升计算效率，在支路潮流越限的分析中已经得到了应用［9］.节点参与因子是被广泛接受的电压稳定指标［10］，但是一般参与因子数值较小，不利于分析也不直观，在实际中需要一个能直观反映各个节点电压变化的指标来指导电力系统的运行.

本文利用拉丁超立方采样进行了概率潮流计算，分析了节点电压的概率分布，为评估节点电压的稳定性，提出了节点电压越限概率指标，在IEEE118节点和某实际大系统上进行了计算分析，结果证明了方法的有效性.

1 随机计算模型

1.1 负荷随机分布模型

一般来说，发、输、配、用各个部分的模型和参数都是潮流计算的组成部分，但负荷模型的选择对电网静态安全分析影响很大.在一些情况下，计算分析的结果可能由于负荷模型选择的不同而出现很大的差异，因此应当选择合适的负荷模型，以提高计算分析的准确度.负荷模型假设：每个母线k的负载保持恒定的功率因数，换言之，即在母线k的无功消耗是与有功成正比的，这取决于功率因数恒定的比例ak.

式中：Qdk为母线k上的无功功率消耗；Pdk为母线k上的有功功耗；ak为比例常数.

更具体地说，如果母线k上的负载有一个功率因数pfk，那么ak＝tan（cos-1（pfk））.因此，Qdk是取决于vi的线性的相关随机变量.

1.2 发电机出力调度模式

实际发电机出力有上限，当出力越限时必须设置相应的判断语句进行处理.本文的处理方式为：如果发电机有功出力越限，则将其有功出力固定在额定值；如果节点无功越限，则转换为PQ节点，平衡节点转化为PQ节点后，在其附近挑选一台发电机作为平衡机以平衡网损.具体流程如图1 所示.

图1 发电机出力调度流程图Fig.1 Flow chart of generator output dispatch

1.3 拉丁超立方采样

拉丁超立方采样是一种分层采样技术，由M.D.Mckay 在1979年提出［11］，其主要特点如下：①对输入变量的每个概率区间进行抽样，确保抽样覆盖整个分布区域；②利用正交化算法消除采样点之间的相关性，可以最大限度地保留基本信息，分为以下两个步骤.

1.3.1 采样

设L1，L2，…，Lk是k个随机输入变量，其累计概率分布为

其采样示意图如图2 所示.

图2 拉丁超立方采样示意图Fig.2 Schematic diagram of Latin hypercube sampling

首先根据采样次数将累计概率曲线分为N份，然后利用公式（3）反演采样数据

采样后得到采样值矩阵，每一行代表一个随机变量的采样值，当采样N次时，采样矩阵是一个K×N的矩阵.

1.3.2 排列

形成采样矩阵之后，矩阵元素之间有可能还有一定的相关性，这使得采样的信息量没有达到最优，拉丁超立方采样利用正交化算法减小了采样数据之间的相关性，相应流程如图3 所示.

图3 排列流程图Fig.3 Flow chart of Ranking

图3 中，Lk←takeout（Lk，Lj）表示将Lk，Lj线性回归分析中的残差赋值给Lk，经过这样处理之后，采样矩阵元素间相关性会较小.

1.3.3 拉丁超立方采样的优点

拉丁超立方采样可以均匀地覆盖整个采样区间，而且正交化算法可以确保采样得到的信息量得到最大优化.图4 和图5 分别是采用二维正态拉丁超立方和普通随机采样得到的样点图.

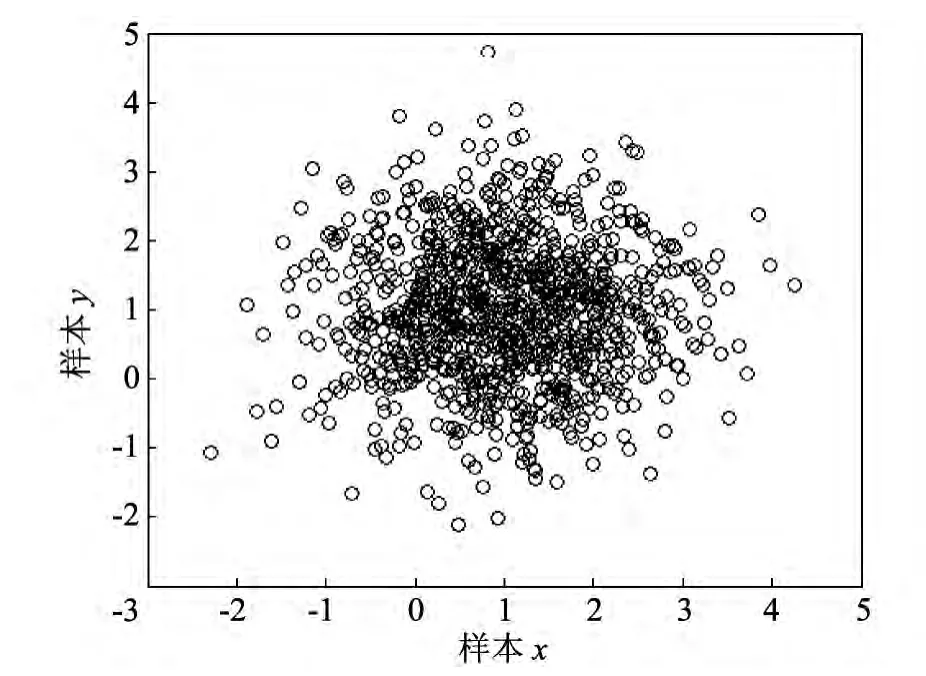
图4 二维拉丁超立方采样图Fig.4 Latin hypercube sampling graph in two dimension

对比图4 和图5 可以较为清楚地发现拉丁超立方采样得到的图形更加集中，对正态分布的信息体现的更好.

图5 二维简单随机采样图Fig.5 Normal sampling graph in two dimension

1.4 随机潮流计算流程

为了考虑负荷的波动性，利用1.3中的拉丁超立方采样生成随机干扰矩阵，叠加基态负荷后，发电机出力按照1.2中规则相应地变化，在修正功率后重复进行确定潮流计算若干次.本文重点研究的是概率潮流计算，所以假设各个负荷节点有功的变化是相互独立的.设重复50 000 次计算的结果是准确的，计算出的节点电压期望和标准差分别为μaccurate和σaccurate，用μsimulated和σsimulated表示在较少采样次数下输出的随机变量期望值与方差.定义期望相对误差和标准差相对误差为

计算流程如图6 所示.

图6 随机潮流计算流程图Fig.6 Flow chart of stochastic power flow calculation

1.5 节点负荷参与因子

节点负荷参与因子是模态分析中一个重要的指标［10］，是指在全网负荷增长的情况下，按节分岔点系统各个节点对失稳的贡献，表示为电压对无功的偏导.

根据潮流方程

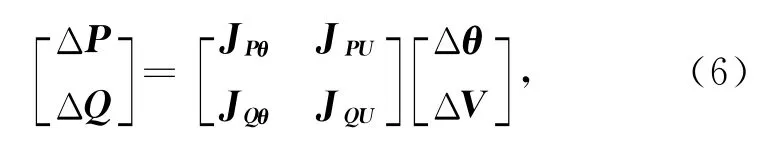
式中：ΔP为节点注入有功功率的变化量；ΔQ为无功变化量；Δθ是相角修正量；ΔV是节点电压修正量；J代表潮流雅克比矩阵.

令ΔP≡0，得到

式中：JR＝JQU-JQθJ-1PθJPU为线性化雅克比矩阵，对其进行奇异值分解，

在此基础上，节点参与因子定义为

表征在节点k处，第i个特征根对电压灵敏度的贡献，节点参与因子越大，表明该节点电压稳定的裕度越小，需要采取措施提高电压的稳定性.

2 算例分析

2.1 IEEE118 系统

作为一种统计方法，蒙特卡洛模拟的收敛过程通常具有波动性，且随着系统的变化、算法的不同而差异很大.本文通过多次采样进行潮流计算，以减小随机波动性的影响，分别利用普通采样和拉丁超立方采样产生随机负荷，利用概率潮流模型对IEEE118 系统计算1 000 次，2 000 次，5 000次，50 000次，以50 000次计算作为标准结果，各次计算的误差如表1 所示.

从表1 中数据可得，利用拉丁超立方采样的模拟方法，在2 000 次左右的时候就可以达到简单采样5 000次时的精度，在计算5 000次后，拉丁超立方得到的结果要优于简单采样的结果.拉丁超立方采样1 000 次和简单采样5 000 次的结果与标准采样结果的比较如图7，图8 所示.

表1 IEEE118 系统两种采样方法的误差Tab.1 Error comparisons between two methods on variable sampling methods for IEEE 119-bus system

图7 拉丁超立方采样结果比较图Fig.7 Result of Latin hypercube sampling

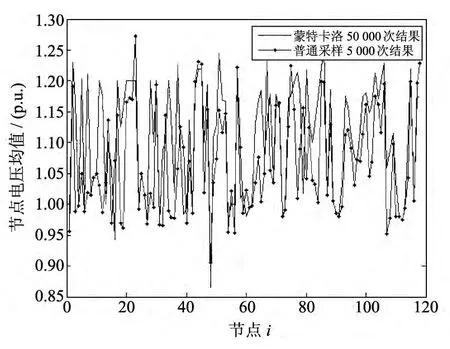
图8 简单随机采样结果比较图Fig.8 Result of normal sampling

2.2 电压越限概率和连续潮流节点参与因子的相关性分析

在电力系统运行中，由于负荷的波动性，节点电压会一直处于变动之中，如果电压的变化不可控制，在运行中通常认为电压失去了稳定.本文以电压高于1.1，低于0.95为电压越限，利用概率潮流计算得到的电压越限概率指标来衡量系统电压的稳定性风险，即越限概率越大，系统的电压越会长期偏离正常值，这时候需要采取相应的措施来保证电压的稳定性.

作为一种数值延拓法，连续潮流是静态电压稳定最成熟的分析工具，本文在全网负荷增长的情况下，利用连续潮流计算出了系统失稳时各个节点对失稳的贡献，并分析了这一指标与电压越限概率之间的相关性，证明了本文提出指标的有效性.因一般节点参与因子数值较小，故图9 中的节点参与因子都乘以了同一系统，以保证越限概率.

图9 IEEE118 系统节点电压越限概率相关性分析Fig.9 Correlation analysis of node voltage out-of-limit probability on IEEE 118-bus

从图9 中可以看出，电压越限概率指标与节点参与因子具有一定的相关性，大部分的节点的电压越限概率与节点处参与因子呈正相关，在86节点和95节点处具有较高的越限概率，而这几个节点的参与因子也处于峰值，可见电压越限概率确实对衡量静态电压稳定性具有一定的作用.

2.3 电压越限概率在2012年某省电网中的应用

某省2012年的电网共有2 569 个节点，是典型的复杂大系统.应用本方法后，随机挑选了97个节点，其电压越限概率和节点电压参与因子如图10 所示.

由图10 中数据计算得出，本文提出的越限概率指标与节点参与因子间的相关系数为0.396 3，具有较为明显的相关性，在节点电压越限概率较高的地方，节点的参与因子也比较大，表明此节点在运行状况下距离失稳点比较近，应当采取措施降低该节点的运行风险.而且本文提出的指标比节点参与因子更加直观，清楚地表示了节点电压的变化情况，相比于节点参与因子更加实用.

图10 某省电网节点电压越限概率相关性分析Fig.10 Correlation analysis of node voltage out-of-limit probability on a province grid

3 结论

本文提出了一种基于蒙特卡洛模拟的电网电压稳定评估方法，越限概率可以用来评估电网各个节点在负荷波动情况下的电压稳定性.若越限概率偏大，则必须采取相应的措施来提高该节点的电压稳定性.

1）拉丁超立方采样下，2 000 次随机潮流计算的收敛结果与普通采样方法5 000 次的结果接近，说明在采用拉丁超立方采样后计算时间大大减小，方法的快速性得到了提高.

2）在本文的随机潮流计算中，方差的相对误差更小，说明节点电压方差的收敛程度优于节点电压的期望值，利用蒙特卡洛模拟节点电压的方差值更加有效.

3）在蒙特卡洛模拟计算中，由于需要计算节点电压的期望和方差，对于每一步潮流计算所得的结果都必须保存，相比于普通采样，拉丁超立方采样在采样次数较少的情况下可以得到较高的精度，所以拉丁超立方采样下的蒙特卡洛模拟对存储空间的要求更少，而且拉丁超立方采样的适用范围要优于普通采样.

4）本文提出的节点电压越限概率指标和连续潮流节点参与因子具有一定的相关性，这说明节点电压越限概率可以作为评估节点电压稳定性的指标.

5）在某省2012 的网络中应用了本方法，其计算结果与节点参与因子符合得较好，证明节点电压越限概率可以较好地指示运行点的裕度，其作为一种指标可以应用于大系统电网的静态安全评估中.

［1］Borkowska B.Probabilistic load flow［J］.IEEE Trans on Power Apparatus and Systems，1974，93（3）：752-759.

［2］Madrigal M，Ponnambalam K，Quintana V H.Probabilistic optimal power flow［C］.Waterloo，Canada：IEEE Canadian Conference on Electrical and Computer Engineering，1998.

［3］Su C L，Lu C N.Two-point estimate method for quantifying transfer capability uncertainty［J］.IEEE Trans on Power System，2005，20（2）：573-579.

［4］Su C L.Probabilistic load flow computation using point estimate method［J］.IEEE Trans on Power Systems，2005，20（4）：1843-1851.

［5］Morales J M，Perez Ruiz J.Point estimate schemes to solve the probabilistic power flow［J］.IEEE Trans on Power Systems，2007，22（4）：1594-1601.

［6］Lei Dong.Probabilistic Load flow analysis for power system containing wind farms［J］.IEEE Transactions on Power System，2010，20（2）：1-4.

［7］段玉兵.基于蒙特卡洛模拟的微电网随机潮流计算方法［J］.电工技术学报，2011，26（增刊1）：274-278.Duan Yubing.Probabilistic power flow calculation in microgrid based on Monte-Carlo simulation［J］.Trans-actions of China Electrotechnical Society，2011，26（Sup.1）：274-278.（in Chinese）

［8］马瑞，袁文伟.基于蒙特卡洛随机选线最优潮流的电压崩溃临界点算法［J］.电力系统保护与控制，2011，39（2）：65-69.Ma Rui，Yuan Wenwei.An approach for determining voltage collapse critical point based on Monte Carlo stochastic line selection optimal power flow［J］.Power System Protection and Control，2011，39（2）：65-69.（in Chinese）

［9］于晗，钟志勇，黄杰波，等.采用拉丁超立方采样的电力系统概率潮流计算方法［J］.电力系统自动化，2009，33（21）：32-35，81.Yu Han，Zhong Zhiyong，Huang Jiebo，et al.A probabilistic load flow calculation method with Latin hypercube sampling［J］.Automation of Electric Power Systems，2009，33（21）：32-35，81.（in Chinese）

［10］Gao B，Morison G K，Kundur P.Voltage stability evaluation using modal analysis［J］.IEEE Transactions on Power Systems，1992，7（4）：1529-1542.

［11］Mckay M D，Beckman R J，Conover W J.Acomparison of three methods for selecting values of inputvariables in the analysis of output from a computer code［J］.Technometrics，1979，21（2）：239-245.