基于物理学的改善粒子图像测速稳健光流方法研究

郑 佳， 王洪雁， 裴炳南

(大连大学辽宁省北斗高精度位置服务技术工程实验室，辽宁 大连 116622)

0 引言

流体力学及空气动力学研究中流体速度场测量对于了解复杂流体具有重大意义。流体运动是一种典型的非刚性运动，其计算须基于图像处理技术。可通过对运动图像序列分析获得局部流体运动矢量大小、方向及分布情况，进而获取诸如粘性及涡流场分布等物理特性[1]。通常情况下，由于运动物体透明或不易通过光学设备观测，需将可见粒子置入被测物，以通过估计粒子运动矢量间接获得流体运动特征，此即谓粒子图像测速[2](Particle Image Velocimetry，PIV)。

常见光流计算方法，如变分光流方法的分辨率可达到亚像素级，同时，假设流体连续时空变化特性与光流方程中图像序列局部时空可微本质相同，因而，基于光流的PIV得到了广泛的关注。

马鹏飞等提出基于Lucsa-Kanade(LK)局部光流的PIV估计方法[3]，此算法计算复杂度低，稳健性较好，然而光流场边界较为模糊，边缘像素点光流估计较差，从而所得光流场较为稀疏；针对此问题，孙立志等提出基于金字塔LK的多尺度光流算法以计算PIV[4]，所提算法可解决在运动目标速度过大、相邻帧连续性不强时的光流计算问题，所得光流精度高于LK算法，然而得到的光流场仍较为稀疏；为此，黄湛等提出基于Horn-Schunck(HS)的PIV计算方法[5]，此算法可得稠密光流场，然而边界容易模糊，计算复杂度高，且稳健性较差；为进一步改善光流估计精度，余学敏等使用全局与局部结合的方法，获得了更高的光流估计精度[6]，然而此方法所得光流在边缘地区稳健性较差；为改善光流估计稳健性，文献[7]在局部与全局结合的基础上加入各向异性滤波器以减少边缘光流扩散，但是此方法对噪声及异常点的稳健性较差；文献[8]在全局与局部结合的基础上加入惩罚项，以增强对噪声和异常点的稳健性；文献[9]基于物理学的光流方法从可视化图像获取高分辨速度场，然而由于边缘区域光流扩散及噪声和异常点的影响，光流稳健性较差。针对上述问题，本文提出一种基于物理学的稳健光流计算方法以改善光流计算稳健性。在基于物理学的光流方法中引入各向异性滤波器以增强边缘光流的稳健性，增加惩罚因子以减少噪声及异常点对光流计算的影响，而后基于变分方法极小化光流能量函数以求解欧拉-拉格朗日方程，最后通过迭代方法求得速度场。

1 经典光流法

1.1 光流约束方程

在相邻图像时间间隔和图像灰度变化均很小的假设下，HORN等提出如下灰度光流计算思想：物体运动会引起与之对应像素亮度连续变化，从而形成连续变化光流场[5]，其数学模型如下。

设图像中一点(x，y)在t时刻的亮度为I(x，y，t)，在Δt时刻亮度为I(x+Δx,y+Δy,t+Δt)，当Δt无穷小时可认为亮度不变，则可得

I(x,y,t)=I(x+Δx,y+Δy,t+Δt)

(1)

对上式泰勒级数展开，当Δt→0可得

(2)

Ixu+Iyv+It=0

(3)

式中，u，v表示速度矢量的二维分量。由此可得光流计算基本等式。需要注意的是，式(3)中有两个未知参数，因而此问题无法求解。为获取两个速度场参数的估计，HORN等提出了基于全局约束的方法，而KANADE等则提出基于局部约束的方法。

1.2 Lucas-Kanade光流法

此方法核心思想如下：假设像素a与相邻区域内所有像素光流矢量相同，对区域内像素赋予不同权重，则光流计算可等价为最小化如下能量函数[10]，即

(4)

式中：Ω表示以a点为中心的小区域；▽表示梯度算子；W(x)为窗函数，表示区域中像素mi(i=1，2，…，n)的权重，离a点越近，权重越高。上式可等价为如下最小二乘形式，即

A2W2Ap=ATW2b

(5)

式中，

(6)

diag(·)为对角阵。由式(5)可得

p=(ATW2A)-1ATW2b。

(7)

LK方法可得到稀疏光流场，相对于下述HS算法，计算复杂度低，然而稳健性较差[3]。

1.3 Horn-Schunck光流法

HORN等提出的约束条件则是极小化平滑约束项[11]Es，即

(8)

而基于光流基本等式可得光流误差Ec为

Ec=(Ixu+Iyv+It)2dxdy。

(9)

基于上述两个约束条件可知，光流矢量可通过如下最小化问题获得，即

E={(Ixu+Iyv+It)2+λ(‖▽u‖2+‖▽v‖2)}dxdy

(10)

此问题可通过基于梯度的方法进行求解，从而降低计算复杂度，且可得到高精度像素瞬时位置速度及稠密光流，然而，此方法分辨率较低，边缘光流易扩散，且稳健性较差[5]。

2 基于物理的光流法

针对上述算法分辨率较低的问题，文献[9]提出一种基于物理学的高分辨率光流计算方法。此算法详细地给出了光流的物理意义，即光流与可视化图像中流体或者颗粒的速度成正比[12]。此外，在图像坐标系中，物体空间坐标系可通过透视投影变换来表述，所有这些情况下的投影运动方程可用基于物理的光流方程表述[9]为

(11)

当g▽·p=0及f=0时，基于物理学的光流方程可以简化为基于HS光流算法的亮度约束方程[9]，即

(12)

极小化式(12)可得欧拉-拉格朗日方程[9]为

(13)

式(13)可通过标准有限差分方法来进行光流求解。基于物理学的光流计算方法，可以得到较HS方法更高分辨率的光流。然而，由于基于物理光流方法光流在边缘地区易扩散，且易受噪声和异常点影响，光流整体稳健性较差[9]。

3 基于物理学的稳健光流算法

为了减少角落和边缘光流扩散对光流计算的影响，文献[7]提出各向异性扩散的光流计算方法，并给出了扩散系数方程。此方法可减少光流在边缘的传播，增强边缘光流稳健性。所提的两个扩散系数方程可表示为

(14)

(15)

其中，式(14)更适用于高对比度情况下的稳健光流求解，式(15)更适用于较宽区域的稳健光流求解[13]。

常量K控制边缘的敏感度，通常由实验确定其数值。为了能够兼顾对比度和区域大小对光流计算的影响，求得稳健性更高的光流，本文采用扩散系数方程[7]为

D(‖▽I‖)=e-α‖▽I‖β1。

(16)

基于式(16)，光流能量函数式(12)可改写为

(17)

式中，E2=‖D▽u‖2+‖D▽v‖2。

加入惩罚项，式(17)可改写为

(18)

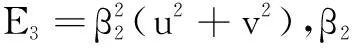
根据变分原理将E(u,v)最小化，可得欧拉-拉格朗日方程[14]为

(19)

式中：

L=L(u,v,ux,uy,vx,vy)=(E1)2+E3+λE2；

(20)

(21)

将式(20)及式(21)代入式(19)可化简为

(22)

式中，▽·(gp)=g▽·p+p·▽g，可用某点与其周围速度平均值之差近似表示，即

(23)

结合式(23)，式(18)可重新表示为

(24)

式中，E4=gt+ugx+vgy+gux+gvy-f。

对式(24)整理可得

(25)

式中，

(26)

求解式(25)得un+1和vn+1为

(27)

式中，

(28)

至此，可得基于物理的稳健光流计算方法。此方法可具体描述如下。

1) 读取连续两帧粒子图像，对其滤波以减小噪声，并初始化所需参数。

2) 使用sobel算子对滤波后图像求x方向、y方向导数；利用两帧中对应像素相减方式求t方向导数。

3) 采用九点差分格式计算u，v均值[15]。

4) 计算求解点灰度梯度，设定速度平滑权重系数(设为1)，初始速度设为0。

5) 根据式(26)，基于Gauss-Seidel方法迭代求解[16]。

6) 若相邻两次迭代光流之差小于给定阈值，或迭代次数超过给定值，则终止迭代。

4 实验仿真及分析

通过与经典HS，LK光流算法以及金字塔LK光流算法和基于物理的光流算法进行对比，验证所提基于物理的稳健算法针对所得光流密度及边缘光流扩散效果的有效性。仿真参数设置如下：各向异性滤波器相关参数α=5，β1=0.8，惩罚函数相关参数β2=0.02，迭代误差ε=1×10-3，迭代次数n=200。

(29)

式中，

(30)

实验1 图1所示为等流速状态下两帧连续的粒子图像，以下算法皆基于此计算光流。图2所示为LK光流算法、HS光流算法、基于金字塔LK光流算法以及基于物理算法得到的光流图像。由图2可知，与HS光流算法相比，LK光流算法得到的光流稀疏，稳健性较好。HS光流算法虽可得稠密光流，但稳健性差。较HS光流算法和LK光流算法，基于金字塔LK光流算法所得光流精度较高，稳健性较强，但光流较稀疏。此3种光流算法所得光流分辨率较低。基于物理光流算法可得高分辨光流，但边缘易扩散，且易受噪声和异常点影响，光流较稀疏，稳健性较差。

图1 原始图像Fig.1 Original images

图2 基于物理光流算法与经典光流算法所得光流对比

实验2 图3分别为基于物理光流算法及加入惩罚因子后基于物理光流算法所得光流图像，惩罚因子中β2=0.02。由图3可知，在基于物理光流算法基础上加入惩罚因子后对噪声和异常点的稳健性较好，但由于光流在边缘地区易扩散，所得光流较为稀疏。

图3 惩罚因子对基于物理光流算法的影响Fig.3 Effect of penalty factor on physical optical flow algorithm

实验3 图4依次是基于物理光流算法和基于物理的加入各向异性扩散后的光流算法得到的光流图像，其中，扩散系数方程参数α=5,β=0.8。由图4可得，后者可显著降低光流在边缘地区的扩散，光流较为稠密，但由于噪声和异常点影响，光流稳健性较差。

图4 各向异性扩散对基于物理光流算法的影响Fig.4 Effect of anisotropic diffusion on physical optical flow algorithm

实验4 图5是使用基于物理光流算法和基于物理的稳健光流算法得到的光流图像，其中，α=5,β1=0.8,β2=0.02。由图5可得，基于物理的稳健光流算法可明显减少边缘光流扩散，且显著降低噪声和异常点对光流计算的影响，得到较稠密光流，从而可改善光流计算的稳健性。

图5 基于物理光流算法和基于物理的稳健光流算法对比

综上所述，与LK,HS,基于金字塔LK以及基于物理光流算法相比，本文所提的引入各向异性滤波器及惩罚因子的基于物理的稳健光流算法可增强光流计算对噪声和异常点的稳健性，同时明显减少边缘地区光流扩散，进而得到稠密的光流，从而可显著改善光流计算的稳健性。

5 结束语

针对可视化流动图像边缘易扩散和噪声点及异常点的影响使得光流计算稳健性较差的问题，本文提出一种基于物理学的稳健光流算法以改善光流计算的稳健性。所提算法在基于物理光流算法中引入各向异性滤波器以增强边缘光流的稳健性，增加惩罚因子以减少噪声及异常点对光流计算的影响。而后基于变分方法极小化光流能量函数求解欧拉-拉格朗日方程，最后通过迭代方法求得速度场。仿真结果表明，与传统的LK,HS,基于金字塔LK以及基于物理光流算法相比，所提算法可显著减少边缘和角落区域的光流扩散，改善针对噪声及异常点的稳健性，从而得到具有较好稳健性的速度场。