电力系统暂态稳定性闭环控制（二）——多机电力系统暂态不稳定判别方法

张保会，杨松浩，王怀远，马世英，吴丽华

（1.西安交通大学 电气工程学院，陕西 西安 710049；2.中国电科院 电力系统研究所，北京 100192）

0 引言

实际大规模电力系统中的发电机一般会配有调速器、励磁调节器等，同时负荷是实时变化的且具有动态特性，这些因素导致了电力系统的时变性，简而言之，实际的电力系统是一个极其复杂的多机时变非自治系统。目前被认可和使用的电力系统暂态稳定性分析如等面积准则（EEAC）[1]、势能边界法（PEBS）[2]、基于轨迹凹凸性的方法[3-4]等理论也正在努力适应这种时变性，但限于目前的数学理论进展，对这种非自治因素[5]对稳定性的影响尚无法准确估计。因此，对实际多机系统进行暂态稳定性闭环控制时必须考虑非自治因素的影响，才能得到准确可靠的供实际应用的结论。

另一方面，在实际的电网中，故障的类型、持续时间、故障地点均不可预知，但是故障导致的系统暂态失稳的方式却可以总结为几种典型的形式。最常见的暂态失稳方式就是首先两群失稳，即系统中可以看到两群间功角差距非常明显，并且会越来越大，直到失稳，而后极少情况再发展为多群失稳。对于此类两群率先失稳模式，文献[1]使用了互补群惯量中心变换（CCCOI）的数学处理方法，将两群失稳方式的多机系统等值成一个单机无穷大系统，并且证明了这是一个保稳等值变换，多机系统的稳定性与等值单机系统的稳定性相同，使得利用相平面法分析多机系统成为可能。

由于多机系统中机组、负荷模型参数、调节特性、运行方式、故障类型与故障切除时间等时变因素对稳定性的影响都真实地反映在实测轨迹上，只要对运动轨迹的特性与稳定性的关系进行充分研究利用[6-12]，就考虑了以上因素对稳定性的影响。本文在本系列文章（一）[13]的基础上，发展了功角－角加速度平面刻画非自治因素对轨迹发展的影响，结合轨迹凹凸性的变化特征，判别多机系统的暂态稳定性，可以满足稳定性闭环控制所要求的快速性和准确性。

1 多机系统的分群和等值

本文主要讨论多机系统为两群率先失稳模式下暂态不稳定判别方法，首先需识别、分离失稳的两群。

文献[14]是对几种电力系统同调机群识别方法的综述，文章分析了各方法的优劣及使用场景，基本分群原则是依据当前或未来功角的相近性，将机组分为若干同调群。文献[15]通过对发电机摇摆曲线进行小波分析进而计算发电机组间的相关系数，从而实现同调机群识别。文献[16]通过构造一个考虑角速度影响预测未来一个时段后的功角进行实时分群。

大扰动后机组间的分离是暂态过程中功角发展的结果，下一个时段的功角与本时段的功角、角速度及加速度（不平衡功率）有关，为了使得依据下一个时段的功角分群准确而又计算简单，构造下一个时段功角预测，其形式如下：

其中，δi（t）、ωi（t）、ΔPi（t）分别为 t时刻第 i台发电机的功角、角速度和不平衡功率；Mi为第i台发电机的转动惯量；ΔT为数据时间间隔，本文仿真中取为0.01s。

实时分群的基本过程主要分为下面2个步骤。

a.实测广域测量系统（WAMS）每一个新时刻t数据更新后，根据式（1）计算当前时刻各发电机的预测功角，并将其从大到小对发电机排序。

b.计算上面序列中相邻2台机组的预测功角之差，选出最大的功角间隙作为分割线，间隙上面的机群为超前机群S，间隙下面的机群为落后机群A。

对超前机群S和落后机群A分别进行等值，2个机群的等值参量为：

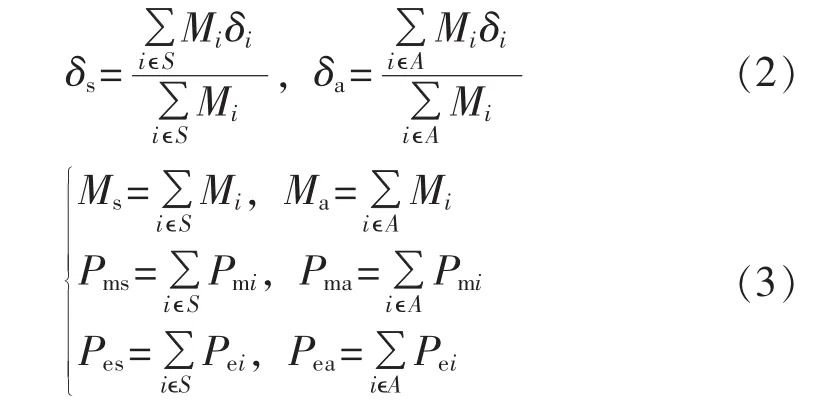
其中，δi、Mi、Pmi、Pei分别为第 i台发电机的功角、惯性中心、机械功率及电磁功率；Ms和Ma分别为S和A群等值惯量；Pms和Pma分别为S和A群等值机械输入功率；Pes和Pea分别为S和A群等值电气输出功率。

于是多机系统动态方程可简化为两机动态方程：

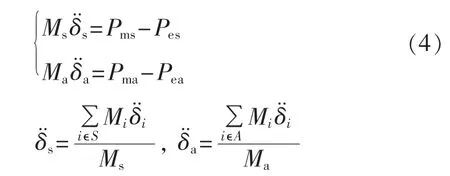
将两机系统进一步等值为单机无穷大系统：

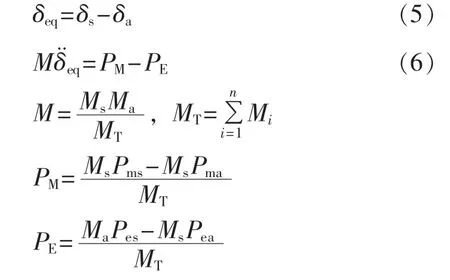
2 轨迹凹凸性判据在多机系统中的拓展

回顾本系列文章（一）[13]用相轨迹几何特征判别暂态不稳定的有关判据，相轨迹斜率为：

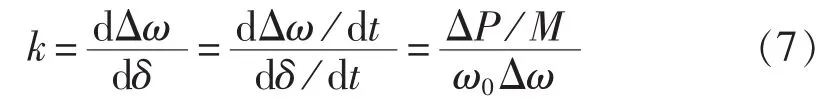
相轨迹拐点为：

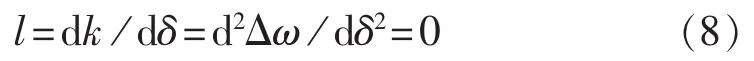
不稳定判据为：

拐点曲线附近相轨迹方向场为：

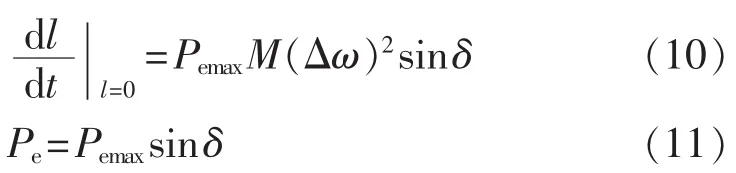
式（10）的推导过程中利用了式（11）简单电力系统中功率与功角的正弦关系[17]，从而获得功角在（0，π）范围内方向场的值总是正值唯一性，当满足条件lΔω＞0时，轨迹穿越拐点曲线由凹区域进入凸区域，系统失稳。

考虑到多机系统发电机励磁调节器、调频器等非自治因素的影响，等值系统的电磁曲线不再是理想情况下的正弦关系，相轨迹穿越拐点曲线后其方向场的方向不再唯一，等值相轨迹进入凸区域后，也有可能因为非自治因素的存在使其重新返回凹区域，因此，只采用本系列文章（一）[13]提出的不稳定指标τ对等值单机非自治系统进行稳定性判别时会出现误判情况。

定义一个表征拐点曲线附近轨迹方向场的辅助指标r，表示拐点曲线上功角与角加速度的二阶导数关系，其表达式如下：

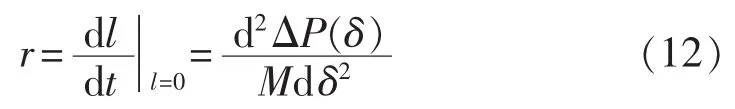
式（12）中变量均是可测量的物理量，因此指标r是可以通过WAMS的数据进行实时计算的。对式（12）进行数学变换：

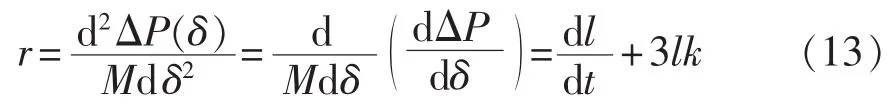
由式（13）可见，指标r在几何上反映轨迹凹凸性随时间的变化率。当轨迹位于上半平面内穿越拐点曲线进入凸区域（l＞0）且指标r＞0时，表示凹凸性对时间的变化率 dl/dt＞-3lkω0，由本系列文章（一）[13]知相轨迹在穿越拐点曲线时相轨迹斜率k为负值。r＞0表示轨迹以一定的速度穿越拐点，随时间增长向凸区域内持续发展而不会停留在拐点附近。

当相轨迹位于下半平面穿越拐点进入凸区域（l＜0），此时若辅助指标 r＜0，根据与上面相似的结论，可以得出轨迹穿越拐点进入凸区域后有一定的速度向凸区域持续发展，轨迹反向失稳。

综上2种情况，多机系统中不稳定判别的辅助指标可以记为μ=rΔω＞0，表示轨迹由凹区域以一定的速度穿越拐点进入凸区域，不会停留在拐点邻域内，从而导致系统失稳。辅助指标μ的离散形式：

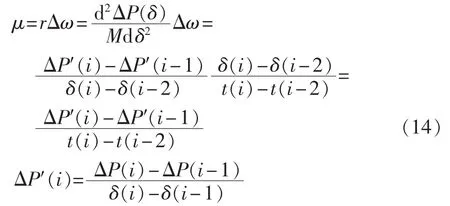
由于式（14）中分母总是大于零，因此辅助不稳定判据可以简化为：

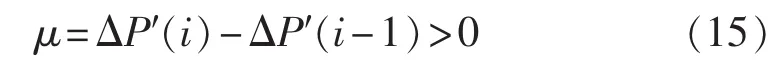
对于多机系统的不稳定综合判据为：

这样就考虑了时变性导致拐点曲线附近方向场变化使得轨迹返回的误判案例。仿真证明，加入辅助判据后，能够极大地减少对系统稳定情况下的误判，而对系统失稳情况下的检测速度几乎没有影响。

3 基于响应的多机系统不稳定性判别流程

根据不稳定指标τ和辅助不稳定指标μ，对多机非自治系统暂态不稳定性的实时判别流程如下。

a.检测到大扰动发生则启动以下流程。

b.读入当前时刻的实测数据，包括各发电机的功角、角速度和不平衡功率信息，并用式（1）进行各机组功角预测。

c.按照预测功角间间隔实时分为2群。

d.根据式（2）—（6）进行系统等值计算，将多机系统等值为一个单机非自治系统。

e.根据式（9）、（15）分别计算不稳定指标τ和 μ。

f.若满足式（16），判定系统将会失稳，输出判定结果，进入控制量计算及实施控制环节，完成后回到步骤b；否则，直接回到步骤b等待下一时刻数据读入。

4 算例仿真

为了验证上面提出的基于响应的多机电力系统暂态不稳定性实时判别方案，用仿真软件PSASP对IEEE标准10机39节点系统和三华实际大电网做了大量的仿真，用仿真输出的故障切除后一段数据作为WAMS的实测数据，并将仿真所得稳定结论（需要仿真几秒钟暂态的过程）与本方法的判别结果（仅需要更短时间采样的过程）比较，验证了该方案的可行性。

4.1 IEEE 39节点系统

IEEE 39节点系统接线如图1所示。该系统有10台发电机组，采用E′q恒定模型，带调压器、调速器和PSS，负荷用综合负荷模型，是一个多机的非自治电力系统。

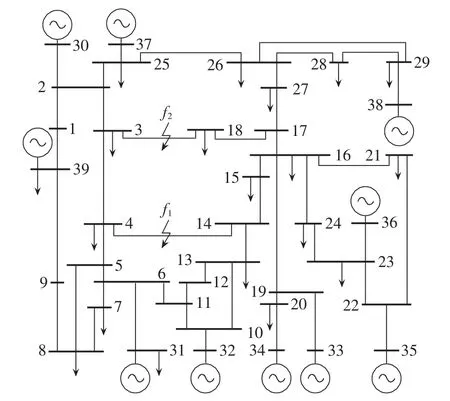
图1 IEEE 39节点系统接线图Fig.1 Connection diagram of IEEE 39-bus system

4.1.1 不稳定判据准确性和快速性的考察

故障1为设置在母线4、14之间线路的三相接地短路，不同的切除时间tc切除该线路。故障2为设置在母线3、18之间线路的三相接地短路故障，不同的切除时间tc切除该线路。通过反复仿真可以获得故障1的临界切除时间tc1，1为0.19s，故障2的临界切除时间tc1，2为0.29 s。表1为对不同故障切除时间下系统稳定性的判定结果与实际系统稳定性的对比。

表1 暂态稳定性识别方案在IEEE 39节点系统中的仿真结果Tab.1 Simulative results of transient stabilitydetection scheme for IEEE 39-bus system

对表1故障的切除时间相差10 ms、仿真结果分别为稳定和不稳定的临界情况，本文的判据能够给出准确的判定结果。不稳定越严重（故障持续时间越长），不稳定的判别越快，功角摆开越小，对后续紧急控制措施投入越快，对系统重新恢复平衡越有利。

4.1.2 附加判据有效性的考察

在故障2发生后0.29 s切除时，图2给出在2 s时系统功角曲线及分群情况，可见首摆临界稳定。

对应的相平面等值轨迹见图3（图中角速度为标幺值，后同）。电网非自治因素的存在，使得轨迹在1.4～1.6 s期间由凹区域进入凸区域，在1.6 s后仍能够重新返回凹区域，最终系统稳定下来。

图2 系统轨迹曲线及分群结果Fig.2 System trajectory curves and results of group division

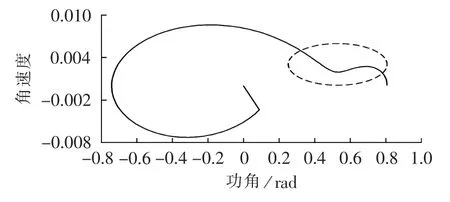
图3 临界稳定等值相轨迹曲线Fig.3 Equivalent phase trajectory curve of system with critical stability

其等值的功率－功角曲线见图4，图中等值功率为标幺值。从图4中可以看出，电磁功率和功角不再是严格的正弦关系，从而轨迹经过拐点曲线时的方向场是不确定的，这也导致单纯使用本系列文章（一）[13]中的不稳定指标τ会发生误判，见图5。这种临界稳定情况在辅助指标μ的作用下才能获得正确的判定结果。

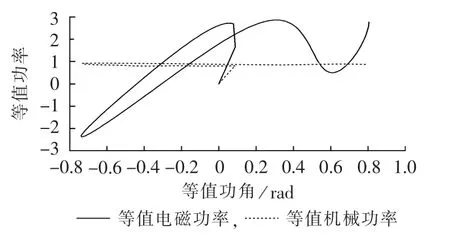
图4 临界稳定等值功率－功角曲线Fig.4 Equivalent power-power angle curves of system with critical stability

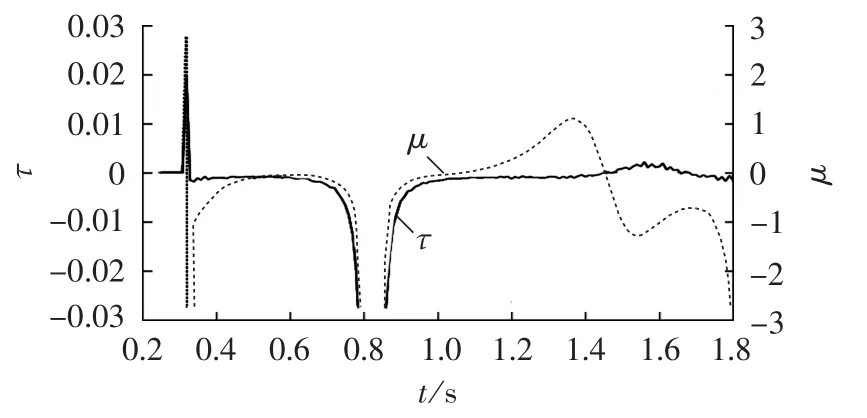
图5 临界情况下不稳定指标τ和μ的变化曲线Fig.5 Variation curve of instability index τ and μ in critical stability

考察本文提出的辅助指标μ在1.4～1.6 s时段为负，表明系统的非自治因素的阻碍不一定会导致系统不稳定。联合使用不稳定指标τ和μ的性质，在1.4～1.6 s避免了误判。

在故障2发生后0.30 s将其切除，系统暂态临界不稳定。在1.07 s时正确识别出系统失稳，此时系统的等值功角为166.3°，此时系统功角曲线及实时分群情况如图6所示。

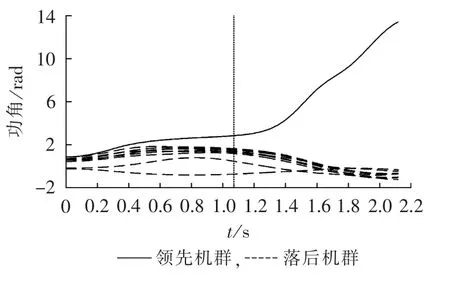
图6 系统功角曲线及分群结果Fig.6 System power angle curves and results of group division

图7为实时分群等值计算的不稳定指标随时间变化的曲线，到1.07 s时不稳定指标τ和μ同时满足式（16），判别出系统暂态不稳定，系统的等值功角为2.9 rad（约为166.3°），如图7中竖线所示。图中不稳定指标的突变是由分群模式发生变化产生不同的等值系统导致的。

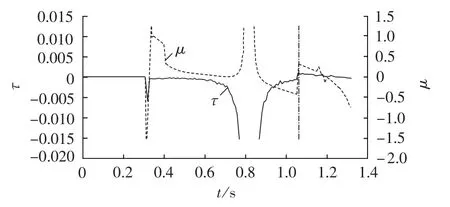
图7 实时分群的不稳定指标τ和μ的变化曲线Fig.7 Variation curve of instability indexτ and μ in real-time group division mode

如果按照此时分群模式进行等值分群，追寻其等值轨迹的不稳定指标曲线如图8所示。

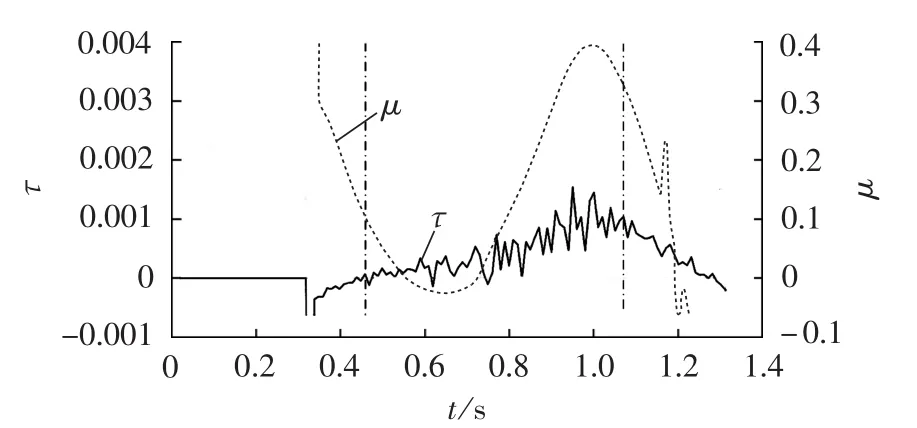
图8 固定分群方式下指标τ和μ的变化曲线Fig.8 Variation curve of indexτ and μ in fixed group division mode

由图8可以看出，早在0.46 s时不稳定指标τ和μ同时满足式（16），对比图6的功角曲线，显然当时的具有失稳趋势群与最终失稳群不同，会导致控制措施不当。其他的算例表明，如果不实时分群，会发生稳定与不稳定的误判。实时分群尽管有时会导致判稳时间推迟，但是保证了判别的准确性。

4.2 三华联网大系统

中国电科院对我国三华联网后（1614台发电机）的实际系统进行了典型故障下大量的暂态稳定及其控制计算，获得了多组仿真计算数据，以该计算数据代替WAMS的实测数据，验证本文方法在大型系统区域间不稳定及控制后稳定性判别的有效性。故障分别为主保护切除短路线路、主保护拒动后备保护切除短路线路、直流双极闭锁后联切发电机等多种事件。本方案的判别结果与判定时间如表2所示。

以复奉直流双极闭锁故障为例，系统在0 s双极闭锁，在0.1 s切除发电机，切除5台机时三华系统分为两群失稳，功角曲线及此刻的分群方式见图9。

观察图9可知，不同时刻各发电机功角间隔是变化的，其分群的结果不同，等值的轨迹不同，在2.61 s时判出系统不稳定，其机群分组如图9中虚线所划。按照2.61 s时的分群结果，追寻从故障开始后按该固定群等值后不稳定指标的变化曲线如图10所示。在1.4～2 s时段中，不稳定指标多次满足，将会出现失稳机群的误判。而按照实时分群的等值系统计算，不稳定指标并不满足，只有实时正确分群才能获得正确的判别结果。

表2 暂态不稳定性判据在三华系统中的验证Tab.2 Verification of transient instability criterion by Sanhua system

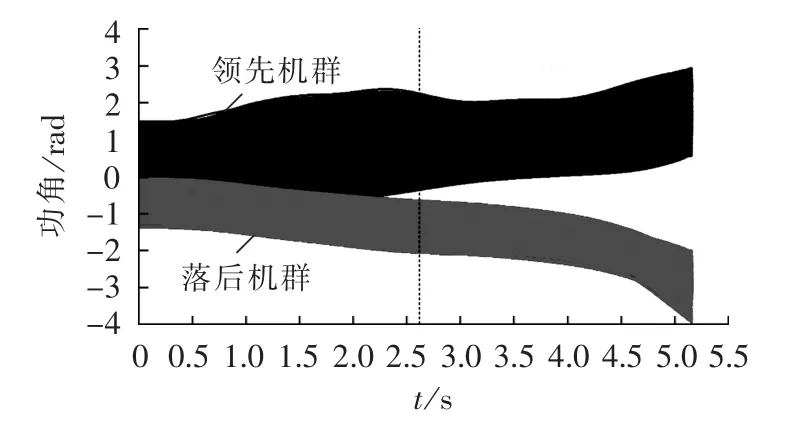
图9 切5台机后系统功角曲线及分群结果Fig.9 System power angle curves and group divisionresults after cutting off five generators

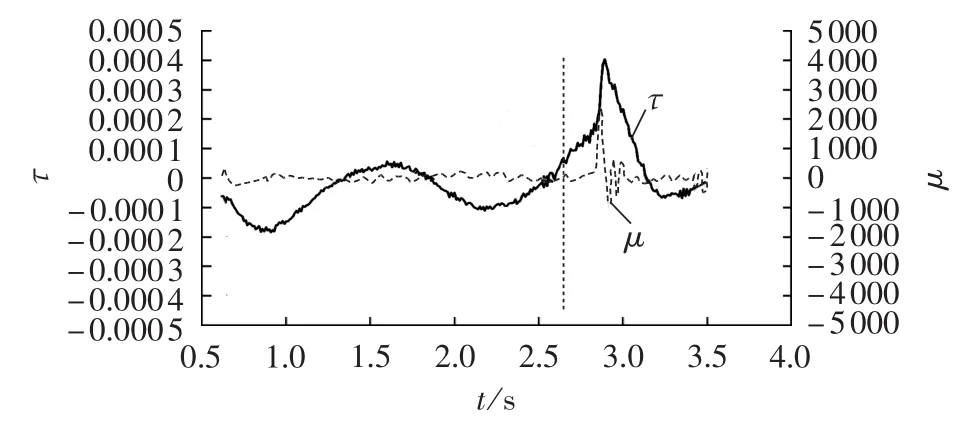
图10 切5台机后不稳定指标τ和μ的变化曲线Fig.10 Variation curve of instability indexτ andμ after cutting off five generators

对应此时分群结果，系统等值相轨迹曲线如图11所示，虚线表示检测出系统暂态不稳定性的时刻。判定出不稳定时系统的等值功角仅为2.407 rad（约为 138°）。

如果系统在奉贤直流闭锁0.1 s后切除6台发电机，则系统是稳定的，功角曲线如图12所示。

按照实时分群等值后不稳定判别指标τ和μ变化曲线如图13所示，始终不同时满足失稳判据式（16），判别方案正确有效。

图11 切5台机后等值系统不稳定相轨迹曲线Fig.11 Equivalent phase trajectory curve of instable system after cutting off five generators

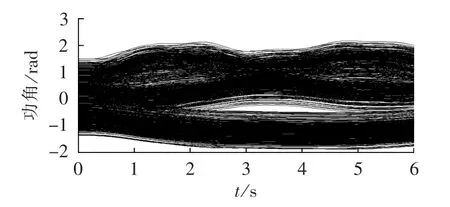
图12 切6台机后系统稳定功角曲线Fig.12 Power angle curves of stable system after cutting off six generators

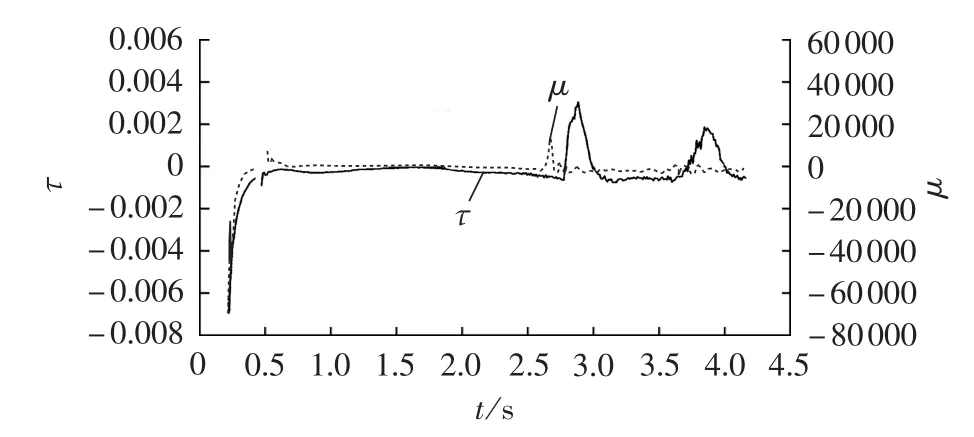
图13 切6台机后不稳定指标τ 和μ的变化曲线Fig.13 Variation curve of instability indexτ and μ after cutting off six generators

5 结论

多机系统的暂态不稳定识别可以通过实时识别同调机群的方法将其等值为一个单机非自治系统的稳定性识别问题，本文提出的功率－功角平面的特征识别对于适应实际系统中非自治因素对不稳定的影响是有效的，组合本系列文章（一）[13]的不稳定判据，在实际的多区域互联大电网中基于响应的暂态不稳定快速判别是准确、快速的。系列扰动后的仿真结果表明，本文的不稳定判别方法适应多次控制后的响应，为启动闭环控制奠定了必要性基础。