非线性电力系统模型经验Gramian平衡降阶

赵洪山，薛 宁，时 宁

（华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003）

0 引言

目前，在电力系统计算、仿真、分析与控制过程中，经常采用非线性高阶动态模型来提高描述系统动态行为的能力，但同时带来了系统模型动态方程维数高、模型计算的复杂度（包括计算时间、速度以及存储空间等）增加等问题，给工程研究人员带来了巨大的挑战。尤其对于多机电力系统，随着系统规模不断增大，其动态模型的阶数也随之增加，这使得通过计算系统模型来快速完成各种功能变得非常困难[1-3]。

模型降阶是解决上述非线性电力系统模型高维动态行为计算复杂、难以分析等问题的有效方法之一。学者们也已进行了大量研究，如奇异值摄动法[4-7]、解耦算法[8-10]、同调等值理论[11-14]、模态分析方法[15-16]、基于相关性的模型降阶方法[17]以及基于Krylov子空间的模型降阶方法[18]。但上述系统模型降阶多用于分析研究，较少关注系统的输入控制，或将输入控制作恒定处理；而应用于控制设计的系统模型降阶，则需要考虑降阶模型是否能够保持原系统的动态行为和输入/输出特性的问题。

在众多模型降阶方法中，Gramian方法已在线性电力系统广泛应用。文献[19]为了简化区域电网振荡阻尼控制器的设计，利用Gramian方法研究了电力系统模型降阶，并验证基于降阶系统设计的控制器没有降低原系统闭环特性的结论；文献[20]也在抑制低频振荡问题上利用Gramian降阶方法研究了更大规模电力系统的模型降阶问题。但对于一般非线性动态电力系统模型降阶，由于缺少有效的理论方法，其模型降阶仍是研究的难点。本文利用经验Gramian方法和平衡实现理论，探讨非线性电力系统动态模型的降阶过程，并以某实际多机非线性电力系统为例，验证经验Gramian降阶方法对非线性电力系统模型降阶的有效性。

1 非线性系统模型平衡降阶基本原理

1.1 模型降阶基本思想

具有输入和输出的非线性系统模型一般可以表示为：

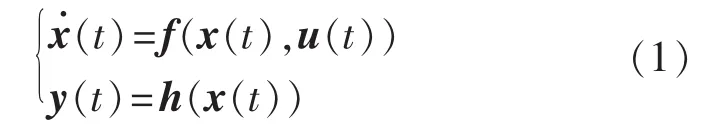
其中，f（x，u）描述非线性系统的动态行为；x（t）єRn为非线性系统的状态变量；u（t）єRp为非线性系统的控制输入；y（t）єRq为非线性系统的输出。

模型降阶的基本思想就是对形如式（1）的非线性动态系统，通过已知标准列正交转换矩阵，将原系统变换到一个低维空间Rk（k≤n）上，并可用低维空间中的降阶系统来表示原系统，从而降低了原系统理论分析难度和数据运算量。假设已知转换矩阵P，由原始非线性系统（1）可以得到降阶系统：

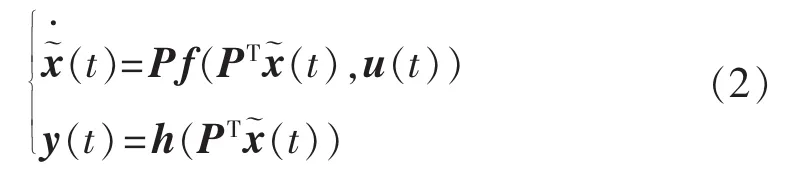
1.2 Galerkin投影

目前，模型降阶中最重要和最基本的方法就是Krylov子空间类方法，经验Gramian方法也基于Krylov子空间原理，即通过构建转换矩阵P来进行模型降阶。其中，矩阵P是由Galerkin投影获得的。

Galerkin投影：一旦得到子空间的特征函数，就可以利用Galerkin投影将系统（1）投影到该子空间。Galerkin投影矩阵P通常可表示为：

其中，Ik×k为 k×k 阶的正交矩阵；0k×（n-k）为 k×（n-k）阶的全零矩阵。 因此，非线性降阶系统（2）中，有 class="picture_character" src="images/2bdd96436f03e63f1ee327b703d8a6f2.png" />（t）=Px（t）。

1.3 经验Gramian矩阵

对于一般非线性系统（1），其输入与输出特性通常由系统的可控Gramian矩阵Wc和可观Gramian矩阵Wo来描述，可控Gramian矩阵描述控制输入变化对系统状态的影响，而可观Gramian矩阵描述输出对系统状态变化的反应。

对于线性系统，其模型降阶可通过求解Lyapunov方程获得可控Gramian矩阵和可观Gramian矩阵，然后通过分析Gramian矩阵的特征值，来确定线性系统模型的降阶阶数[21]。而对于非线性系统，由于无法获得Lyapunov方程，目前仍没有直接计算可控Gramian矩阵和可观Gramian矩阵的解析方法。Sirovich在文献[22]中提出：通过仿真或实验获得系统状态变量和输出变量样本，再根据采样的经验数据样本，计算得到非线性系统模型的经验可控Gramian矩阵和经验可观Gramian矩阵。

经验Gramian方法得到的系统数据样本应满足在其稳定域内这一条件，并且要尽可能反映各种可能的扰动行为。为此，定义如下集合：

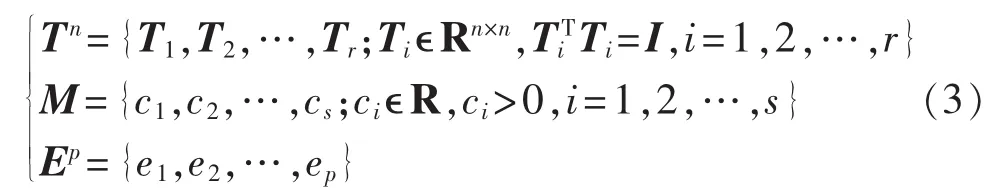
其中，Tn为一组r个正交的n×n阶矩阵，r为激励或者扰动方向的矩阵数量；M为一组s个正常数，s为在每个方向不同扰动大小的数量；Ep为Rp中标准单位矢量。

定义1设Tn、Ep和M为以上所给定集合，对于非线性系统（1），经验可控Gramian矩阵Wc定义如下：

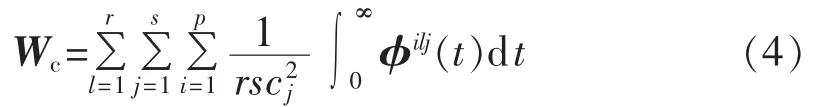
对于具有输入和输出的可控非线性系统，只研究输入与状态的行为是不全面的，同时也应考虑输出反映系统状态的行为。下面定义给出了经验可观Gramian矩阵的构建方式。

定义2设Tn、Ep和M为以上所给定集合，对于非线性系统（1），经验可观Gramian矩阵Wo定义如下：

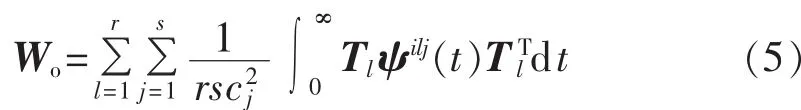
对经验可控和可观Gramian矩阵分别进行奇异值分解，其非零特征值所对应的特征向量就可生成一个新子空间，然后可以将系统（1）投影到该子空间，得到降阶系统（2）。由此，实现了反映系统可观性与可控性非线性系统的模型降阶。

1.4 基于经验Gramian平衡降阶

由上文可知，一旦得到非线性系统（1）的可控与可观Gramian矩阵，便可对其进行奇异值分解，并利用可控或可观Gramian矩阵的奇异值大小来确定Galerkin投影矩阵P，进而得到降阶模型的阶数。但对于一般非线性系统，直接得到的可控或可观Gramian矩阵往往是不相同的，如果以可控Gramian矩阵的奇异值进行降阶，降阶系统的可控性获得较好的性能，但系统的可观性稍差；反之，以可观Gramian矩阵的奇异值进行降阶，降阶系统可得到较好的可观性，可控性能稍差。

为了使降阶系统的可控性和可观性都能获得较好的性能，利用平衡实现理论对非线性系统（1）进行处理，将经验可控与可观Gramian矩阵变换成平衡的可控和可观Gramian矩阵，即将系统（1）变换成平衡系统。所谓平衡系统，是指系统的可控Gramian矩阵与可观Gramian矩阵是相等的，并且是对角的。下面给出了利用经验可控Gramian矩阵Wc和可观Gramian矩阵Wo计算系统（1）的平衡系统的步骤。

a.对经验Wc和Wo，进行Cholesky因式分解，得到矩阵X和Y。

b.构建积矩阵YTX，并对积矩阵进行奇异值分解，得到对角矩阵∑、正交矩阵U和V。

其中，∑ єRn×n为 Hankel奇异值矩阵。

c.根据式（8）可获得平衡转换矩阵T。

至此，利用该平衡变换矩阵T就可获得系统（1）的平衡系统：

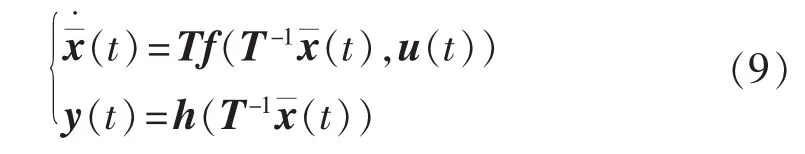
平衡系统与其原系统的动态行为是完全相同的，只是平衡系统的状态变量变为一组新的状态变量。从线性系统理论而言，平衡系统任一状态都是原系统所有状态的线性组合，即。 因此，对非线性系统（1）进行模型降阶，若可控和可观Gramian矩阵不等，就可先把系统转换成平衡系统，再对平衡系统进行模型降阶，该过程称为平衡实现。

针对非线性系统对应的平衡系统，计算其经验Gramian矩阵，并对经验 Gramian矩阵和进行奇异值分解。根据Hankel矩阵∑奇异值σ的大小，当满足σk≫σk+1或者当前k个奇异值能量所占所有奇异值能量绝大部分时，就认为k后面的奇异值所对应的状态变量对系统的输入影响和输出影响较小，将其略去以实现模型降阶的目的。因此，可以将分为主要和非主要两部分，如下：

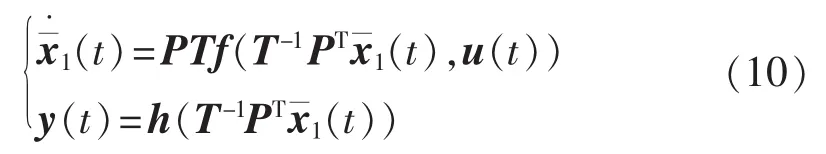
2 非线性电力系统经验Gramian模型降阶

2.1 非线性电力系统模型

假设多机电力系统有Z台发电机，同步发电机采用计及转子超瞬变过程且转子q轴要考虑阻尼绕组的6阶动态模型。第i台发电机模型描述如下：

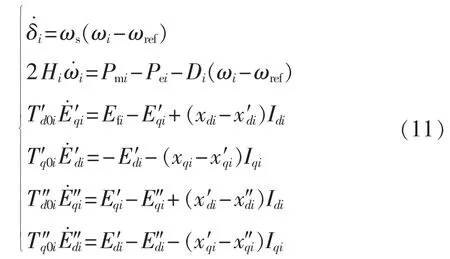
其中，i=1，2，…，Z；δi为第 i台发电机转子角；ωi为第i台发电机角频率；E′di、E′qi、E″di、E″qi分别为第i台发电机d轴和q轴暂态电势和次暂态电势；ωs为发电机额定角频率；ωref为发电机参考角频率；Pmi为第i台发电机的原动机输出机械功率；Pei为第i台发电机的电磁功率；Hi为第i台发电机机组惯性时间常数；T′d0i、T′q0i、T″d0i、T″q0i分别为第i台发电机d轴和q轴开路暂态、次暂态时间常数；Efi为第i台发电机机组的励磁电压；Di为第i台发电机定常阻尼系数；rai、xdi、xqi、x′di、x′qi、x″di、x″qi分别为第i台发电机定子电阻和d 轴和 q 轴暂同步、瞬变、超瞬变电抗；Idi、Iqi、Udi、Uqi分别为第i台发电机d轴和q轴暂态电流和机端电压，其关系为Udi=E″di-raiIdi-x″qiIqi，Uqi=E″qi+x″diIdi-raiIqi。

发电机与网络的接口方程为：

其中，Ixy=CSIdq；Uxy=CUdq；C 为 dq－xy坐标系的变化矩阵；S为网络容量和发电机容量之间的变化矩阵；Ys为电力系统节点导纳矩阵。

将xy坐标下的Ixy和Uxy转换到dq坐标系下，代入式（12），消去Idi和Iqi，得到如下形式的具有输入和输出多机非线性电力系统模型：

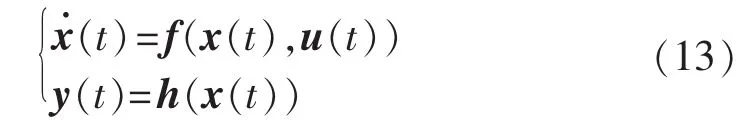
其中，u（t）=[Pm1… PmZEf1… EfZ]TєRp；x（t）=[δ1…δZω1…ωZE′q1…E′qZE′d1…E′dZE″q1…E″qZE″d1…E″dZ]TєRn；f（x，u）描述电力系统动态行为；y（x）为系统的输出函数，由关于状态x（t）的非线性函数来表示。

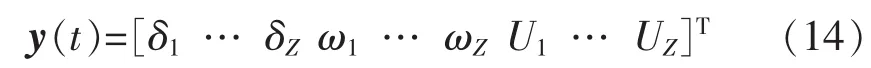
其中，Ui为第 i台发电机机端电压；y（t）єRq。

2.2 非线性电力系统经验Gramian矩阵

对于非线性电力系统（13），其经验可控Gramian矩阵和可观Gramian矩阵的计算，由于涉及积分计算，计算量非常庞大。假设系统的样本是在离散时间t1、…、tm得到的，那么状态或输出的相关矩阵可以写成如下离散形式：

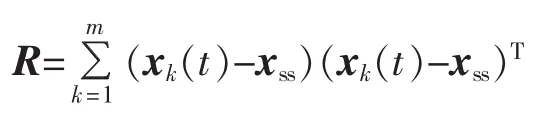
其中，xk（t）为系统的样本值；xss为系统状态的稳态值。

下面分别给出了经验可控和可观Gramian矩阵的离散定义。

设Tn、Ep和M为前文所给定的集合，p为系统的控制输入个数，则系统经验可控Gramian矩阵Wc定义为：

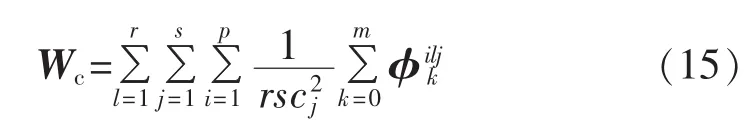
设Tn、Ep和M为前文所给定的集合，则系统经验可观Gramian矩阵Wo定义为：

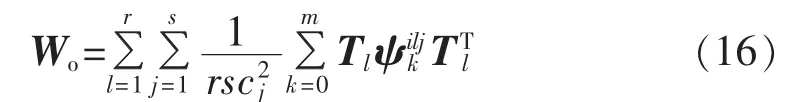
利用经验样本数据，通过式（15）和（16）便可计算出非线性电力系统（13）的经验可控Gramian矩阵Wc和经验可观Gramian矩阵Wo，其计算精度取决于样本个数，样本数量越大，精度越高；此外，还受外加激励大小的选择cj、外加激励方向的选择Tlei以及外加激励的个数p等因素的影响。

2.3 基于经验Gramian的非线性电力系统平衡降阶步骤

对于非线性电力系统动态模型（13），利用经验Gramian进行平衡降阶方法的步骤如下。

a.根据定义（15）和（16），计算非线性多机电力系统（13）的经验可控Gramian矩阵Wc和经验可观Gramian 矩阵 Wo。

b.利用式（6）—（8）计算平衡变换矩阵 T，得到非线性多机电力系统（13）的平衡系统模型。

c.利用平衡变换矩阵T，计算平衡系统的经验可控Gramian矩阵和经验可观Gramian矩阵：

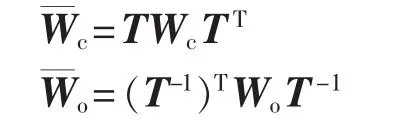
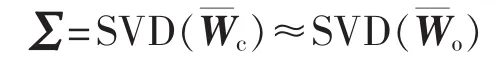
e.确定非线性多机电力系统降阶模型的阶数。如果满足

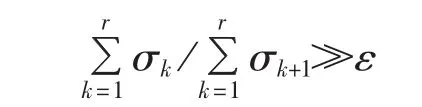
则平衡系统的降阶模型的阶数为r。其中，ε为接近于1的值。利用阶数r构造Galerkin投影矩阵P。

f.利用平衡变换矩阵T和Galerkin投影矩阵P，计算得到形如式（10）的电力系统平衡降阶模型。

3 算例分析

对某实际20机电力系统模型进行降阶仿真分析，系统接线图见图1。

首先，形成多机电力系统分析模型，每台同步发电机采用6阶动态模型，负荷为恒阻抗模型。由于发电机模型采用dq坐标，网络模型采用xy坐标，因此，需要xy-dq坐标变换实现发电机与网络的互联，其过程见式（11）—（13），最后形成一个 120阶的形如式（13）的非线性电力系统动态模型。

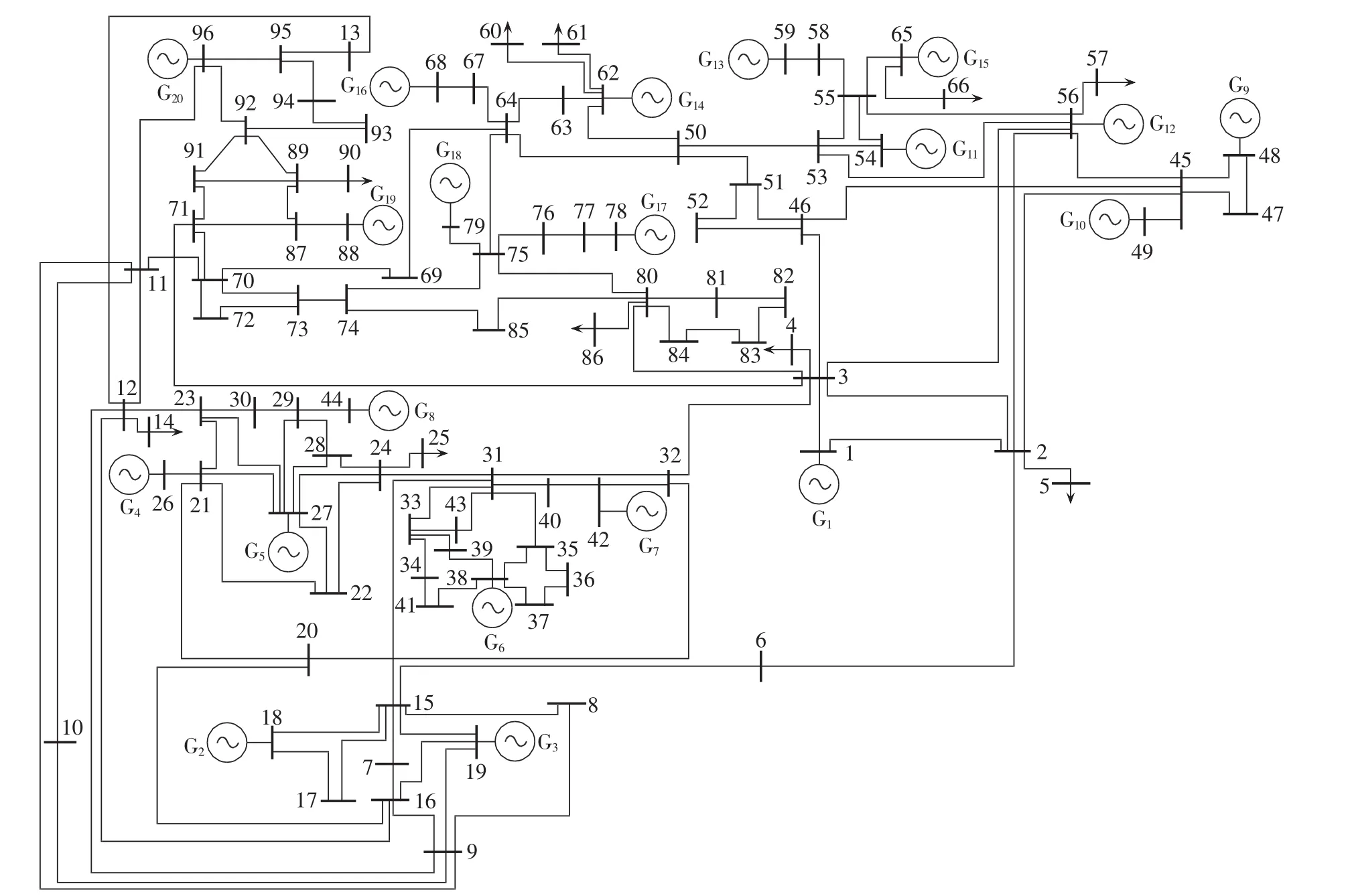
图1 某实际20机系统接线图Fig.1 Connection diagram of an 20-generator power system

图1 某实际20机系统接线图Fig.1 Connection diagram of an 20-generator power system

其次，利用经验Gramian平衡降阶算法，计算上述非线性电力系统的平衡变换矩阵T，得到该系统的平衡系统。对平衡系统的经验Gramian矩阵进行奇异值分解，利用奇异值分解得到Hankel奇异值矩阵∑，奇异值大小分布如图2所示。

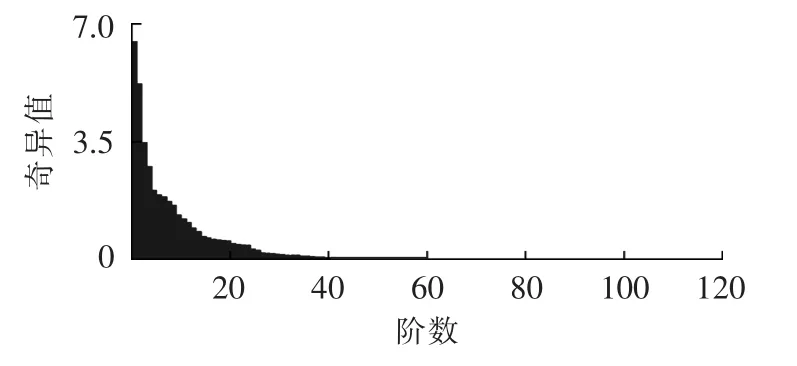
图2 Hankel奇异值的分布图Fig.2 Distribution of Hankel singular values

最后，利用Hankel奇异值大小，根据模型降阶阶数判定条件确定降阶系统的维数，得到Galerkin投影矩阵P。由此，利用平衡变换矩阵T和投影矩阵P，得到20机非线性电力系统的降阶模型。

从Hankel奇异值角度分析，当ε取0.99，可以将原120阶非线性电力系统投影到50维的子空间中；当ε取0.95，可将原系统降为32阶的非线性动态系统。理论上，ε取值越小，降阶系统的阶数就越小，但投影到子空间后的动态行为失真就越大。因此，需要合理选择降阶模型的阶数。

对于该20机实际电力系统，每台发电机均考虑调速控制和励磁控制功能，这些控制器的参数在各降阶系统中都保持不变。在考虑三相短路故障（故障点在线路33－34之间50%处）情况下，对各降阶模型的暂态动态变化过程进行仿真分析。为了节省篇幅，以发电机7为例，给出了其相应的仿真曲线如图3—5所示。图中，功角δ、角速度ω、输出电压Ut均为标幺值。

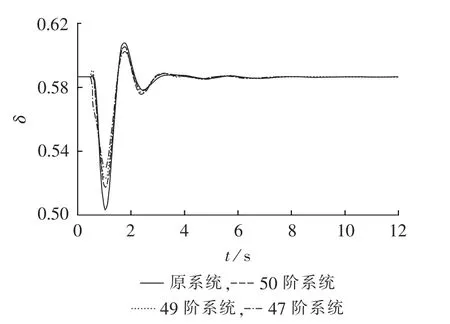
图3 降阶系统与原系统功角仿真曲线Fig.3 Simulative angle curves of reduced system and original system

图4 降阶系统与原系统角速度仿真曲线Fig.4 Simulative angular speed curves of reduced system and original system

图5 降阶系统与原系统输出电压仿真曲线Fig.5 Simulative output voltage curves of reduced system and original system

从仿真曲线图3—5中可以看出：对于50阶的降阶系统，除功角幅值误差稍大些外，角速率和电压幅值与原系统输出相比误差都很小，而且3个输出响应的频率特性（即暂态过程）与原系统的几乎相同；当系统降到49阶时，功角、角速度和电压幅值3个输出响应的幅值变化不大，但较50阶的降阶系统，其与原系统的误差要比50阶系统大，并有逐步增大的趋势。尤其，当系统降到47阶或低于47阶时，降阶系统输出响应的幅值误差增大，观察功角和角速度曲线出现频率偏移，即产生了频率失真。从Hankel奇异值角度分析，投影到50维子空间的能量约为原系统能量的99.45%，其能保留原系统的大部分能量，即保留了原系统的各种特性和动态行为。

通过对所有节点仿真曲线进行统计分析可知：当ε选择大于0.99时，降阶模型的误差都比较小，能够将原系统的输入和输出动态行为保留下来。为了使降阶系统得到较为精确的幅频特性，通常选择ε为0.99。本例中，降阶系统模型的阶数可降到50阶，其所有节点状态和输出与原系统相比，误差都非常小。

4 结论

本文提出了一种针对多机非线性电力系统模型的经验Gramian平衡降阶方法，并通过某实际20机非线性多机电力系统模型进行仿真验证。仿真结果表明：降阶系统能够很好地保留原非线性电力系统输入和输出的动态行为以及原非线性电力系统的稳态值。对于该20机非线性电力系统，可以将120阶非线性动态模型降到50阶，仿真结果证实了所提方法在非线性电力系统模型降阶中的有效性。