空间粒子群优化算法及其在电力系统环保经济负荷分配中的应用

周任军，李绍金，李红英，康信文，刘乐平，周胜瑜

（长沙理工大学 智能电网运行与控制湖南省重点实验室，湖南 长沙 410114）

0 引言

经济负荷分配ELD（Economic Load Dispatch）是在满足系统负荷和运行约束条件的前提下，电力系统或电厂内合理分配各机组负荷，使发电成本最小化的电力系统典型优化问题。由于环保问题受到重视，其优化目标中不仅考虑发电燃料成本或市场经济，并且考虑 CO2、NOx和 SO2等排放最小[1]。

在经济调度优化问题的计算方法中，智能算法由于对变量和函数不要求连续可微，在解决非线性、非凸性、不连续优化问题中得到了广泛的应用和认可[2]。但其计算结果随机性较大，算法全局收敛性较差。因此，在基本智能算法的基础上，形成了结合遗传算法全局搜索能力强和禁忌搜索爬山能力强的优势的混合算法[3]；但是这类混合算法计算量大、时间较长，并且随机性问题难以得到改善，使得其难以胜任实时在线调度优化问题。粒子群优化PSO（Particle Swarm Optimization）算法由于其快速、简便而被逐渐应用和改进。引入随机变异算子[4]、融入禁忌搜索思想[5]、采用自适应变异算子的自调节[6]、随机黑洞处理与聚类[7]等方法引入了全局搜索信息，增加了解的多样性；而改进的混沌粒子群优化算法则通过修正粒子群迭代的行动策略，并引入混沌映射，加强了适应度值较优的粒子的全局搜索能力[8]。这些文献主要是改进了解的搜索方式或者融合了其他算法的优势，在一定程度改善了过早收敛的缺陷，但效果不太令人满意，并且计算结果的随机性问题仍很突出。

这些粒子群优化算法及其改进均是通过速度和位置2类参数对多维的控制变量进行寻优和修正，其寻优过程有如在绵延山群中，站在每个山腰均容易得到所在山头的制高点，即局部最优点；但是若要寻求整个山脉的最高处，则需要空中俯视，改变寻优视角。因此，可通过增加一类参数，即高度参数，将高度与速度、位置共同组成一个寻优空间，探索一种新型的空间粒子群优化SPSO（Space Particle Swarm Optimization）算法。

空间粒子群中高度参数的引入，使所有粒子移动的方向和距离都是由其速度和高度共同决定，构成位置、速度、高度3类参数空间；此时群体中的所有粒子对应的每一维变量均跟随最优粒子对应变量在一个全新的空间解域内搜寻，可有效解决算法易陷入局部最优、收敛过早的缺陷，同时粒子群在高度参数的作用下，易于跳出早熟区间，并且降低寻优随机性。

1 环保经济负荷分配数学模型

1.1 发电燃料成本

发电燃料成本是指发电机组在发电过程中燃料消耗花费，单台发电机一般可用二次函数近似表示为：

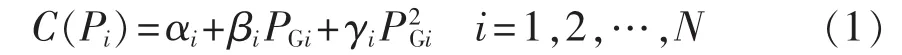
其中，C（Pi）为第 i台发电机燃料消耗费用（$/h）；Pi为第i台发电机的有功功率；N为系统发电机总数；αi、βi、γi为第 i台发电机燃料消耗特性曲线参数（已经折算成钱），均为常数。由此系统总燃料花费f1（$/h）可表示：

1.2 环境成本

将污染气体综合排放量与对应气体单位排放价格之积作为环境成本，污染气体主要包括CO2、SO2、NOx等，通过排放量和折价标准折算出环境成本[9]。则在单位时间内所产生的各类污染气体排放量（t/h）分别为：

其中，eCi（Pi）、eSi（Pi）、eNi（Pi）分别为第 i台发电机单位时间内 CO2、SO2、NOx的排放量；aCi、bCi、cCi、εCi和 λCi为第 i台发电机 CO2的排放参数（均为常数）；aSi、bSi、cSi、εSi和 λSi为第 i台发电机 SO2的排放参数（均为常数）；aNi、bNi、cNi、εNi和 λNi为第 i台发电机 NOx的排放参数（均为常数）。由此可得整个系统单位时间内污染气体总的排放罚款，即环境成本f2（元/h）可表示为：

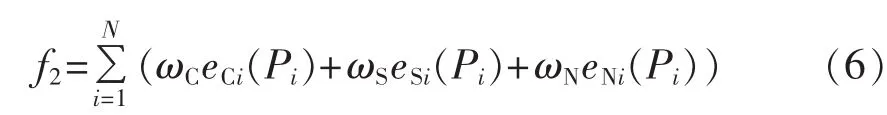
其中，ωC、ωS、ωN分别为 CO2、SO2、NOx对应的环境价值与由于排放所受到的罚款。

1.3 环保经济负荷分配优化模型

1.3.1 目标函数

环保经济负荷分配的目标是使系统发电燃料成本与环境成本之和达到最小值。因此，其优化目标函数可表示为：

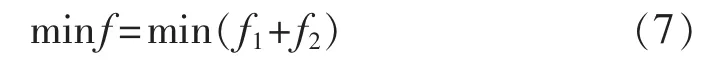
其中，f为系统总的发电综合成本（$/h）。

1.3.2 约束条件

a.发电机有功功率约束为：

其中，Pmaxi、Pmini分别为第i台发电机有功功率的上、下限值。

b.系统功率平衡约束为：

其中，Ploss、PD分别为系统的总网损和总负荷。另外，在处理等式约束（功率平衡约束）时，采用待定消元法将等式约束转换为不等式约束。任选一个发电机组，以第1台为例，可将式（9）变形为如下形式：

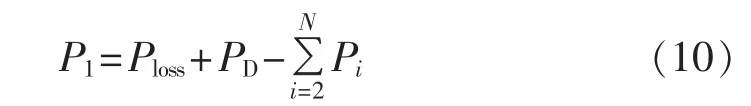
将式（10）分别代入到目标函数和不等式约束中，就可以消除等式约束，得到新的目标函数和不等式约束，这样不仅可以精确地处理等式约束，而且还减少了优化处理时变量的维数。

c.机组旋转备用容量约束为：

其中，SD为系统总的备用容量。

2 空间粒子群优化算法

2.1 经典粒子群优化算法及其改进

粒子群优化算法是人们受到社会体系中个体行为的启示而提出的一种优化算法，它通过群体的信息共享与个体自身经验的总结来修正个体行动策略，最终求取优化问题的解[10-12]。

在粒子群优化算法中，每个优化问题的未知解都可以作为搜寻范围内的一个点，即粒子。每个粒子都对应一个取决于待优化函数的适应度值，所有粒子移动的方向和距离都是由其速度决定的，并且群体中的所有粒子均跟随最优粒子在一个平面解域内搜寻。每次速度和位置的更新原则如下[13-15]：

其中，i=1，2，…，m（m 为种群规模）；j=1，2，…，D（D为未知量的个数）；c1和c2为学习因子；vkij、vkij+1分别为粒子i对应第j个变量在第k次、第k+1次修正时对应的速度；xikj、xkij+1分别为粒子i对应第j个变量在第k次、第k+1次修正时对应的位置；pikj为粒子i对应第j个变量在第k次修正时个体最优位置；pkgj为整个群体对应第j个变量在第k次修正时全局最优位置；r1、r2为介于0～1之间均匀分布的随机数。经典粒子群优化算法中惯性权重采用线性递减修正方式来更新权重值，具体修正模式如下[16]：

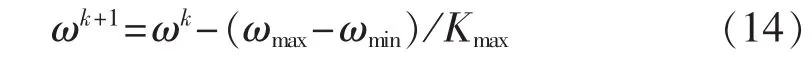
其中，ωk与ωk+1分别为粒子在第k次和第k+1次寻优所对应的惯性权重值；ωmax为最大惯性权重，通常经验取值为0.9；ωmin为最小惯性权重，通常经验取值为0.4；Kmax为预先设定的最大迭代次数。

经典粒子群优化算法虽然依赖经验参数少、操作原理简单、收敛速度快，但有易陷入局部最优、收敛精度不高、优化结果随机性大等缺陷。对此，相关研究主要从改进粒子自身速度修正方式或引入变异、扰动等改善全局搜索能力、增加粒子多样性；同时也与遗传算法、混沌优化等智能算法结合使用。

2.2 空间粒子群优化算法

与经典粒子群优化及其改进算法不同，所提出的空间粒子群优化算法不是在速度和位置等方面改进搜索，也不是重复经典粒子群优化算法的多维变量寻优空间；而是通过对每个粒子优化变量矩阵的每一分量附加一组高度参数，并与原来的位置和速度共同构成一个包含位置、速度和高度3类参数的参数空间；这样使得每个待优化变量由原来在以位置x和速度v所组成的平面域内寻优转变为在一个由位置x、速度v和高度h组成的全新空间域内寻优，即x－v－h 空间。 对于每一个粒子都对应一组（x，v，h），同时，位置x、速度v和高度h三者的更新策略也是相互影响的。此时，位置的修正方式发生了变化，按式（15）来更新。

其中，vk+1ij为粒子i对应第j个变量在第k+1次修正时对应的速度；hk+1ij为粒子i对应第j个变量在第k+1次修正时对应的高度。而速度的修正方式没有发生改变，同样根据式（12）来更新。

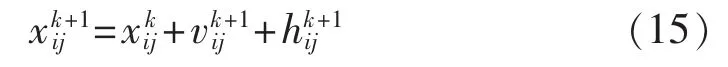
考虑到经典粒子群优化算法中粒子速度的更新已经融入随机优化理论，为了降低优化结果的随机性，高度参数h的更新不再引入随机理论，而是通过比较相邻2次优化结果对应的适应度值是否相等来选择高度修正方式。若当前粒子的适应度值与上一次寻优结果对应的适应度值相等，则根据当前适应度以及平均适应度来调整高度，具体更新方式如式（16）所示；否则维持高度不变。随着寻优过程的进行，当前后2次寻优结果相同时，对高度值进行调整，使其跳到另一个寻优区域，这样可以避免经典粒子群优化算法容易陷入局部最优解而不能跳出来的缺点；同时保证了搜索的全面性，增强了全局搜索能力；由于在高度修正策略中也综合考虑了整个群体的适应度值，这也保证了粒子的多样性。

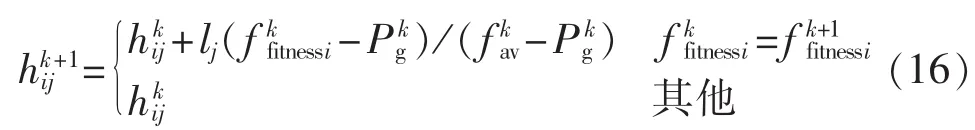
其中，fkfitnessi为粒子i在第k次修正时所对应的适应度值；fkav为所有粒子在第k次修正时所对应的平均适应度值；Pgk为所有粒子在第k次修正时所对应的最优适应度值；hikj、hkij+1分别为粒子i对应第j个待优化变量在第k次、第k+1次修正时对应的高度；lj为第j个变量对应的可行区间的长度。

综上所述，粒子i所对应的第j个待优化变量（xij，vij，hij），速度 vij侧重于调节粒子位置 xij的变化，仅决定着粒子位置xij的改变；若寻优前后2次结果所对应的适应度值不同，则hij保持不变，而此时位置xij将随着vij的变化而改变，即此时粒子等同于在一个纵向距离（高度）为hij、由x-v所组成的平面区域内寻优；否则，高度hij将按式（16）更新，此时原先由x-v所组成的平面区域的高度hij发生了改变。由此可以看出，高度hij不仅决定着粒子位置xij的变化，还控制着粒子速度vij和位置xij所构成寻优平面区域的纵向变化，可以使粒子跳出局部最优区域，进而到达一个新的寻优区域。

2.3 空间粒子群优化算法的基本步骤

运用空间粒子群优化算法解决实际问题的基本步骤如下所述。

a.参数的设定。最大迭代次数Kmax、粒子个数m、变量个数D、惯性权重ωmax和ωmin、学习因子c1和c2等参数设定。

b.初始化。每个粒子的位置、速度、高度、个体极值、全局极值初始化；对于适应度函数的确定，文中直接以目标函数作为适应度函数，则有：

c.数据更新。 根据式（12）、（15）、（16）分别更新每个粒子的速度 vij、位置 xij、高度 hij。

d.根据适应度评价函数更新数据。

e.判断是否满足终止条件。若不满足，返回步骤c；若满足，执行步骤 f。

f.计算结束，输出结果。

3 算例仿真结果分析

3.1 算例与参数处理

选取IEEE 30节点标准测试系统[17-18]为例，分别采用经典粒子群优化和空间粒子群优化算法进行环保经济调度的仿真计算。其中，系统的总负荷值PD=283.4 MW，系统的单线图见文献[19]，6个发电机组参数如表1所示。鉴于IEEE 30节点标准测试系统只给出了CO2的排放参数，因此文章计算环境成本时仅考虑了CO2的排放部分，其各机组CO2的排放参数如表2所示。取粒子种群规模m=40；学习因子c1、c2均取 1.5；惯性权重取 ωmax=0.9，ωmin=0.4；最大迭代次数为100次；旋转备用容量取符合需求的5%。并按电力行业排放标准设定各类污染气体单位排放量罚款，具体取值情况见文献[20]。

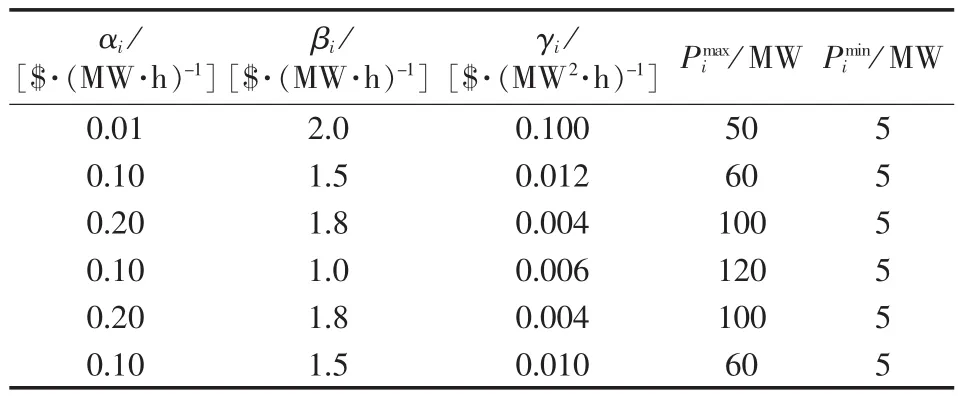
表1 发电机基本参数Tab.1 Basic parameters of generator

表2 机组的CO2排放参数Tab.2 CO2emission parameters of unit

3.2 仿真结果分析

针对上述案例分别采用经典粒子群优化算法、文献[4]中的改进粒子群优化（IPSO）算法和空间粒子群优化算法进行优化，在同等条件下，各自独立计算50次，其总成本的优化结果如图1所示。

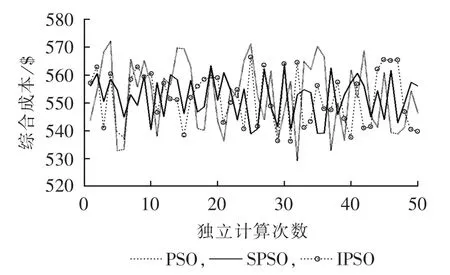
图1 综合成本优化结果分布Fig.1 Distribution of comprehensive cost optimization results

从仿真结果图1中可以看出，空间粒子群优化算法优化结果的随机性明显小于经典粒子群优化算法优化结果的随机性，同时也小于改进粒子群优化算法优化结果的随机性。分别对50次独立计算求得的总成本取平均值可求得：空间粒子群优化算法算得的综合成本为553.34$/h，粒子群优化算法算得的综合成本为572.46$/h，改进粒子群优化算法算得的综合成本为560.37$/h。可以发现空间粒子群优化算法的优化结果明显比粒子群优化算法和改进粒子群优化算法的优化结果更小，即更经济环保。此外，50次独立计算各机组出力的统计优化结果如表3所示。

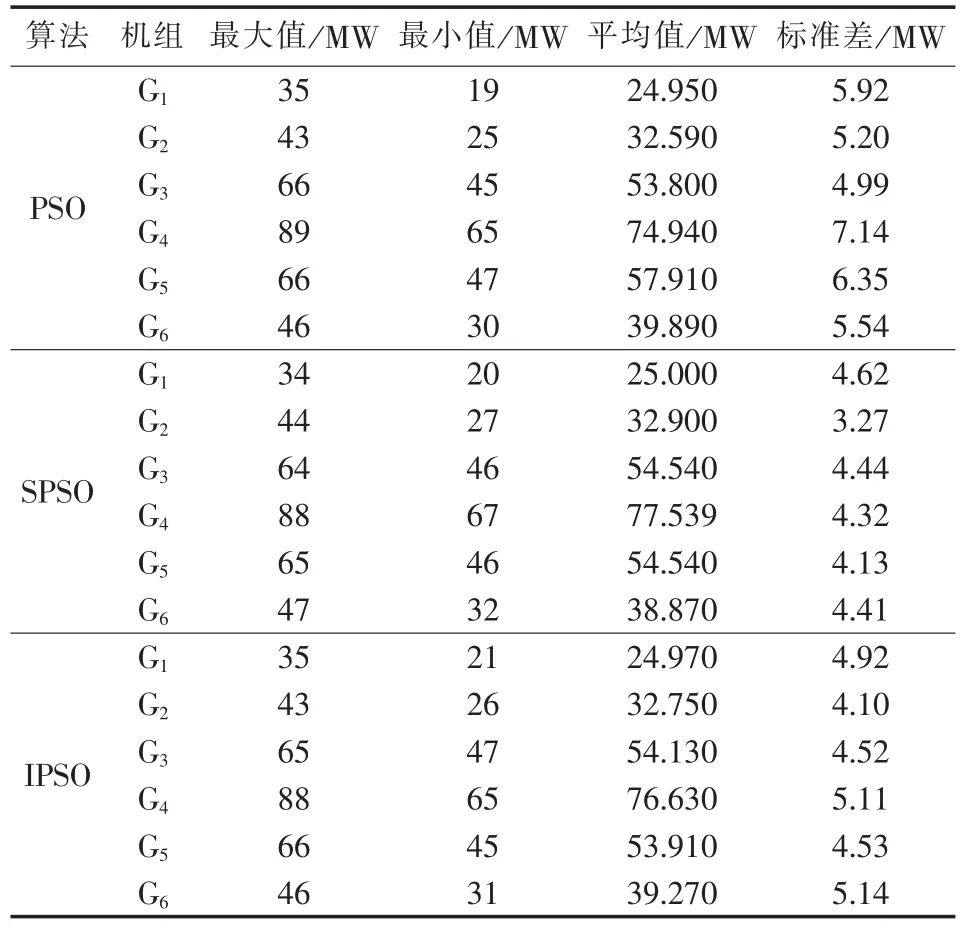
表3 机组出力优化结果Tab.3 Results of unit output power optimization

从表3中可以看出，空间粒子群优化算法所求得各发电出力优化结果的随机性也小于粒子群优化算法和改进粒子群优化算法的优化结果的随机性，这也进一步验证了空间粒子群优化算法优化结果较高的准确性。

为了体现空间粒子群优化算法在优化性能上的优势，选取了一次完成寻优过程的对比，三者的寻优过程如图2所示，图中适应度值为标幺值，后同。

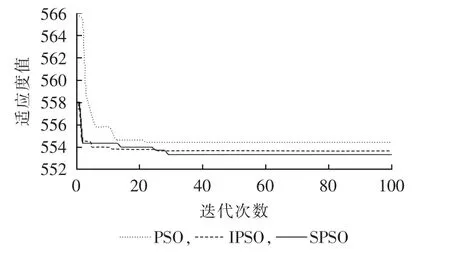
图2 不同算法收敛情况对比Fig.2 Comparison of convergence conditions by different algorithms

从图2中可以看出，空间粒子群优化算法在一定程度上比文献[4]中改进粒子群优化算法更好地缓解了粒子群优化算法容易陷入局部最优且难以跳出来、导致过早收敛的缺陷。从图2中可以看出，对于较为复杂的系统，空间粒子群优化算法对比改进粒子群优化算法和粒子群优化算法优势更加明显。在收敛性能方面，粒子群优化算法在迭代不到20次就陷入了局部最优而且不能自我调整跳出局部最优区域；改进粒子群优化算法虽然在前面部分跳出了局部最优区域，但是也在不到25次又陷入了新的局部最优；而空间粒子群优化算法出现了非常明显多次自我调整的现象，跳出局部最优区域，而且也在寻优不到30次就找到了全局最优解，获得了更好更精确的目标值，这也进一步展现了其良好的收敛特性和快速稳定的寻优性能，较好地解决粒子群优化算法容易陷入早熟且难以跳出局部最优区域的缺陷。

另外，图3给出独立计算50次情况下每次CPU所消耗的时间对比。从图3可见，空间粒子群优化算法虽然在粒子群优化算法的基础上增加高度参数，但对计算时间影响不大。在同等条件下，分别求得空间粒子群优化算法的CPU平均耗时为1.4702 s，改进粒子群优化算法的CPU平均耗时为2.4185 s，经典粒子群优化算法的CPU平均耗时为1.2623 s。文献[4]中空间粒子群优化算法最耗费时间，以牺牲计算时间来提高计算精度，而空间粒子群优化算法和粒子群优化算法仅相差0.2019 s，几乎不影响计算速度。通过算例分析结果表明：与改进粒子群优化算法相比，空间粒子群优化算法进一步增强了全局搜索能力，较好地改善了早熟的缺陷；其优化结果的随机性更小，提高了计算结果的可信性；尽管引入了高度参数，但对计算时间几乎没有影响。

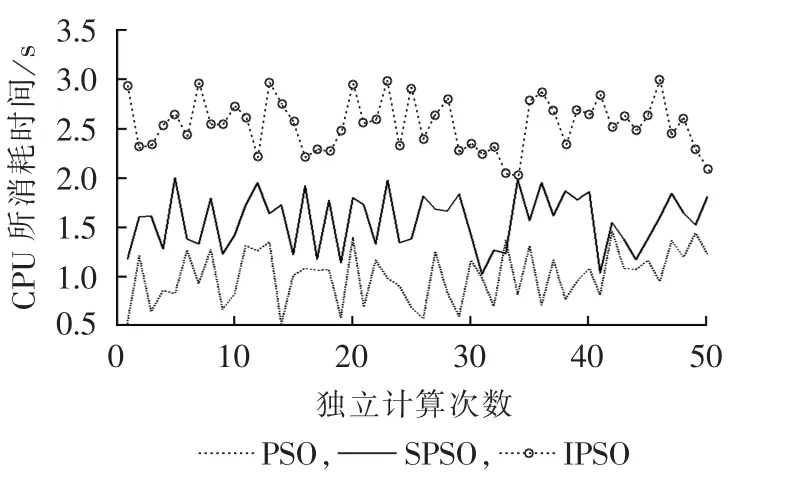
图3 计算时间对比Fig.3 Comparison of computation time

3.3 检测函数分析

为了进一步体现所提出的空间粒子群优化算法的优越性，选取了一个典型多峰值函数Rosenkbrock来进行测试，其函数具体表达式如下式所示：

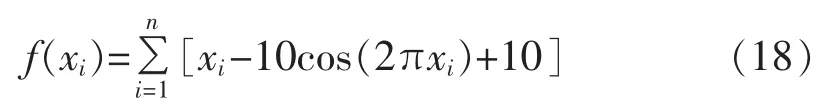
该函数在 xiє（－5.12，5.12）范围内大约存在 10n个局部最小值。针对以上测试函数初始化空间粒子群优化算法参数：粒子数m取40个；变量数n取20个；最大迭代次数取 1000 次；ωmax取 0.9；ωmin取 0.4。计算结果如图4所示。

图4 收敛情况对比Fig.4 Comparison of convergence condition

从图4中可以看出，对于含多峰值的优化问题，粒子群优化算法优化性能显著下降，过早陷入局部最优，导致很难找到全局最优解；改进粒子群优化算法虽然相比经典粒子群优化算法寻优性能有所改进，但是其最终寻优结果精确度不高；而空间粒子群优化算法寻优性能优势明显，仍然可以找到最优解，而且非常稳定趋向于最优解，可以找到更好的目标值，使得其寻优精度高。由此进一步体现了空间粒子群优化算法的优越性。

4 结论

针对经典粒子群优化算法容易陷入局部收敛而早熟的问题，本文提出了具备空间寻优能力的空间粒子群优化算法，并应用于求解电力系统环保经济负荷分配的问题，获得了满意结果。

空间粒子群优化算法通过引入一类高度参数，使粒子的移动由其高度和速度共同决定，对应的每个待优化变量由高度、速度和位置3类参数来寻优，粒子在一个新的具有高度维度的空间解域内搜寻。通过比较粒子当前适应度值与平均适应度值来决定高度的修正方式，提高了全局收敛性，增强了全局寻优能力，可以有效地跳出局部最优空间。

仿真结果表明，对比经典粒子群优化算法和改进粒子群优化算法，本文方法易于跳出早熟区间，并可极大减少计算结果的随机性；迭代次数并未显著增加，收敛时间相对较短，对优化变量的可微性要求不高。因此所提出的空间粒子群优化算法在解决非线性、非凸性、不连续的优化问题中同样具有有效性和优越性。