分布式电源对配网可靠性的影响及优化配置
2014-09-28宿晓岚谢开贵
赵 渊,何 媛,宿晓岚,谢开贵
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.重庆市电力公司市区供电分公司,重庆 400013)
0 引言
近年来,分布式电源(DG)技术因独有的环保性和经济性在全球范围内引起了人们越来越多的关注。DG具有减轻环境污染、降低终端用户费用、减少线路损耗、改善电能质量和提高配电网可靠性等特点[1-2],种类繁多的DG以不同方式、容量和位置接入配电网,改变了传统配电网的结构和运行方式,同时也对配电网可靠性评估带来显著影响。
目前,国内外众多学者都对DG接入配电网所带来的影响进行了多方面分析。其中关于DG的选址与定容却大部分集中于以提升系统经济性或降低网损为目标,鲜有文献将DG的优化配置与配电网可靠性评估相结合。文献[3-7]以网损最小为优化目标,分别采用蜂群算法[3]、启发式搜索法[4]、遗传算法[5]、改进粒子群算法[7]等进行求解。 文献[5]提出在降低网损的同时还需保证可接受的系统可靠性等级与电压质量,但其对配电网可靠性的考虑仅粗略体现于约束条件中。文献[6]将DG的选址与定容分开,先以等效网损微增率的排序结果确定DG安装位置,再通过考虑有功网损、电压和环境改善程度来确定最优容量。文献[8]以配电网年运行费用最小为目标,综合考虑电网网损费用、DG运行总费用以及购电费用,但没有评价DG的接入对配电网可靠性的影响。文献[9]虽基于电力不足概率对DG配置方案进行了可靠性评估,但其主要研究微电网内DG作备用电源时的优化配置,且将DG出力看作恒功率输出模型。
孤岛是随DG引入配电网后应运而生的一种新运行方式,它的存在使配电网故障恢复和可靠性评估变得更加复杂。文献[10]根据负荷的重要程度建立孤岛划分模型,采用改进的最小路法研究了恒功率DG并网对配电网可靠性的影响。文献[11-12]结合孤岛成功运行概率,分别采用多场景技术和风力发电机多状态模型对含风电DG的配电网进行可靠性评估,但都没有明确孤岛的划分策略。文献[10-12]认为计划孤岛一旦确定,对于任何故障情况其孤岛运行策略不再改变,使得孤岛运行不能很好地与当前实际运行状态相配合。文献[13]从确定风电的最大供电范围与供电次序来代替孤岛搜索,实现风电随机出力与其供电范围内供电可靠性指标的映射。
综上所述,本文从改善配电网供电可靠性角度出发,根据DG出力模型和配电网实际运行情况,将动态孤岛搜索与可靠性评估相结合,从而得到各负荷点与系统可靠性指标。在此基础上,为克服粒子群优化(PSO)算法所存在的早熟问题以及人工鱼群算法(AFSA)收敛速度过慢的缺陷,提出适用于DG优化配置的改进粒子人工鱼群混合优化算法。通过对IEEE-RBTS Bus6系统主馈线F4进行分析,验证了所提方法的有效性和正确性。
1 最优孤岛搜索
1.1 风力发电机的可靠性模型
风电具有保护环境、节约资源等特点,是目前可再生DG的一种重要形式,其大量接入将对配电网的可靠性评估产生重大影响。
风电的输出功率受风速影响而具有间歇性与随机性,因而不能简单地用两状态模型来描述其功率输出特性。图1描绘了风电机组的输出功率与风速之间的关系曲线。
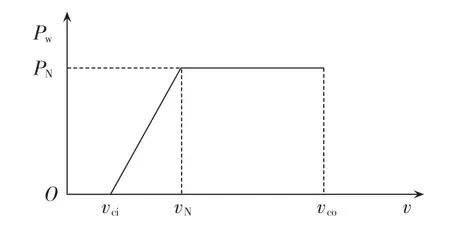
图1 风电机组功率特性曲线Fig.1 Characteristic curve of wind turbine generator output power
由图1可得到风电输出功率与风速之间的函数关系如下[11-13]:

其中,Pw、PN分别为风力发电机的输出功率、额定功率;vci、vN、vco分别为切入风速、额定风速、切出风速。
本文以小时平均风速代替实时风速,采用文献[14]中的小时风速及持续时间数据。风力发电机的切入风速为 4m/s,额定风速为 14m/s,切出风速为 25m/s。结合式(1)可将风力发电机划分为S个出力状态,其不同输出功率水平及所对应的概率值如表1所示。

表1 风电机组输出功率的概率分布Tab.1 Probability distribution of wind turbine generator output power
1.2 结合配电网运行实际确定孤岛划分
DG接入配电网的方式主要分为通过变电站母线接入和通过馈线接入[15]。通常情况下配电网母线被视为无限大电源,因此,从可靠性角度出发,本文讨论DG通过馈线接入的情况。
在配电网接入DG的位置与额定容量确定的情况下进行最优孤岛划分,需要考虑故障发生的位置和DG的出力状态模型。本文对文献[15]所提出的启发式孤岛搜索方法加以改进,使之适用于以提高配电网可靠性为目的的DG优化配置。
首先确定孤岛划分的两大原则:在岛内负荷不超过DG总出力的前提下尽可能包含多的负荷;尽可能包含负荷等级高的负荷[15-16]。下面给出最优孤岛搜索的算法步骤。
(1)本文假设配电网中每条馈线都可接入DG,在每条馈线段上装设分段装置,馈线段数目为n。通过网络化简,以馈线两端的断路器和隔离开关为端点,将配电网分为n个馈线单元,每个单元都为DG配置的候选地址。 各单元按其功率值 Pa(a=1,2,…,n),分为正单元、负单元以及零单元,其中正单元(Pa>0)代表该单元对外输出功率,负单元(Pa<0)代表该单元消耗功率,零单元(Pa=0)代表该单元既不输出也不消耗功率。将负荷功率设为负值,DG功率设为正值。图2为一简单的单元划分示例,其中单元1、4、5、6为负单元,单元2为零单元,单元3的功率值则由负荷和DG输出功率共同决定。

图2 单元划分示例Fig.2 Example of cell division
(2)形成单元联接矩阵A。对于原配电网(DG没有接入),针对n个馈线单元形成n维单元联接矩阵A(n×n维),Ai,j=1(i,j=1,2,…,n;i≠j)表示单元 i与 j相邻,Ai,j=0(i≠j)表示不相邻,令 Ai,j=0(i=j)。 记录各个单元的单元特征,即功率值大小Pk和负荷等级(分为一、二、三类负荷,一类负荷为最重要的负荷)。当单元 f(f=1,2,…,n)发生故障并引起其邻近的隔离开关或断路器动作时,配电网结构发生改变,则令矩阵A中第f行和f列元素都为0,得到新的单元联接矩阵A,其每一行代表了此单元与其余单元的邻接关系。
(3)考虑DG的接入,修改各单元的功率值。DG接入个数为 m,额定功率为 PDGt(t=1,2,…,m),接入的单元编号为ncellt。本文认为所研究的配电网区域在同一时刻风速相同,因此可按照表1得到状态s(s=1,2,…,S)出现的概率 ps,以及该状态下各风力发电机的输出功率水平 PDGt,s。 将第 ncellt(ncellt≠ f)个单元的功率值改为在原基础上加上PDGt,s,得到在状态s下的新功率值向量 Ps=(P1,P2,…,Pn)。
(4)搜索在状态s下的孤岛划分方案,步骤如下。
a.对于每个正单元,其满足本地负荷需求,都可各自形成最初的孤岛。设某一正单元的单元编号为k(k=1,2,…,n),对其执行孤岛扩大操作。在矩阵 A第k行中找到其单元邻接表,若相邻单元中含正/零单元g,立刻将其融入;若只有负单元,则查看其是否满足单元k的供电能力。如果所有相邻单元都在k的供电能力外,则孤岛不再继续扩大;否则,将其中负荷等级最高的单元g融入,合并成为一个新的单元。新单元包含了原单元k和g这2块区域,其功率值更新为Pk+Pg(Pk+Pg≥0)。单元联接矩阵A也相应改变:融合前所有与k或g相邻的单元(除去k和g本身)成为融合后新单元相邻的单元,而之前相邻于k或g的单元,都修改为与新单元相邻。具体操作为:①将矩阵A第g行所有元素对应相加到第k行,在新的第k行元素中,若存在大于1的值,将其置1,并将该行中第k和g个元素值置零,同时令第g行所有元素为零;②若存在 Ai,g=1(i=1,2,…,n)的元素,则修改为 Ai,g=0,Ai,k=1。以图 2 为例,假设单元 1 发生故障,矩阵A中第1行和第1列都置零,单元2和3融合,则:

新矩阵A仍然为n×n维矩阵,原单元2和3合二为一成为新的单元2,其余单元编号不变。该方法可减少计算复杂度,方便以下步骤继续执行。
b.按照步骤a的方法对孤岛继续扩大,直到不能扩大且遍历所有正单元为止。得到初步孤岛划分结果。
c.继续查找是否有同时邻接至少2个初步孤岛的负单元,如果有,则找出满足邻接孤岛联合供电能力的单元,并将其中负荷等级最高的单元融入。接着以类似步骤a的方法修改新孤岛单元的功率值和单元联接矩阵A,若其仍具有继续扩大的能力,则返回上述步骤继续执行直到各孤岛单元都不再融合为止,由此得到状态s下的最终孤岛划分方案,记为一次完整孤岛搜索。
对于同一单元故障分别按照S个风力发电机出力状态作S次完整孤岛搜索,记录下该单元故障时的S种孤岛划分方案以及每一种对应方案发生的概率ps,为配电网可靠性评估做好铺垫。
2 结合孤岛搜索对配电网作可靠性评估
按照1.2节的单元划分对含风力发电机的配电网进行可靠性评估,风力发电机通过断路器接口接入配电网。通常情况下仅考虑单阶元件故障,且在故障修复期内不会出现新的元件故障。
为得到各负荷点可靠性指标的解析计算模型,首先进行网络化简,求取各馈线单元的等效故障率。馈线单元由变压器、负荷支路、熔断器、馈线段、断路器以及全部或部分DG组成。将馈线单元的等效故障率分为对外影响和对内影响,对外影响的等效故障率为:
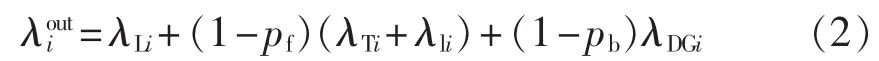
对内影响即表示该单元内元件发生故障时对该负荷支路线上的负荷点的可靠性影响,即:

其中,λouti和λini分别为第i个馈线单元对外和对内影响的等效故障率;λLi、λTi、λli、λDGi分别为该单元内馈线段、变压器、负荷支路线以及DG的故障率;pf和pb分别为熔断器和断路器可靠工作的概率。若单元内缺少某些元件,将其对应参数设置为0即可。
配电网加入DG后与传统配电网的最大区别在于故障恢复时间的不同,即故障所引起的负荷点停运时间发生改变。本文将可靠性计算的最小路法与故障后最优孤岛搜索相结合。首先求取每个负荷点到母线电源的最小路,将所有单元分为最小路上的单元与非最小路上的单元。
将负荷点j作为研究对象,其最小路上的单元故障都会引起负荷点j停运,停运时间依赖于系统的结构、故障单元的位置以及DG的配置与出力状态。设故障单元q为其最小路上的单元,启动第1节的孤岛搜索程序,得到S个状态下的S种孤岛划分方案及对应概率ps,统计负荷点j位于孤岛内的概率pisland,由此得到该负荷点在单元q故障时的停运时间rjq为:

其中,t1=max{V,T},代表负荷点 j位于孤岛内,V 为分段装置的操作时间,T为孤岛形成需要的倒闸操作时间;t2为故障单元的平均修复时间,代表负荷点j不在孤岛内。
当负荷点j非最小路上的单元发生故障,可根据系统结构,将其对负荷点可靠性指标的影响折算到相应的最小路单元上进行处理,不再赘述。
应用上述方法结合网络法中串联等值原理即可求得各负荷点的等值故障率λj、故障修复时间rj以及年停电时间Uj。则系统的电量不足指标为:

其中,Lj为第j个负荷点的平均负荷。该指标即可作为DG定容与选址的目标函数。
另外,为提高配电网重要负荷的供电可靠性,本文提出带负荷权重的系统可靠性指标为:

其中,wj代表了负荷的重要程度,其值越大,该负荷越重要。
3 基于配电网可靠性的DG优化配置
3.1 DG优化配置的数学模型
本文以提升配电网供电可靠性为目标,对DG的选址与定容进行优化。
首先需要建立DG优化配置的数学模型,根据需要,目标函数可取为式(5)或式(6)。由于DG的加入会对配电网的运行、同步和稳定等方面产生一定的影响,因此DG的定容需考虑到系统所能接受的最大穿透功率限制[5,17],即根据实际需要和电网发展情况限制DG所允许接入的总容量。
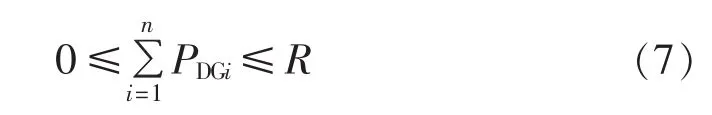
其中,n为可安装DG的候选节点个数;PDGi为节点i实际接入的DG容量;R为系统中DG所允许接入的总容量,其可由最大穿透功率限制进行确定。
待选节点DG安装容量约束为:

接入DG个数约束为:

其中,Ri为节点i允许安装的DG最大容量;m、M分别为DG实际接入个数和允许安装的最大个数。Ri和M的大小可根据实际需要和电网发展情况进行确定。 其中参数 n、Ri、R、M 为事先已知量,PDGi、m 值即为该优化模型的DG优化配置结果。
此外,还可加入系统潮流约束、节点电压约束、线路容量约束等。
将上述模型的不等式约束以惩罚因子的形式并入到归一化目标函数中,作为优化计算的适应度函数。
3.2 粒子人工鱼群混合优化算法的DG优化配置
粒子群和人工鱼群算法的原理介绍可参照文献[18-19],本文不再赘述。利用粒子群算法的快速局部搜索和人工鱼群的全局收敛性,通过相互跟踪最优解,实现种群间的信息共享,可有效应用于求解以提升配电网可靠性为目标的DG优化配置。
对于状态变量的编码,最简单的方法是以可安装DG的候选节点数n为变量维数,即X=(x1,x2,…,xn),xi(i=1,2,…,n)的值表示节点 i所接入的 DG 容量,xi=0则代表节点不安装DG。然而,当n值较大时,这样的变量设置会导致计算量过大且不易获得最
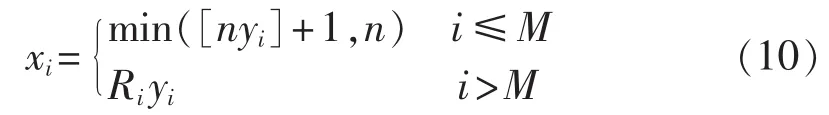
其中,[nyi]表示不大于nyi的最大整数。若存在xi=0,即意味着实际接入配电网中的DG个数m小于允许安装的最大个数M。
将粒子群与人工鱼群有效结合,虽然可在一定程度上增强全局收敛性,提高计算速度,但在非全局极值点出现较严重的聚集情况时,其收敛速度将大幅减缓,甚至再次陷入局部最优。因此,本文通过适时添加变异操作,引导种群寻优计算的同时保持个体多样性,使之适用于配网中的DG选址与定容优化。其计算步骤如下。
a.初始化。确定种群规模N,在变量可行域内随机生成N个个体,设置算法基本参数惯性权值ωmax和ωmin、学习因子 c1和 c2、位置限值 xmax和 xmin、速度限制vmax和 vmin、视野范围 Fvisual、移动步长 δstep、拥挤度因子δ、试探次数 nt、最大迭代次数 nitermax,以及 Ri、R、M、惩罚因子和变异概率p等。优化变量按上述策略进行编码。计算每个个体的适应度函数值,取最优值及相应的DG配置策略赋值给公告板,初始gbest(整个粒子群的历史最优位置)也取为该公告板上的配置方案。
b.粒子人工鱼群算法。把种群均分为2个种群pop1、pop2。在每次迭代中,将pop1按粒子群算法操作,得到pbest(个体粒子的历史最优位置)、gbest及新的种群pop*1;pop2按人工鱼群算法操作,得到最优解u及新的种群pop*2。为加强2个种群间的信息交流,提高计算效率,将gbest、u以及原公告板上的数值进行比较,取最优解赋值于新的公告板,同时,也更新gbest为该公告板上的解,为下一次迭代做好准备。
c.根据具体情况选择变异。若公告板在连续2优解。通常情况下,配电网中接入DG的最大个数M远小于可安装DG的候选节点数n,X中大部分变量值为0。因此,为了减少状态变量维数,提高计算效率,本文将粒子群优化算法中每个粒子的个体状态和人工鱼群算法中每条人工鱼的个体状态均定义为向量 X=(x1,x2,…,xM,x1+M,x2+M,…,x2M),其中 xi(i=1,2,…,2M)为欲寻优的变量,X中前M个变量代表DG的安装地址,后M个变量即为对应的安装容量(安装地址 xi对应容量 xi+M(i=1,2,…,M)。
需要注意的是,状态变量X中前M个变量为整数变量,其取值范围为[1,n];而后M个变量则为实数变量,取值范围为[0,Ri](i=1,2,…,M)。 为减少计算复杂度,本文将X中所有变量转换为相同取值范围内的实数。具体操作为:
2M 个变量 y1、y2、…、yM、y1+M、y2+M、…、y2M均属于[0,1]区间内的实数,xi与 yi(i=1,2,…,2M)对应。则有:次迭代过程中没有改变或变化极小,为防止陷入局部最优,采用增加随机扰动的方法对其进行变异操作,即 gbest=gbest+0.5rands(1,2M),其中 rands(1,2M)为(-1,1)内的随机数向量。计算适应度函数值并与原公告板进行比较,若优则变异成功,更新公告板和gbest;否则,重新变异,直到变异成功或达到预置的最大尝试次数为止。
d.变异操作。为提高计算效率,在每一次迭代结束时,从pop*1与pop*2中选出适应度最差的N/10个个体,每个个体产生一个随机数 rand є(0,1)。 若rand<p,该个体变异,Xi=Xi+0.5rands(1,2M),其中Xi为被选中的个体。注意,在以上步骤中,当个体内某一变量或多个变量值越限,则将该变量置为相应的边界值,使变量限制于[xmin,xmax]内。
e.判断迭代次数niter是否达到预置的最大迭代次数nitermax,若是则转向步骤f,否则继续进行下一次优化迭代。
f.算法终止,输出最优解(即公告板中的DG配置方案)。
算法流程如图3所示。

图3 求解DG优化配置的流程图Fig.3 Flowchart of optimal DG allocation
4 算例分析
本文采用IEEE-RBTS Bus6系统主馈线F4作为测试系统进行DG的布点规划,见图4。该系统包括25条馈线段,5条负荷支路线,21个隔离开关,4个断路器,23个负荷点及配电变压器、熔断器。设断路器和熔断器 100%可靠动作,max{V,T}取为 0.5 h。各元件及负荷点的原始数据见表2—4,一、二、三类负荷的单位权重分别取100、10、1。
粒子人工鱼群混合优化算法的参数选取如下:c1=c2=2,ωmax=0.9,ωmin=0.4,由于所有变量都转化为[0,1]区间内的实数,则取 xmax=1、xmin=0,vmax=-vmin=1;可视域Fvisual=2,移动步长δstep=0.3,拥挤度因子δ=0.618,nt为 30次;惩罚因子取 1 000,变异概率 p=0.1,种群规模N取60,最大迭代次数为100。
由1.2节单元划分方法可将图4的配电网测试系统划分为25个馈线单元,其单元编号1—25如图4所示,每个单元都可接入DG,即n=25。以下从配电网无DG接入、接入DG类型为风力发电机、接入恒功率输出DG几个方面来讨论DG的优化配置对配电网可靠性的影响。

图4 配电网测试系统Fig.4 Distribution network test system

表2 元件可靠性参数Tab.2 Reliability parameters of components
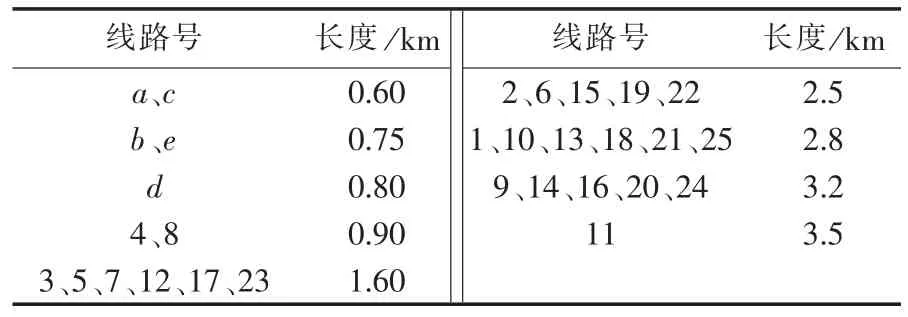
表3 线路参数Tab.3 Parameters of lines
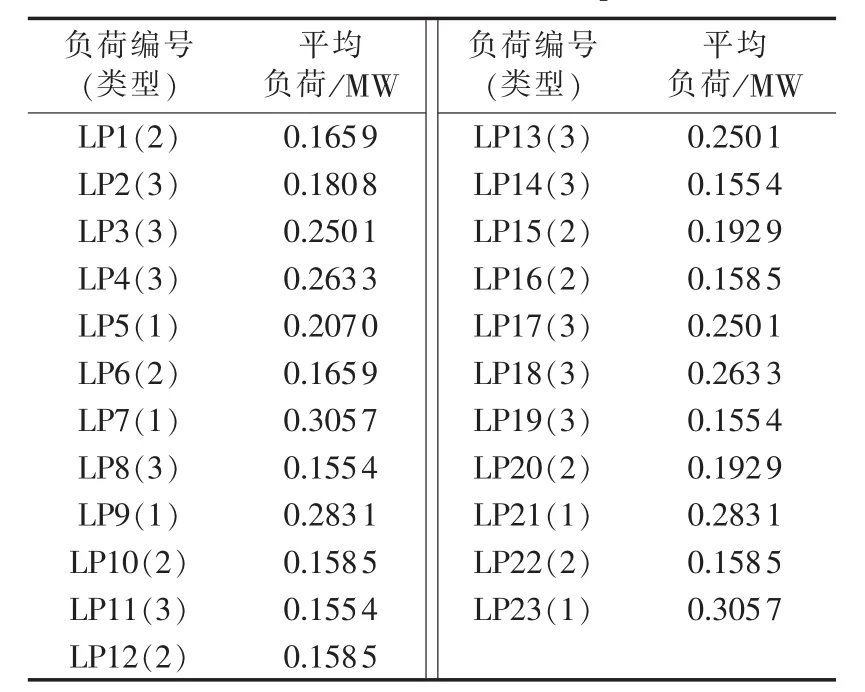
表4 负荷点参数Tab.4 Parameters of load point
Case1:配电网无DG接入,计算得到系统可靠性指标 ENSI=50.0795 MW·h/a,ENSIw=1690.6024 MW·h/a。由于篇幅限制,本文仅列出一类负荷点的可靠性指标如表5所示。
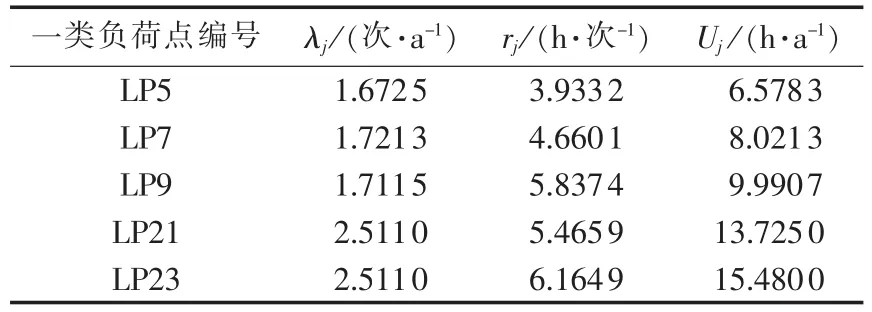
表5 无DG时的负荷点可靠性指标Tab.5 Reliability indexes of load points without DG
由表5可知,在无DG接入时,越靠近配电网末端的负荷点其可靠性越差。
Case2:DG类型为风力发电机,待选单个风力发电机的额定容量为 C×100 kW(C=1,2,…,10),各节点允许安装的最大容量Ri=1 MW,系统允许接入的风力发电机总容量R=2 MW,可安装数目M=3。
目标函数采用式(6),利用本文模型与方法得到的风力发电机优化配置结果如表6所示。表7给出了该配置方案下的一类负荷点可靠性指标。
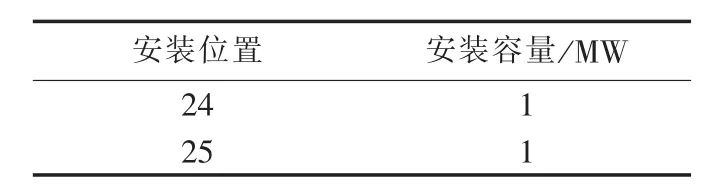
表6 风电机组最优配置方案Tab.6 Optimal allocation scheme of wind turbine generators

表7 配置风电机组后的负荷点可靠性指标Tab.7 Reliability indexes of load points with wind turbine generators
目标函数值 ENSIw=1388.9534 MW·h/a,系统的电量不足指标ENSI=45.1856 MW·h/a。与Case1相比,配置风力发电机后各负荷点以及系统的可靠性水平都得到了提升,尤其对配电网中末端的重要负荷,其可靠性改善效果更加明显。由表6可知,风力发电机的安装位置靠近配电网末端,且位于重要负荷附近。
Case3:接入恒功率输出的DG,其余条件与Case2相同。该DG采用两状态模型,可用率取为0.98,以式(6)为目标函数,得到DG优化配置结果如表8所示。表9给出了该方案下的一类负荷点可靠性指标。

表8 DG最优配置方案Tab.8 Optimal allocation scheme of DGs
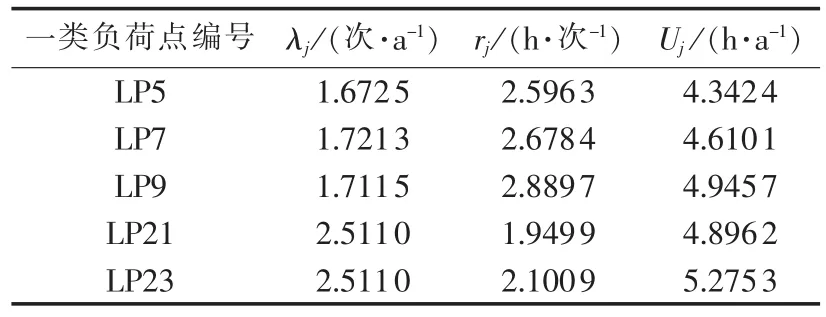
表9 配置DG后的负荷点可靠性指标Tab.9 Reliability indexes of load points with DGs
目标函数值 ENSIw=797.4481 MW·h/a,系统的电量不足指标ENSI=37.3471 MW·h/a。优化结果表明,恒功率输出DG安装于配电网中末端,仍聚集在重要负荷附近。且相比于配置总容量相同的风力发电机,该方案的可靠性改善效果更好。由此可见,若DG能够保持稳定的功率输出,尽量克服风力发电机输出功率的随机性与间歇性,配电网便能获得更高的可靠性水平。
Case4:接入恒功率输出的 DG,以式(5)为目标函数进行DG的选址与定容,其计算结果如表10、11所示。
系统可靠性指标 ENSIw=1079.3941 MW·h/a,ENSI=34.0592 MW·h/a。目标函数不同,配置方案与可靠性指标也不尽相同。该方案虽可以获得更好的系统电量不足指标,但其对重要负荷(如LP5、LP7、LP9)的可靠性改善效果不明显。因此,该算例也从侧面说明了不同的负荷重要程度和负荷分布会导致不同的DG优化配置方案和配电网可靠性水平。
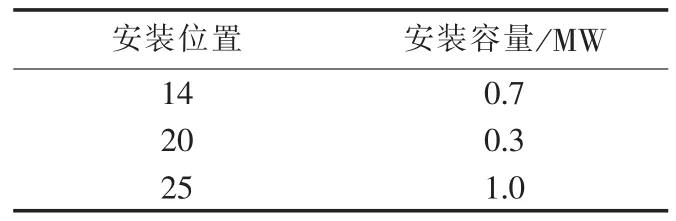
表10 基于ENSI的DG最优配置方案Tab.10 Optimal DG allocation scheme based on ENSI
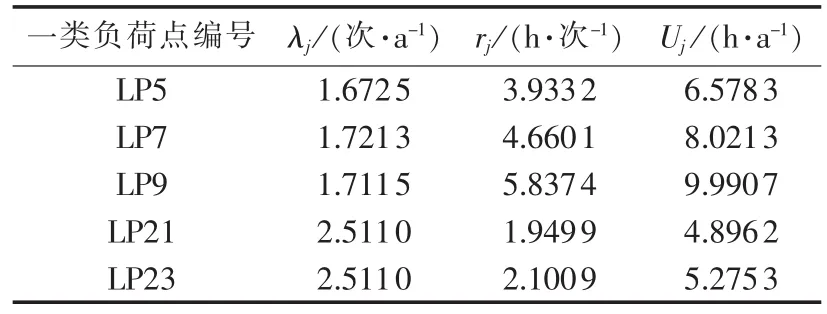
表11 负荷点可靠性指标Tab.11 Reliability indexes of load points
图5为以ENSIw为目标函数,分别采用改进的粒子人工鱼群算法、自适应粒子群算法以及人工鱼群算法对Case3作DG优化配置的迭代曲线图。从图5可以看出,粒子群优化算法由于缺乏适当的引导容易陷入局部最优,出现早熟现象;人工鱼群算法相比粒子群优化算法能更好地搜索最优解,但运行效率较低,且搜索精度不高;本文所提方法集合了粒子群优化算法与人工鱼群算法两者的优点,并引入变异操作,具有较快的收敛速度和良好的精度。

图5 为DG优化配置采用不同优化算法的迭代曲线对比图Fig.5 Comparison of iteration curve among different DG allocation optimization algorithms
5 结论
本文从改善配电网供电可靠性的角度出发,根据配电网运行实际和风力发电机出力模型动态地生成故障后孤岛方案,并与配电网可靠性评估相结合。采用改进粒子人工鱼群混合优化算法,以带负荷权重的系统可靠性指标ENSIw为目标函数分析DG的选址与定容。仿真结果得到以下结论。
a.DG的安装位置位于配电网中末端,且与配电网的负荷分布、负荷重要程度以及DG类型密切相关。
b.改进粒子人工鱼群混合算法增强了个体间的信息交流,粒子群优化算法与人工鱼群算法相互取长补短,通过适当的变异操作,有效地提高了寻优效率。
c.通过对有无DG接入的配电网可靠性计算结果进行比较可知,DG的接入提高了系统可靠性,尤其对重要负荷的可靠性改善效果明显。因此,合理地接入DG对提高配电网的供电可靠性具有重大意义。
另外,Case2和Case3的仿真结果比较表明,在系统所允许接入DG总容量和其他约束条件相同的情况下,相比于优化配置具有间歇性和随机性的风力发电机,配置恒功率输出DG能够给配电网带来更好的可靠性性能。因此,在配置新能源DG时可以适当配合储能设备或其他策略,稳定功率输出,进一步提升配电网可靠性的同时还能降低系统成本,提高环保性能。
