基于改进参数检测法的双端非同步数据故障测距算法

高厚磊，陈学伟，刘洪正，李 超，冯迎春

（1.山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061；2.国网冀北电力有限公司唐山供电公司，河北 唐山 063000；3.国网山东省电力公司检修公司，山东 济南 250021）

0 引言

高压输电线路的准确故障测距是从技术上保证电网安全经济运行的重要措施之一。输电线路的测距方法按所采用的信息量可分为单端法、双端法和多端法等。单端测距法原理简单、投资少、不受通信条件的限制，但难以克服对端系统阻抗变化和过渡电阻的影响。双端测距方法不存在原理误差，能有效克服过渡电阻和对端系统阻抗变化对定位精度的影响。在双端算法中，基于两端同步数据的测距算法较为简单，但实现时需要GPS同步时钟的安装并获取可靠的同步效果，目前除PMU装置外还很难有其他设备满足要求。超高压输电系统的故障录波装置已经联网，但数据不具备测距所要求的同步条件。因此，不需要两端数据同步的双端测距算法更具必要性，具有更大的工程实用价值[1-3]。

基于线路双端非同步数据的故障测距算法主要有参数检测法、电压趋势法、拟牛顿迭代法等。文献[4]提出的参数检测法虽然能修正线路参数，但其对双端非同步角度的修正是基于线路投运初期的数据，对于长期运行的输电线路误差不可避免。文献[5-6]提出的电压趋势法是基于线路两端的电压和电流所计算出的故障点的电压幅值相等的假设建立方程求解，即使不考虑求解超越方程所用算法（遗传算法、迭代搜索法等）的复杂性，此类方法还需要证明在全线路上有且仅有一个点满足电压幅值相等的条件。文献[7-10]提出的拟牛顿法、参数估计法等都是基于求解非线性方程组的迭代方法，算法实现相对复杂，计算量大。此外，以上文献中都没有对输电线路不完全换位对测距的影响作出分析。

本文在以上工作的基础上，基于输电线路分布参数模型，提出了基于改进参数检测法的双端非同步数据故障测距算法。该算法利用故障前两端电压电流数据实时修正不同步角度，同时修正线路参数，再利用故障后数据进行故障测距，在线路不完全换位的情况下也能得到较为准确的测距结果。与拟牛顿法、参数估计法等相比，本文算法无需迭代、计算量小；与电压趋势法相比，本文算法不存在伪根判别的问题；与传统参数检测法相比，本文算法能实时修正非同步角度。

1 输电线路分布参数模型及误差归算

1.1 分布参数模型

图1所示为均匀输电线路的分布参数模型，z1、y1分别为单位长度线路的阻抗和导纳。

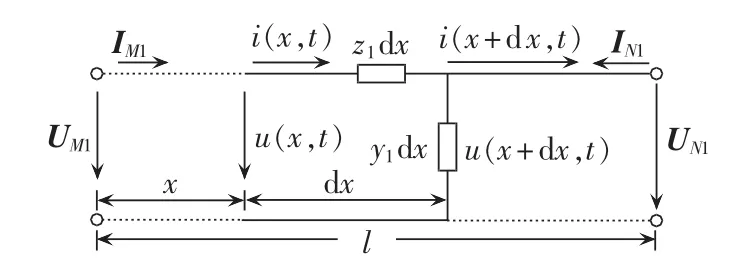
图1 输电线路分布参数模型Fig.1 Distributed parameter model of power transmission line

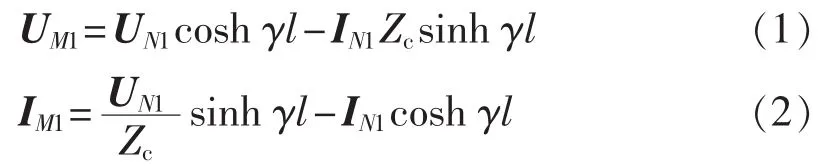
其中，UM1、IM1分别为稳态运行时M端电压、电流的正序分量；UN1、IN1分别为稳态运行时N端电压、电流的正序分量；γ为线路传播系数；Zc为线路特性阻抗；l为线路全长。

1.2 参数误差归算

即使采用分布参数输电线路模型，与实际线路当

由图1所示的电压、电流相量和线路分布参数，可以得到均匀长线传输方程[11-15]：前参数相比也会存在一定的误差。为提高测距精度，需要修正各类误差，这些误差包括线路阻抗的误差、线路长度的误差、线路不完全换位造成的误差以及测量误差等。

首先以线路长度的变化与线路参数之间的关系为例进行分析。若已知线路的给定长度为l，线路的实际长度为l+Δx，线路单位长度的正序阻抗和导纳分别为Z1和Y1。在此，不妨假设线路阻抗和导纳与线路长度近似呈线性关系，在进行故障测距时，如果仍然按照线路长度为l来计算，则相当于线路单位长度的正序阻抗和导纳分别增加了Δx/l×100%，变为Z′1=（1+Δx/l）Z1和Y′1=（1+Δx /l）Y1。 因此，线路的等效传播系数和等效特性阻抗变为：

其中，γ、Zc分别为由线路给定参数计算而得的传播系数和特性阻抗。由式（3）可知，线路的等效传播系数 γ′变为 γ 的（1+Δx/l）×100%，而等效特性阻抗 Z′c和Zc相同。

由以上分析可知，线路的长度误差能够分摊到单位长度线路上，归化为单位长度阻抗和导纳的误差。此外，线路不完全换位造成的误差及测量误差等因素也是通过对线路参数的影响而反映在测距结果上的。因此可作假设，认为它们对测距的影响也可以归化到单位长度线路参数的变化上，并且对单位长度阻抗与导纳值的影响反映在数值上是近似同比例的。

不妨定义以上所有对测距结果产生影响的误差总和为误差归算系数α，则有：

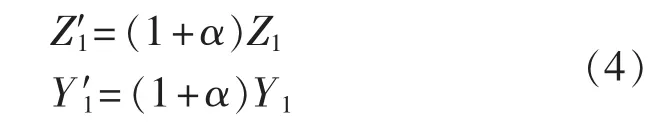
其中，Z′1、Y′1分别为误差归算后线路单位长度的等效正序阻抗和导纳。

由式（4）可以得：

由式（5）可知，线路的等效传播系数γ′变为原来的1+α倍，而等效特性阻抗Z′c保持不变。

2 双端非同步数据故障测距原理

双端供电系统如图2所示。在线路正常运行时，可由N端的电压、电流相量来表示M端的电压、电流相量，即式（1）、（2）所示的基于输电线路分布参数的传输线方程。

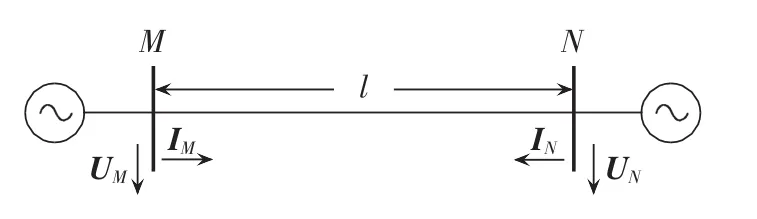
图2 双端供电系统示意图Fig.2 Schematic diagram of two-terminal power supply system

当两端电压、电流数据不同步时，设不同步角度为δ，并且计及线路参数误差的影响，则有：

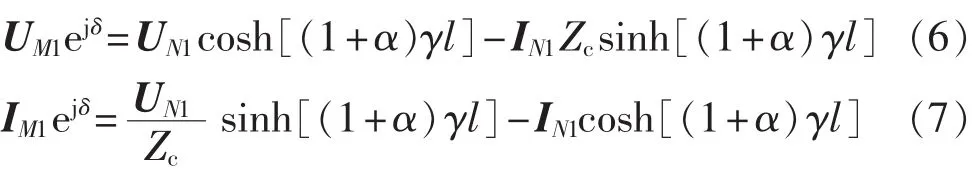
其中，未知量为误差归算系数α和非同步角度δ。

联立式（6）、（7）可得误差归算系数的解析解为：

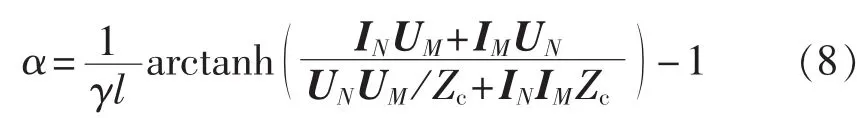
将由式（8）求得的α代入式（6）中，可以求得两端非同步角度为：

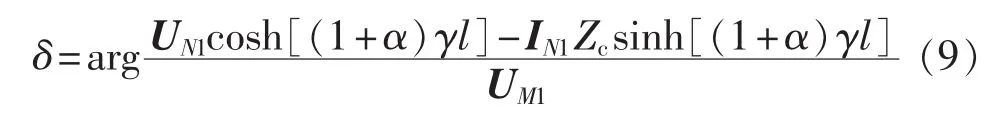
输电线路故障示意图如图3所示。故障点F与M端母线距离为x，与N端母线距离为l-x。

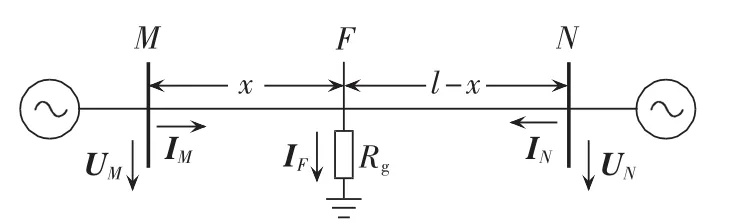
图3 输电线路故障示意图Fig.3 Schematic diagram of transmission line fault

F点发生故障后，若以线路M、N端的电压、电流作为已知条件，可以分别推出以两端电压、电流数据表示的线路故障点F处的电压方程：

其中，UMF、UNF分别为由M、N端电压、电流正序分量算得的故障点电压正序分量，故有UMF=UNF。

因此可得：

将 cosh x= （eγx+e-γx）/2 和 sinhx= （eγx－e-γx）/2 代入上式，计算可得：

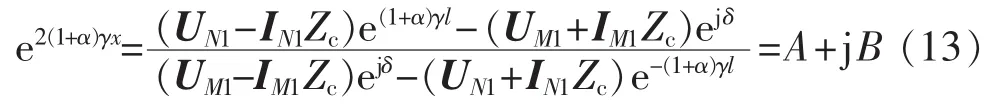
令（1+α）γ=m+jn，由于等式两端均为复数，为简化计算，可由式（13）两端复数的相角相等列式为2nx=arctan（B/A），进而可得故障距离：

由上述推导过程可知，所谓改进的参数检测法，即先根据式（8）、（9）由故障前数据求出当前误差归算系数α和两端非同步角度δ，再将其代入式（13）、（14）中，由故障后数据求出故障距离x。该方法是在同时考虑了输电线路当前两端非同步角度和线路参数误差的前提下进行故障测距，在理论上保证测距的准确性。

3 仿真验证及分析

3.1 仿真模型及改进参数检测法测距流程

在PSCAD中搭建的仿真模型及参数如图4所示。系统电压等级500 kV，线路全长300 km，采用分布参数线路模型，其中，ZM1、ZM0和 ZN1、ZN0分别为 M 端和N端的正序、零序系统阻抗；Z1、Z0分别为单位线路长度的正序、零序阻抗。在仿真过程中，针对不同故障类型在不同过渡电阻、不同故障距离、不同非同步角度、不同参数变化和不同负荷时的情况进行仿真计算和分析。

图4 仿真模型及参数Fig.4 Simulation model and parameters

具体测距流程如下。

a.取故障前一周期数据和故障后一周期数据，利用全波傅氏算法计算故障前后线路两端电压、电流的基频分量，再运用对称分量法求得电压、电流的正序分量。

b.根据式（8）、（9）利用故障前两端电压、电流的正序分量计算非同步角度δ和误差归算系数α。

c.将步骤b中求得的非同步角度δ和误差归算系数α代入式（13）中进行参数修正，利用故障后的两端电压、电流正序分量计算参数A和B，最后根据式（14）计算故障距离。

3.2 改进参数检测法与电压趋势法仿真结果对比

解决两端数据不同步问题的另一种测距算法为电压趋势法，当两端电压、电流数据不同步时，这种不同步只影响正弦信号的相位，而不影响其幅值。因此，利用两端数据测得的故障点F处的电压幅值相等，可得：

利用折半查找法求解式（15）即可得到故障距离x。电压趋势法是基于在发生故障时全线路上有且仅有一个点满足电压幅值相等的假设，即要求线路始末两端感受到的电压趋势呈单调变化。实质上，由线路两端数据算得的故障点电压幅值曲线可能是非单调的。

表1所示为在过渡电阻为100 Ω、两端电源相角差为20°、非同步角度为18°的条件下，不同故障类型、不同故障距离时改进参数检测法与沿线电压趋势法的测距结果对比。其中，测距误差的定义式为：

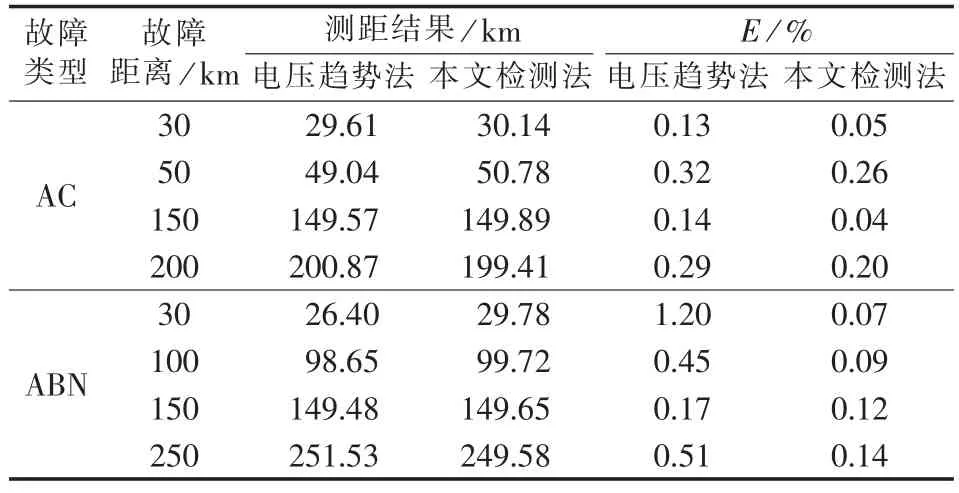
表1 改进参数检测法与电压趋势法测距结果对比Tab.1 Comparison of fault location results between proposed algorithm and voltage trend method

由表1可以看出，除电压趋势法在距离M端母线30 km处发生AB两相短路接地故障的测距结果外，2种基于非同步数据的测距算法误差都小于0.5%，但基于参数检测的故障测距算法精度更高。

为了更直观地进行对比分析，选取距离M端母线200 km处发生AC相间短路故障和距离M端母线30 km处发生AB两相短路接地故障的2组数据，应用电压趋势法绘制两端电压变化曲线如图5所示，应用改进参数检测法绘制测距动态特性曲线如图6所示（图6中，t=0 s时故障发生）。

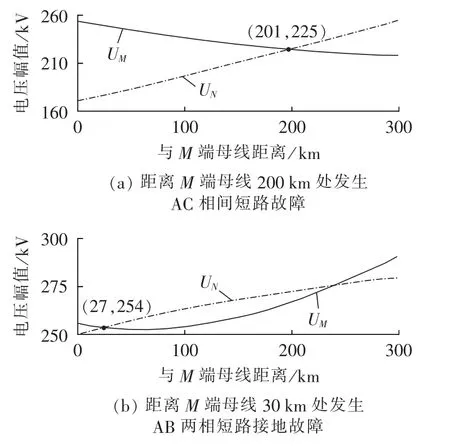
图5 电压趋势法测距结果Fig.5 Results of fault location by voltage trend method

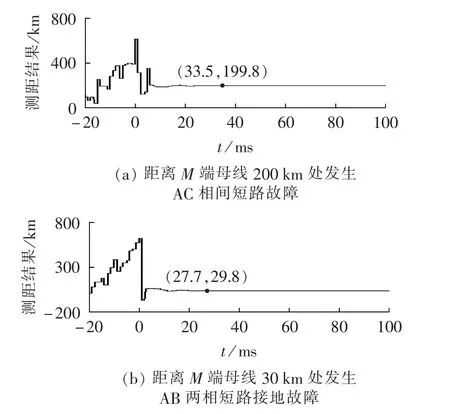
图6 改进参数检测法测距结果Fig.6 Results of fault location by proposed algorithm

由图5（a）可以看出，由M端、N端推得的故障后沿线电压趋势都是单调的，只有1个交点，测距结果准确；而在图5（b）中，由M端推得的电压幅值先减小后增大，与N端推得的电压幅值曲线有2个交点，不仅产生了伪根判别问题，对测距精度也产生了较大影响。 由图6（a）、（b）可以看出，改进的参数检测法在故障发生1个周期后即可获得较为准确的测距结果，并且不会产生伪根识别问题，在精度和可靠性方面都优于电压趋势法。

3.3 改进参数检测法在不同条件下的测距结果

表2所示为不同过渡电阻及不同负荷条件下，改进参数检测法的测距结果，其他参数为：两端电源电势相角差为20°，非同步角度为18°，故障类型为AB相间短路。

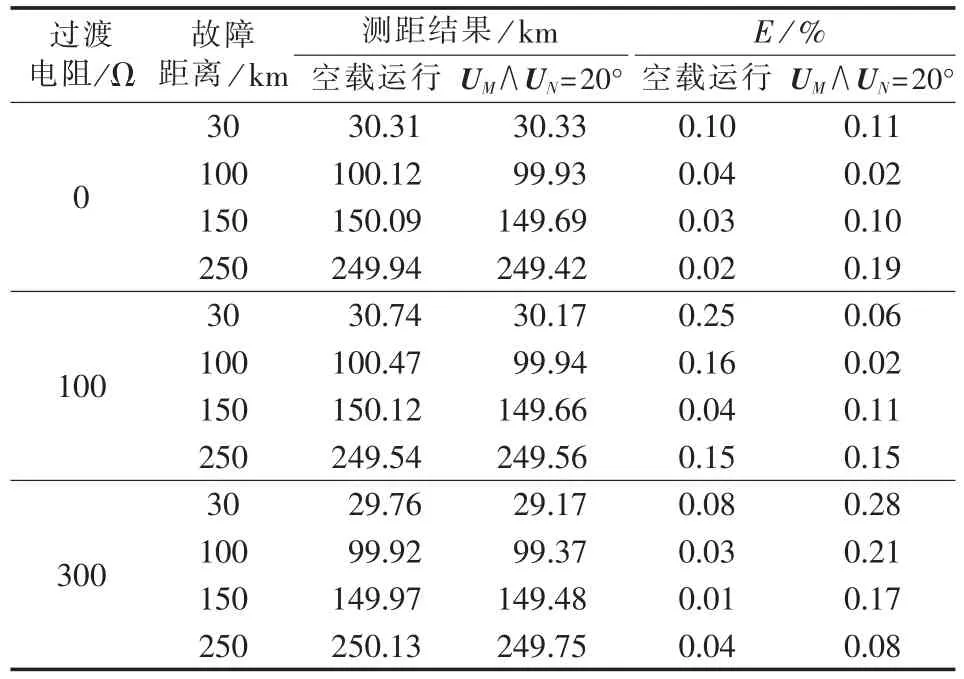
表2 不同故障情况下的测距结果Tab.2 Results of fault location for different fault conditions

由表2结果可知，基于改进参数检测的双端非同步数据故障测距算法，其测距精度不受过渡电阻及负荷电流的影响，测距误差均小于0.5%。

表3所示为在等效线路参数发生变化的情况下，改进参数检测法的测距结果。其他参数为：两端电源相角差为20°，非同步角度为18°，过渡电阻为100 Ω，故障类型为A相接地故障。

表3 线路参数发生变化时的测距结果Tab.3 Results of fault location for different line parameters

由表3可知，当线路参数发生改变时，与补偿前相比，改进参数检测法经过计算补偿后，测距结果仍较为准确，测距误差均小于0.5%。

表4所示为在不同非同步角度时的测距结果和最大误差Emax。其他参数为：两端电源相角差为20°，过渡电阻为100 Ω。

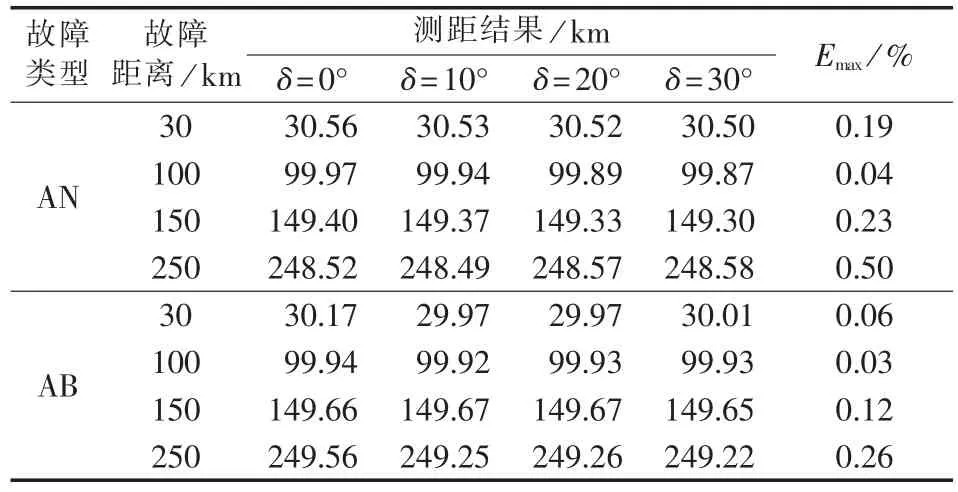
表4 不同非同步角度时的测距结果Tab.4 Results of fault location for different asynchronous angles

由表4结果可知，在经过计算补偿后，基于改进参数检测的双端非同步数据故障测距算法在不同非同步角度条件下仍能得到较为准确的测距结果，最大误差不超过0.5%。

4 基于故障录波数据的算法验证

2013年7月26 日，山东500kV电网益川Ⅰ线（全长80.753 km）发生B相接地故障，实际巡线距离为距益川站68.44 km，录波报告（单端测距）为74.04 km。表5为根据故障前后线路两端录波数据整理的正序电压和电流数据；表6为线路原始参数、根据故障前数据计算出的修正参数、根据本文算法计算出的测距结果等。测距结果表明，本文算法在实际工程应用中具有可信赖的测距精度。

5 线路参数不对称对测距的影响

由于线路绝缘和相关技术方面的原因，500 kV及以上电压等级的单回输电线路多数是水平排列且不换位，这必将导致三相输电线路参数存在一定的不对称。即使对于完全换位线路，线路参数平衡只是从线路始端到末端之间的参数平衡。对于故障测距而言，从故障检测端到故障点，其线路参数极少平衡，只有在完全换位点发生故障时，其线路参数才平衡[16]。

表5 故障前后电压和电流数据Tab.5 Voltage and current data before and after fault

表6 线路参数及测距结果Tab.6 Line parameters and fault location results

表7所示为基于改进参数检测法的双端非同步故障测距算法在线路不同换位情况时的测距结果。

表7 线路不同换位情况时的测距结果Tab.7 Results of fault location for different line transposition conditions

由表7可以看出，线路换位情况对本文算法测距结果影响较小，且这种影响是近似线性的。这是由于在故障点两端换位情况相同的情况下，线路不完全换位或完全不换位对两端线路参数的影响是对称的，经过参数修正补偿后能得到较为理想的结果。

为了更直观地分析线路换位情况对测距的影响，绘制测距结果及误差折线图如图7所示。

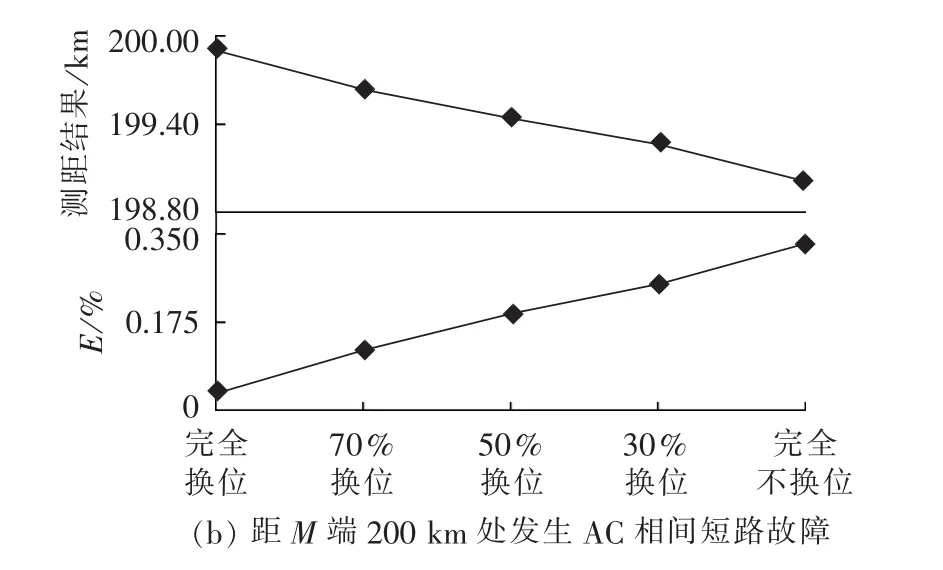
图7 不同换位情况时改进参数检测法测距结果及误差Fig.7 Results of fault location by proposed algorithm and errors for different line transposition conditions

由图7中的测距结果容易看出，线路换位情况对测距结果的影响是近似线性的，而图7所示的测距误差折线与换位情况呈非线性是由于其他因素对测距的影响以及测距误差存在正负性导致的。

6 结论

本文提出了基于改进参数检测法的双端非同步数据故障测距算法。通过实时计算线路参数及非同步角度，克服了线路长度、线路参数的不确定性对测距精度的影响，在线路不完全换位或完全不换位时也能得到较为准确的定位结果。采用正序分量进行计算，无需判断故障类型，具有较好的自适应特性。与拟牛顿法、参数估计法等相比无需迭代，计算量小；与沿线电压趋势法相比，无需满足全线路有且仅有一个点满足电压幅值相等的假设。数字仿真及实际数据验证表明，该测距算法不受系统运行方式、过渡电阻、两端数据不同步等因素的影响，有较高的测距精度和可靠性，适用于利用联网录波数据的故障定位。