利用暂态波形伸缩变换的谐振接地系统故障选线方法
2014-09-28郭谋发郑新桃杨耿杰缪希仁
郭谋发,郑新桃,杨耿杰,高 伟,缪希仁
(福州大学 电气工程与自动化学院,福建 福州 350116)
0 引言
谐振接地系统具有提高系统的供电可靠性、降低雷击损害事故率、抗通信设备电磁干扰等优点,广泛应用于中压配电网。由于谐振接地系统发生单相接地故障的情况复杂多变、故障电流较微弱,且常伴有间歇性电弧,其接地选线问题仍未得到很好解决[1-7]。
利用比故障信号稳态量大若干倍的故障信号暂态量进行选线保护是近年来该领域的研究热点[8-10];所采用的信号量主要有零序电流、零序电压、行波及相电流[11]等;特征量主要有能量、突变量、幅值、极性及波形等;各线路的故障暂态零序电流波形中同时包含了极性、幅值等信息。利用谐振接地系统发生单相接地故障后,非故障线路间的暂态零序电流波形相似,而故障线路与非故障线路暂态零序电流波形差别较大的特点,对暂态零序电流波形或其特征频带做相关分析或灰色关联分析,进而确定接地故障线路,是一个很好的选线思路[12-14]。 文献[15]直接对故障后各线路首个周期的暂态零序电流做两两相关分析;文献[16]将故障后各线路零序电流第1个周期的采样数据减去故障前一个周期对应的采样数据,得到暂态零序电流故障分量,并对其做两两相关分析,利用综合相似度矩阵进行故障选线;文献[17]提出一种改进的灰色关联分析算法,能自动滤除噪声的干扰,增大故障线路零序电流波形和非故障线路零序电流波形间的差异性,提高了选线裕度。
各非故障线路的暂态零序电流大小主要与线路的零序分布电容相关,若采用欧氏距离、曼哈顿距离等方法直接对波形进行相似性分析,暂态零序电流幅值的不同会降低非故障线路零序电流波形间的相似度,基于此提出一种波形伸缩变换方法,采用2条线路对地等效电容的比值对暂态零序电流波形进行伸缩变换,以提高非故障线路的暂态零序电流波形间的相似度及选线裕度。对各线路伸缩变换后的故障暂态零序电流波形作分段线性化处理及分段相平面变换,计算各线路每段故障暂态零序电流波形所有相点到确定点的欧氏距离,形成包含暂态零序电流波形幅值和极性信息的特征矩阵,用模糊K均值聚类(FKM)对特征矩阵进行聚类,选出故障线路。
1 谐振接地系统单相接地故障电流分析
设第k条线路为故障线路,则谐振接地系统发生单相接地时的零序网络等效电路如图1所示。图中,u0为故障点零序电源;R0为零序接地电阻;L0为消弧线圈零序电感;C1、…、Ck-1、Ck+1、…、CN为非故障线路的零序分布电容;Ck为故障线路的零序分布电容;uC为各馈线对地零序分布电容两端的电压;i1、i2、…、iN为各馈线零序电流;iL为流过消弧线圈的电流。
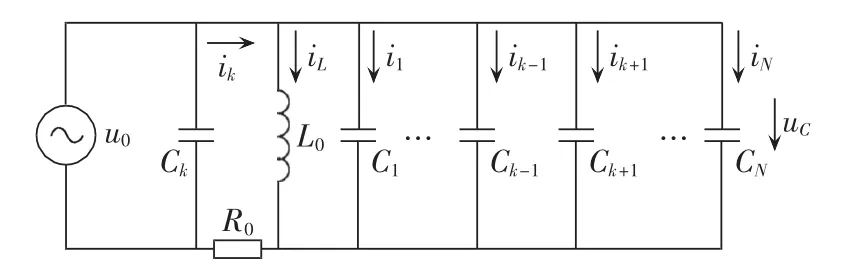
图1 零序网络等效电路Fig.1 Equivalent circuit of zero-sequence network
由图1可知各馈线的零序电流为:

由式(1)可知,非故障线路暂态零序电流ij受同一零序电压uC的作用,变化趋势一致,其区别仅在于对地电容Cj的不同,因此非故障线路间暂态零序电流波形是相似的,其相似程度与各暂态零序电流的幅值及极性有关。由式(2)可知,故障线路暂态零序电流由暂态容性电流和暂态感性电流合成,二者的比例随故障时刻的不同而变化[18]。当接地故障发生在相电压过峰值时,暂态零序电流主要是高频电容电流;当接地故障发生在相电压过零点时,暂态零序电流主要是低频感性电流;故障线路与非故障线路暂态零序电流相互间波形差异较大。
2 波形伸缩变换法选线原理
2.1 暂态零序电流波形的伸缩变换
由式(1)可得:

由式(3)可知,若把第j条线路的故障暂态零序电流除以其对地等效电容Cj,则非故障线路间暂态零序电流波形的相似性将提高。各线路对地等效电容Cj难以获取,引入伸缩变换系数对暂态零序电流波形进行变换。以第b条线路作为参考线路,定义第j条线路的伸缩变换倍数pj为:
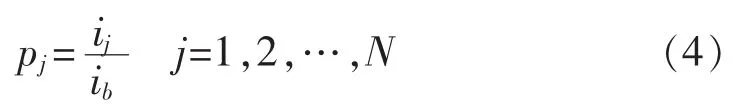
其中,ij、ib为线路j和线路b的故障暂态零序电流。考虑到暂态零序电流波形具有非线性非平稳特征,采用稳态时的ij和ib求pj。为减少噪声等因素的影响,用故障后第q个1/4周期采样数据的平均倍数求pj,暂态过程可能持续1~2个周期,q的取值应大于8。假设采样频率为20 kHz,则用故障后零序电流的第100(q-1)+1个采样点到第100q个采样点的平均伸缩变换倍数求pj,如式(5)所示。

下面考虑第b条线路即参考线路为故障线路及非故障线路2种情况,分析伸缩变换处理对各线路暂态零序电流波形的影响。
a.参考线路为非故障线路(b≠k)。
由式(3)和式(4)可得:

结合式(1)、式(4)和式(6)可得非故障线路暂态零序电流经伸缩变换后的表达式为:
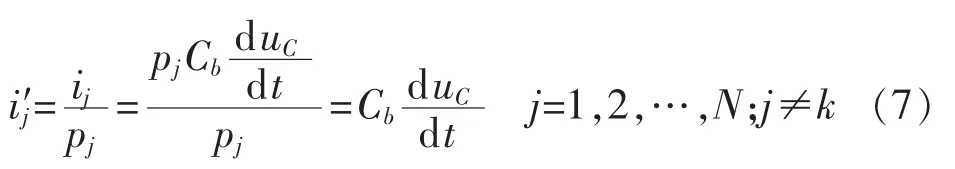
结合式(2)和式(4)可得,故障线路暂态零序电流经伸缩变换后的表达式为:

在参考线路为非故障线路的情况下,由式(7)可知,经伸缩变换处理后,各非故障线路暂态零序电流具有相同的表达式,伸缩变换处理提高了非故障线路间暂态零序电流波形的相似性。比较式(7)和式(8)可知,经伸缩变换处理后,故障线路和非故障线路暂态零序电流波形间的差异仍较大。
b.参考线路为故障线路(b=k)。
由式(6)知,各非故障线路等效对地电容可用某非故障线路(编号a,a≠b)等效对地电容Ca表示:
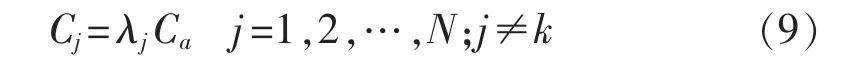
其中,λj为比例系数。
据式(1)、式(9)可得:
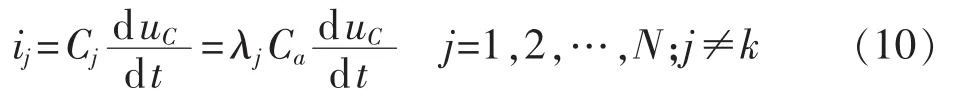
令 pa=ia/ib,则由式(2)、式(10)可得:
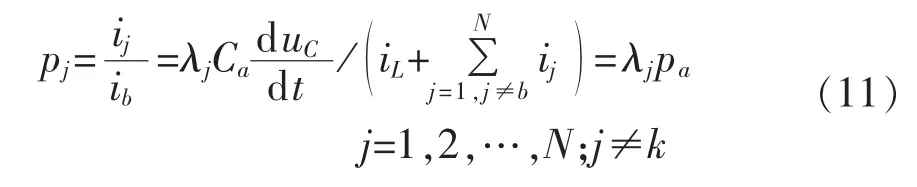
由式(10)、式(11)可知:
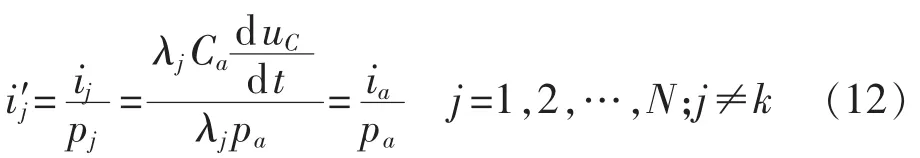
参考线路为故障线路时,故障线路暂态零序电流波形保持不变。由式(12)可知,经伸缩变换处理后,各非故障线路的暂态零序电流表达式相同,具有较强的相似性,伸缩变换处理提高了非故障线路暂态零序电流波形间的相似性;比较式(2)和式(12)可知,经伸缩变换处理后,故障线路和非故障线路暂态零序电流波形的差异仍较大。
2.2 基于相平面分析的特征矩阵构造方法
相平面分析是时域波形特征提取的有效方法,在电弧故障检测、电能质量扰动分类及接地故障类型分类[19]等领域得到应用。相平面是以时间序列x(t)为横轴,时间序列的导数 x˙(t)为纵轴所构成的平面,它以另一种形态表征原始波形。如图2所示,以正弦函数 y=Assinx(As为幅值,xє[0,2π])为例,当As=1、x从0增大到π时,其相平面轨迹如曲线1所示,相轨迹从点A沿实线到点B,分布在第Ⅰ、Ⅳ象限;当As=1、x从π增大到2π时,其相平面轨迹如曲线2所示,相轨迹从点B沿虚线到点A,分布在第Ⅱ、Ⅲ象限;当As=1.5、x从0增大到π时,其相平面轨迹如曲线3所示,相轨迹从点C沿实线到点D,分布在第Ⅰ、Ⅳ象限。由此可知,对于一个周期内某一段特定的正弦波,其相平面轨迹是唯一的,且正弦波的幅值越大,其相轨迹偏离原点的距离也越大。

图2 正弦波相平面轨迹示意图Fig.2 Schematic diagram of sine wave trajectory on phase-plane
i′j(n)为伸缩变换后第 j条线路的暂态零序电流波形的离散时间序列,n为采样点号,其对应点的导数可由式(13)求取。
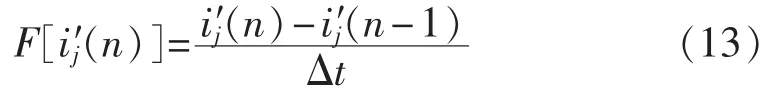
其中,F[i′j(n)]为 i′j(n)的导数;Δt为采样步长。
由式(13)可知,F[i′j(n)]只与当前采样值 i′j(n)和上一次采样值 i′j(n-1)有关,而与其他采样值无关,易受到随机干扰和噪声的影响。将变换后的暂态零序电流在时域上等分为N1段,采用最小二乘估计法拟合[20]对各段进行线性化处理,得到N1个直线段,那么零序电流波形在某直线段范围内的点的导数 F[i′j(n)]均用该直线段的斜率来表示。
因故障暂态零序电流第1个半周波(首半波)的暂态过程明显,包含了极性、幅值等信息,可求取其时域特征矩阵用于选线。设暂态零序电流首半波的采样点数为Ks,将各线路变换后的暂态零序电流i′j平均分成 N2(N1=gN2,g≥2,g 为整数)段,则每个分段上采样点的个数为Ks/N2。逐段作相平面变换,并对每一段相平面图上的点按式(14)进行归一化处理,使相平面上的数据点都落在区间[-1,1]。

其中,i′jm(n) 表示 i′j的第 m 个分段(m=1,2,…,N2;n=1,2,…,Ks/N2);表示各分段中的最大值。
为综合利用故障暂态零序电流的幅值和极性信息进行接地选线,计算每一段伸缩变换后的暂态零序电流波形的相轨迹到相平面确定点(-1,0)的欧氏距离,如式(15)所示。
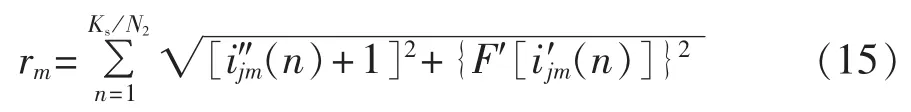
其中,rm为第m段相平面轨迹到确定点(-1,0)的欧氏距离。
由图2可知,正弦波在相平面上的轨迹为椭圆,具有轴对称关系。计算曲线1和曲线2到原点的欧氏距离,会得到相同的距离值,无法区分正弦波的正负半周;但计算曲线1和曲线2到确定点(-1,0)的欧氏距离,则可以分辨曲线1和曲线2的差异。如果直接计算曲线 y=sin x(xє[0,2π])以及 y=-sin x(x є[0,2π])的相轨迹到确定点(-1,0)的欧氏距离,也会得到相同的距离值,不能正确区别2条曲线;将曲线分成多段,分别计算每段相点到确定点(-1,0)的欧氏距离,则由算得的多个欧氏距离值可分辨两曲线的差异。考虑到单相接地时,故障线路与非故障线路暂态零序电流波形间的相轨迹关系与曲线1和曲线2间的相轨迹关系相类似,因此采用分段相平面变换,计算每一段波形的相轨迹到确定点(-1,0)的欧氏距离,用于判别故障线路和非故障线路的暂态零序电流波形。
将rm作为暂态零序电流某一时间段波形的局部特征量,则任意一条线路的暂态零序电流波形的全局特征量可表示为:

则N条线路的全局特征量构成一个N×N2的特征矩阵 S,如式(17)所示。
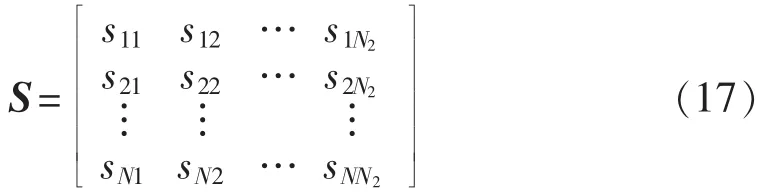
其中,sji表示第j条线路的第i段相轨迹到确定点(-1,0)的欧氏距离。
为增强可比性,对特征矩阵S中的元素按列做归一化处理,得到:

2.3 模糊K均值聚类选线
模糊K均值聚类是一种基于模糊划分的聚类方法。该算法需要输入待分类的H个向量xj(j=1,2,…,H)的K组分类的初始模糊隶属度矩阵U(1):
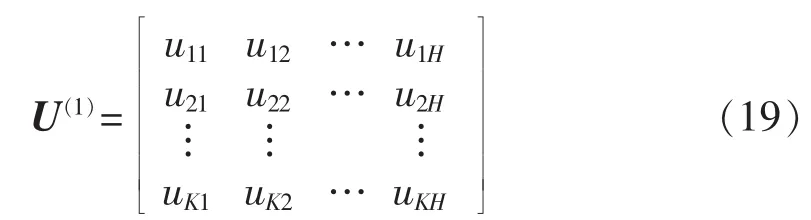
其中,uij表示第j个向量属于第i类的隶属度,uijє[0,1]且。设 vi为第 i类初始聚类中心向量,则初始聚类中心矩阵为:

确定目标函数 JM(U,V),有:
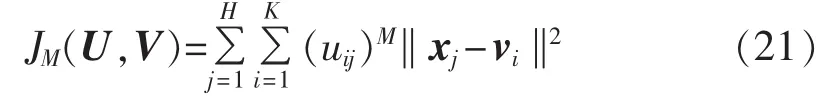
其中,M的值与最终分类的模糊程度有关,为使JM的最终分类达到局部最优,取M=2,利用拉格朗日乘数法证明可得:
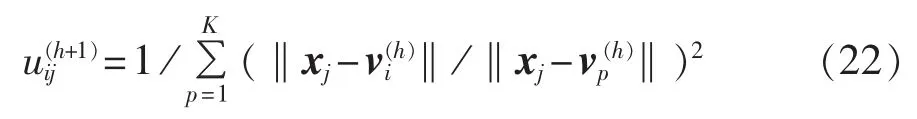
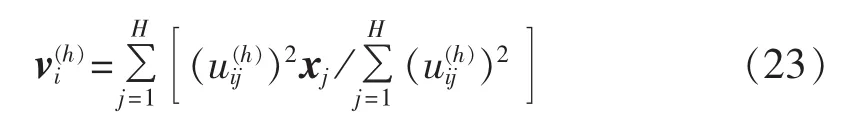
其中,h为迭代次数计数器。
模糊K均值聚类通过以下步骤来确定聚类中心矩阵V和隶属度矩阵U:
a.确定分类数K,令h=0,随机给出初始隶属度矩阵 U(1);
b.据式(23)计算初始分类的聚类中心向量 V(1);
c.据式(22)计算隶属度矩阵 U(h+1);
d.给定收敛条件Δ(本文取0.0001),如果2次迭代计算所得的隶属度矩阵差值小于Δ,则迭代结束,否则返回步骤b继续迭代,直至达到收敛条件或到达预定迭代次数为止。
在接地选线工程应用中,利用模糊K均值聚类将各线路故障暂态零序电流波形的特征矩阵S分成2类,可得隶属度矩阵:

其中,uij为第 j条线路属于第 i(i=1,2)类的隶属度。由隶属度矩阵U可确定隶属于第1类的线路和隶属于第2类的线路,被单独分为一类的线路即为故障线路。
2.4 接地选线流程
接地选线流程如图3所示。以零序电压是否越限作为启动接地选线的依据,若发生单相接地,则对故障暂态零序电流的首半波做伸缩变换;对变换后的波形按时间等分,求各段波形的相平面轨迹,计算每一段波形对应的相点到确定点(-1,0)的欧氏距离,形成特征矩阵S并对其按列做归一化处理;采用模糊K均值聚类将特征矩阵S分为2类,由于非故障线路的暂态零序电流波形较为相似而被归为一类,故障线路暂态零序电流波形则被单独归为另一类,实现选线。
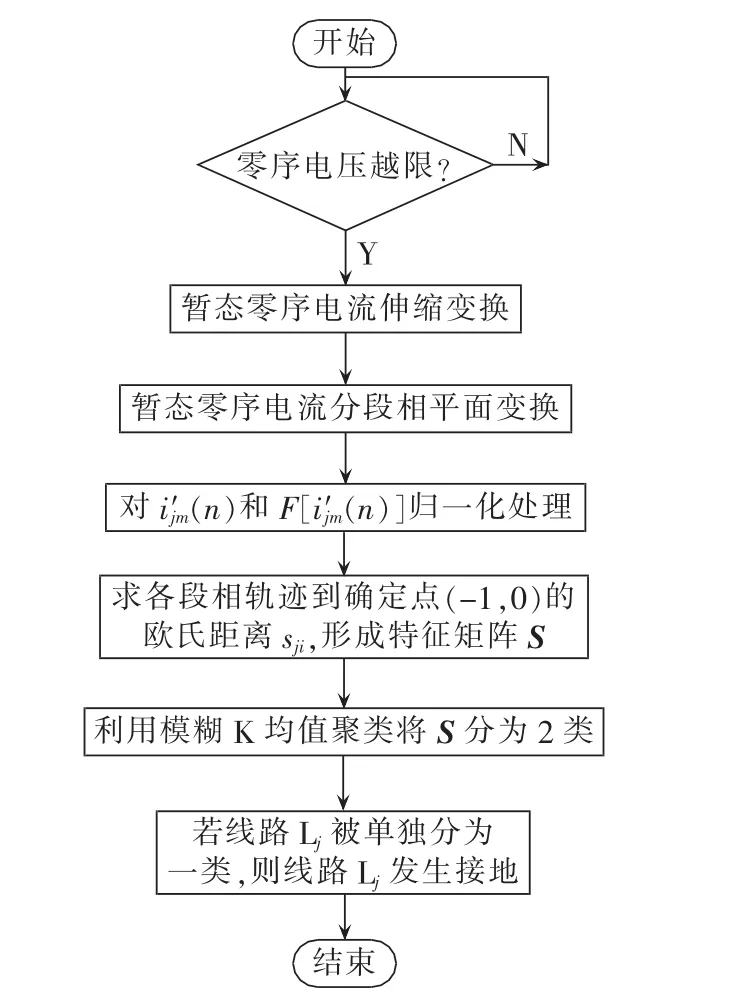
图3 接地选线流程图Fig.3 Flowchart of faulty line detection
3 选线方法的仿真验证
利用ATP搭建一个含6条出线的谐振接地系统模型,见图4。图中,Rf为接地电阻;架空线路的正序参数为ro1=0.17 Ω/km,lo1=1.21 mH/km,co1=0.009 7 μF/km;架空线路的零序参数为 ro0=0.23 Ω/km,lo0=5.478 mH/km,co0=0.008 μF/km;电缆线路的正序参数为 rc1=0.27 Ω/km,lc1=0.255mH/km,cc1=0.339μF/km;电缆线路的零序参数为rc0=2.7 Ω/km,lc0=1.019mH/km,cc0=0.28 μF/km。 系统总电容电流IC=3ωC∑UN=36A>20A(ω为基波角频率;UN为额定相电压;C∑为系统中所有线路的单相对地电容之和),应装设消弧线圈。取消弧线圈的过补偿度为 5%,则电感 L=1/1.05×UN/(ωIC)=0.49 H;消弧线圈的有功损耗大约为感性损耗的2.5%~5%,取 3%,则电阻 RL=0.03 ωL=4.58(Ω)。
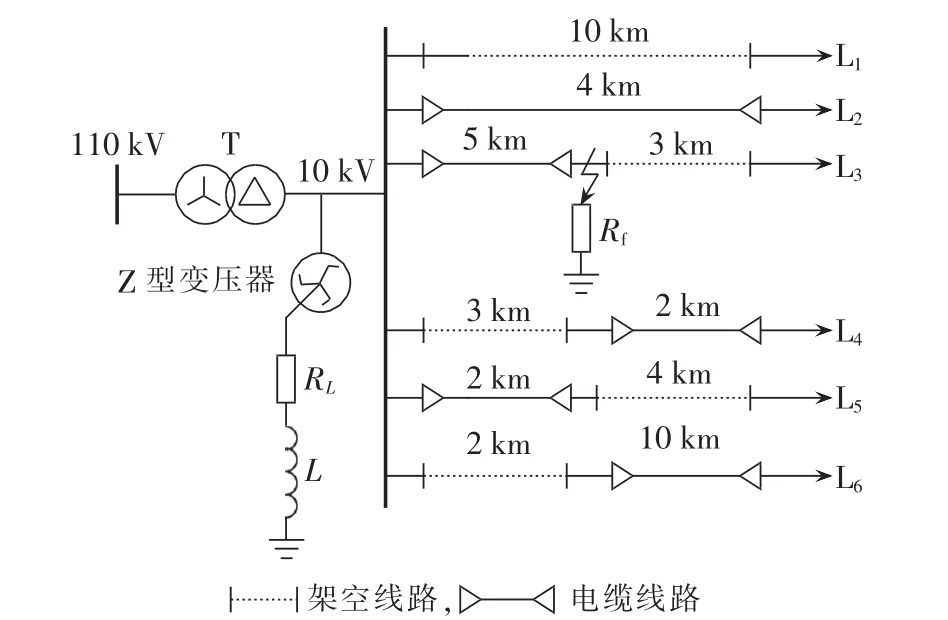
图4 谐振接地系统仿真模型Fig.4 Simulation model of resonance-grounding system
以L3距离母线5 km处发生故障合闸角为60°、接地电阻为100 Ω的单相接地故障为例,说明选线过程。采样频率为20 kHz,故障线路和其中2条非故障线路的暂态零序电流首半波波形如图5(a)所示。选取L4作为参考线路,各线路暂态零序电流按变换系数 pk=ik/i4做伸缩变换,变换后波形如图 5(b)所示。由图5可知,经伸缩变换后,非故障线路暂态零序电流波形间的相似度得到提高,故障线路与非故障线路波形间的相似度变化较小。
将伸缩变换所得的故障暂态零序电流首半波分为N1=20段,做分段线性化,用各直线段的斜率表示暂态零序电流波形在该直线段范围内的点的导数,得其相平面轨迹;取N2=10,将相平面轨迹分为10段并对各段做归一化处理。求取各线路每段暂态零序电流的相轨迹点到确定点(-1,0)的欧氏距离,形成特征矩阵S,对S按列归一化处理可得:


图5 故障暂态零序电流波形Fig.5 Fault zero-sequence transient current waveforms
对S进行模糊K均值聚类,得隶属度矩阵U:

隶属度矩阵U的行对应故障状态,第1—6列分别对应第1—6条线路,U中每一列值最大的元素所在的行即为该线路对应的状态(如下划线所示)。由隶属度矩阵U可知,L3属于一类,其他线路属于另一类,L3被单独归为一类,由此可判定L3为接地线路。
若不对各线路故障暂态零序电流波形做伸缩变换,其他步骤不变,则特征矩阵S′和隶属度矩阵U′分别为:
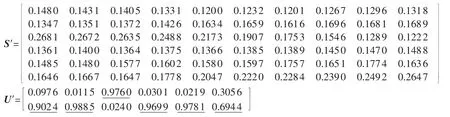
由隶属度矩阵U′也可正确判定L3接地,但通过比较二者的特征矩阵和隶属度矩阵可以知道,对暂态零序电流波形进行伸缩变换能够提高选线裕度。
不同线路在不同接地电阻、不同故障点和不同故障合闸角情况下发生单相接地故障的选线结果见表1。表中,Xf为故障点到母线的距离;Rf为接地电阻;θ为故障合闸角。
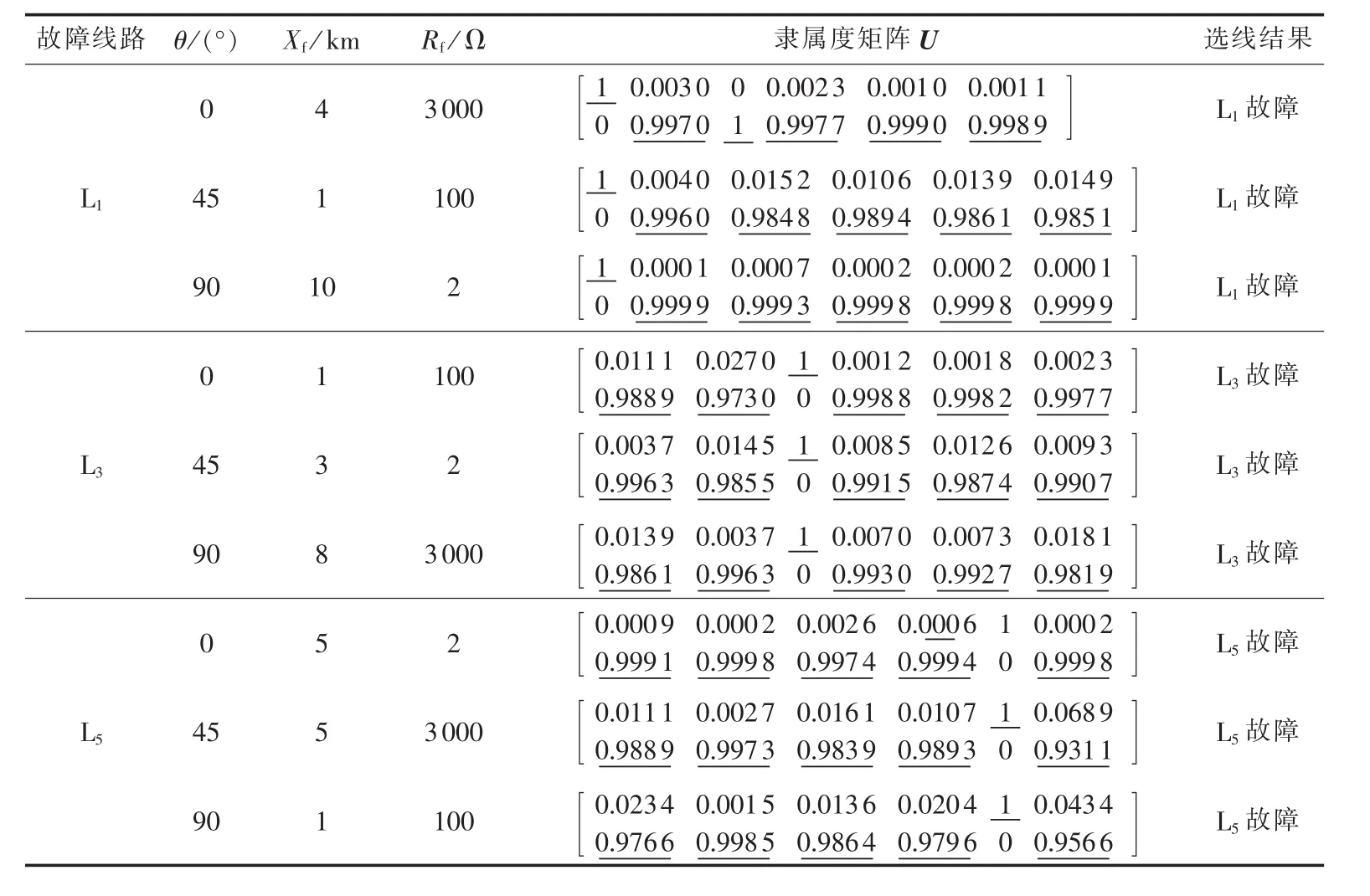
表1 故障选线结果Tab.1 Results of faulty line detection
4 选线方法的适应性
4.1 电弧故障
单相接地初期多表现为间歇性电弧故障,采用mayr电弧模型进行电弧故障仿真。线路L3在距母线5 km处发生电弧接地故障的选线结果见表2。
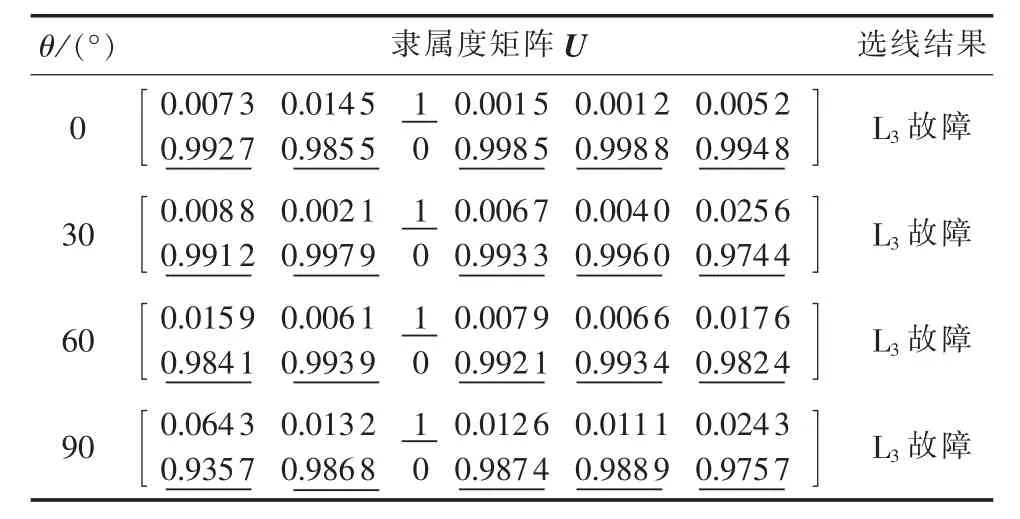
表2 线路L3发生电弧故障时的选线结果Tab.2 Results of faulty line detection for arc fault of L3
4.2 不同时间窗
线路L4在距离母线2 km处发生故障合闸角为90°、接地电阻为3 kΩ的单相接地故障,选用不同的暂态零序电流时间窗,选线结果见表3。
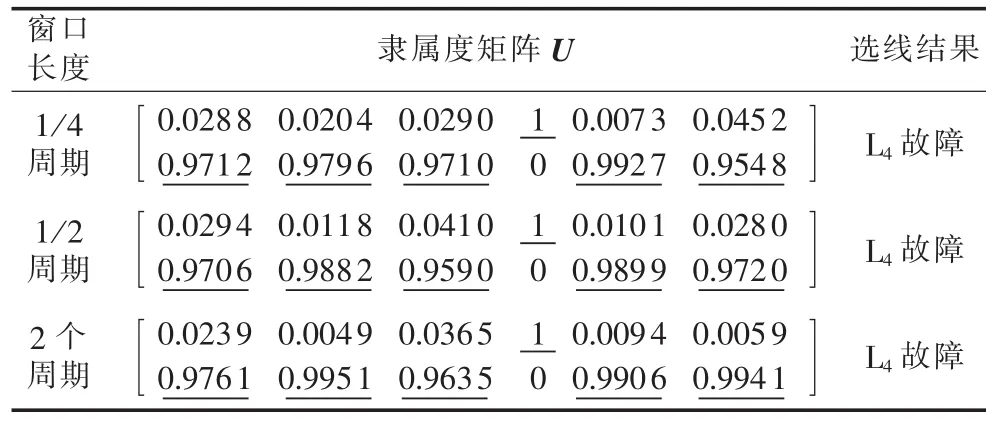
表3 线路L4在不同时间窗下故障选线结果Tab.3 Results of faulty line detection with differenttime window sizes for L4
4.3 叠加噪声
工程应用中,需考虑外界随机噪声干扰对选线方法的影响。叠加信噪比为20 dB的高斯白噪声干扰,线路L6在3种典型接地故障情况下的选线结果见表4。由表4可见,该选线算法具有较强的抗干扰能力。
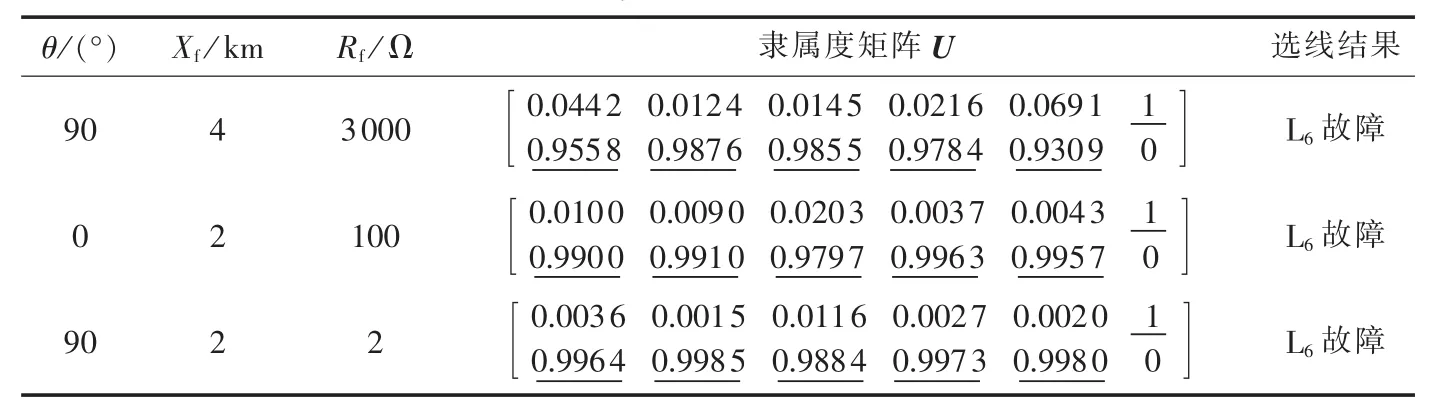
表4 线路L6在叠加噪声情况下的选线结果Tab.4 Results of faulty line detection with noises for L6
4.4 采样不同步
接地故障发生后选线装置对各线路零序电流的采样可能存在不同步。考虑线路L3、L4滞后线路L1、L28个采样点;线路 L5、L6滞后线路 L1、L214个采样点,线路L3末端发生接地电阻为3 kΩ的单相接地故障,其选线结果见表5。
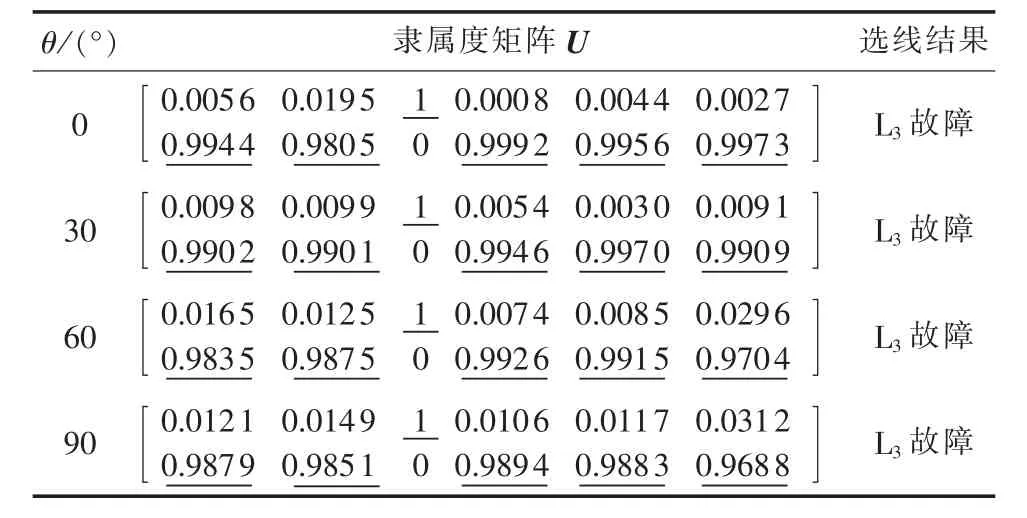
表5 采样不同步情况下的选线结果Tab.5 Results of faulty line detection with asynchronous sampling
5 结论
对伸缩变换后的故障暂态零序电流波形进行分段相平面分析,进而构造各线路暂态零序电流波形的特征矩阵,对特征矩阵做模糊K均值聚类,选出故障线路。得到的主要结论如下。
a.波形伸缩变换可提高非故障线路暂态零序电流波形间的相似度及选线裕度。基于分段相平面分析所构造的特征矩阵可综合表征暂态零序电流波形的幅值和极性信息。
b.对特征矩阵做模糊K均值聚类,可在不设置阈值的情况下选出故障线路。但对于母线故障,需增加检测其进线的故障暂态零序电流。
c.所提选线方法适用于噪声干扰、电弧故障、采样不同步、不同时间窗等工程应用中可能存在的影响因素。
