半环诱导赋值代数的轮廓解
2014-09-06许格妮李永明
许格妮, 李永明, 张 云
(1.陕西师范大学 数学与信息科学学院, 西安 710062; 2.西安财经学院 统计学院, 西安 710100)
半环诱导赋值代数的轮廓解
许格妮1,2, 李永明1, 张 云2
(1.陕西师范大学 数学与信息科学学院, 西安 710062; 2.西安财经学院 统计学院, 西安 710100)
先对全序半环诱导的赋值代数的轮廓解性质进行研究, 再在全序半环诱导的赋值代数中引入保轮廓解的概念, 并借助轮廓解的性质, 对转移函数f保全序半环诱导的赋值代数的轮廓解问题进行研究.结果表明, 若转移函数f是一个半环同态, 则f是保轮廓解的.
赋值代数; 半环; 轮廓解; 转移函数
0 引 言
赋值代数是从人工智能领域中包括约束系统、信任函数系统、数据库理论等抽象出来的用于描述信息处理方式的一种特殊代数结构模型, Kohlas[1]对其进行了明确、完整的表达.在一个赋值代数系统中, 系统通过对变量的赋值表达知识和信息, 并通过联合运算对信息进行合成, 通过投影运算得到在指定变量集上的相关信息, 从而完成信息的提取.赋值代数是非确定情形下知识表示和推理的重要工具.
局部计算是赋值代数的一个核心内容, 目前已有很多研究结果[2-6].在半环所诱导的赋值代数中, 投影运算可转化为求和运算.特别地, 在全序半环诱导的赋值代数中, 求和运算即为求最大值运算.因此, 对于全序半环赋值φ∈Φ, 当投影到空集时, 满足等式φ(x)=φ↓Ø(◇)的x即为使得φ取最大值的轮廓,φ↓Ø(◇)即为该赋值的最大值.基于此, 文献[3]在全序半环所诱导的赋值代数中提出了轮廓解的概念, 并给出了寻求轮廓解的一种算法; 文献[7-8]对轮廓解的性质进行了初步探讨.本文在此基础上对轮廓解的一些性质及其与扩展解之间的关系进行进一步研究, 并对轮廓解的求法提出一种新思想: 当直接寻求一个赋值的轮廓解存在困难时, 可以将其转移到新系统的一个赋值上, 通过求解新赋值的轮廓解获得原问题的信息, 从而给出了在全序半环诱导的赋值代数中转移函数保轮廓解的判别方法.
1 预备知识
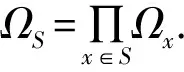
一般可通过对变量赋值传达知识或信息, 本文将该赋值用φ,ψ…表示, 用Φ,Ψ…表示由这些赋值构成的集合.
定义1[1]设(Φ,D)是一个具有如下3种运算的二元组, 其中(D,∨,∧)是一个格:
1) 论域运算:Φ→D;φ→d(φ);
2) 联合运算:Φ×Φ→Φ; (φ,ψ)→φ⊗ψ;
3) 投影运算:Φ×D→Φ; (φ,T)→φ↓T.
若系统(Φ,D)满足如下公理, 则称其为一个带标记的赋值代数:
1) 半群律:Φ关于联合运算满足交换律与结合律, 且有单位元;
2) 论域律: 若∀φ,ψ∈Φ, 则有d(φ⊗ψ)=d(φ)∨d(ψ);
3) 边缘化律: ∀φ∈Φ,T∈D, 若T≤d(φ), 则有d(φ↓T)=T;
4) 传递律: 若∀φ∈Φ,T≤S≤d(φ), 则(φ↓S)↓T=φ↓T;
5) 联合律: ∀φ,ψ∈Φ, 若d(φ)=S,d(ψ)=T, 则有(φ⊗ψ)↓S=φ⊗ψ↓S∧T;
6) 单位元律: ∀S,T∈D, 有eS⊗eT=eS∨T.
例1设A是一组属性集, 对任意一个属性α∈A, 用非空集Uα表示α可能的取值.设x∈A, 若∀α∈x, 有f(α)∈Uα, 则称定义域为x的函数f是一个x元组.符号Ex表示所有x元组构成的集合.若R⊆Ex, 则称R为x上的一个关系,x称为这个关系的域, 记d(R)=x.
1) 对于x,y上的两个关系R,S, 它们的联合定义域是x∪y上的关系, 满足:
R▷◁S={f:f∈Ex∪y,f[x]∈R,f[y]∈S},
其中f[x]表示x元组f在x上的投影.
2) 对于x上的一个关系R, 若y⊆x, 则定义关系R在y上的投影为πy(R)={f[y]:f∈R}.
给定一个属性集A, 记R为由该属性集子集上所有关系构成的集合, 则由文献[1]知, 系统(R,A)在上述定义的标记运算、联合运算及投影运算下构成一个赋值代数.
定义2[2]设非空集合L上有两个二元运算+,×, 且元素0,1∈L, 若下列条件成立, 则称(L,+,×,0,1)是一个半环:
1) 加法和乘法均满足交换律和结合律;
2) 乘法在加法上满足分配律;
3) ∀a∈L, 有a+0=a,a×0=0, 0称为L的零元;
4) ∀a∈L, 有a×1=a, 1称为单位元.
在半环L上定义关系:a≤b⟺a+b=b, 由文献[2]知, 若在L上定义的该序关系是全序, 则∀a,a′,b,b′∈L, 有:
1)a+b=max{a,b};
2) 若a≤b,a′≤b′, 则a+a′≤b+b′,a×a′≤b×b′.
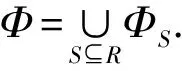
令D=P(r), 在(Φ,D)上定义如下运算:
1) 联合运算: ∀φ∈ΦS,ψ∈ΦT及x∈ΩS∪T, 定义φ⊗ψ(x)=φ(x↓S)ψ(x↓T);
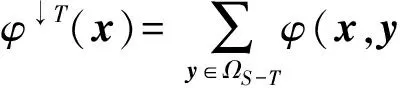
文献[2]已证明: 该系统在上述运算下构成一个赋值代数, 称其为由半环L诱导的赋值代数.
2 半环诱导赋值代数轮廓解的性质
在全序半环所诱导的赋值代数中,φ↓Ø(◇)=max{φ(x):x∈Ωd(φ)}, 则满足φ(x)=φ↓Ø(◇)的x即为φ取最大值的轮廓, 而对应的φ(x)即为φ的最大值.为考察一个赋值φ对应的这样解的情况, 文献[3]在全序半环所诱导的赋值代数中引入了轮廓解与扩展解的概念, 并对其性质进行了研究.本文在这些工作的基础上对全序半环所诱导赋值代数轮廓解的性质及其与扩展解的关系进行进一步研究.
定义3[3]设(Φ,D)是由全序半环所诱导的赋值代数, 对于φ∈ΦS, 如果x∈ΩS满足φ↓Ø(◇)=φ(x), 则称x为φ的一个轮廓解,φ的全体轮廓解之集记为Cφ.
例2设L=({0,1,a,b},∨,∧,0,1)是四元链格, 其中0 φ:ΩS→L, (0,0)→1, (0,1)→1, (1,0)→a, (1,1)→b, 则Cφ={(0,0),(0,1)}. 注1特别地, 若S∩T=Ø时, 则有(x1,x2)∈Cφ⊗ψ. 定理1的逆命题未必成立, 如: 推论1设(Φ,D)是由全序半环所诱导的赋值代数, 取φ∈Φ且φ=φ1⊗φ2⊗…⊗φn, 其中d(φi)=Si,i=1,2,…,n, 且当i≠j时,Si∩Sj=Ø.如果xi∈Cφi, 则(x1,x2,…,xn)∈Cφ. 注2上述结论表明: 若φ=φ1⊗φ2⊗…⊗φn, 通过寻求赋值φi的轮廓解并不能完全得到φ的轮廓解, 但提供了寻求赋值轮廓解的一种方法. 即c∈Cφ↓S-T. 定理2的逆命题未必成立, 如: 定理3[4]设(Φ,D)是由全序半环所诱导的赋值代数, 若d(φ)=S,d(ψ)=T, 且S∩T⊆U⊆S∪T, 则有(φ⊗ψ)↓U=φ↓S∩U⊗ψ↓T∩U. φ(x↓U∩S,c1)×ψ(x↓U∩T,c2)=φ↓U∩S(x↓U∩S)×ψ↓U∩T(x↓U∩S), 因此有 定义5设f:L→L′是两个全序半环间的一个映射, (Φ,D)与(Ψ,D)分别为半环L,L′诱导所得的赋值代数, 对于Φ中的任一赋值φ:Ωs→L, 有复合映射fφ:Ωs→L′, 显然fφ∈Ψ.因此, 称映射f为Φ的转移映射. 定义6设f:L→L′是两个全序半环间的一个映射, (Φ,D)是由半环L诱导的赋值代数, 如果f满足∀φ∈Φ, 有Cφ⊆Cfφ, 则称f是保轮廓解的. 定义7[5]设f是两个半环(L,+,×,0,1)与(L′,+,×,0,1)间的一个映射, 若f满足: 1)f(0)=0,f(1)=1; 2)f(a+b)=f(a)+f(b); 3)f(a×b)=f(a)×f(b). 则称f是一个半环同态. 引理1设(Φ,D)是由全序半环L所诱导的赋值代数,f是两个全序半环L,L′间的一个映射, 即f:L→L′, 且有f(0)=0,f(1)=1, 若对任意的正整数m,n, 有 则f是一个半环同态, 其中∀uij,vij∈L,i=1,2,…,n;j=1,2,…,m. 证明: 若式(1)成立, 则f是单调的.事实上, 在式(1)中, 令m=n=1即可得. 下证∀a,b∈L, 有f(a)+f(b)=f(a+b).由f单调可得,f(a)+f(b)≤f(a+b).假设f(a)+f(b) 再证f(ab)=f(a)(b).假设f(ab)≠f(a)f(b), 则有f(a)f(b) 综上可知,f是一个半环同态. 定理5设(Φ,D)是由全序半环L所诱导的赋值代数,f是两个全序半环L,L′间的一个映射, 且有f(0)=0,f(1)=1, 若式(1)成立, 则f是保轮廓解的. 由引理1知,f是一个半环同态, 因此有 因此有 定理5给出了转移函数f保轮廓解的一个判别条件, 但有时验证式(1)是否成立较麻烦, 下面给出定理5的另一种表示形式. 引理2设(Φ,D)是由全序半环L所诱导的赋值代数,f是两个全序半环S,S′间的一个映射, 即f:L→L′, 且有f(0)=0,f(1)=1, 则f是一个半环同态当且仅当式(1)成立. 证明: 由引理1知, 仅证必要性即可.若f是一个半环同态, 则f是单调的.事实上, ∀a,b∈S, 若a≤b, 则有f(a)+f(b)=f(a+b)=f(b), 因此f(a)≤f(b). 由f是一个半环同态可得 因此, 式(1)成立. 综上, 可得: 定理6设(Φ,D)是由全序半环L所诱导的赋值代数,f是两个全序半环L,L′间的一个映射, 且有f(0)=0,f(1)=1, 若f是一个半环同态, 则f保轮廓解. 当直接寻求某个赋值φ的轮廓解存在困难时, 可借助定理6, 通过一个半环同态映射f将其转移到一个结构较简单的、新的赋值代数系统中, 通过给出fφ的轮廓解解决原问题. 例5近期某类动物有一种疾病, 医务专家对此不能确诊, 但凭借多年医学经验一致认为服用三唑核苷、氧氟沙星、阿奇霉素或胸腺素这4种药有助于该疾病的好转.多名医务专家对该类动物按不同组合服用这几种药物给出评价, 结果列于表1, 其中:x1,x2,x3,x4依次表示上述4种药物, 若服用药物xi, 则取xi=1, 否则取xi=0(i=1,2,3,4);φ表示是否服用各药物与医务专家给出分值之间的对应关系.求最佳服用方案. 表1 药物服用情况分值结果Table 1 Score results about taking medicine 上述问题求最佳方案实际上是找φ的轮廓解, 为了找出φ的轮廓解, 需要在所有φ(x1,x2,x3,x4)中搜索出使φ取最大值的轮廓.当φ取值较多时, 用逐一搜索法找出其轮廓解显然较麻烦, 但借助定理6可缩小搜索范围, 从而减少了运算量. 假设L1={[0,100],∨,∧,0,100}, 则上述φ可视为由全序半环L1所诱导的赋值代数(Φ,D)中的一个赋值, 其中Φ={f:ΩT→L1},T={x1,x2,x3,x4},D=P({x1,x2,x3,x4})是{x1,x2,x3,x4}的幂集.令L2={{0,a,b,1},∨,∧,0,1}, 其中0 表2 复合映射fφTable 2 Composite mapping fφ 由表2知Cα·φ={(0110),(1100),(0111)}, 则由定理6, 只需在Cα·φ中搜寻φ的轮廓解即可:φ(0110)=90,φ(1100)=90,φ(0111)=95, 因此Cφ={0111}, 即服用氧氟沙星、阿奇霉素和胸腺素为最佳方案. [1]Kohlas J.Information Algebras: Generic Structures for Inference [M].London: Springer-Verlag, 2003. [2]Kohlas J, Wilson N.Semiring Induced Valuation Algebras: Exact and Approximate Local Computation Algorithms [J].Artif Intell, 2008, 172(11): 1360-1399. [3]Pouly M.A Generic Framework for Local Computation [D].Fribourg, Switzerland: University of Fribourg, 2008. [4]韩邦合.赋值代数分裂算法与隐性半环赋值研究 [D].西安: 陕西师范大学, 2011.(HAN Banghe.The Splitting Algorithm of Valuation Algebra and Implicit Valuation over a Semiring [D].Xi’an: Shaanxi Normal University, 2011.) [5]LI Sanjiang, YING Mingsheng.Soft Constraint Abstraction Based on Semiring Homomorphism [J].Theoretical Computer Science, 2008, 403(2/3): 192-201. [6]GUAN Xuechong, LI Yongming.On a Condition for Semirings to Induce Compact Information Algebras [J].Electronic Notes in Theoretical Computer Science, 2014, 301: 39-48. [7]Kohlas J.Lecture Notes on the Algebraic Theory of Information [R/OL].2010-11-24.http://diuf.unifr.ch/drupal/tns/sites/diuf.unifr.ch.drupal.tns/files/file/kohlas/main.pdf. [8]管雪冲.赋值代数中若干问题的研究 [D].西安: 陕西师范大学, 2011.(GUAN Xuechong.The Study of Some Questions about Valuation Algebra [D].Xi’an: Shaanxi Normal University, 2011.) SolutionConfigurationofSemiringValuationAlgebra XU Geni1,2, LI Yongming1, ZHANG Yun2 The properties of the solution configuration of valuation algebra over a totally ordered semiring were discussed.Furthermore, the concept of preserving the solution configuration of valuation algebra over a totally ordered semiring was given.With the help of the properties of the solution configuration, the question of the transfer functionfpreserving solution configuration was studied.It is concluded that the transfer functionfpreserves solution configuration iffis a semiring homomorphism. valuation algebra; semiring; solution configuration; transfer function 2014-03-12. 许格妮(1978—), 女, 汉族, 博士研究生, 讲师, 从事计算智能、信息代数与不确定推理的研究, E-mail: geniwork@163.com.通信作者: 李永明(1966—), 男, 汉族, 博士, 教授, 博士生导师, 从事计算智能、量子逻辑和量子计算的研究, E-mail: liyongm@snnu.edu.cn. 国家自然科学基金(批准号: 11271237; 61228305)和西安财经学院科研基金(批准号: 12JD04). O141 A 1671-5489(2014)06-1119-06 10.13413/j.cnki.jdxblxb.2014.06.03 赵立芹)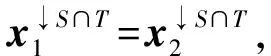
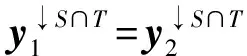
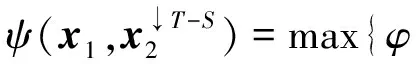
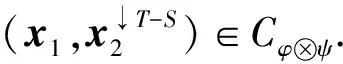
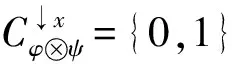
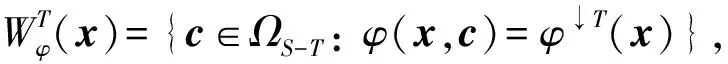

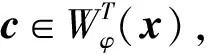
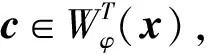
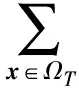
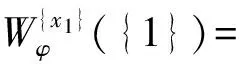
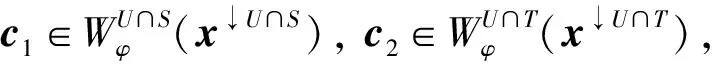
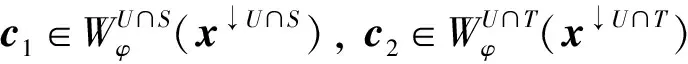
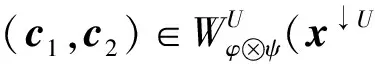
3 半环诱导赋值代数的保轮廓解
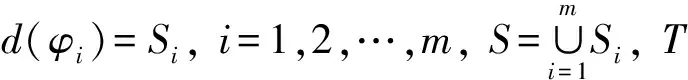
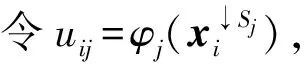
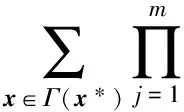
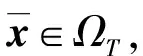
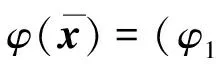
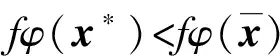


(1.CollegeofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710062,China;
2.CollegeofStatistics,Xi’anUniversityofFinanceandEconomics,Xi’an710100,China)
