ℝ3中一类共线数字集自仿测度的谱性质

高 桂 宝

（1.陕西师范大学 数学与信息科学学院，西安710062；2.运城学院 应用数学系，山西 运城044000）

0 引 言

目前，谱自仿测度问题的研究主要体现在两方面：一方面，在什么条件下μM，D是一个谱测度［1－5］；另一方面，关于μM，D不是谱测度条件的研究［6－7］.文献［8］讨论了扩张整矩阵M和ℤ3中的数字集D分别为M＝pI3，D＝｛0，1，l｝v或者D＝｛0，1｝v所产生自仿测度的谱与非谱性质，其中：p∈ℤ＼｛0，±1｝；v＝｛α，β，γ｝T∈ℝ3，α2＋β2＋γ2≠0.其谱性只与 M，D 有关，本文考虑当数字集的个数超过3时的情形，讨论ℝ3中的（M，D）对，其中M，D 分别为M＝pI3，D＝｛0，1，2，…，q－1｝v，这里：

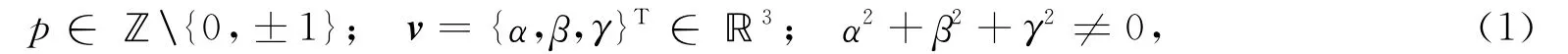
得到了几个μM，D的谱性与非谱性结果.

如果存在一个离散点集Λ⊂ℝn，使得E（Λ）∶＝ ｛e2πi〈λ，x〉：λ∈Λ｝成为L2（μ）的一个正交基，则称一个支撑在ℝn中紧集上的概率测度μ为谱测度，集合Λ称为μ的一个谱.由仿射迭代函数系｛φd（x）＝ M－1（x＋d）｝d∈D迭代产生的不变测度μ∶＝μM，D满足

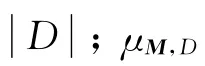
猜测1［9－10］设M∈Mn（ℤ）是扩张整数矩阵，D⊂ℤn是有限集，且0∈D.如果存在S⊂ℤn，0∈S，使得（M－1D，S）是和谐对，则μM，D是一个谱测度.

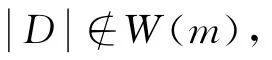
本文结果提供了支持猜测1和猜测2可能成立的理论依据.

1 主要结果

定理1 设扩张矩阵M和数字集D由式（1）给出，q＝4，则：

1）当p∈4ℤ＋｛1，3｝时，L2（μM，D）中至多有4个正交指数函数；

2）当p∈4ℤ时，μM，D是谱测度.

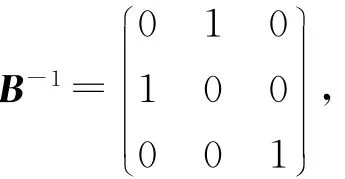
M1＝B－1MB＝M，而μM，D与μM1，D1的谱性质相同.

令

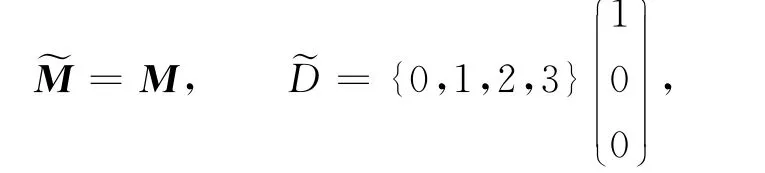
从而μM，D与的谱性质相同.

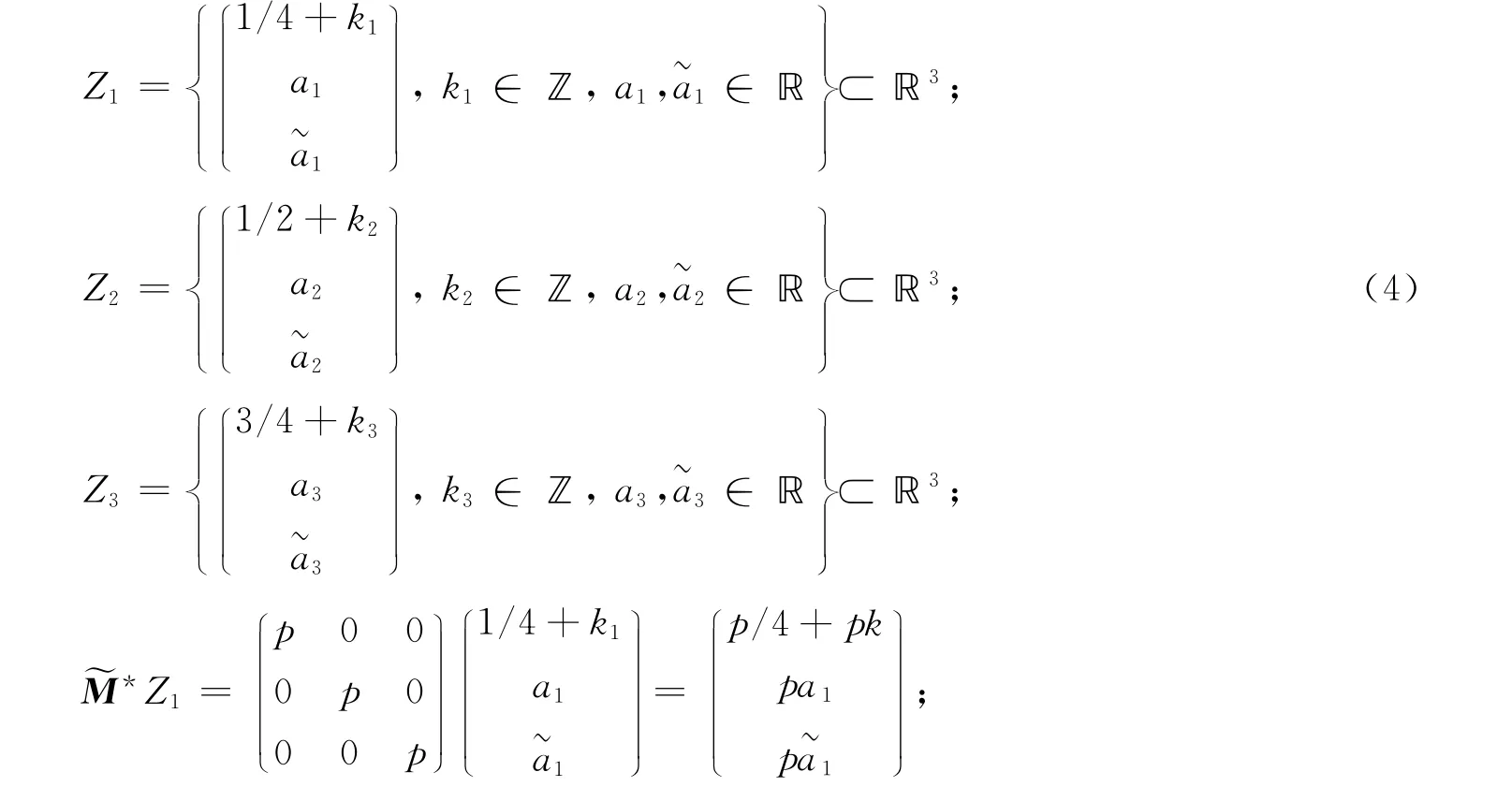
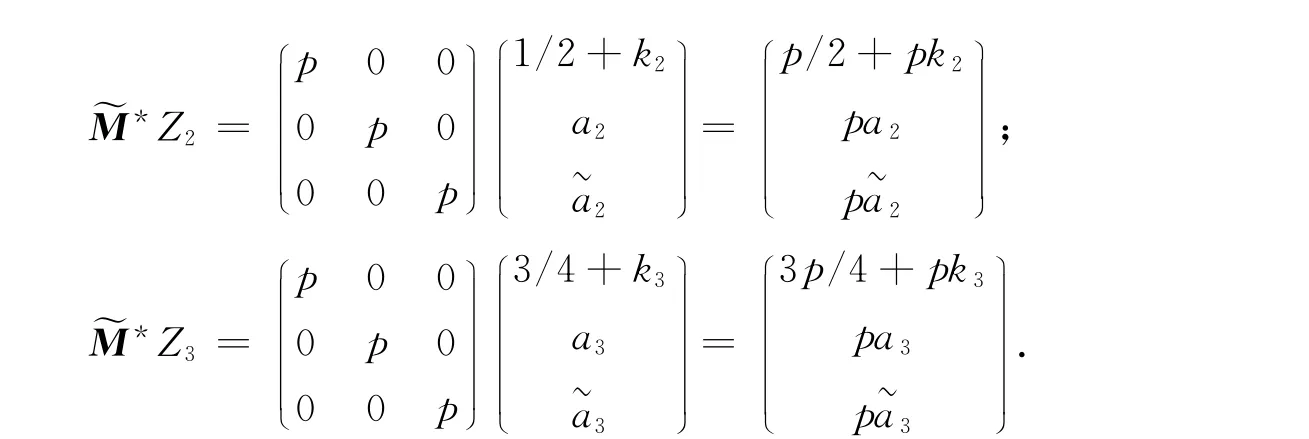
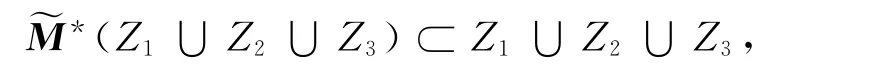
从而

假设λj∈ℝ2（j＝1，2，3，4，5）.使得

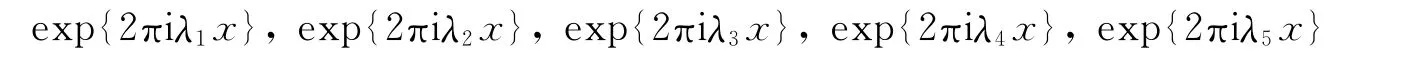
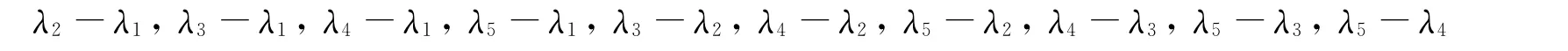
是Z1∪Z2∪Z3中的10个元素，由抽屉原理知，Zi（i＝1，2，3）中有一个集合至少包含前4个元素中的2个元素，而这是不可能的.例如，若λ2－λ1，λ3－λ1∈Z1，则

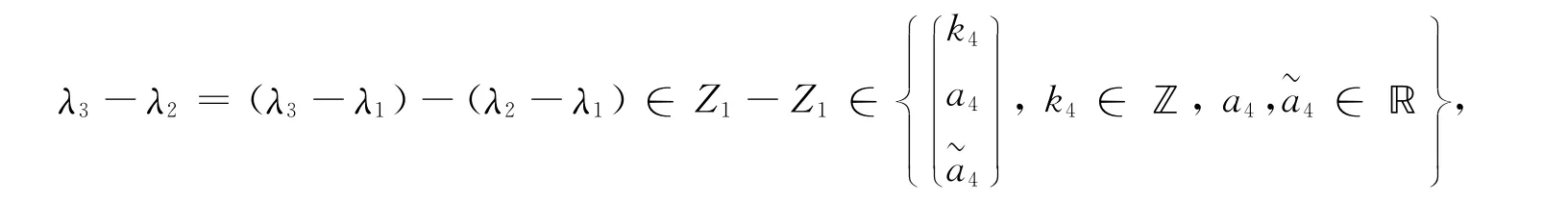
而λ3－λ2∈Z1∪Z2∪Z3与

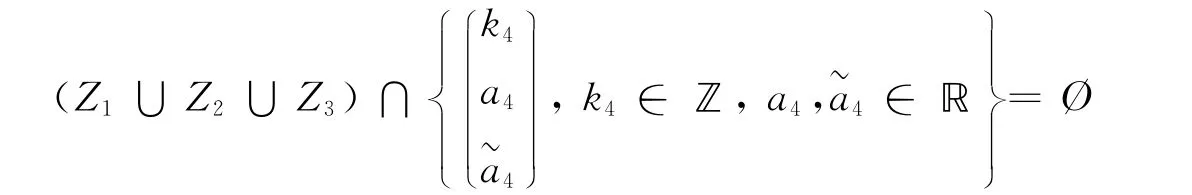
2）由于p∈4ℤ时，

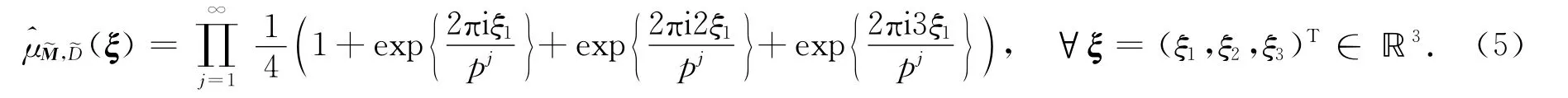
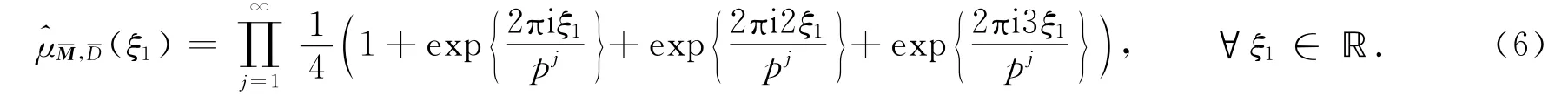
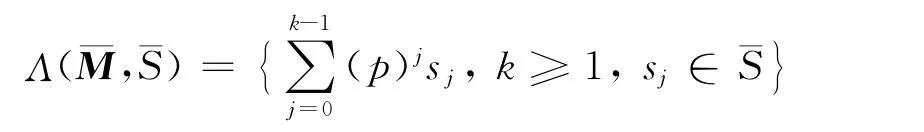
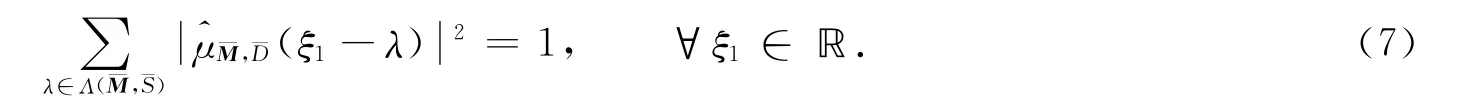
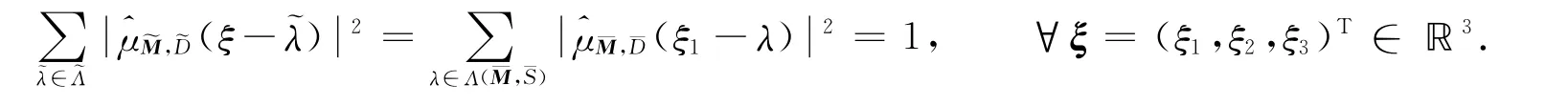
定理1推广到ℝn空间上也成立，有下述推论：

推论1 设扩张矩阵M＝pIn和数字集D由式（1）给出（其中v∈ℝn且非零），q＝4，则：

1）当p∈4ℤ＋｛1，3｝时，L2（μM，D）中至多有4个正交指数函数；

2）当p∈4ℤ时，μM，D是谱测度.

对数字集个数q＞4时的情形有下列定理：

定理2 设扩张矩阵M和数字集D由式（1）给出，q＞4，则下列两个结论成立：

2）L2（μM，D）空间中有无限相互正交的指数函数当且仅当p，q的最大公因子大于1.

证明：记

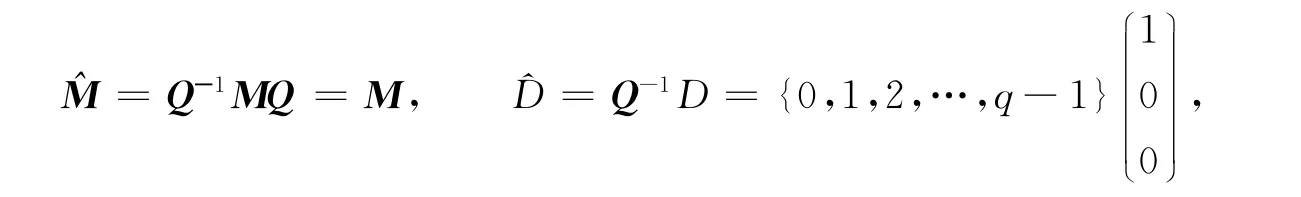
从而μM，D与谱性质相同.

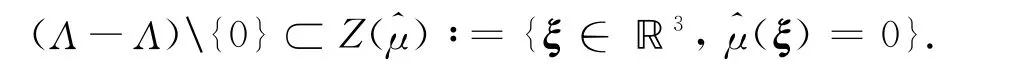
对于μ＝μM，D，由式（2）可得

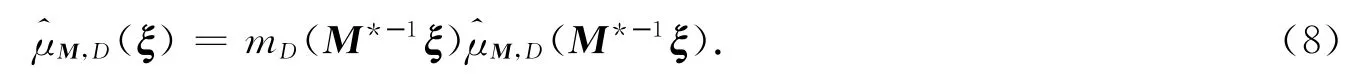
通过迭代有

其中

则

其中ξ＝（ξ1，ξ2，ξ3）T∈ℝ3.

记

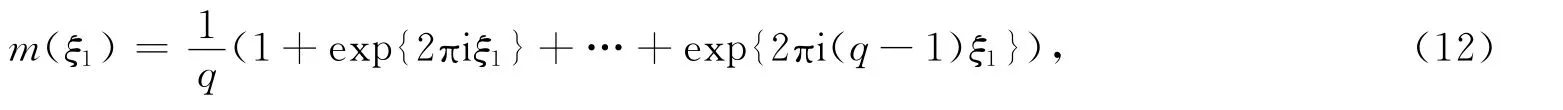
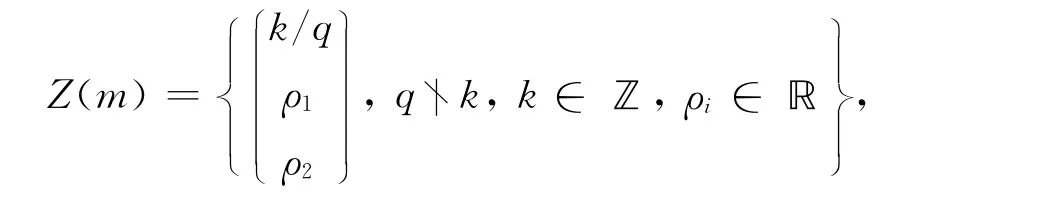
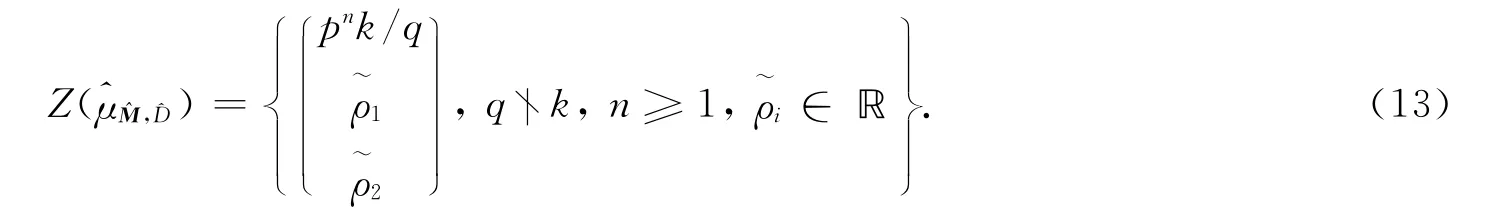
设gcd（q，p）＝d.假设q和p互素，即d＝1.设

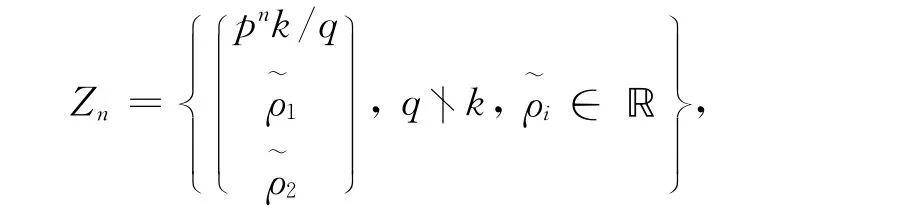
则

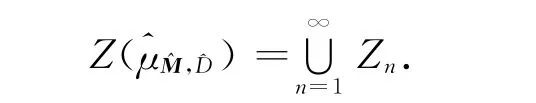
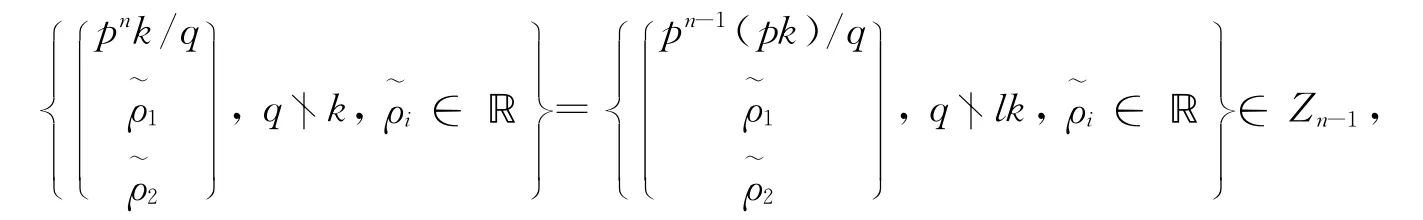
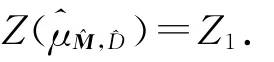
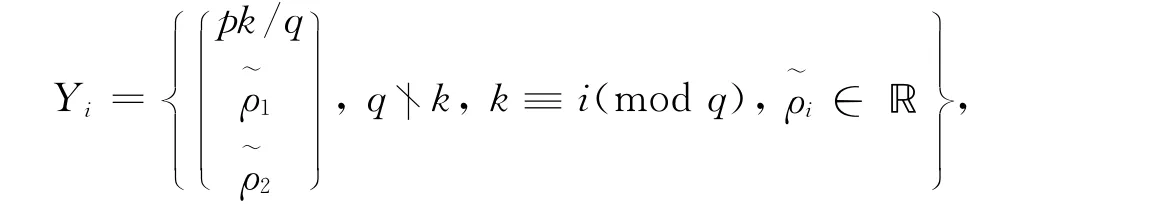
假设d＞1，显然d≤q.

1）先考虑d＝q并且证明其对应的测度是谱测度.记p＝qr并定义

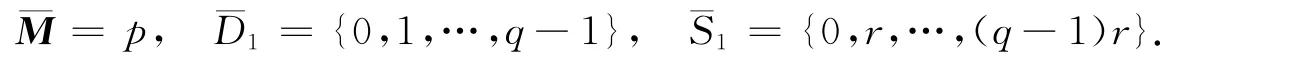
易验证矩阵

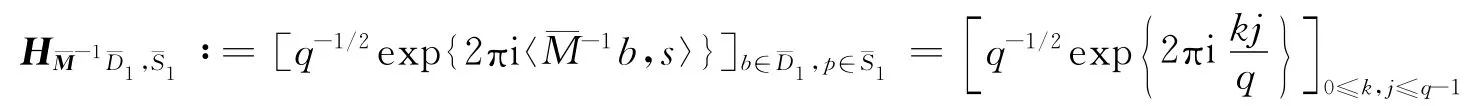
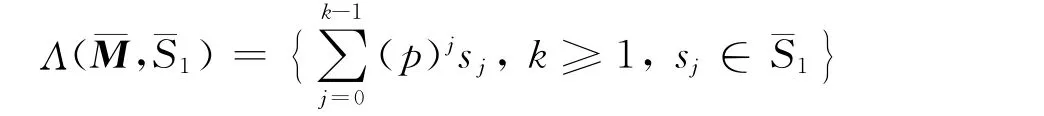
是它的一个谱，等价于下列等式成立：

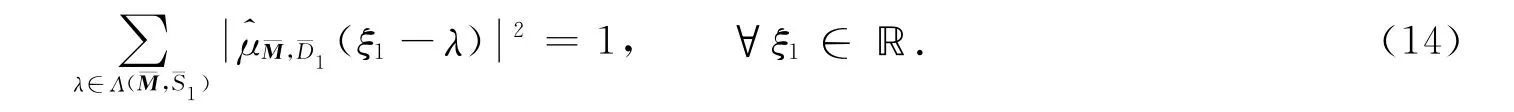
而

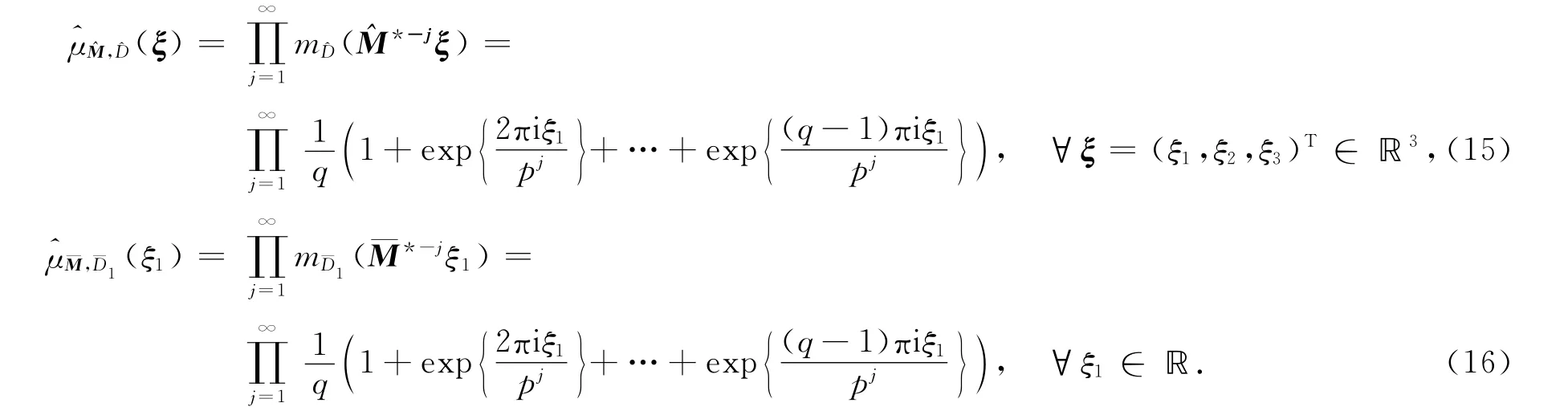
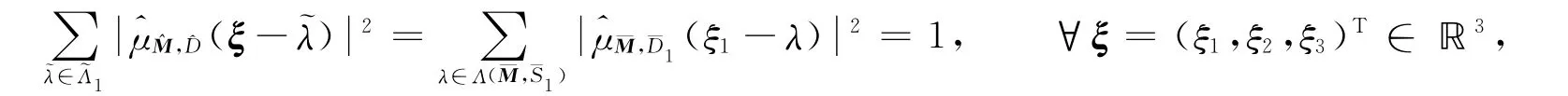
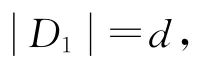
从而

定理2推广到ℝn空间上也成立，有下述推论：

推论2 设扩张矩阵M 和数字集D 分别为M＝pIn，D＝｛0，1，…，q－l｝v，其中p∈ℤ＼｛0，±1｝，In是n阶单位矩阵，v是ℝn中的非零列向量，则：

2）L2（μM，D）空间中有无限相互正交的指数函数当且仅当p，q的最大公因子大于1.

［1］Jorgensen P E T，Pedersen S.Dense Analytic Subspaces in Fractal L2－Spaces［J］.J Anal Math，1998，75（1）：185－228.

［2］Laba I，WANG Yangang.On Spectral Cantor Measures［J］.J Funct Anal，2002，193（2）：409－420.

［3］LI Jianlin，WEN Zhiying.Spectrality of Planar Self－affine Measures with Two－Element Digit Set［J］.Sci China Math，2012，55（3）：593－605.

［4］LI Jianlin.Orthogonal Exponentials on the Generalized Plane Sierpinski Gasket［J］.J Approx Theory，2008，153（2）：161－169.

［5］LI Jianlin.Spectral Self－affine Measures inℝn［J］.Proc Edinburgh Math Soc，2007，50（1）：197－215.

［6］LI Jianlin.Non－spectrality of Planar Self－affine Measures with Three－Elements Digit Set［J］.J Funct Anal，2009，257（2）：537－552.

［7］LI Jianlin.The Cardinality of Certainμ，M，D－Orthogonal Exponentials［J］.J Math Anal Appl，2010，362（2）：514－522.

［8］高桂宝.ℝ3中共线数字集自仿测度的谱性质 ［J］.吉林大学学报：理学版，2014，52（2）：190－194.（GAO Guibao.Spectrality of Self－affine Measures with Collinear Digit Set onℝ3［J］.Journal of Jilin University：Science Edition，2014，52（2）：190－194.）

［9］Dutkay D E，Jorgensen P E T.Fourier Frequencies in Affine Iterated Function Systems［J］.J Funct Anal，2007，247（1）：110－137.

［10］Dutkay D E，Jorgensen P E T.Analysis of Orthogonality and of Orbits in Affine Iterated Function Systems［J］.Math Z，2007，256（4）：801－823.

［11］Dutkay D E，Jorgensen P E T.Probability and Fourier Duality for Affine Iterated Function Systems［J］.Acta Appl Math，2009，107（1／2／3）：293－311.