基于稳定阈值的吸引子传播算法

王丽敏, 王依章, 韩旭明, 黄 娜

(1.吉林财经大学 管理科学与信息工程学院, 长春 130117；2.长春工业大学 计算机科学与工程学院, 长春 130012；3.上海财经大学 信息管理与工程学院, 上海 200433)

基于稳定阈值的吸引子传播算法

王丽敏1, 王依章1, 韩旭明2, 黄 娜3

(1.吉林财经大学 管理科学与信息工程学院, 长春 130117；
2.长春工业大学 计算机科学与工程学院, 长春 130012；
3.上海财经大学 信息管理与工程学院, 上海 200433)

针对传统吸引子传播算法(AP)聚类性能受偏向参数影响较大的问题, 提出一种改进的吸引子传播算法, 即基于稳定阈值的吸引子传播聚类算法(STAP).该算法通过稳定阈值, 衡量获得真实类数时的收敛状态, 然后捕捉该状态下的偏向参数； 为加快算法的收敛速度, 采用S型函数作为收敛因子调节阻尼系数.仿真模拟实验结果表明, 与传统吸引子传播聚类算法相比, 基于稳定阈值的吸引子传播聚类算法聚类精度更高, 收敛速度更快.

吸引子传播算法； 稳定阈值； 收敛因子

吸引子传播算法(affinity propagation, AP)是一种新聚类算法.目前, 该算法已成功应用于图像分割[1-3]、图像检索[4]、基因识别[5]、文本聚类[6]和最优航空路线确定[7]等领域.目前, 对该算法已有多种改进方法, 如Sakellariou等[8]提出了将多重假设检验和吸引子传播算法相结合, 对基因表达数据进行分类的方法； Qasim等[9]提出了将吸引子传播算法与文本概念图半自动生成技术相结合的方法； 于吉红等[10]提出了用空间向量模型计算特征相似度, 并已应用于舰船三维模型进行视点空间均匀投影； 张震等[11]提出了将吸引子传播算法与半监督流量分类相结合的方法, 即STI-AP算法.针对上述算法, 本文提出一种稳定阈值函数优化偏向参数, 提高吸引子传播算法对类空间搜索准确度的方法——基于稳定阈值的吸引子传播聚类算法(STAP), 该方法采用Sigmoid函数作为收敛因子的加速策略, 以提高算法对高维大数据的处理能力, 加快算法的收敛速度.

1 吸引子传播聚类算法

吸引子传播聚类算法将数据集的所有样本点均视为候选类代表点, 利用数据点间的相似度构造相似度关系矩阵S[12-13], 其中相似度是两点间距离的相反数[14], 公式如下：

s(i,k)=-‖xi-xk‖.

（1）

在吸引子传播聚类算法中, 初始假设每个样本成为类代表点的可能性相同[15], 即设定所有s(k,k)为相同值P,P值是相似度矩阵所有值的中位数[16].该算法引入两个重要信息参数共同决定各样本的类代表点, 分别是归属度矩阵A=(a(i,k))m×n和吸引度矩阵R=(r(i,k))m×n, 算法迭代过程是两种信息量迭代更新的过程, 其中:a(i,k)是样本Xk发送给样本Xi的信息量, 描述i点选择k点作为聚类中心的适合程度;r(i,k)是样本Xi发送给样本Xk的信息量, 描述k点适合作为数据点i的聚类中心的适合程度[17].算法结束时, 通过公式

计算归属度a(i,k)、吸引度r(i,k)及二者之和, 获得每个样本的类代表点[18-19].

在吸引子传播聚类算法中, 引入阻尼因子增强算法迭代的稳定性[20], 公式如下:

其中,t为当前迭代次数.本文设当类代表点在连续10次迭代过程中不发生变化或达到最大迭代次数时, 算法结束.

2 STAP算法描述

2.1偏向参数优化技术

表1列出了偏向参数在不同倍数下的各项试验参数.由表1可见, 偏向参数P值对聚类精度、聚类类数和迭代速度均有较大影响.通过选取合适的偏向参数, 能获得标准数据集的最佳聚类类数, 提高聚类性能.本文提出的基于稳定阈值的吸引子传播聚类算法能有效解决偏向参数的优化问题, 使类空间的搜索精度更准确.图1为在不同偏向参数下Ionosphere数据集的聚类类数.由图1可见, Ionosphere数据集的聚类类数随偏向参数的增大出现3个阶段的变化: 第一阶段为收敛阶段, 该阶段聚类结果较好, 较少发生重复现象, 算法收敛速度较快; 第二阶段为稳定阶段, 该阶段获得该数据集的最优聚类类数, 同时聚类精度较高； 第三阶段是震荡阶段, 算法发生震荡, 此时该算法所得到的聚类结果失真.大量数据集实验表明, 使用吸引子传播聚类算法进行仿真模拟聚类均有上述3个阶段的变化.

基于稳定阈值的吸引子传播聚类算法是一种偏向参数优化技术, 即用稳定阈值衡量算法的稳定状态并通过数学建模量化该状态.稳定阈值描述聚类结果的重复度, 重复度越大, 算法迭代越稳定, 聚类类数越接近真实类数.此时, 在类空间对应的偏向参数下, 聚类性能更优.数据集的样本数和维度对吸引子传播聚类算法的聚类结果影响较大, 因此, 本文提出一种关于样本数与维度比的线性函数作为稳定阈值的极限值:

其中： SN表示样本数; dim表示维度.

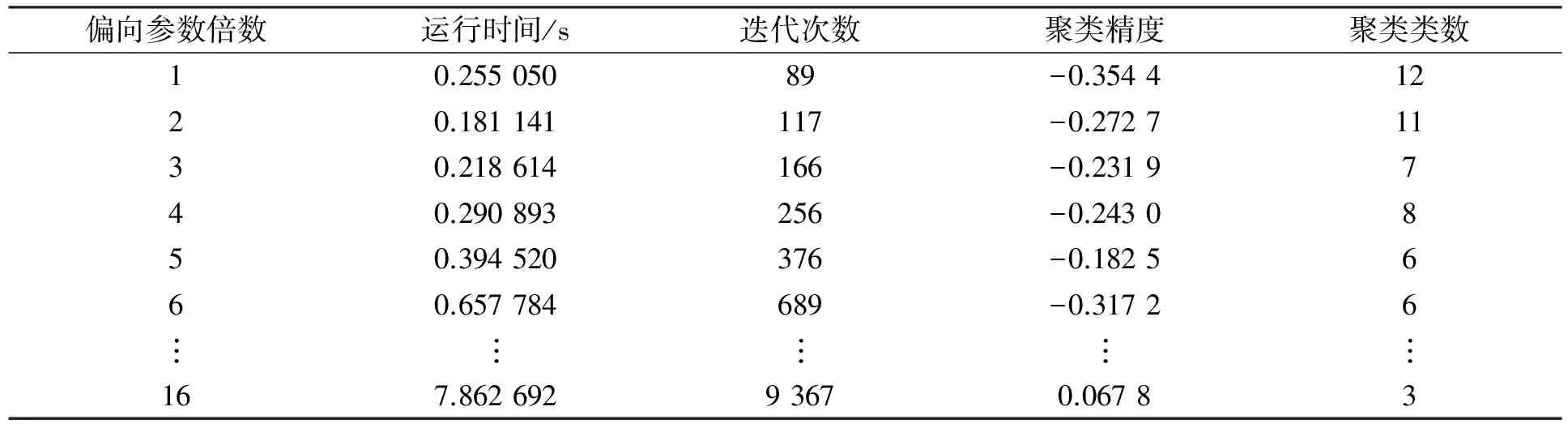
表1 不同偏向参数下AP聚类算法对Wine数据集的聚类参数Table 1 Clustering parameters of Wine data set by AP clustering algorithm at different P values

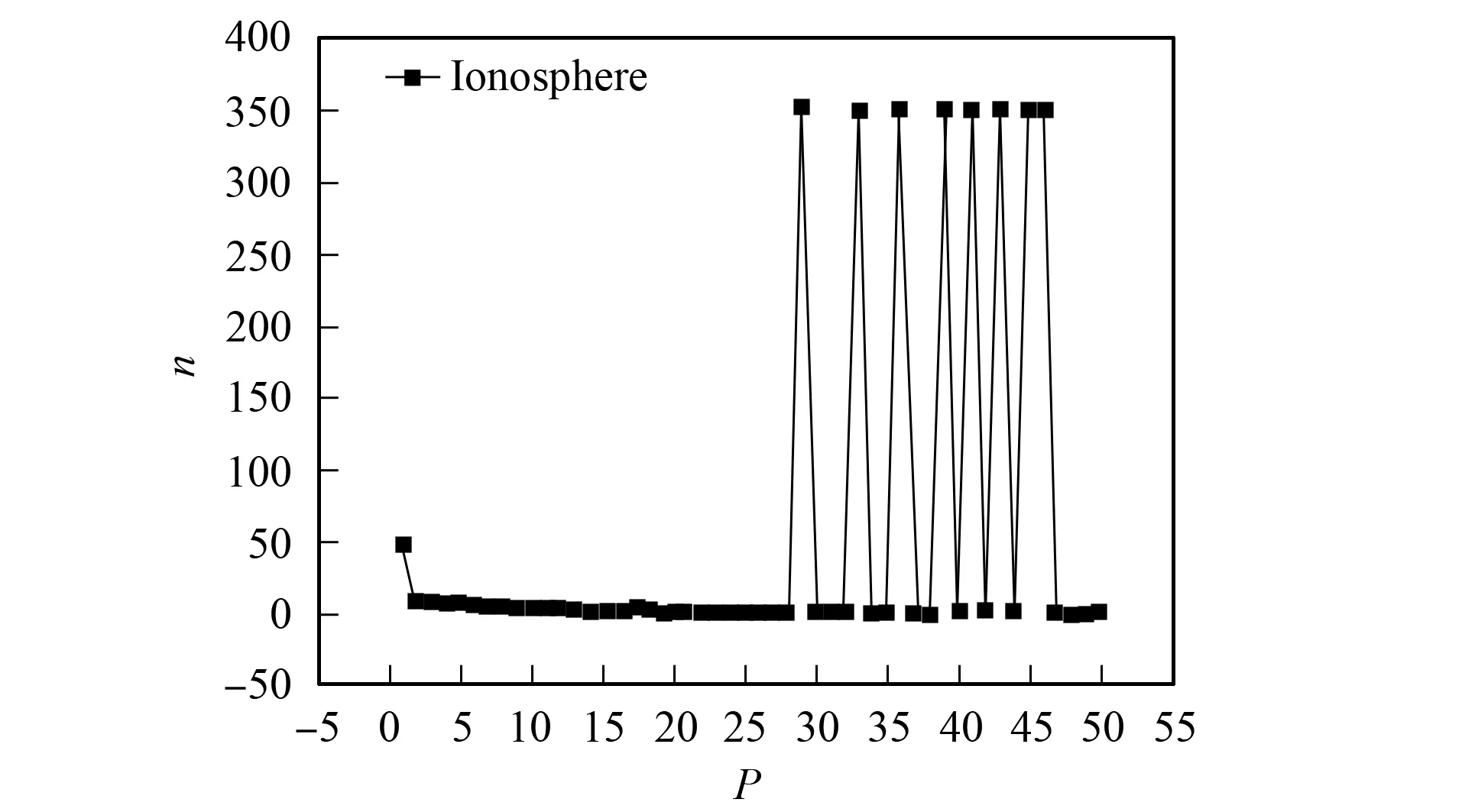
图1 在不同偏向参数P下Ionosphere数据集的聚类类数Fig.1 Class number of Ionosphere at different P values

稳定阈值的大小主要由样本数和维度决定.样本数越大, 维度越小, 动态搜索程度越大, 这符合吸引子传播聚类算法的聚类原理.n与样本数和维度的比值成正比, 通过基于稳定阈值吸引子传播聚类算法的遍历搜索n, 使算法与数据集的拟合度最高.

基于稳定阈值吸引子传播聚类算法提出基于稳定因子、震荡因子和弱稳定因子的线性函数作为稳定阈值的度量函数.稳定因子为聚类重复度, 震荡因子为聚类震荡度, 弱稳定因子数为聚类结果顺序递减度.引入弱稳定因子能更准确地捕捉震荡度少的数据集类空间的稳定状态.因此稳定阈值为

其中： SF为稳定因子; CF为震荡因子; WSF为弱稳定因子.

2.2S型收敛因子加速技术

针对传统吸引子传播聚类算法在对大数据和高维数据聚类时存在处理速度较慢的问题, 本文提出一种基于S型收敛因子的加速技术.在吸引子传播聚类算法中, 阻尼系数越大, 收敛速度越慢, 合适的阻尼系数将会减少算法运行时间.以Sigmoid函数为筛选器寻找最优收敛因子, 将其引入该算法提高算法的迭代速度:

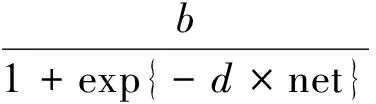
（9）

基于稳定阈值的吸引子传播聚类算法如下：

1) 输入相似性矩阵S(i,j)；

2) 优化搜索偏向参数, 步长为1, 初始偏向参数是相似性矩阵S(i,j)的中位数；

3) 初始化稳定阈值ST及其相关参数, 迭代更新ST,SF,CF,WSF；

4) 更新矩阵R和矩阵A;

5) 更新吸引度和归属度矩阵:

r(i,k)(t+1)=f(net)·λ·r(i,k)(t)+(1-λ)·r(i,k)(t-1),

a(i,k)(t+1)=f(net)·λ·a(i,k)(t)+(1-λ)·a(i,k)(t-1);

6) 更新稳定阈值ST, 达到极限值, 算法结束.

3 仿真模拟实验与分析

仿真模拟实验环境为Pentium G645 2.9 GHz CPU, 4 Gb内存.实验参数是阻尼系数λ=0.5,t=10, 算法评价指标选用Silhouette指标.为了有效验证本文改进算法的可行性与有效性, 选取高维和低维两类数据集作为仿真模拟实验的数据样本, 实验数据列于表2.

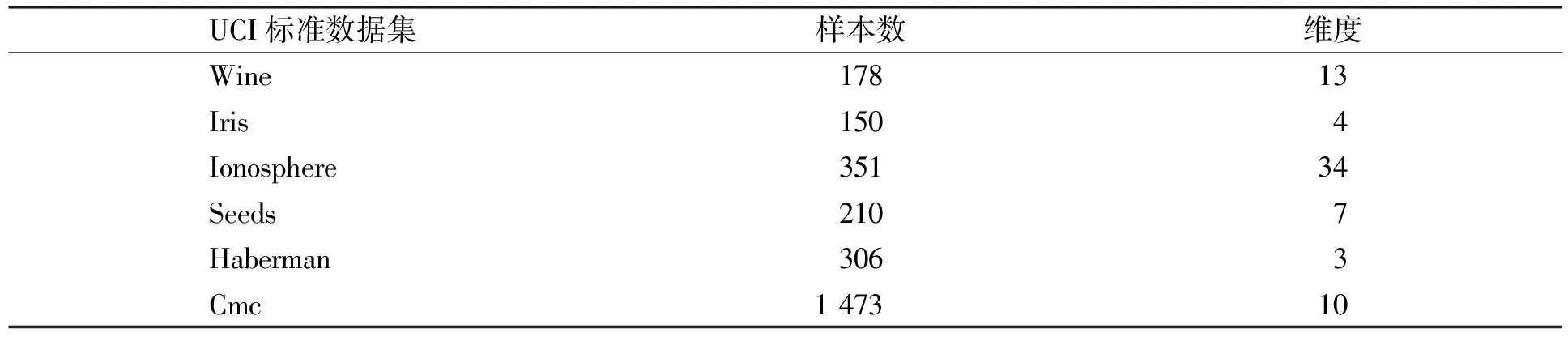
表2 实验数据集参数Table 2 Characteristic parameters of experimental data sets

用本文提出的基于稳定阈值吸引子传播聚类算法进行仿真模拟实验, 实验结果列于表3.低维数据中样本数少的Wine,Iris,Seeds,Harberman数据集, 其算法运行时间差异较小, 而高维Ionosphere数据集算法运行时间却减少了73.3%； 多样本数Cmc数据集算法运行时间减少了11%.上述实验结果表明： 样本数和维度越大, 算法运行时间越少, 因此本文提出的改进算法能有效提高高维大数据聚类效率.图2和图3是采用人工数据集, 分别利用传统AP算法及本文提出的改进AP算法进行仿真模拟实验获得的聚类结果.人工数据集由MATLAB自动生成二项分布随机数据.对于同一个人工数据集, 采用传统AP聚类算法获得的聚类结果为6类, 而本文算法获得的聚类结果为2类, 改进的AP聚类结果更符合数据的实际空间分布特征, 识别率为100%.因此, 改进的AP聚类算法具有更优的聚类性能.

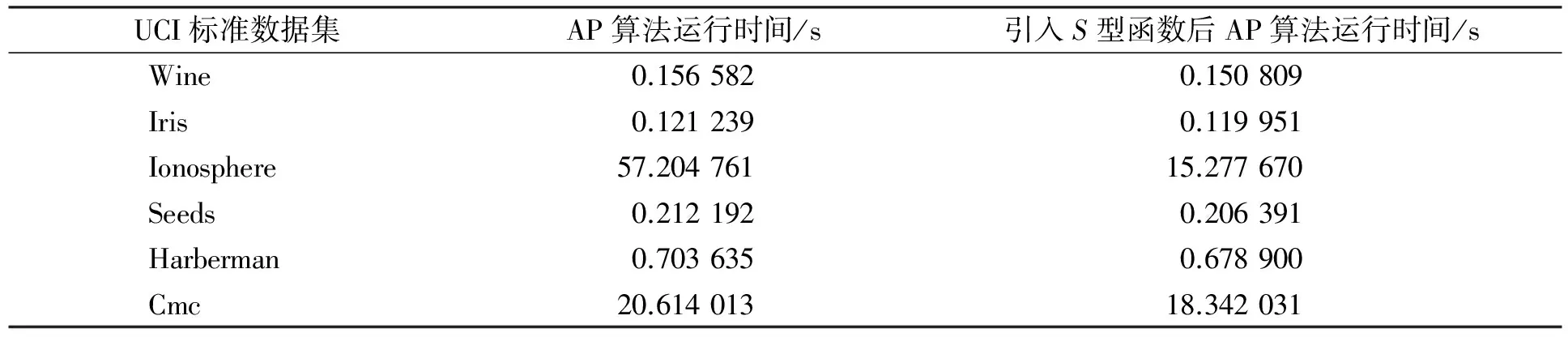
表3 AP算法和改进AP算法运行时间的比较Table 3 Comparison of time by AP and improved AP algorithms

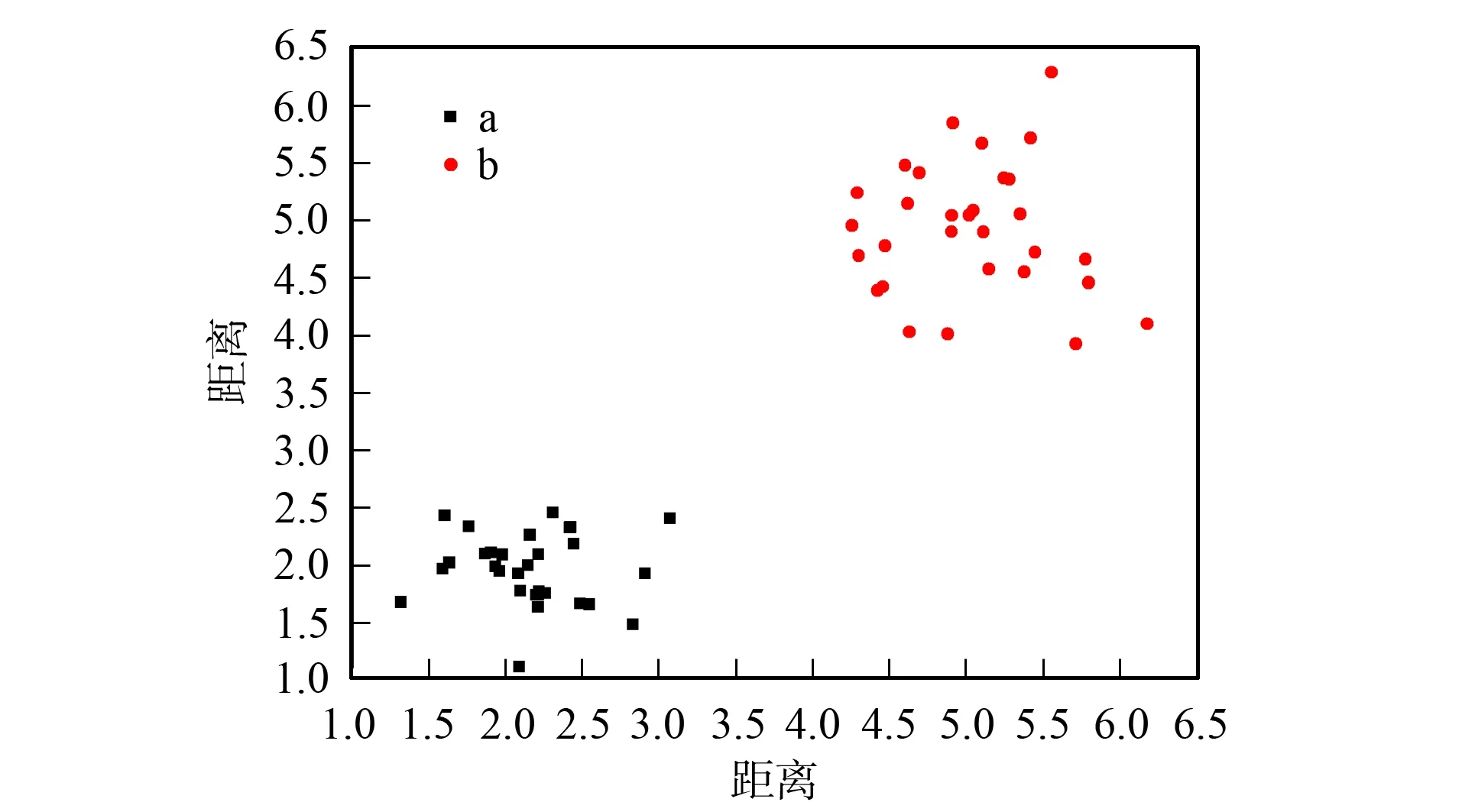
图2 改进的AP聚类算法聚类结果Fig.2 Clustering result of improved AP clustering algorithm

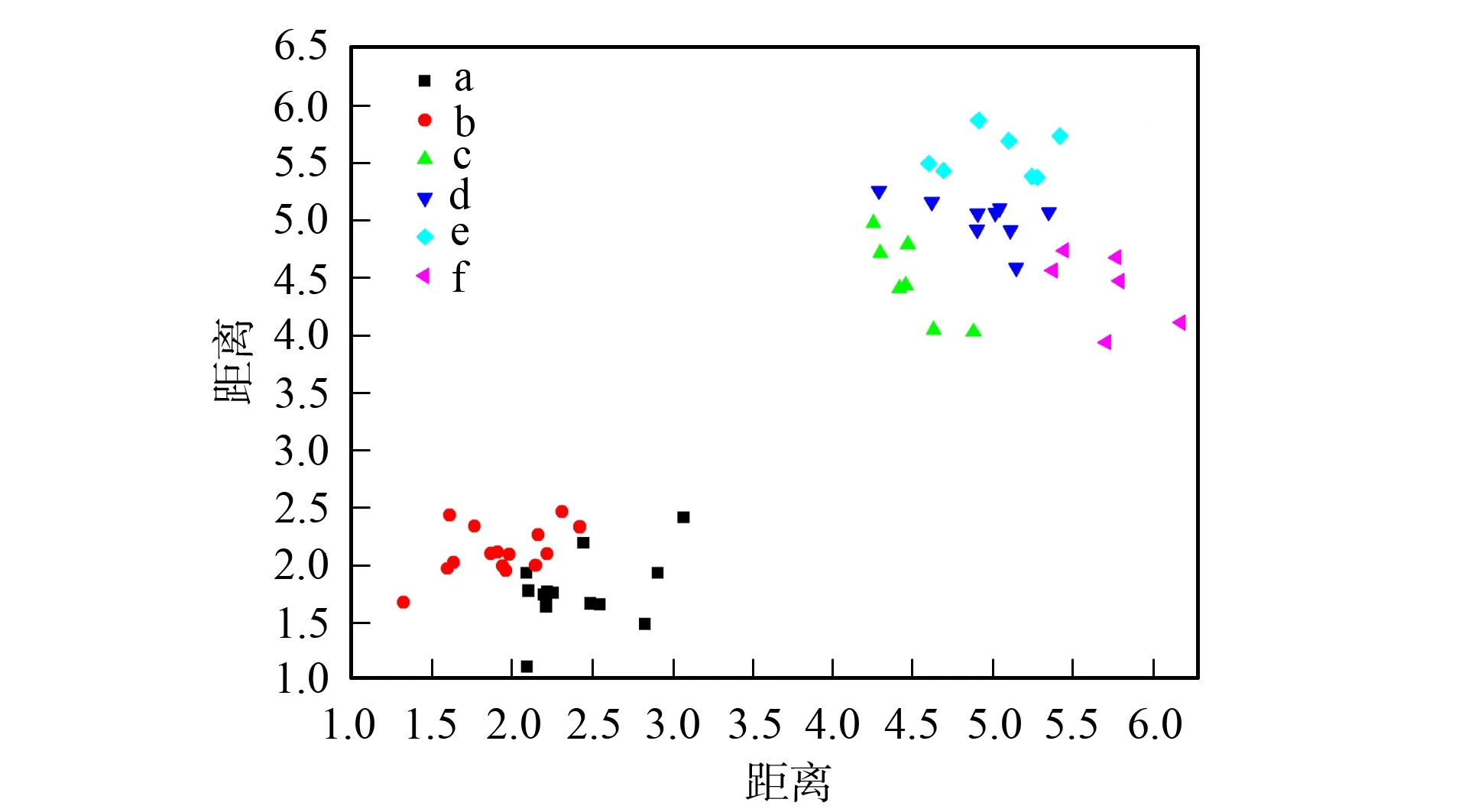
图3 传统AP聚类算法聚类结果Fig.3 Clustering result of traditional AP clustering algorithm

AP算法和改进AP算法对标准数据集的聚类结果比较列于表4.由表4可见, 与传统AP算法相比, 改进AP算法 Silhouette值明显提高, 在Wine,Iris等数据集中, 实现了对偏向参数的优化, 聚类类数均能达到真实类数, 大幅度提高了传统AP算法的聚类性能.

表4 AP算法和改进AP聚类算法实验结果比较Table 4 Comparison of experimental results between AP and improved AP clustering algorithms

综上所述, 传统吸引子传播聚类算法具有无法获取先验偏向参数, 高维大数据收敛速度慢的弊端.基于稳定阈值的吸引子传播聚类算法通过稳定阈值的方法, 在类空间捕捉稳定状态和该状态下的偏向参数, 达到了优化偏向参数的目的.将Sigmoid函数引入到该算法中作为收敛因子, 可加快算法的单次循环收敛速度.偏向参数优化策略和算法加速方法的结合克服了传统AP算法存在的弊端.

[1]Napoleon D, Praneesh M, Subramanian M S.Manhattan Distance Based Affinity Propagation Technique for Clustering in Remote Sensing Images [J].International Journal, 2012, 2(3): 327-329.

[2]许晓丽, 卢志茂, 张格森, 等.改进近邻传播聚类的彩色图像分割 [J].计算机辅助设计与图形学学报, 2012, 24(4)： 514-519.(XU Xiaoli, LU Zhimao, ZHANG Gesen, et al.Color Image Segmentation Based on Improved Affinity Propagation Clustering [J].Journal of Computer-Aided Design & Computer Graphics, 2012, 24(4): 514-519.)

[3]杨传慧, 吉根林, 章志刚.基于分块加权颜色直方图的图像聚类算法研究 [J].南京师范大学学报: 工程技术版, 2013, 13(1)： 40-44.(YANG Chuanhui, JI Genlin, ZHANG Zhigang.Research on Image Clustering Algorithm Based on Block Weighted Color Histogram [J].Journal of Nanjing Normal University: Engineering and Technology Edition, 2013, 13(1): 40-44.)

[4]孙永宣, 谢昭, 高隽.图像奇异性检测的核分类新方法 [J].光学学报, 2013, 33(10)： 1015001.(SUN Yongxuan, XIE Zhao, GAO Jun.A Novel Kernel Classification Method via Image Novelty Detection [J].Acta Optica Sinica, 2013, 33(10): 1015001.)

[5]汤健, 管云雁, 刘文广, 等.马氏珠母贝家系遗传结构的微卫星分析 [J].海洋科学, 2013, 37(8)： 35-41.(TANG Jian, GUAN Yunyan, LIU Wenguang, et al.Microsatellite DNA Analysis of Genetic Structures about 9 Families of Pinctada Fucata [J].Marine Sciences, 2013, 37(8): 35-41.)

[6]文翰, 肖南峰.基于强类别特征近邻传播的半监督文本聚类 [J].模式识别与人工智能, 2013, 27(7): 646-654.(WEN Han, XIAO Nanfeng.A Semi-supervised Text Clustering Based on Strong Classification Features Affinity Progation [J].PR & AI, 2013, 27(7): 646-654.)[7]郑志敏, 徐青.基于仿射传播算法的城市航空便利性分析 [J].硅谷, 2013(9)： 72-74.(ZHENG Zhimin, XU Qing.Analysis of City Aviation Convenience Based on Affinity Propagation [J].Silicon Valley, 2013(9): 72-74.)

[8]Sakellariou A, Sanoudou D, Spyrou G.Combining Multiple Hypothesis Testing and Affinity Propagation Clustering Leadsto Accurate, Robust and Sample Size Independent Classification on Gene Expression Data [J].BMC Bioinformatics, 2012, 13: 270.

[9]Qasim I, Jeong J W, Heu J U, et al.Concept Map Construction from Text Documents Using Affinity Propagation [J].Journal of Information Science, 2013, 39(6): 719-736.

[10]于吉红, 白晓明, 吕俊伟.改进相似度的仿射传播聚类算法 [J].小型微型计算机系统, 2013, 34(3)： 602-605.(YU Jihong, BAI Xiaoming, LÜ Junwei.Affinity Propagation Clustering Based on New Similarity [J].Journal of Chinese Computer Systems, 2013, 34(3): 602-605.)

[11]张震, 汪斌强, 李向涛, 等.基于近邻传播学习的半监督流量分类方法 [J].自动化学报, 2013, 39(7)： 1100-1109.(ZHANG Zhen, WANG Binqiang, LI Xiangtao, et al.Semi-supervised Traffic Identification Based on Affinity Propagation [J].Acta Automatica Sinica, 2013, 39(7): 1100-1109.)

[12]Sattar F, Driessen P F.Non-stationary Signals Separation Using STFT and Affinity Propagation Clustering Algorithm [C]//2013 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing.Victona, BC: IEEE, 2013: 389-394.

[13]Foster B, Bagci U, Luna B, et al.Robust Segmentation and Accurate Target Definition for Positron Emission Tomography Images Using Affinity Propagation [C]//2013 IEEE 10th International Symposium on Biomedical Imaging (ISBI).San Francisco: IEEE, 2013: 1461-1464.

[14]张震, 汪斌强, 伊鹏, 等.一种分层组合的半监督近邻传播聚类算法 [J].电子与信息学报, 2013, 35(3)： 645-651.(ZHANG Zhen, WANG Binqiang, YI Peng, et al.Semi-supervised Affinity Propagation Clustering Algorithm Based on Stratified Combination [J].Journal of Electronics & Information Technology, 2013, 35(3): 645-651.)

[15]王文帅, 陈刚.基于半监督近邻传播的数据流聚类算法 [J].计算机工程与应用, 2013, 49(8)： 6-8.(WANG Wenshuai, CHEN Gang.Data Stream Clustering Algorithm Based on Semi-supervised Affinity Propagation [J].Computer Engineering and Applications, 2013, 49(8): 6-8.)

[17]Vannieuwenhoven N, Vandebril R, Meerbergen K.A New Truncation Strategy for the Higher-Order Singular Value Decomposition [J].SIAM Journal on Scientific Computing, 2012, 34(2): A1027-A1052.

[18]Makbol N M, Khoo B E.Robust Blind Image Watermarking Scheme Based on Redundant Discrete Wavelet Transform and Singular Value Decomposition [J].International Journal of Electronics and Communications, 2013, 67(2): 102-112.

[19]Hassanbadi B, Shea C, Zhang L, et al.Clustering in Vehicular and Hoc Networks Using Affinity Propagation [J].Ad Hoc Networks, 2014, 13: 535-548.

[20]Quera V, Beltran F S, Givoni I E, et al.Determing Shoal Membership Using Affinity Propagation [J].Behavioural Brain Research, 2013, 241: 38-49.

StabilityThreshold-BasedAffinityPropagationAlgorithm

WANG Limin1, WANG Yizhang1, HAN Xuming2, HUANG Na3
(1.SchoolofManagementScienceandInformationEngineering,JilinUniversityofFinanceandEconomics,
Changchun130117,China; 2.SchoolofComputerScienceandEngineering,ChangchunUniversityofTechnology,Changchun130012,China; 3.SchoolofInformationManagementandEngineering,
ShanghaiUniversityofFinanceandEconomics,Shanghai200433,China)

In view of the performance of traditional affinity propagation algorithm greatly influenced by parameterP, a novel affinity propagation algorithm based on stability threshold was proposed.The improved algorithm can obtain the convergence of the real class number by stabilizing threshold, and then gain the corresponding parameterP.In order to improve the convergence speed,Sfunction as convergence factor was applied to adjust damp parameter.In addition, it was successfully applied to the field of financial evaluation of listed companies.Simulation experimental results show that the improved clustering algorithm could obtain better precision and quicker convergence, and is obviously better than traditional affinity propagation clustering algorithm.

affinity propagation algorithm; stability threshold; convergence factor

2014-05-13.

王丽敏(1975—), 女, 汉族, 博士, 教授, 从事机器学习、数据挖掘和金融工程的研究, E-mail: wlm_new@163.com.通信作者： 韩旭明(1971—), 男, 汉族, 博士, 副教授, 从事机器学习和数据挖掘的研究, E-mail: hanxvming@163.com.

国家自然科学基金(批准号： 61202306; 61472049; 61402193)、教育部规划项目(批准号： 13YJAZH130)、吉林省科技厅项目(批准号： 20100507; 201215119; 20130522177JH; 20130101072JC)、吉林省教育厅重点规划项目(批准号： 2012185; 2012189)、吉林省高校新世纪优秀人才支持计划项目(批准号： 2014159)和吉林省社会科学基金(批准号： 2014B166).

TP301

A

1671-5489(2014)06-1249-06

10.13413/j.cnki.jdxblxb.2014.06.27

韩 啸)